透空圆柱体波浪散射及波浪辐射特性分析

乔卫亮， 马来好， 韩晓双， 陈海泉， 孙玉清

(大连海事大学 轮机工程学院，辽宁 大连 116026)

透空结构以其显著的减波、消波特性，在海洋工程领域获得了越来越多的重视。英国的Ekofisk圆柱形海洋结构物[1]以及法国Trfalgar海上风电场[2]均采用了透空薄壁柱体的减波设计。Wang[3]对固定式同心透空圆柱体的波浪载荷特性，建立了解析分析模型，在此基础上 Williams等[4]对中间夹有一段透空薄壁的圆柱体开展了半解析工作，分析了其水动力性能。岳景云等[5]采用复合边界元素法论证了结构物外壁采用透水结构可大幅降低cosine-type同心圆柱体周围的绕射波动，Sarkar等[6]对外层透空结构的围护效果进行了分析，Wang等[7]针对该问题给出了解析计算模型。Ning等[8]通过数值计算模型的搭建以及物理模型实验的实施分析了上部带有透空结构的浮式圆柱体结构的垂荡运动特性。liu等[9]对多层透空薄壁的围护效能进行了数值分析，Chen等[10]用零场积分方程对多个固定式透空圆柱周围的波高分布及波浪载荷进行了半解析分析，Sarkar等[11]在Bhatta[12]对浮式圆柱体水动力性能解析解的基础上，通过推导解析计算模型，分析了浸没式圆柱形透空薄壁对海洋平台的围护效果，后来，Mackay等[13]对固定和浮式透空圆柱体进行了实验分析和数值求解。由于波浪能量大多集中于自由水面附近，目前透空薄壁在自由水面附近的应用研究成果较多[14]，对正下方带有透空薄壁的圆柱形结构物的关注度明显不够，透空薄壁在改善浮式结构物波浪水动力特性方面的潜能有待于进一步开展研究。为了克服以上研究的不足之处，本文以正下方带有圆柱形透空薄壁的浮式结构物为研究对象，基于porous-wavemaker理论[15]和势流理论，针对该结构物的波浪散射和辐射特性，构建解析计算模型，并将结果与现有数值计算结果进行对比分析，基于此，分析透空系数对波浪散射和辐射特性的影响机理。

1 构建理论计算模型

如图1所示，一列波高为H，频率为ω，波长为λ的规则波通过一个半径为a的透空圆柱体，圆柱体浸入水中的非透水高度为h1，透水部分的高度为h2-h1，水深为h0，以静水面与圆柱体轴线的交点为原点，建立柱坐标系。为便于与已有研究成果[4,12]进行对比分析，本文分析辐射特性时，假设浮体系统在三自由度内做微幅振荡运动。

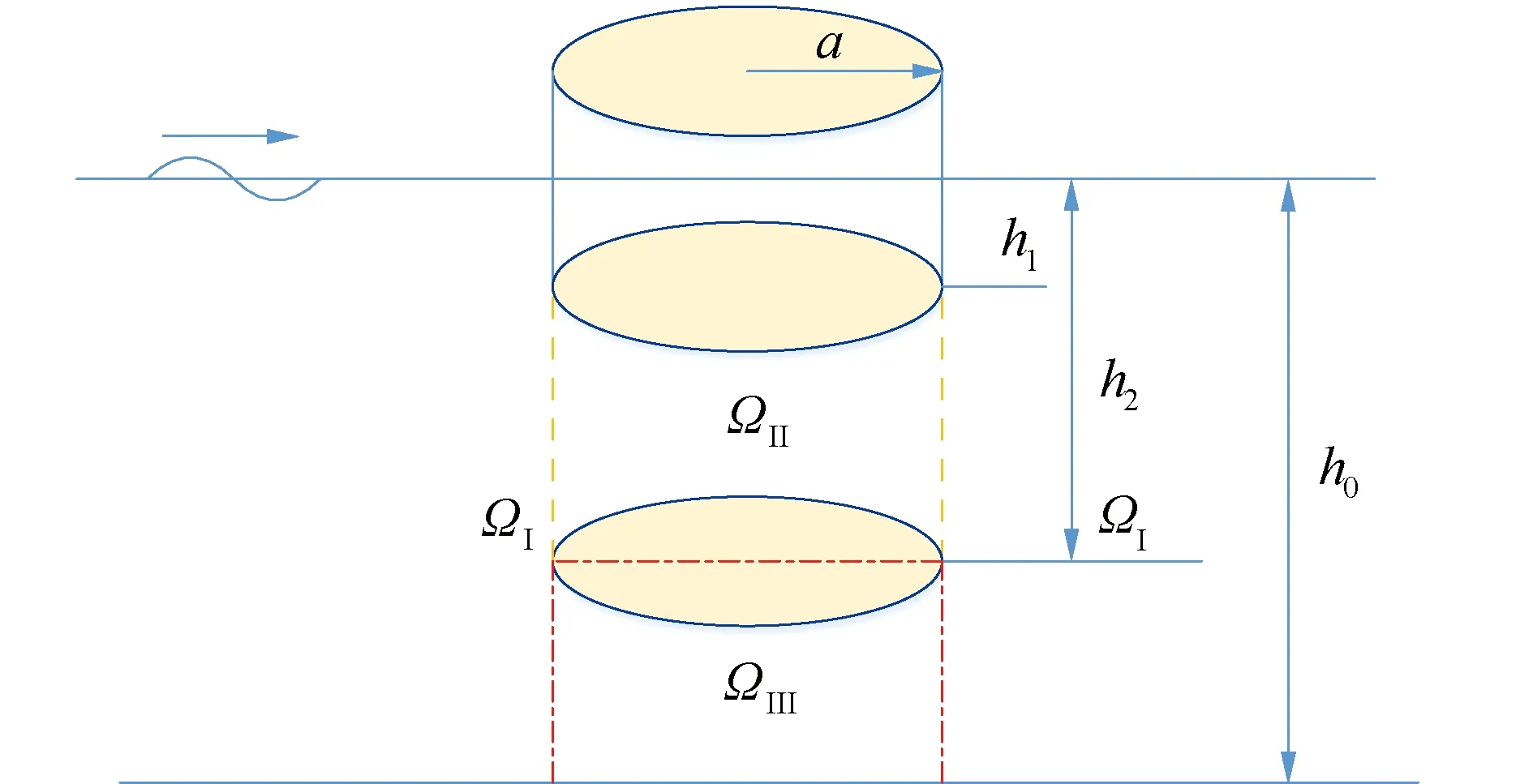
图1 透空柱体与波浪的相互作用示意

假设流体不可压缩且无粘性，浮体固定不动，如图1所示，流体区域分为3部分整个流场分为流域ΩI和ΩII，其范围为：

(1)

根据上述对该问题的描述，可以基于流体势函数的求解对透空柱体与波浪的相互作用进行分析。取Φj(j=1,2,3)分别表示流体区域ΩI、ΩII、ΩIII的流体势函数，在柱坐标下可将其表示为：

Φj(r,θ,z,t)=Re[φj(r,θ,z)e-iωt]

(2)

式中φj(r,θ,z)表示流体区域内势函数的空间表达式部分，在整个流场范围内，速度势函数均满足拉普拉斯方程，在本论文所设定的柱坐标情形下，拉普拉斯方程可以转化为[4]：

(3)

波浪与透空柱体在相互作用的过程中，将会产生波浪散射和辐射的作用，在流体区域内会相应地出现散射、辐射速度势函数，因此，各流体区域内的势函数可认为是各区域内相关势函数的合成，即：

(4)

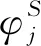
(5)

式中：k0和ω满足色散关系式，当m=0时，βm=1，当m≥1时，βm=2im。

自由表面与等深不透水底面的边界条件为[4]：

(6)

柱体的侧表面由2部分组成，即非透空表面和透空表面，因此柱体表面条件的表达式相应地由2部分组成：

(7)

式中：v=(v1,v2,v3)分别表示透空柱体在纵荡、垂荡以及横摇3个自由度上的运动速度，n为单位法向量，w(θ,z)为流体质点穿越透空圆柱体柱面过程中速度的空间表达式。假设透空柱体的侧面厚度相对较薄，其厚度可忽略不计，流体流经透空表面的过程满足达西定理的条件，根据理想流体的伯努利方程，w(θ,z)正比于透空薄壁前后的压差，即[4]：

w(θ,z)=ik0G0[φ1(a,θ,z)-φ2(a,θ,z)]

(8)

式中：G0=ρωb/(μk0)是表征透空薄壁透水性能的无量纲参数，数值越大，透水能力越强[15]；μ为动力粘度；ρ为流体密度；b为长度量纲的材料特性。

针对波浪与透空柱体相互作用过程中的散射速度势和辐射速度势的求解，流体区域ΩI的远方边界符合Sommerfeld辐射边界条件，即产生的散射波和辐射波会一直向远方传播，不会产生反射现象，其表达式为：

(9)

式中：l=1,2,3分别代表纵荡、垂荡以及横摇3种微幅振荡运动模式。

在流体区域ΩI和ΩII的边界是柱体的透空薄壁部分，根据前述假设，透空薄壁厚度可忽略不计，流体质点在穿越透空圆柱体柱面过程中，流体质点的速度具有连续性，因此，该处的边界条件可表达为：

(10)

流体区域ΩI和ΩIII处于完全贯通的状态，因此流体势函数及流体质点的速度均具有连续性，因此该边界处的边界条件表达式为：

(11)

2 理论模型的解析解

2.1 波浪散射问题

在柱坐标下拉普拉斯方程基本解(的基础上，结合边界条件(6)和(7)，可以对流体区域ΩI内的波浪散射流体速度势函数求解，其表达式为：

(12)

其中：

(13)

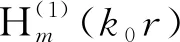
ω2=-gkntan(knh)

(14)

根据式(4)，在不考虑波浪辐射效应的情况下，流体区域ΩI中的速度势函数表达式为：

(15)

(16)

式中：Bmn(m,n=0,1,2,…)是待求解的未知系数，Im(βnr)为m阶经修正的第1类贝塞尔函数，波数βn的计算公式为：

(17)

对于流体区域ΩIII而言，如图1所示，该流域的边界条件与区域ΩII类似，因此求解散射速度势函数的拉普拉斯方程所用的方法相同，经过求解，该流体区域内的势函数表达式为：

(18)

式中Cmn(m,n=0,1,2,…)待求解的未知系数。波数τn的计算公式为：

(19)

综述所述，Amn、Bmn、Cmn为待求解系数，利用r=a处的边界条件(7)、(10)和(11)，结合coskm(z+h0)、cosβm(z+h2)与cosτm(z+h0)分别在积分区间-h0≤z≤0(流体区域ΩI)、-h2≤z≤-h1(流体区域ΩII)和-h0≤z≤-h2内的正交特性，可通过求解线性方程组的途径对上述未知系数进行求解。然后，可以利用伯努利方程计算透空柱体在入射波作用下所受到的波浪力，以流体区域ΩI为例，透空柱体受到的外部波浪力为：

(20)

式中P为由于波浪运动在柱体表面产生的压力，可通过伯努利方程进行求解。根据式(20)，透空柱体在纵荡方向、垂荡方向以及横摇方向上受到的波浪力的求解表达式依次为：

(21)

(22)

(23)

式中：F3为透空浮体的倾覆力矩;(0,0,zc)为倾覆力矩的作用中心。

2.2 波浪辐射问题

(24)

在流体区域ΩI内，根据边界条件(6)和(7)，可分别对透空浮体的纵荡运动、垂荡运动以及横摇运动模式下该流域内的势函数进行求解，势函数的表达式为：

(25)

(26)

(27)

在流体区域ΩII内，根据透空部分上下底面的非透水条件以及柱体表面边界条件(7)，可分别对透空浮体的纵荡运动、垂荡运动以及横摇运动模式下该流域内的势函数进行求解，势函数的表达式为：

(28)

(29)

(30)

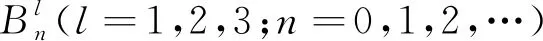
在流体区域ΩIII内，根据底面边界条件(6)和透空柱体下表面的物面条件(7)，可分别对透空浮体的纵荡运动、垂荡运动以及横摇运动模式下该流域内的势函数进行求解，势函数的表达式为：

cos (mθ)

(31)

(32)

(33)

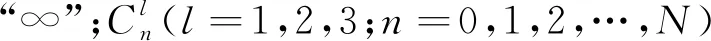
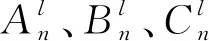
(34)

将透空柱体单位运动速度的势函数(24)代入式(34)，可得透空柱体单位运动速度下所受到的波浪辐射力为：

(35)

根据式(38)可以发现，透空柱体所受到的波浪辐射力的复数表达形式中，附加质量系数与实部有关，阻尼系数与虚部有关，因此水动力系数的表达式为：

(36)

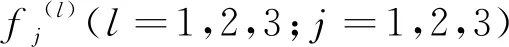
(37)

(38)

(39)

式中(0,0,zc)为透空柱体横摇的运动中心。

3 计算结果与分析

3.1 解析计算方法验证

为验证本论文提出的计算方法的准确性，接下来需要将本论文相关计算结果与已有的研究成果进行对比分析。当G0=0时，透空薄壁变为实心非透水薄壁，Williams等[4]和Bhatta[12]对该极限情况下圆柱体的波浪载荷进行了数值计算。如图2～4所示，分别取h0/a=0.75,h2/a=0.5(图2和图3)和h0/a=5,h2/a=1.2(图4)，其中纵荡、垂荡波浪激振力的无量纲化过程为Λl=Fl/(ρgHπa2)(l=1,2)，横摇激振力的无量纲化过程为Λ3=F3/ρgHπa3。将本文计算结果与文献[4]的结果进行对比，以验证本文解析计算模型的正确性。

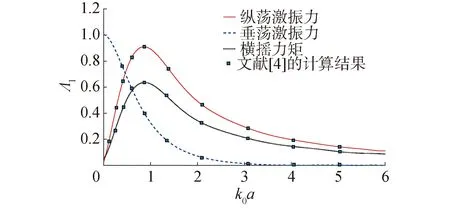
图2 实心圆柱体所受波浪激振力的计算结果

图3 实心圆柱体微幅振荡阻尼系数的计算结果

图4 实心圆柱体微幅振荡附加质量系数的计算结果

3.2 散射激振力分析

在规则入射波的作用下，利用本论文构建的理论计算模型对透空圆柱体受到的散射激振力进行计算，在计算的过程中，设初始输入条件为，h0/a=6,h2/a=2,h1/a=0.5透空系数分别取0.5、5.0和10.0。分析不同透空系数对散射激振力的影响规律，结果如图5所示。透空系数对波浪激振力的影响主要集中在入射波长波较大的情形，尤其是对纵荡和横摇波浪激振力峰值影响较为显著，这对工程应用非常重要。随着透水能力的增强，透空薄壁的有效波浪作用面积将会变小，因此3个自由度方向上的散射激振力均会变小，相比较而言，垂荡激振力的降低幅度最小，横摇力矩的变化最为复杂，需要在工程应用中引起重视。

图5 不同透空系数对散射激振力的影响

3.3 微幅振荡响应特性分析

在规则入射波作用下，利用本论文所构建的理论解析计算模型对透空圆柱体微幅振荡运动过程中的水动力系数(附加质量系数和阻尼系数)进行计算，结果如图6～8所示，在计算的过程中，图(a)所示的无量纲附加质量系数计算结果的初始输入条件为h0/a=5.0,h2/a=1.2,h1/a=0.5；图(b)所示无量纲阻尼系数计算结果的初始输入条件为h0/a=3.0,h2/a=1.0,h1/a=0.5；透空系数分别取0、5.0和10.0。

图6 不同透空系数下纵荡水动力系数的变化趋势

图7 不同透空系数下垂荡水动力系数的变化趋势

在入射波的激励下，随着透空系数的增加，透空薄壁的有效迎浪面积减小，浮体系统受到的波浪激振力也随之减小，导致3个自由度(纵荡、垂荡以及横摇)上的附加质量系数(图6～8中的(a)图)均呈现出减小的趋势，而且在不同的入射波波长范围内，减小的幅度基本一致，即对入射波波长不敏感，这对于维护透空圆柱体的稳定性具有重要意义。阻尼系数的变化则相对复杂，整体来看，增加透空薄壁以后，阻尼系数呈现出增加的趋势；对于纵荡阻尼系数而言，透空系数只有在某一段入射波波长范围内才会对阻尼系数产生较为明显的影响(下降)，且越接近阻尼系数的峰值，这种影响作用就越为明显；在垂荡方向上，透水能力增加以后，在不同的入射波波长范围内阻尼系数的增加率也不相同，当入射波波长较小时，透水能力的增加反而会降低阻尼系数，这一点需要引起注意；在横摇方向上，阻尼系数随入射波波长的变化趋势存在明显不同，甚至是相反的情况，在波长较大或较小时透水能力的增加会导致阻尼系数的上升，但在中间某波长范围内透空圆柱体的透水能力越强，横摇阻尼系数反而会变小。

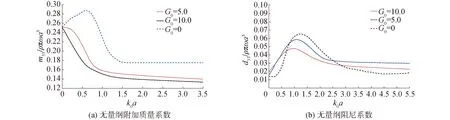
图8 不同透空系数下横摇水动力系数的变化趋势

4 结论

1)透空薄壁只能在入射波低频范围内能够显著降低圆柱体体所受到的纵荡和横摇波浪力(矩)，对垂荡波浪力影响作用较小。

2)从整体上看，透空薄壁能够较好地改善圆柱形结构物的水动力性能，尤其是附加质量系数的改善较为明显，且对入射波波长不敏感，这对于维护透空圆柱体的稳定性具有重要意义。

3)随着透空薄壁透水能力的增大，圆柱形结构物微幅振荡阻尼系数的峰值呈增大趋势，且透空系数越大，阻尼系数峰值的增加也越明显。

本文的研究成果为透空薄壁在浮式圆柱形结构物领域中的工程应用奠定了一定的理论分析基础，可为下一步开展物理模型试验提供一定的理论指导。同时，本文设定的理论计算条件与工程实际存在一定差异，下一步可针对非线性/随机波浪作用下透空圆柱体在六自由度空间内的波浪水动力性能开展数值分析工作。