一维带限分形Weierstrass地面的宽带电磁散射特性研究

陈芬芬，田 炜，葛菁菁

(延安大学物理与电子信息学院，陕西延安716000)

一维带限分形Weierstrass地面的宽带电磁散射特性研究

陈芬芬，田 炜*，葛菁菁

(延安大学物理与电子信息学院，陕西延安716000)

应用微扰法理论并结合一维带限分形Weierstrass功率谱密度推导出了宽带散射系数的计算公式，然后运用微扰法实现了地面宽带电磁散射问题的计算，得到了散射系数随入射波波长的变化曲线。分析了高度起伏均方根、分维数、土壤湿度、温度对散射系数的影响结果。结果表明，高度起伏均方根、分维数、土壤湿度对散射系数的影响明显，而温度对散射系数几乎无影响。

宽带电磁散射；分形粗糙地面；微扰法；散射系数

粗糙面电磁散射特性的研究在海洋工程、雷达探测、环境遥感、辐射定标制导武器的设计、飞行器的隐身以及反隐身等军用、民用领域有着广泛的应用。近年来有关该领域的研究引起了国内外诸多学者们的重视[1-5]，相关的研究方法也在不断的丰富，常用的方法有矩量法[6]、时域有限差分法[7]、基尔霍夫近似法[8]等。目前，有关粗糙面的双站、单站电磁散射特性研究已较成熟，而对于地面宽带电磁散射问题的研究，还属于探索阶段。本文将运用微扰法开展粗糙面的宽带电磁散射特性的研究，粗糙地面选择一维带限分形Weierstrass模型，该模型具有自相似性，又在大、小范围内存在无序的特点，可实现各种复杂的随机粗糙面结构的模拟。通过数值计算得到了散射系数随入射波波长的变化曲线。分析了高度起伏均方根、分维数、土壤湿度、温度对散射系数的影响结果。

1 基本理论

如图1所示，粗糙面将空间分为两部分，上方为自由空间Ω0(ε0，μ0)，下方为各向同性介质空间Ω1(ε1，μ1)，入射波波矢是ki，散射波波矢是ks，θi，θs分别是入射角和散射角。对于一维带限分形Weierstrass地面，其表面高度标准离差比入射波波长小得多(5%或者更小)，而且平均表面斜度可与表面标准离差和波数之积相比拟，或者小于表面标准离差和波数之积，即kδ<0.32(其中k为入射波波数、δ是高度起伏均方根)时，可采用微扰法理论处理粗糙面散射问题。对水平极化平面入射波，散射截面为[9]

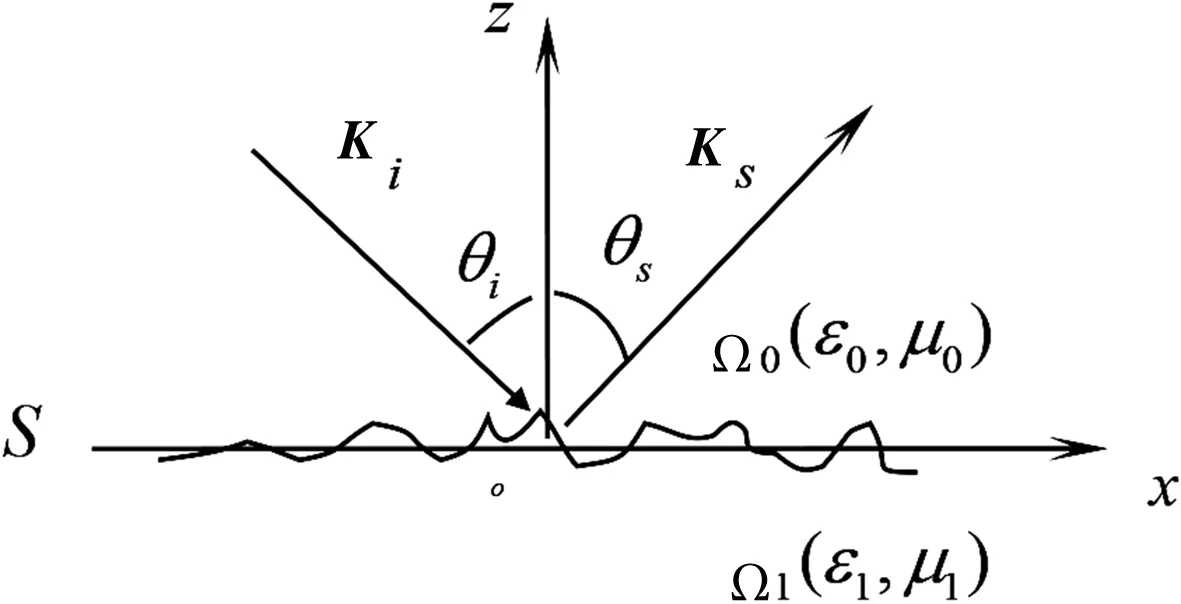
图1 粗糙面电磁散射问题几何示意图

W(kx+ksinθ,ky)η/ηs

(1)

式中，W(kx+ksinθ,ky)为粗糙面功率谱密度，αpq为极化系数，下标p为入射波极化状态，q为散射波极化状态，αpq的数学表达式为

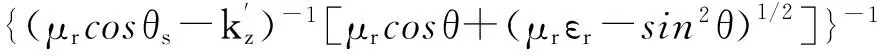
(2)

(3)

一维带限Weierstrass分形函数的自相关函数为[10]

(4)

其中，δ为粗糙面高度起伏均方根，b为空间基频，D为分维数(11，N=N2-N1+1其功率谱密度是自相关函数的傅里叶变换，可表示为

(5)

式中δ(K-sb)n为Dirac函数，如令K=sbn，则功率谱是一个离散谱。当b→1时，采用连续近似方法，该功率谱可写为

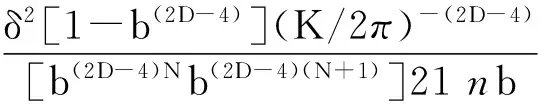
(6)

在自由空间中，入射场与散射场具有相同的本质阻抗，即η=ηs，同时还有k=ks，kx=-ksinθscosφs，ky=-ksinθssinφs。一维介质粗糙面散射截面的表达式为

W(-kxsinθscosφs+ksinθ，ky)

(7)

进一步可得电磁散射系数为

(8)

由(7)式可看出，当入射角、散射角、散射的方位角、粗糙面高度起伏均方根、分维数、介电常数一定时，散射系数受入射波波长的影响。通过数值计算可以得出HH极化状态下，散射系数随入射波波长的变化曲线。

2 数值计算结果与讨论

采用一维带限Weierstrass分形粗糙面来模拟实际地面，如上图1所示。下面取θi=60°，θs=30°，K=2π/20λ，k=2π/λ，b=0.5 e，N=logb(k/K)+1，宽带频率范围为0.1-2GHz，即波长λ范围为0.15-3 m。下面将讨论水平极化状态时，一维带限Weierstrass分形粗糙面的电磁散射问题。

2.1 高度起伏均方根对宽带散射系数的影响

图2给出了高度起伏均方根对散射系数的影响结果，计算中取D=1.1，mv=0.1，T=20 ℃；分别取δ=0.01m，δ=0.02m，δ=0.03m。从图2可以看出，不同起伏均方根对应的曲线区别较为明显，起伏均方根对散射系数的影响较大，在其他条件保持不变的情况下，起伏均方根δ越大，散射系数σ越大。总体来说，散射系数随着入射波波长的增大而减小，也就是说散射系数随着入射波频率的增大而增大。

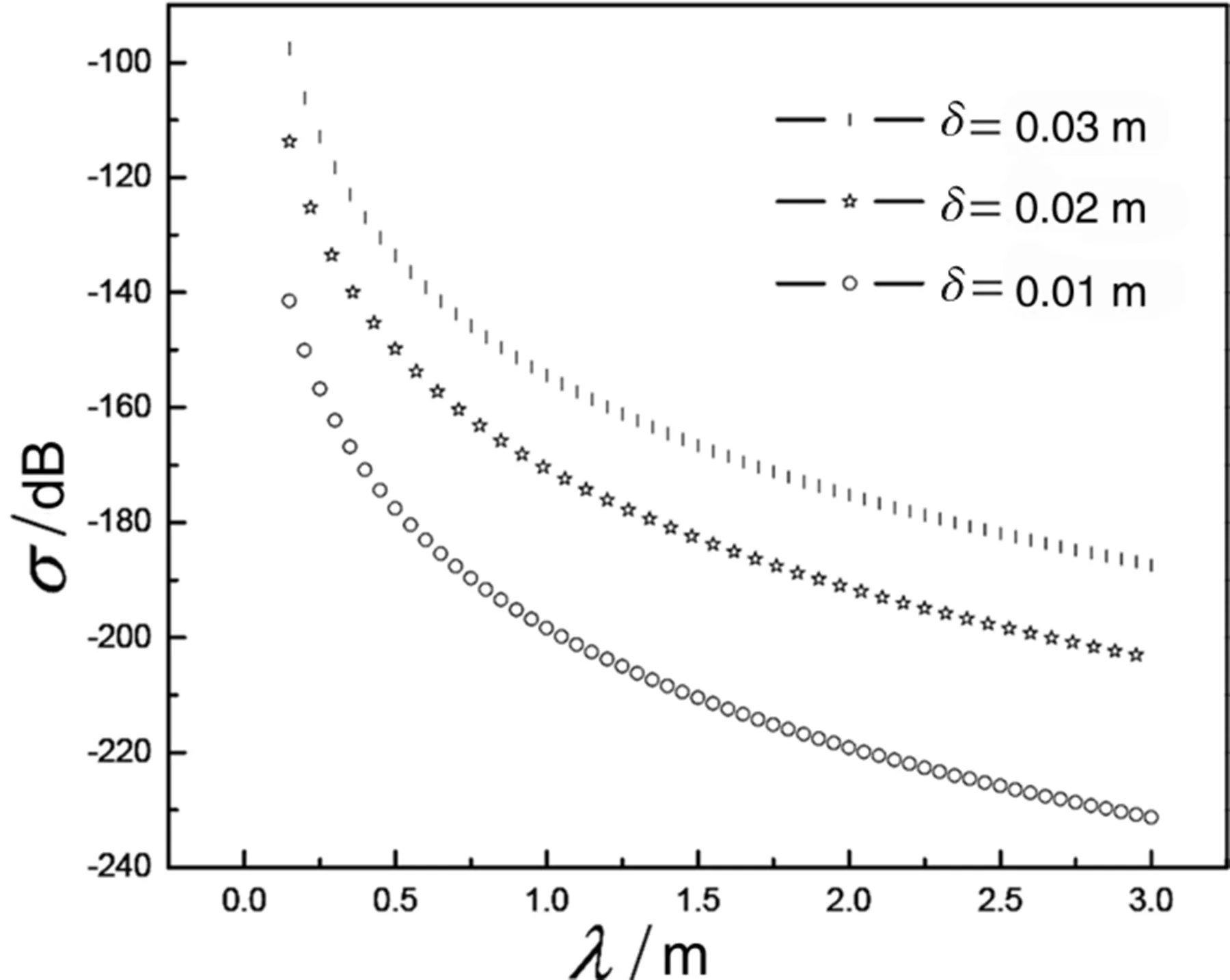
图2 起伏均方根对散射系数影响

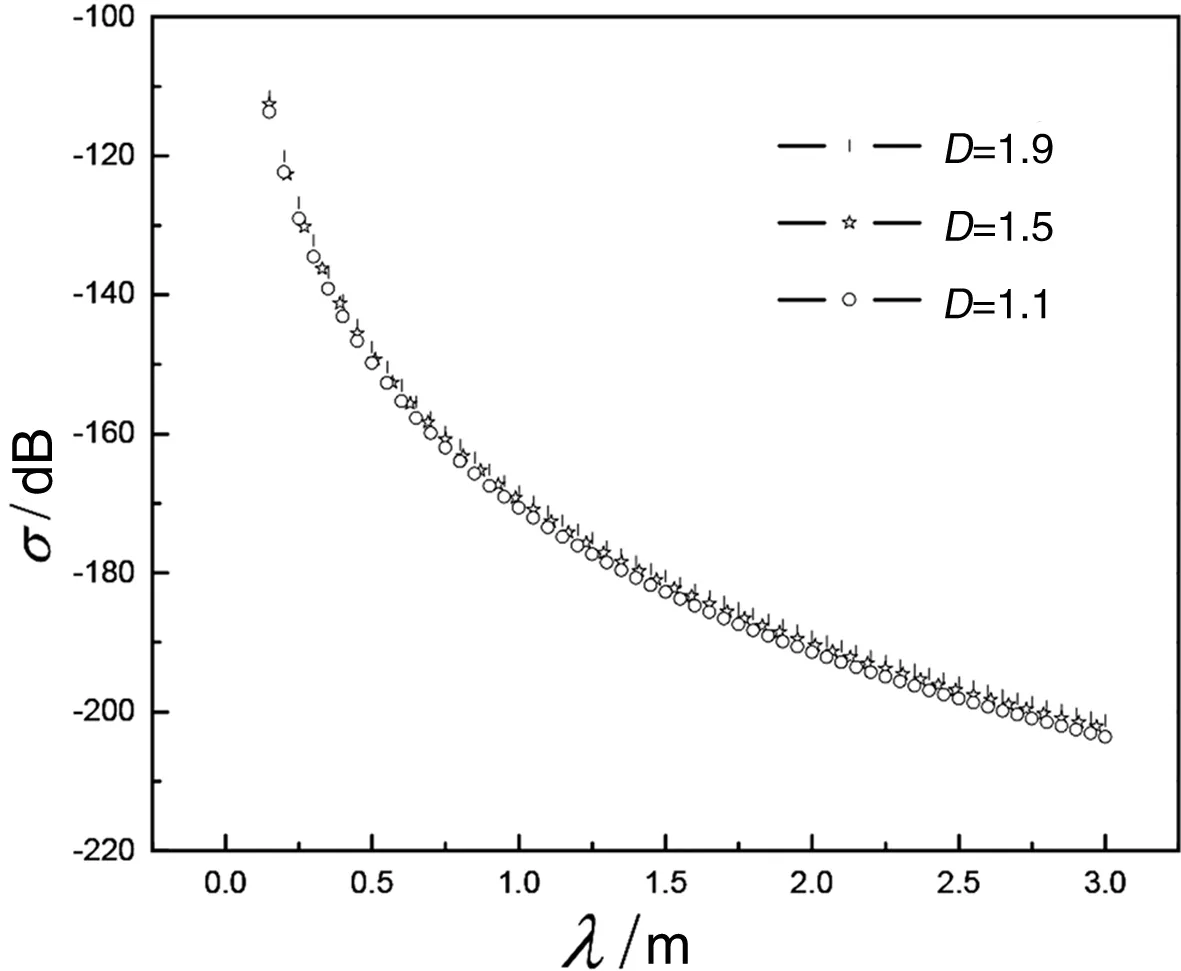
图3 分维数对散射系数的影响

2.2 分维数对宽带散射系数的影响

图3给出了分维数对宽带散射系数的影响结果，计算中取δ=0.02m，mv=0.1，T=20℃；分别取D=1.1，D=1.5，D=1.9。从图3可以看出，不同分维数对应的曲线区别不是很明显，分维数对散射系数的影响较小，在其他条件一定的条件下，分维数越大，散射系数越大，但这种随之增大趋势较为缓慢；总体上，散射系数随着入射波波长的增大而减小，也就是说散射系数随着入射波频率的增大而增大。当λ<0.5m时，散射系数随入射波波长的增大而快速减小；当λ>0.5m时，散射系数随入射波波长的增大而缓慢减小。

2.3 土壤湿度对宽带散射系数的影响

图4给出了土壤湿度对宽带散射系数的影响结果，计算中取δ=0.02m，D=1.1，T=20℃；分别取mv=0.1，mv=0.2，mv=0.3。由参考文献[10]可知mv=0.1时ε=4.9238-0.1547i；mv=0.2时ε=10.2394-0.4484i；mv=0.3时ε=18.1228-0.8852i。由图4可以看出，不同土壤湿度对应的曲线区别不是很明显。当其他条件一定的情况下，散射系数随着湿度的增大而增大但增大趋势缓慢；而同一湿度条件下，散射系数随着入射波波长的增大而减小，即散射系数随着入射波频率的增大而增大，当λ<0.5m时，散射系数随入射波波长的增大而快速减小；当θ<0.5m时，散射系数随入射波波长的增大而缓慢减小。

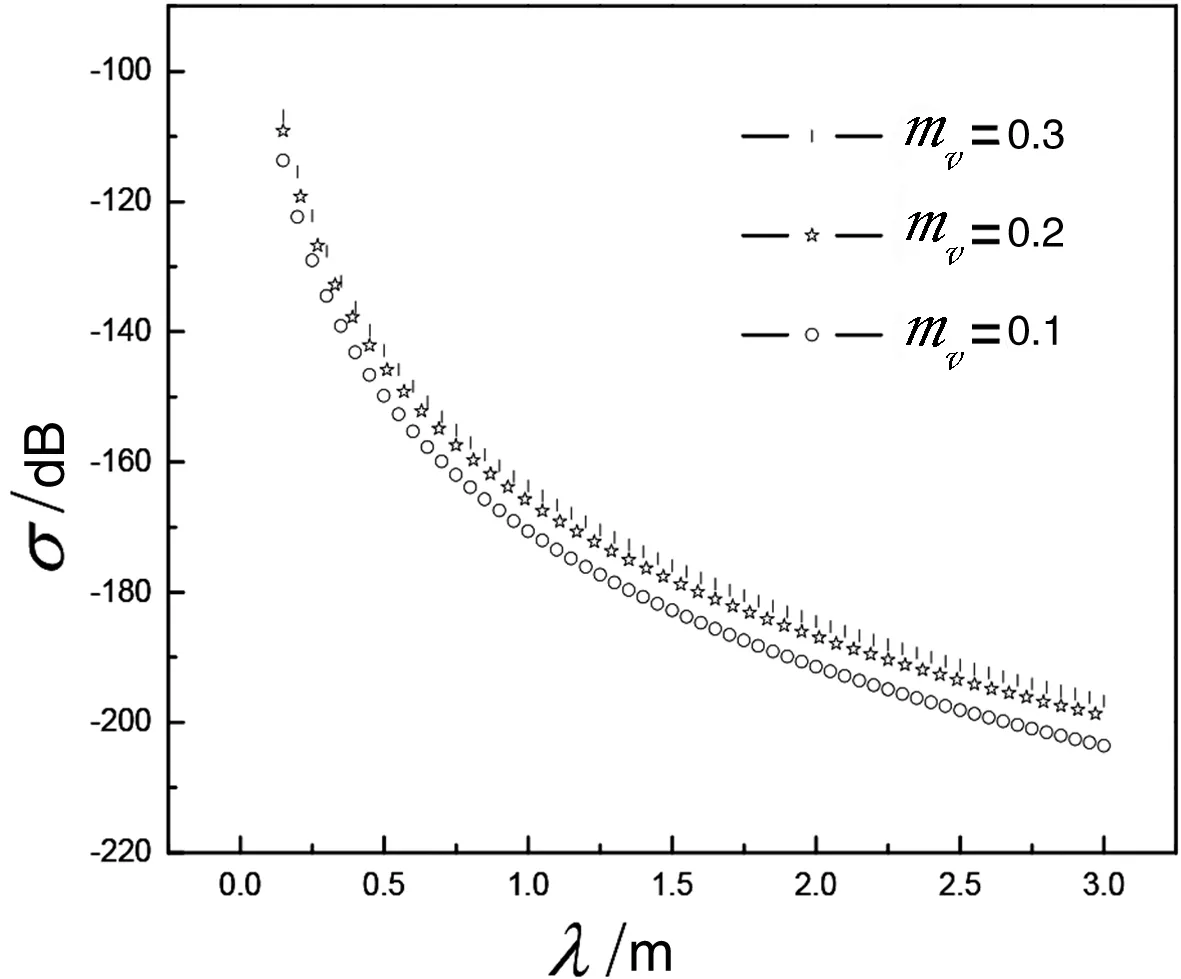
图4 湿度对散射系数的影响

2.4 土壤温度对宽带散射系数的影响

图5给出了土壤温度对宽带散射系数的影响结果，计算中取δ=0.02m，D=1.1，mv=0.1；分别取T=0℃，T=10℃，T=20℃。由参考文献[10]可知T=0℃时ε=5.083-0.26i；T=10℃时ε=5.00-0.20i；T=20℃时ε=4.92-0.15i。由图5可知，温度对散射系数几乎没有影响，即在研究散射系数时可以不考虑温度这个因素，为散射系数的研究提供了方便。总体来说，散射系数均随着入射波波长的增大而减小，即散射系数随着入射波频率的增大而增大，当时，散射系数随入射波波长的增大而快速减小；当λ<0.5m时，散射系数随入射波波长的增大而缓慢减小。

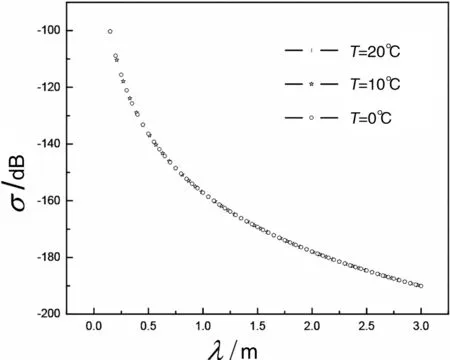
图5 温度对散射系数的影响

3 结束语

当平面电磁波入射到一分形粗糙面上时，发生在介质表面的电磁散射在诸多实际问题中有着广泛的应用。本文运用微扰法理论并结合一维带限分形Weierstrass功率谱密度推导出了宽带散射系数的计算公式。然后运用微扰法实现了地面宽带电磁散射问题的计算，得到了散射系数随入射波波长的变化曲线。分析了高度起伏均方根、分维数、土壤湿度、温度对散射系数的影响结果。这些结果在海洋工程、雷达探测、环境遥感、辐射定标制导武器的设计、飞行器的隐身以及反隐身等军用、民用领域有着广泛的应用。当然，这里只是研究了粗糙面高度起伏均方根、分维数、土壤湿度、温度及入射波波长对一种比较简单的一维带限Weierstrass分形粗糙面HH极化散射系数的影响，对于其他谱分布以及更加复杂的粗糙面散射问题还需要做更深层次的研究。

[1]Yaёl D,Laetitia T Le,Vincent G. Modelling of the electromagnetic scattering by sea surfaces at grazing incidence application to HF surface wave radars[J]. Comptes Rendus Physique,2010,11(1): 87-95.

[2]Menedez J,Pinczuk A.Light scattering determinations of band offsets in semiconductor heterostructures[J]. IEEE Journal of Quantum Electronics,1988,24(8):1698-1710.

[3]Tsang L,Kong J A,Ding K H.Scattering of electromagnetic waves[M].New York: John Wiley&Sons Inc，2001.

[4]Eric I T.The validity of the perturbation approximation for rough surface scattering using a gaussian roughness spectrum[J].Acoust Soc Am,1989，86(1)：261-277.

[5]Elfouhaily T M,Johnson J T.A new model for rough surface scattering[J].IEEE Trans.on GRS,2007,45(7):2300-2308.

[6]田炜，郝伟杰.一维带限Weierstrass分形海面电磁散射的矩量法研究[J].科学技术与工程，2011，(26)：6319-6322.

[7]朱小敏，任新成.分形地面与埋藏目标宽带电磁散射FDTD研究[J].河南科学，2014，32(9)：1713-1718.

[8]田炜.粗糙面后向散射的基尔霍夫标量近似法研究[J].河南科学，2013，31(1)：62-65.

[9]任新成，郭立新.一维带限Weierstrass分层介质粗糙面电磁散射研究[J].西安电子科技大学学报，2009，36(2)：322-330.

[10]Wang J R,Schmugge T J.An empirical model for the complex dielectric permittivity of soils as a function of water content[J].IEEE Transactions on Geoscience and Remote Sensing,1980, 18: 288-295.

[责任编辑 贺小林]

Investigation on Broadband Electromagnetic Scattering from One-dimensional Band-limited Fractal Weierstrass Ground

CHEN Fen-fen,TIAN WEI*,GE Jing-jing

(College of Physics and Electronic Information,Yan′an University,Yan′an 716000,China)

Firstly small perturbation method is applicated.The broadband scattering coefficient calculation formula is derived combined with 1D band-limited Weierstrass fractal power spectral density.Then the calculation of wide-band electromagnetic scattering problem of the ground is studied using small perturbation method. The curves of the scattering coefficient with varying of wavelength of the incident wave is derived.The influence of the root-mean-square of height fluctuation,fractal dimension,the moisture capacity of soil,temperature of soil on the scattering coefficient is discussed. The results show that the scattering coefficient is influenced by the root-mean-square of height fluctuation,fractal dimension and the moisture capacity of soil,while temperature of soil has little effect on the scattering coefficient.

broadband electromagnetic wave scattering; small perturbation method; fractal rough ground; the scattering coefficient

2015-09-12

2013年国家级大学生创新创业训练计划项目(201310719020)

陈芬芬(1992—)，女，湖北咸宁人，延安大学物理与电子信息学院学生。 *为通信作者

TN011

A

1004-602X(2015)04-0044-04