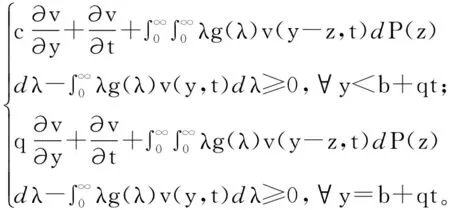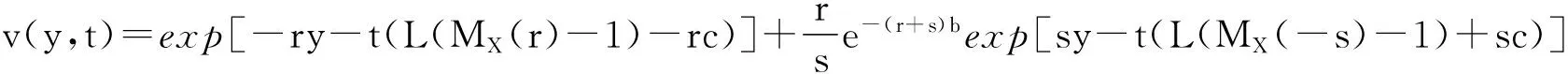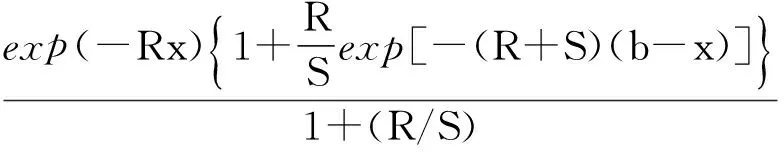条件Poisson风险模型破产概率与破产时间期望的界限

张莉莉，李志民

(安徽工程大学数理学院，安徽芜湖241000)

条件Poisson风险模型破产概率与破产时间期望的界限

张莉莉，李志民

(安徽工程大学数理学院，安徽芜湖241000)

推广了经典的风险模型。对于索赔次数，我们用一个条件泊松过程刻画，通过构造一个下鞅，在破产时盈余为零的假设基础上给出了索赔到达为条件Poisson过程的风险模型破产概率的下界和破产时刻期望的上界；对于带红利情形，我们在红利线为线性情况下，给出了破产概率的下界。

风险模型；条件泊松；破产概率

经典风险模型中，t时间内索赔平均次数是λt，而在实际生活中，强度(或速率)λ不一定满足常数的条件。意外事故发生的频率往往受某种因素的影响，当这种因素是主导因素时，事故发生的强度可看作一个常数(即经典模型中的λ)，而当这种影响因素变动于主导因素与次要因素之间，事故发生的强度即是变化的，可见，将强度λ作为随机变量来研究是合理的。在实际的保险业务中，为了鼓励投保人自我防范风险，减少可避免的公司与投保人的双重损失，常会设置对投保人的红利政策——设定一个红利界限，盈余在红利界限下，便不发放红利，若盈余在红利界限上，每单位时间发放固定的红利，直至下一次索赔发生。

为了获得更加贴近实际情况的分析，众多学者对经典模型的推广做了大量研究。Li和Garrido[1]把经典风险模型中对罚函数折现的研究推广到了Sparre Andersen模型，其中时间间隔分布满足Erlang(n)分布。文献[2]中将经典风险模型推广到了索赔到达为普通更新过程的风险模型，并研究了常数红利界限下的破产的相关问题。Albrecher等[3]在Erlang(n)风险模型的基础上加上了常数红利因素，研究了红利支付的折现分布与其相应的矩。Grandel[4]对于非齐次Poisson风险模型、Cox风险模型、更新风险模型与平稳风险模型中破产概率等问题进行了研究。文献[5]利用鞅技巧获得了索赔计数过程为任意计数过程情形且保费收取为随机情形时的破产概率的上界。在红利问题中，一个重要的因素是红利的折现分布。Dickson和Waters[6]研究了常数红利界限下，红利支付折现分布的n阶矩，而Albrecher等[7]将红利折现分布的n阶矩推广到了线性红利中。对于非线性红利模型的研究，见Albrecher等[8]。Lourdes B.Afonso[9]用新的方法——对偶的方法，证明了有关多值红利的折现期望等量。条件泊松过程的一些基本性质见文献[10]。

在已有的文献中，索赔速率的描述用一个线性函数或者是一个非线性函数，而在实践中，由于受到各种因素的影响，速率是变化和不可知的，为此，本文中我们将速率视为一个随机变量，研究相应的问题。在第一节中，我们介绍基本的模型和一些概念、记法和主要结论；在第二节中，我们给出主要结论的证明；最后一节中，我们讨论带有红利情形的破产概率的下界。

1 条件泊松风险模型

为了更好地描述我们的模型，首先介绍条件泊松过程。令N(t)是一个计数过程，存在一个正随机变量Λ，其期望记为L，在Λ=λ条件下，这个计数过程是速率为λ的泊松过程，这样的计数过程称为条件泊松过程。

我们设Λ是一个连续随机变量，其密度函数记为g，从而从时刻s到时刻t+s时保险公司的索赔次数的分布为

P[N(t+s)-N(s)=n]=

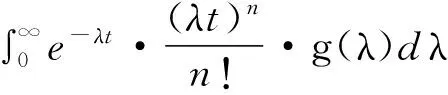
假设保险公司的保费的收取是按照速率c，在一定时间的索赔次数是一个条件泊松过程，保险公司在时刻t的盈余Rt就可以用下面过程来描述

Rt=x+ct-St，

其中，St=x1+x2+…+xN，St为t时刻为止的总索赔额，其中N为条件泊松过程，xi之间独立同分布且xi与N之间相互独立。

设MX(-r)为索赔额xi的矩母函数，类似于文献[11]，我们可以算出St的矩母函数为

MSt(-r)=E[e-rSt]=E[E(e-rSt|N)]=

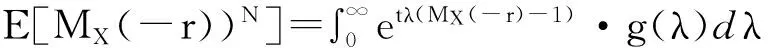
记保险公司初始资产为x时的破产概率为

Ψ(x)，T为保险公司破产的时刻，P(z)为个体索赔额的分布函数，我们有

Ψ(x)=P(T<∞|X0=x)。

在上面基本假设下，我们有下面两个主要结果：

定理1 对于条件泊松风险模型，初始资产为x的破产概率Ψ(x)具有下界，即Ψ(x)≥exp(-Rx)，其中R是L(MX(-r)-1)+rc=0的解。

定理2 若条件泊松风险模型中计数过程具有独立增量，破产时刻T的期望有

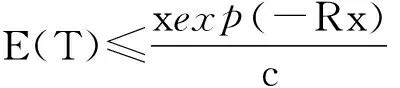
其中R是L(MX(-r)-1)+rc=0的解。

2 定理的证明

定理1 证明：考虑负索赔额模型，Rt=x+St-ct，易证若存在一个随机变量V(x)，当V(x)为下鞅时，有

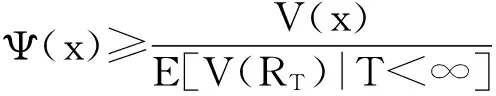
(2.1)

设Yt+s=exp[-r(Rt+s+c(t+s))]，

Yt=exp[-r(Rt+ct)]，则有

设Ht是t时刻以前的信息，L是λ的期望，则由条件泊松过程的平稳增量性，我们有

E[Yt+s|Ht]=E[exp(-r(St+s-St))]·Yt

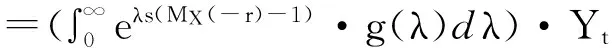
从而我们有

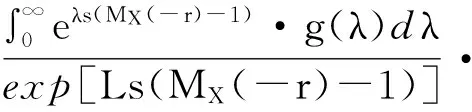
记f(λ)=exp[λs(MX(-r)-1)]，我们易知

f(λ)是一个凸函数，从而有E[f(λ)]≥f[E(λ)]，即我们有

exp[Ls(MX(-r)-1)]。

从而我们有

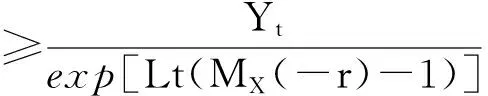
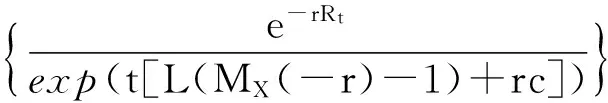
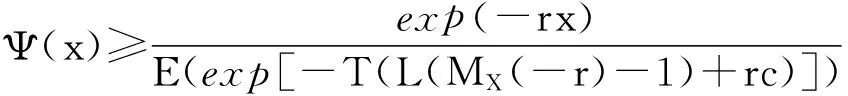
令R是L(MX(-r)-1)+rc=0的解，我们有

Ψ(x)≥exp(-Rx)。

定理2 证明：考虑负索赔额模型，Rt=x+St-ct，当条件泊松过程有独立增量时，设St矩母函数为Mt(-r)，易证有Mt+s(-r)=Mt(-r)·Ms(-r)。同定理1讨论知

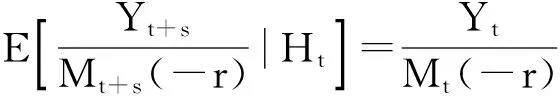
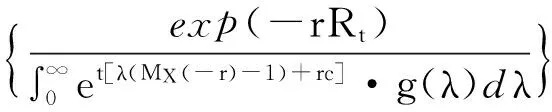
令RT=0，有

=exp(-rx)，

等式两边关于r求导，

=-xexp(-rx)。

注意到

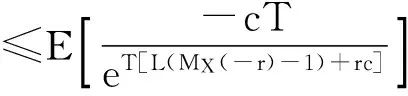
也就是

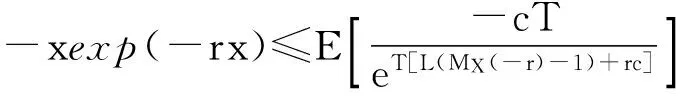
令R是L(MX(-r)-1)+rc=0的解，对于上式做个简单的变形，我们有

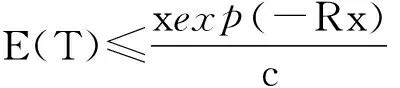
3 正索赔模型带红利的破产概率的下界

下面我们讨论正索赔模型，即Rt=x+ct-St，考虑了红利的发放，设红利界限为y=b+qt，其中b为初值(x≤b)，q为递增速率(0

当v(y,t)为下鞅时，满足

等价于：

考虑下述函数：

v(y,t)是一个下鞅，参见文献[11]。

-qr-L·Mx(r)+cr=qs-LMX(-s)-cs，排除s=-r的解。

令R是L(MX(r)-1)-rc=0的正解，S为R=r时的s之正值。

因为v(x,0)≤E[v(RT,T)|T<∞]·Ψ(x,b)，我们有

Ψ(x,b)≥

[1]LiS,GarridoJ.OnruinfortheErlang(n)riskprocess[J].Insur.Math.Econ.,2004,34:391-408.

[2]LiS,GarridoJ.Onaclassofrenewalriskmodelswithaconstantdividendbarrier[J].Insur.Math.Econ.,2004.35:691-701.

[3]AlbrecherH,HartingerJ,TichyRF.Onthedistributionofdividendpaymentsandthediscountedpenaltyfunctioninariskmodelwithlineardividendbarrier[J].Scand.ActuarialJ.,2005,2:103-126.

[4]GrandellJ.Aspectsofrisktheory[M].NewYork:Spring,1991.

[5]DeVylderF.Martingalesandruininadynamicalriskprocess[J].ScandinavianActuarialJournal,1977,2:217-225.

[6]DicksonDCM,WatersHR.Someoptimaldividendproblems[J].ASTINBull,2004,34 (1),49-74.

[7]AlbrecherH,HartingerJ,TichyRF.Onthedistributionofdividendpaymentsandthediscountedpenaltyfunctioninariskmodelwithlineardividendbarrier[J].Scand.ActuarialJ,2005,2:103-126.

[8]AlbrecherH,KainhoferR.Risktheorywithanon-lineardividendbarrier[J].Computing,2005,68 (4):289-311.

[9]Lourdes B Afonso,Rui M R Cardoso,Alfredo D.Egídio dos Reis.Dividend problems in the dual risk model [J].Insurance:Mathematics and Economics,2013,53: 906-918.

[10]Ross S M.Stochastic Processes,2nd edition[M].New York: John Wiley & Sons,1996.

[11]Gerber H U.数学风险论导引[M].成世学,严颖,译.北京：世界图书出版公司，1997.

[责任编辑 毕 伟]

Boundary of Ruin Probability and Expectation of the Ruin Time in Conditional Poisson Risk Model

ZHANG Li-li,LI Zhi-min

(School of Mathematics and Physics,Anhui Polytechnic University,Wuhu 241000,China)

We generalized the classical risk model and used a conditional poisson process to describe the claim arrival,by constructing a submartingale,based on the assumption that the surplus is zero when ruin,we gave a lower bound of ruin probability and the upper bound of the expectation of ruin time on the conditional poisson risk model,in the case of the dividend,we gave the lower bound of the ruin probability when the dividend line was a linear case.

risk model; conditional poisson; ruin probability

2015-07-10

安徽省自然科学基金(1508085MA02，1408085QA09)；安徽省高校自然科学基金重点项目(KJ2013A044)

张莉莉(1988—)，女，山西晋城人，安徽工程大学硕士研究生。

O211.9

A

1004-602X(2015)04-0018-03