围护结构对单层轻钢厂房动力特性影响分析

曾滨， 许庆,2， 王浩， 许涛， 李雨航， 邓扬

(1.中冶建筑研究总院有限公司， 北京 100088； 2.清华大学 土木工程系，北京100084； 3.东南大学 土木工程学院， 江苏 南京 210096； 4.北京建筑大学 土木与交通工程学院， 北京 100044)

钢结构厂房因施工速度快、抗震性能好、造价低等特点得到了广泛关注与应用。然而在设计中，工程师仅考虑了主体结构与支撑刚度，常常会忽略围护结构的平面内刚度贡献[1]，使得钢结构厂房的地震作用难以精确计算分析，因此，有必要针对围护结构对钢结构工业厂房动力特性的影响开展深入的分析研究[2-4]。

结构动力特性是分析结构抗震性能的重要指标，其准确计算是工业厂房抗震设计与性能评估的重要基础[5-10]。近年来，学者们开始关注围护结构对工业厂房动力特性及地震响应的影响，Korkmaz等[5]研究了砌体围护墙对钢筋混凝土(RC)预制工业厂房的影响，发现砌体围护墙可显著增强结构的刚度，但其自重会导致地震作用显著增大。Ercolino等[6]研究了预制RC板对单层RC工业厂房抗震性能的影响，发现考虑围护结构后，厂房会在较小的地震烈度下发生破坏失效。Magliulo等[8]分析了围护结构对RC预制工业厂房自振周期的影响，发现相较于简单排架结构模型，考虑围护结构的厂房结构横向一阶基本周期最大可减小80%。综上所述，围护结构对工业厂房的动力特性与抗震性能的影响不可忽略，而基于简化模型的厂房基本周期预测是较为常用的方法。

在钢结构工业厂房的设计中，主要有横向平面模型和三维空间模型2种建模方法[6,11]，但结构计算模型中均未考虑围护结构，计算得到的动力特性与实际情况可能存在较大偏差。同时，以往研究大都针对围护结构本身与连接件进行分析计算，对于围护结构设计参数在整体厂房中的影响研究较少。

本文以大型单层钢结构工业厂房为研究对象，首先开展了厂房动力特性的实测试验，在此基础上，提出了厂房有限元建模策略与围护结构模拟方法，并与实测结果进行了对比，验证了模型的可靠性。针对此种体量的钢结构厂房，提出了影响厂房动力特性的围护结构控制设计参数，并对其影响规律进行了分析。提出刚度与质量修正系数，建立了其与围护结构设计参数的相关性模型。最后提出了基于简化模型的基本周期实用预测公式，并对其进行了验证，同时给出了公式的适用范围。

1 钢结构厂房动力特性现场实测

1.1 结构概况

某单层钢结构厂房位于北京市大兴区，如图1所示，主要用于钢结构构件的加工与拼装。基本设计信息为：1)结构为单层门式刚架结构，钢柱采用等截面实腹柱，截面为H600 mm×320 mm×10 mm×14 mm，屋架采用变截面H型钢梁，截面为H(800～500) mm×220 mm×6 mm×10 mm，门式刚架钢梁之间采用系杆与水平支撑连接，钢柱之间采用柱间支撑与吊车梁进行连接，门式刚架横向共3跨，每跨间距24 m；纵向共有33榀，榀距9 m。采用双层吊车梁，标高分别为5.176 m和7.920 m，屋面檐口标高为11.65 m，室内地坪标高为±0.00，室外地坪标高为-0.35 m；2)屋面与墙面板均采用YX-76-344-688型镀铝锌压型钢板，即波高为76 mm，波距为344 mm，板的有效覆盖宽度为688 mm，板厚为0.8 mm[12]。17与18号轴线处设有抗震伸缩缝，将厂房分割为2个部分。本次测试主要对东侧厂区开展了现场实测，该部分共包括16榀刚架，长度为135 m，如图2所示。

图1 实测单层工业厂房

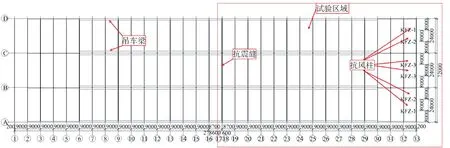
图2 钢结构厂房平面图

1.2 动力特性实测方案

因厂房体量较大，采用环境激励法进行模态分析(operational modal analysis，OMA)[13]。实测采用东华DH5907 N无线结构模态采集仪和DHDAS动态信号采集分析系统。结合现场与设备情况设置了3个工况，分别为长轴平动工况、短轴平动工况与扭转工况，其测点布置如图3所示。平动工况为考虑吊车梁刚度突变，沿高度方向布置3个测点，分别在地面、下层吊车梁与上层吊车梁。经过多次调试分析对比，现场采样频率为20 Hz。

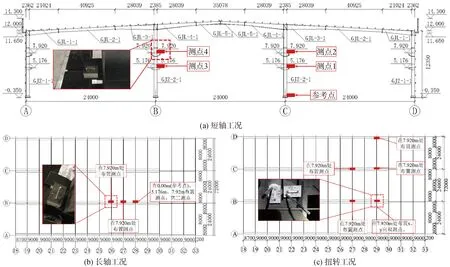
图3 测点布置图

1.3 测试结果与模态参数识别

分别采集各工况下测点振动速度时程信号，对该信号加汉宁窗并进行快速傅里叶变换，采用自互功率谱法分别得到3个工况每个测点的自功率谱密度函数如图4所示。

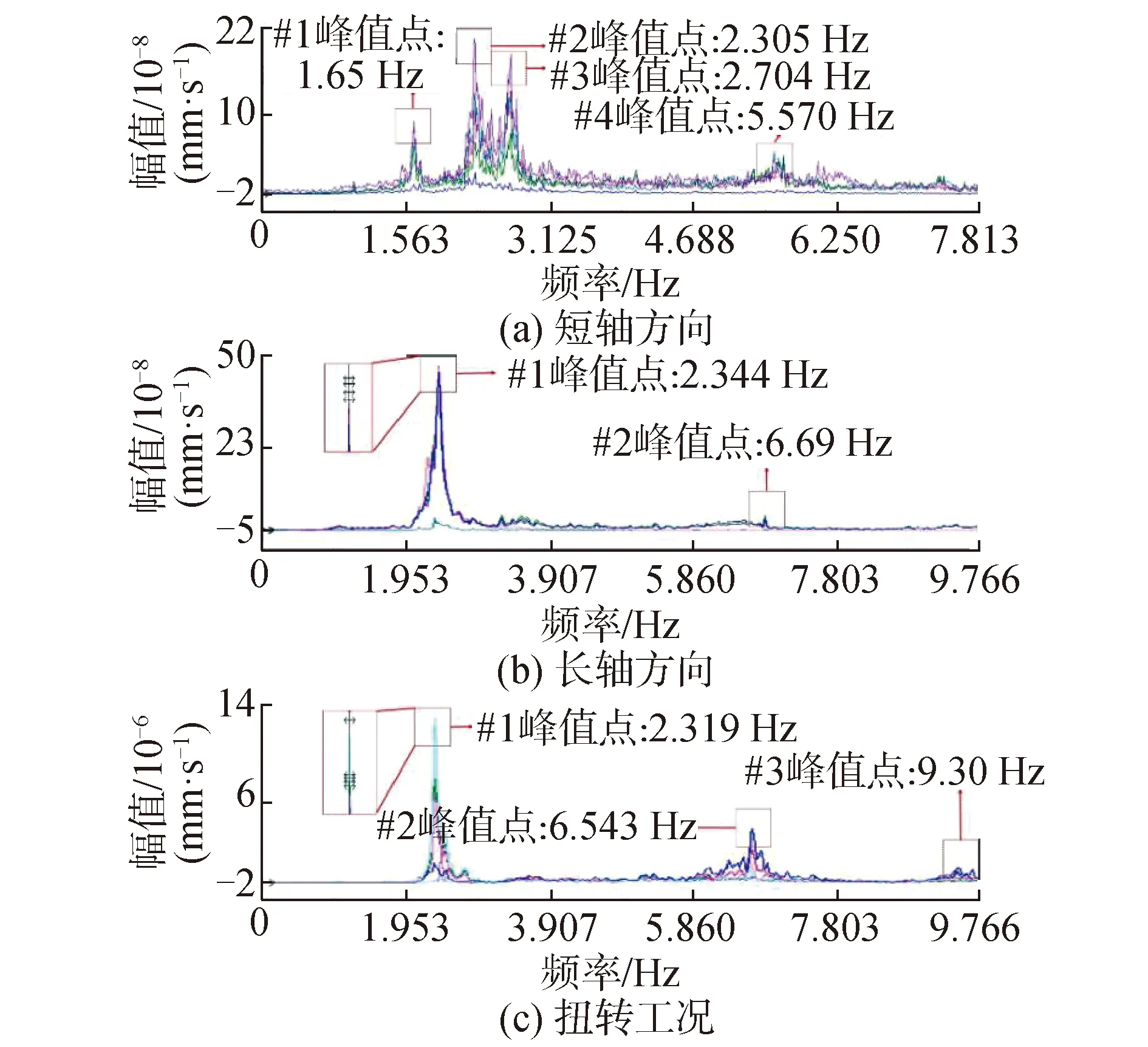
图4 实测响应的功率谱密度函数

从图4中可清晰地辨识出各个工况的峰值点，其中短轴工况有4个峰值点，长轴工况有2个峰值点，扭转工况有3个峰值点。通过对模型振型及MAC模态验证进行分析可知，短轴工况与扭转工况均激励起2阶模态，而长轴工况激励起1阶模态，且模态识别效果较好。通过时域多参考点模态分析法进行模态参数识别[14-15]，钢结构厂房的自振周期如表1所示。

表1 实测动力特性

表1中第1阶振型为UX短轴方向，而第2阶振型为扭转方向，其主要原因在于厂房的纵向布置了柱间支撑、屋面支撑、水平系杆，使得厂房UY刚度变强，RZ刚度相对较弱[16-18]，同时，厂房仅在长轴的一侧布置了山墙(33号轴线)，另一侧未布置山墙(18号轴线)。

2 单层钢结构厂房有限元模拟

2.1 有限元建模策略

为模拟典型单层工业厂房的动力特性，根据上述设计资料，建立2种不同精细程度的有限元模型，分别为简化模型M1和精细模型M2。首先，采用SAP2000建立仅含主体结构的单厂模型M1，如图5(a)所示。采用梁单元模拟纵向柱列、抗风柱与支撑等主体结构构件。为有效传递荷载，根据几何尺寸建立了次梁。柱脚、门式刚架各梁柱及屋脊连接处视为刚接，支撑体系与主体为刚接，抗风柱两端铰接，吊车梁与牛腿为铰接。同时将非结构构件的荷载以面荷载形式转换至结构构件上[19-20]。

在M1模型的基础上，建立考虑围护结构的精细模型M2，如图5(b)所示。M2模型增加了檩条、隅撑、压型钢板等围护结构。墙、屋面压型钢板简化为正交异性壳单元，简化方法在2.2节详细介绍。值得注意的是，为准确模拟檩条与主体结构的搭接关系，在檩条与主体连接处增设短柱，短柱长度由檩条及钢架梁的截面高度确定，短柱和隅撑下端与刚架视为刚接，上端与檩条翼缘为铰接[21-22]。模型中，假定各铰接和刚接节点均视为理想连接，材料为线弹性，模型中不考虑板与板之间的接缝连接影响且不考虑连接件的破坏对结构的影响。

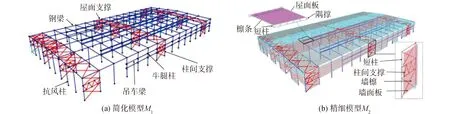
图5 单层钢结构工业厂房有限元模型

2.2 围护结构有限元模拟方法

围护结构有限元建模的重点在于屋面、墙面构件的合理模拟，随着建筑材料的不断发展，单层钢结构厂房的围护结构趋于轻型化，屋面、墙面围护结构大多采用轻型压型钢板与夹层保温材料组成，如图7所示。压型钢板材料本身是各向同性的，但由于特殊的几何构造特征，其整体力学性能表现为正交各向异性。在建模时，可采用壳单元完全精细模拟压型钢板的每个波形，但此方法工作量大，且模型单元数量多，导致计算耗时长，因此，本文采用等效各向异性板方法对压型钢板进行建模[23-24]。

根据压型钢板的研究成果[21-24]，令其材料弹性模量为E0，如图7(a)所示，假设在压型钢板y向施加集中力P，则压型钢板在y向产生的位移为：

(1)

式中：l为压型钢板展开长度；L为压型钢板在y轴方向上的长度；t为不包括镀层或覆层的板厚。相应地，如图7(b)所示，在等效正交各项异性板y方向上施加相同集中力P，则y向产生的位移：

(2)

式中：a为等效正交各向异性板长；Eyy为等效正交各向异性平板在y向的弹性模量。根据等效原则可得Eyy=E0l/a，则μyx=μ0，其中μ0为压型钢板钢材的泊松比，可得Exx为：

(3)

式中：I0为图7(b)等效正交各向异性板的惯性矩；Ix为图6(a)中压型钢板关于X轴的惯性矩；ξ为修正系数，一般可取2～2.5。考虑到Exxμyx=Eyyμxy，可得：

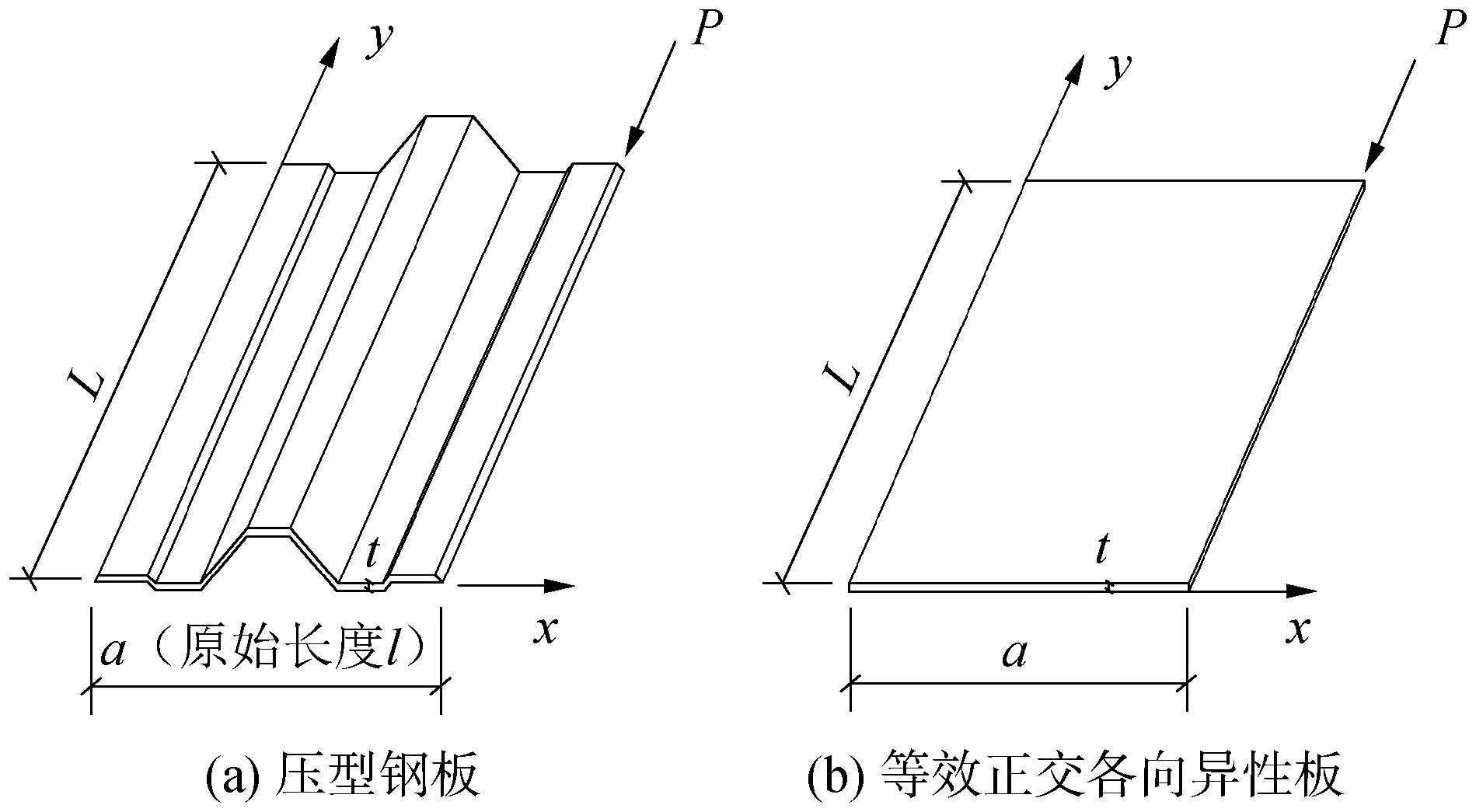
图6 等效正交各向异性板示意

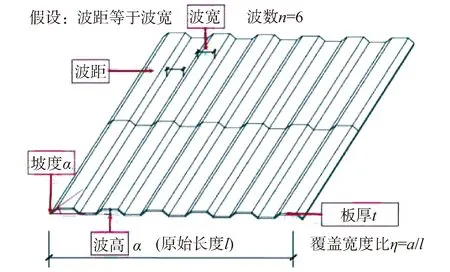
图7 压型钢板简化图

(4)

正交各向异性板的等效剪切模量Geff为：

(5)

式中G0为钢材的剪切模量。

根据上述等效方法与1.1节所述压型钢板类型，得到屋面和墙面压型钢板等效正交各向异性板的材料属性，如表2所示。同时，根据设计图纸可知，屋面压型钢板波纹垂直于檩条(图6(a)的y轴与檩条垂直)，而墙面压型钢板波纹与墙梁垂直(图6(b)的y轴与墙梁垂直)，因此，根据上述位置关系赋予等效正交各向异性壳单元相对应的材料属性。

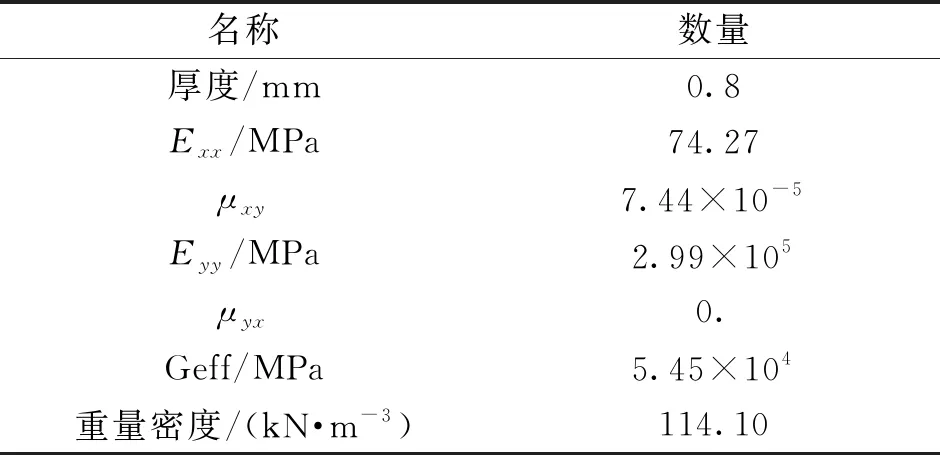
表2 压型钢板等效各向异性板材料属性

2.3 动力特性对比分析

表3给出了有限元计算与实测的结构基本周期对比，可以看出M1模型的三向基本周期均大于实测结果，说明建模时不考虑围护结构会低估结构地震响应，偏于不安全。若利用简化模型计算厂房的动力特性，则需要首先通过精细模型建立预测经验公式。相反地，M2模型计算得到的结构基本周期与实测结果吻合良好。上述结果表明，在进行钢结构工业厂房抗震设计分析中，应该考虑围护结构对结构整体刚度的贡献，仅考虑主体结构构件的计算模型难以准确模拟钢结构厂房的动力特性及结构地震响应。本文提出的M2模型建模策略及围护结构有限元模拟方法，动力特性计算精度较高。

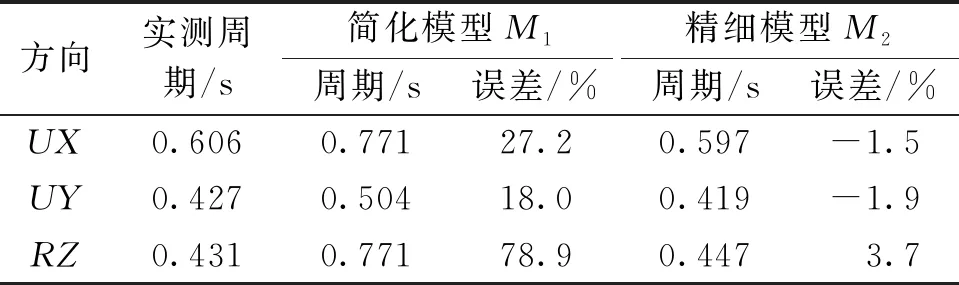
表3 实测与计算基本周期对比

3 围护结构设计参数对结构动力特性的影响规律

以M2模型为基础，分析围护结构设计参数对结构动力特性的影响规律。围护结构主要为压型钢板，具有重量轻、施工快速方便、可选型号类型较多的优势，在单层钢结构工业厂房的围护结构中得到了广泛的应用，压型钢板主要的设计参数有波高、板厚与波宽等。因压型钢板种类较多，为方便计算，可合理假定压型钢板的波距与波宽相等。屋面与墙面围护板采用相同压型钢板类型，屋面围护板强轴沿横向布置，墙面围护板强轴沿高度方向布置。

2.2节分析表明，围护结构的刚度主要由等效正交异性板的材料属性决定，但Exx等参数与多个设计参数耦合相关。因此，本文根据图7假定以下4个主要控制设计参数，分别是：板厚(t)、压型钢板覆盖宽度比(η)、每米波数(n)与钢板坡度(α)。其中，覆盖宽度比应按照η=a/l(等效正交各向异性板长/原始长度)计算，每米波数为成型钢板的波数。经过对常用的成品压型钢板进行调研统计[25]，4个主要控制参数的取值范围如表4所示。

表4 压型钢板参数的取值范围

3.1 板厚的影响分析

开展围护结构压型钢板板厚对结构基本周期的影响分析，以图6(b)中的精细模型M2为基础，建立2组有限元模型S1与S2。

S1模型中覆盖宽度比为51%，每米波数为3，钢板坡度为65°；S2模型中覆盖宽度比为98%，每米波数为9，钢板坡度为90°。每组有限元模型中的板厚取值分别为0.6、0.9、1.2与1.5 mm。经分析计算得到3个方向的基本周期，计算结果如图8(a)所示，从中可以看出，3个方向的基本周期随板厚线性增大，板厚对结构基本周期的影响较为显著，如S1模型中板厚从0.6 mm增大至1.5 mm，UX方向基本周期从0.602 s增加至0.690 s，增大了14.7%。其主要原因在于板厚的增加使得结构自重增加，而刚度增加缓慢，从而使周期增加。

3.2 覆盖宽度比的影响分析

覆盖宽度比(η=a/l)描述了压型钢板的波折情况，覆盖宽度比越高，波折程度越小。，建立2组模型S1与S2，S1模型中板厚为0.6 mm，每米波数为3，钢板坡度为65°；S2模型中板厚为1.5 mm，每米波数为9，钢板坡度为90°。根据常用压型钢板型号，每组有限元模型中的覆盖宽度比分别取值为51%、66%、81%与98%。基本周期计算结果见图8(b)，3个方向周期随覆盖宽度比线性减小。同时，覆盖宽度比对结构基本周期的影响也较为显著，当S2模型中覆盖宽度比从51%增大至98%时，UX方向基本周期从0.690 s减小至0.604 s，减小了12.5%。其主要原因在于覆盖宽度比会影响围护板刚度，当覆盖宽度比增大时，质量显著下降，而X向刚度下降缓慢，Y向刚度略有升高，因此使得周期降低。

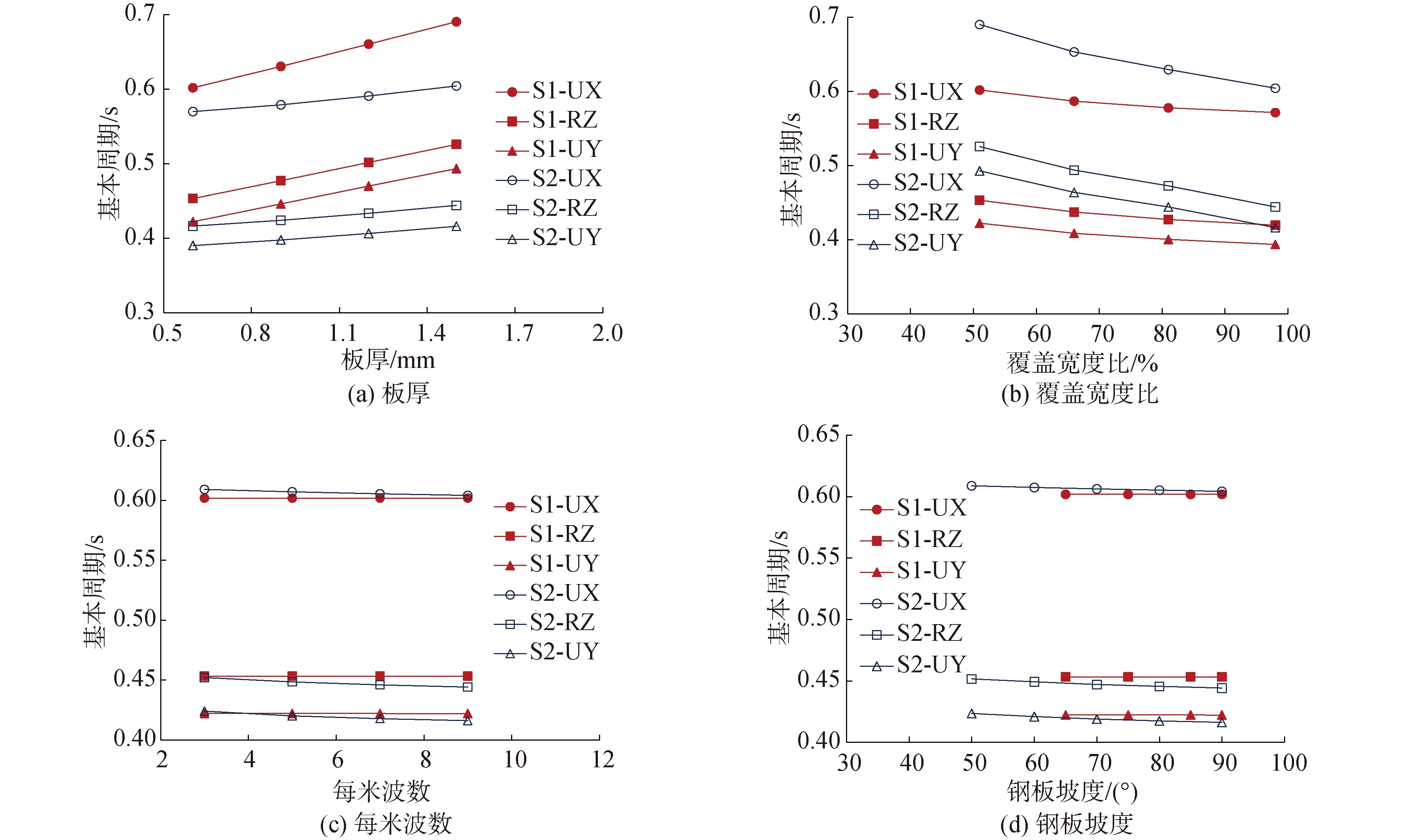
图8 压型钢板设计参数对结构基本周期的影响

3.3 每米波数的影响分析

每米波数指每米成型板折起波的组数，不同波数适用于不同的钢结构厂房建筑。建立2组有限元模型S1与S2，S1模型板厚为0.6 mm，覆盖宽度比为51%，钢板坡度为65°；S2模型中板厚为1.5 mm，覆盖宽度比为98%，钢板坡度为90°。有限元模型中每米波数分别取3、5、7与9。结构基本周期计算结果见图8(c)，从图中可以看出，每米波数对结构基本周期的影响较小，其影响可忽略。

3.4 钢板坡度的影响分析

钢板坡度是指压型钢板成型板波的斜坡与水平向的夹角。建立2组有限元模型S1与S2，S1模型板厚为0.6 mm，覆盖宽度比为51%，每米波数为3；S2模型板厚为1.5 mm，覆盖宽度比为98%，每米波数为9。模型S1中钢板坡度取值为65°、75°、85°与90°，模型S2中钢板坡度取值50°、60、70°、80°与90°(当S1取值50°时，无法形成压型钢板)。结构基本周期计算结果见图8(d)，可以看出，钢板坡度对结构基本周期的影响也较小，其影响可忽略。

4 单层钢结构工业厂房基本周期预测方法

4.1 理论分析

通过上文分析可知，钢结构厂房结构基本周期主要与围护结构板厚与覆盖宽度比有关。根据结构动力学可知，结构周期由结构刚度与质量确定，因此，可将简化模型厂房(M1)等效为一单自由度体系，其质量为m1，刚度为k1，如图9(a)所示。类似地，精细模型(M2)也可近似为一单自由度体系，围护结构质量为m2，其对厂房结构的刚度贡献为k2，如图9(b)所示。

图9 简化与精细化模型结构示意

因此，M1与M2的自振周期可分别表示为：

(6)

(7)

式中c1与c2为系数。

然而精细模型M2需要考虑大量围护结构构件及其约束关系，同时还需采用正交异性壳单元来模拟压型钢板，建模过程较为复杂，计算效率较低。因此，在实际设计计算过程中，可仍采用仅考虑主体结构构件的简化模型M1(图6(a))计算结构基本周期，在此基础上通过基本周期系数来计入围护结构的影响。为此，本文引入基本周期修正系数β，可表示为：

(8)

式中：刚度修正系数βk为k1/(k1+k2)；质量修正系数βm为m1/(m1+m2)。值得注意的是，此处周期可代表结构前三阶周期(UX、UY与RZ)。

4.2 实用简化公式

由式(8)可知，基本周期修正系数β主要由刚度修正系数(βk)与质量修正系数(βm)决定。而由图8可知，围护结构的板厚(t)和覆盖宽度比(η)对刚度与质量修正系数有影响，进而对周期修正系数产生影响。因此，本文采用最小二乘法对第3节参数化分析中选取的21个模型刚度与质量修正系数与围护结构设计参数(板厚与覆盖宽度比)进行拟合，如图11所示。拟合方程分别为：

βk=0.293 7+0.017 5η-0.014 7t

(9)

βm=0.825 8+0.228 9η-0.165 2t

(10)

拟合曲面的R2值分别为0.93与0.97，说明这2个参数可准确描述刚度与质量修正系数。进一步的，对周期修正系数与刚度和质量修正系数进行拟合，如图10所示。则式(8)可改写为：

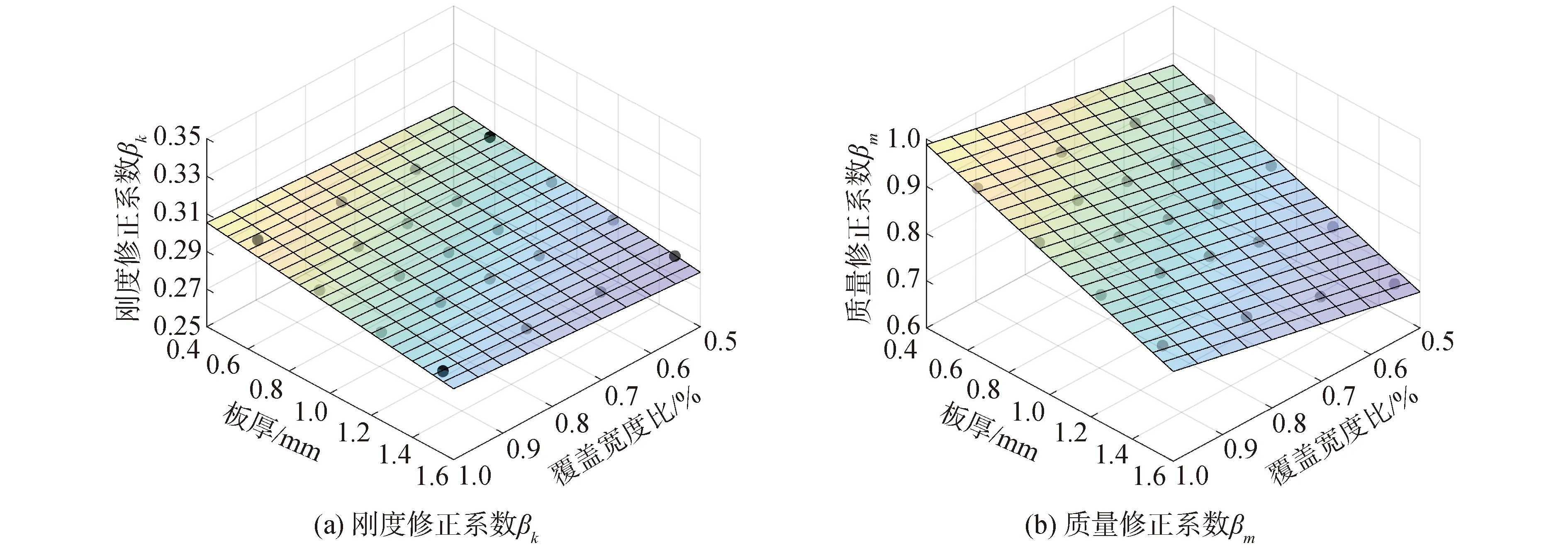
图10 修正系数βk、βm和板厚t、覆盖宽度比η的三维拟合平面

(11)

同时，对UY与RZ周期修正系数βUY、βRZ与UX方向βUX进行分析。图11给出了42种围护结构情况的βUX、βUY与βRZ的散点图，从中可看出，βUY、βRZ与βUX为明显的线性相关关系，由此可得：

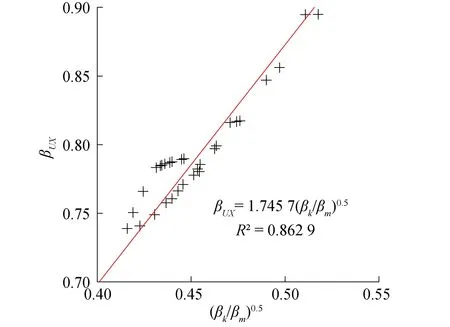
图11 修正系数βUX与βk和βm的相关性

βUY=1.069 5βUX

(12)

βRZ=0.746 6βUX

(13)

从图12可以看出，UY与RZ的拟合优度系数R2分别为0.95与0.94，接近于1，说明可采用式(12)和式(13)的过坐标原点的直线方程描述βUY和βRZ与βUX之间的关系。

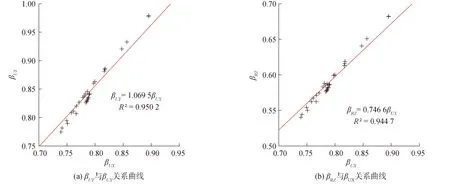
图12 βUY和βRZ、βUX的相关性

4.3 公式验证

为验证式(11)基本周期实用预测公式的可靠性，建立了4个单层钢结构工业厂房有限元模型T1～T4，如图13所示，模型T1横向共3跨，每跨跨度为24 m，纵向柱距为9 m，纵向总长为99 m；模型T2横向共2跨，每跨跨度为24 m，纵向柱距为9 m，纵向总长为135 m；模型T3横向共3跨，每跨跨度为24 m，减小纵向柱距至7.5 m，纵向总长为112.5 m；模型T4横向共3跨，减小每跨跨度至15 m，纵向柱距为9 m，纵向总长为135 m。T1～T4的横梁、柱、柱间支撑等主体结构构件与1.1节中的典型钢结构厂房一致。其围护结构考虑3种不同类型的压型钢板[25]，型号分别为YX130-300-600-0.8(B1)、YX28-100-800-0.8(B2)与YX35-125-750-0.8(B3)。

图13 验证结构有限元模型

首先，建立T1～T4的简化模型，计算得到各方向基本周期Ts；其次，将计算得到的Ts代入4.1节的基本周期实用预测公式，得到基本周期的公式预测值T；依据2.1节的建模策略，建立考虑围护结构的T1～T4的精细模型，计算得到各方向基本周期Tf如表5所示。采用式(16)与(17)分别计算简化模型的误差es和实用预测公式的误差e：

表5 验证模型的基本周期计算结果

(14)

(15)

图14给出了基本周期的计算误差结果。从中可以看出，简化模型计算得到基本周期与厂房的实际基本周期相差较大，最小误差超过20%，最大误差超过70%。而采用公式预测的基本周期误差大幅度减小，最大误差在6%左右。上述分析表明，本文提出的方法可根据简化模型计算结果较准确地预测大型钢结构工业厂房的实际基本周期，可为结构设计中的地震作用计算提供参考依据。

图14 基本周期计算误差

5 结论

1)简化模型计算得到的结构基本周期明显大于实测结果，且误差较大，而精细模型计算结果与实测结果吻合良好，说明围护结构对单层钢结构工业厂房结构刚度的贡献较为可观，在结构动力特性与地震作用计算中不可忽略。

2)结构基本周期随围护板板厚增加而增大，且表现为线性变化；压型钢板覆盖宽度比增大，结构基本周期则线性减小；每米波数及钢板坡度2个参数对结构基本周期的影响较小，可忽略其影响。

3)简化模型的基本周期与实际值相差甚远，难以直接用于动力特性计算和抗震设计，而实用预测公式的计算结果与实际值较为接近，最大误差在6%左右，本文方法可为大型钢结构厂房的结构动力计算分析提供参考依据。