基于分布式智能执行机构的航天器姿态协同控制

李文星， 吴云华， 朱翼， 许心怡， 陈志明， 华冰， 于丹

(南京航空航天大学 航天学院，江苏 南京 210016)

全球目前约有2 800多颗航天器在轨运行，其数量正在逐年迅速增加[1]，并且大部分航天器都有在轨维修和部件替换等需求。然而，航天器自诞生以来，其架构的设计理念基本没有发生变化：多个特定子系统通过通信及供电线缆连接组装成一个整体系统，由星载计算机进行统一管理，这种架构给卫星组装和在轨部件更换和升级带来了极大的挑战。因此，未来如何方便快捷地对航天器进行在轨维护成为一个亟待解决的问题。近年来，已有部分国家提出了一些航天器设计的新架构并将其付诸实际工程应用。其中，可实施性较强的发展方向主要为模块化可重构航天器设计，该架构航天器可由多个可替换模块组装而成，并且可以通过在轨模块替换实现航天器功能和性能的转变或者提升。近年来，各航天强国都着手模块化可重构航天器设计研究，例如美国DARPA的凤凰计划[2-3]，其计划对在轨废弃卫星的部件替换和回收利用。但在目前航天器设计架构下，如何在轨处理复杂的通信线缆对该计划能否顺利实施提出了质疑。2016年，国际空间站进行了“高度集成卫星”的组装实验[4]，由航天员手动组装了由6个模块组成的卫星，并进行了在轨投放实验，但是该构型航天器研制和组装十分复杂，实际上目前只能由航天员在轨组装实现，在轨投放之后难以通过在轨服务实现各个模块的替换和重构。因此，模块化可重构航天器实质上是在传统航天器设计架构上的进一步“改装”，对提升航天器未来在轨服务的便捷性意义较小。

针对上述问题，本文提出一种基于分布式智能部件的航天器新架构，该架构航天器由多种分布式智能部件构成，各分布式智能部件除供电线缆接口外无需其他通信线缆连接，各智能部件之间均通过无线网络进行通信，且智能部件均具有独立的处理器、存储器和数据通信能力，可以实现独立的数据处理、解算和输出，该架构航天器的优点在于各分布式部件具有独立调度和解算功能，并且各部件之间通过无线网络进行沟通协同，可以实现航天器去中心化，极大地减少了星上通信电缆，降低了航天器平台重量，同时也有利于航天器在轨部件替换等需求。

这种通过无线网络的闭环反馈控制系统可被称之为网络控制系统(network control system，NCS)[4-5]，该控制系统是一种空间分布的控制系统，系统内传感器、执行机构和控制器之间均通过无线通信网络交换信息。随着通信技术和计算技术的发展，NCS正逐渐大量应用于过程控制、遥操作和远程控制等诸多领域[6]。近年来，航天器系统设计领域也开始尝试采用无线网络控制系统方案，例如荷兰代尔夫特理工大学研制的Delfi-3卫星由于使用了超薄太阳电池片，为减少线缆排布等复杂设计，首次采用了无线太阳敏感器，建立并通过无线网络与星上其他组件进行数据传输[7]。但是，使用无线网络进行信息传输的同时也会带来信号传输时延等新问题。对提出的由分布式智能部件构成的航天器姿态控制系统而言，各个智能部件接收数据的传输时延差异会导致控制输出的不协调以及航天器姿态控制精度下降。因此，基于多分布式智能部件的航天器为实现高精度姿态控制，需要各分布式智能执行机构进行信息交换以进行协同控制。协同控制是保证多智能体系统能够进行有效配合工作的重要研究问题之一。协同控制在航天领域已经广泛应用于多航天器编队飞行等[8]。文献[9]针对有向拓扑通信结构的航天器编队，设计了一种基于反步法的协同控制算法，实现了多航天器对主航天器的姿态同步跟踪；文献[5]提出了一种分层控制策略，针对元胞空间分布式机器人设计了一种分布式控制分配算法，在不考虑中心节点的情况下，所提出的分布式控制分配算法可以实现与集中式算法相同的单元级优化分配。

本文所提出的基于分布式智能部件的航天器姿态协同控制实质上是一种多智能体—单平台协同输出问题。对于大部分的多智能系统而言，采用无线网络进行各智能体之间的数据通信是保证系统分布化与灵活性的重要手段，而采用无线网络进行数据传输就会不可避免地产生通信时延等问题[10]。为了保证多智能体在网络环境下的协同控制精度，必须针对时延问题进行解决。刘自理等[11]针对具有固定通信时延的多智能体系统，设计了一种分布式观测器对系统状态变量进行测量，但主要解决的是领导-跟随协同问题；Zhang等[12]针对时变时延通信的多智能体一致性问题进行了研究，但未考虑智能体在控制过程更新其他智能体状态的条件，对解决分布式多智能体系统输出协同问题作用有限；张薇等[13]提出了一种基于一致性理论的航天器飞行协同最优控制算法，但该算法依赖于网络时延量，并且其设计的控制算法复杂，为了保证控制器的有效性，对控制参数进行了严格限制，可实施性较差。

针对上述问题，以基于分布式智能部件的航天器姿态控制分系统为例，提出一种多分布式智能执行机构协同的航天器姿态控制方法。首先，提出一种自适应递阶饱和控制算法以保证多个分布式智能执行机构对航天器姿态的协同控制稳定性，随后基于一致性协同控制理论，设计分布式执行机构姿态协同控制律，并借助Lyapunov-Krasovskii理论证明其稳定性。最后，进行数学仿真和半物理仿真，通过仿真结果验证该算法的可行性。

1 基于分布式智能部件的GNC平台

由分布式智能部件构成的航天器分系统内各部件能够模仿自然界中智能体工作和协同机理实现各部件管理和协同。航天器平台不受星载计算机支配，突破航天器需要星载计算机对航天器平台进行集中管理的传统模式；其次，航天器平台分解成若干个功能独立的模块，各子系统能够独立自主地完成任务和协同工作；最后，系统内各部件之间通过无线传输进行数据交互，除了供电线缆之外，无需其他线缆进行连接。

如图1所示，以航天器姿态控制系统为例，分布式航天器姿态控制系统主要由分布式姿态确定子系统、分布式执行器子系统和无线组网管理子系统组成。姿态确定分系统确定航天器姿态，由智能敏感器组成；姿态控制分系统解算和输出控制力矩，由智能执行机构组成；无线组网管理分系统对各智能部件进行智能组网，选取组网管理中心，其中组网管理中心对任务指令进行接收、规划和发送。组网后，姿态确定分系统中，各智能敏感器向主敏感器发送姿态测量数据，主敏感器对姿态进行最优估计，并通过无线传输将单通道或多通道的带时间标签的姿态发送至各智能执行机构。姿态控制分系统中，各智能执行机构分别接收姿态信息，并根据预先存储的分布式姿态敏捷机动控制律进行控制指令解算，输出控制力矩。

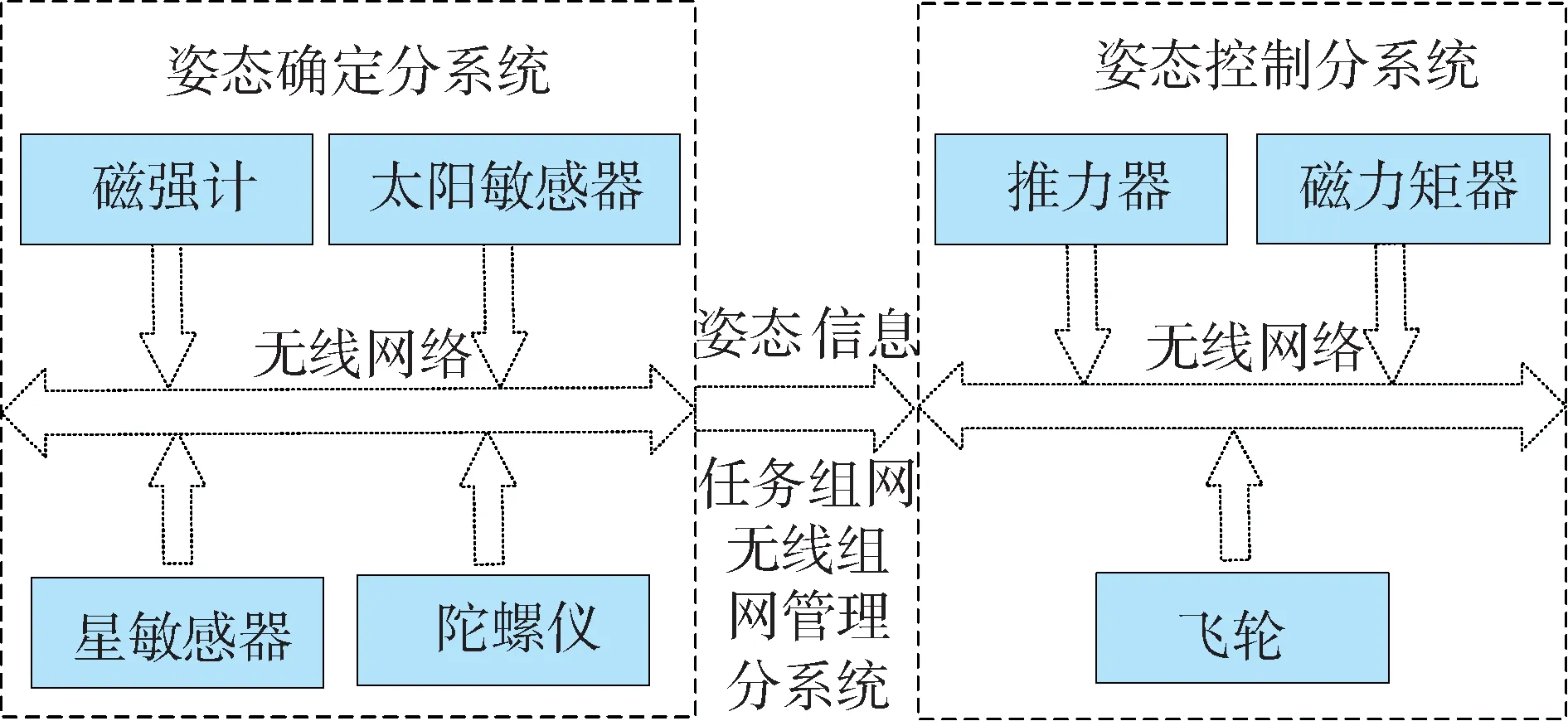
图1 分布式航天器姿态控制系统

各分布式智能部件除传统GNC系统部件功能模块外，还具有独立的处理器、存储器、无线传输模块和主要功能实现模块，如分布式智能星敏感器的主要功能模块为星载相机，分布式智能飞轮的主要功能模块为飞轮和电机。智能部件具有数据处理、时间同步、数据存储、任务调度、故障诊断、数据加密和无线传输等功能，上述功能无需星载计算机参与。

2 航天器姿态动力学与运动学模型

2.1 坐标系定义

地心惯性坐标系Ci:OXiYiZi，坐标系原点为地心，OXi轴指向春分点，OZi沿地球自转轴指向北，OYi在赤道平面内，可根据其他两轴使用右手法则确定。

航天器本体坐标系Cb:OXbYbZb，坐标系原点为航天器质心，三轴固连于航天器上，定义绕OXb轴旋转的姿态角为滚转角，绕OYb轴旋转的姿态角为俯仰角，绕OZb轴旋转的姿态角为偏航角。在理想情况下，OXb轴在轨道平面内指向运动方向，OYb轴与轨道平面法线方向平行，OZb轴指向地心，Cb为右手正交坐标系。

2.2 姿态动力学与运动学

采用姿态四元数Q描述航天器姿态：

(1)

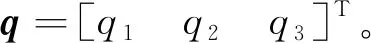
航天器姿态描述方程一般由姿态运动学方程和姿态动力学方程构成：

(2)

Jω=-ω×Jω+u+d

(3)

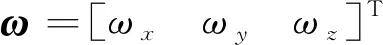
(4)

(5)

ω×表示为：

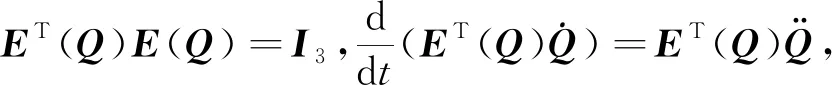
(6)

(7)

ωe=ω-ωd

(8)

(9)

2.3 基于分布式智能部件的航天器姿态控制模型

本文所描述的基于分布式智能执行机构的航天器姿态控制过程如图2所示，其姿态控制解算任务及控制力矩输出均由分布式智能执行机构实现。敏感器通过无线网络将航天器姿态信息分别发送至各执行机构，由各执行机构结合任务指令独立计算所需的控制力矩，则航天器姿态控制模型可重新表示为：

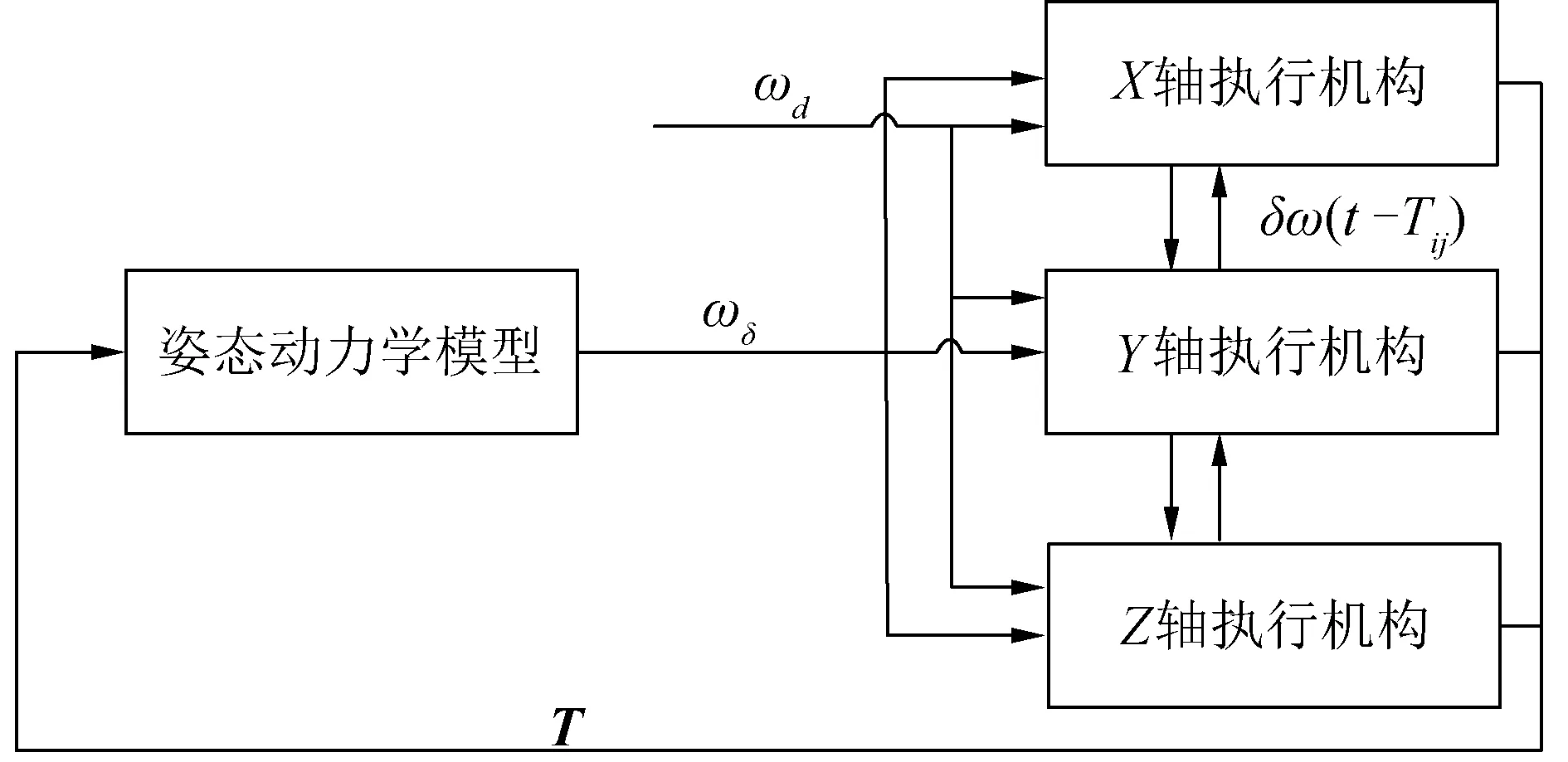
图2 分布式航天器姿态控制结构

(10)

(11)

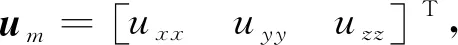
3 自适应姿态控制律

反作用飞轮、磁力矩器和冷气推力器等姿态控制执行机构都存在最大输出力矩上限。此外，受陀螺量程限制，航天器姿态机动角速度不能超过一定上限。假设航天器转动惯量已知，且姿态角速度可测量，姿态控制律为：

Tc=-Kqe-Dωe+ω×Jω

(12)

当K-1D非负时，控制律(12)对式(2)、(3)所描述的航天器姿态动力学和运动学方程全局渐近稳定，同时，参数K和D可以有下列4种形式：

1)K=kI,D=diag(d1,d2,d3);

4)K=[αJ+βI]-1，K-1D>0。

其中：k>0,I为单位矩阵，sgn为符号函数以及α,β>0，根据参考文献[14]，定义饱和函数：

(13)

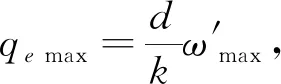
定义飞轮控制力矩饱和函数为：

(14)

式中Tmax为航天器执行机构最大输出力矩。

当t≥0，由式(2)和式(3)描述的闭环系统的解q(t)、ω(t)与q(0)是共线的，即在任意时刻航天器姿态机动都是关于q(0)的欧拉旋转。同时，考虑到分布式航天器部件具有即插即用及易替换性，该特性可能导致更换部件后的航天器转动惯量变化及转动惯量的不确定性，为了提高控制算法的鲁棒性，参考文献[15]设计自适应参数以实现对转动惯量J的在线辨识。因此，考虑航天器转动惯量的不确定性，基于分布式执行机构的自适应递阶饱和姿态控制律可表示为：

(15)

自适应项存在关系为：

(16)

(17)

Yi=H(ωir)+(ωir)×H(ωi)

(18)

定义线性变换矩阵H:R3×1→R3×6为：

4 基于分布式飞轮的姿态协同控制律

本节将协同控制理论和自适应递阶饱和控制算法相结合，设计自适应递阶饱和分布式姿态协同控制律。分布式部件协同控制系统如图2所示。首先，对本文所述的姿态控制系统做出假设：

2)航天器姿态信息由姿态敏感器测量得到并通过无线网络发送至各执行机构，并且不同执行机构接收信息的传输时延不相等，因此会导致不同执行机构进行控制指令解算时相互不协同；

3)各执行机构分别计算得到的姿态角速度误差ωei和姿态四元数误差qei通过无线网络发送至其他执行机构。设由执行机构i发送姿态误差信息至执行机构j的数据传输时延为Tij，考虑实际情况，不要求Tij=Tji。

4)假设所建立的无线网络环境稳定，则可认为数据传输时延Tij为常量。

设计姿态协同控制律为：

(19)

证明控制器的稳定性，设Lyapunov-Krasovskii函数为：

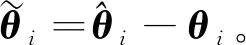
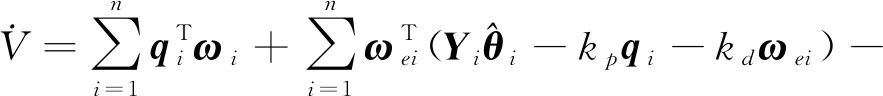
(20)

(21)

式中：

考虑到kij=kji，则有:

代入式(21)中，可以得到：

(22)

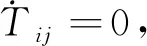
(23)

5 数学仿真及分析

为了验证基于分布式智能执行机构的姿态协同控制律的有效性，分别进行数学仿真和半物理仿真，数学仿真主要验证协同控制算法的有效性，并对采用协同控制算法和不采用协同控制算法进行对比分析，验证协同控制算法的有效性；半物理仿真验证在实际网络传输时延情况下，分布式智能执行机构协同姿态控制的可行性。

5.1 数值仿真

设航天器转动惯量为：

航天器初始角速度为[0 0 0]T(°)/s，初始姿态欧拉角为[40 -50 50]T(°)，目标姿态角速度为[0 0 0]T(°)/s，目标姿态欧拉角为[0 0 0]T(°)，设干扰力矩量级为10-4N·m，敏感器姿态角速度测量误差为10-3(°)/s量级，敏感器姿态角测量误差为10-4(°)量级，由姿态敏感器到各分布式智能执行机构的定常时延设置为：T1=0.05 s；T2=0.2 s;T3=0.1 s。

各分布式智能执行机构之间进行数据交换的网络传输时延设置为：T12=0.05 s；T21=0.08 s；T13=0.15 s；T31=0.12 s；T23=0.06 s；T32=0.1 s。

为了验证协同控制律的稳定性与有效性，对无协同控制项的自适应递阶饱和控制律和自适应递阶饱和协同控制律的仿真结果进行对比分析。为了描述方便，分别简称上述2种情况为无协同控制和协同控制，仿真条件设置相同如图3、4所示。

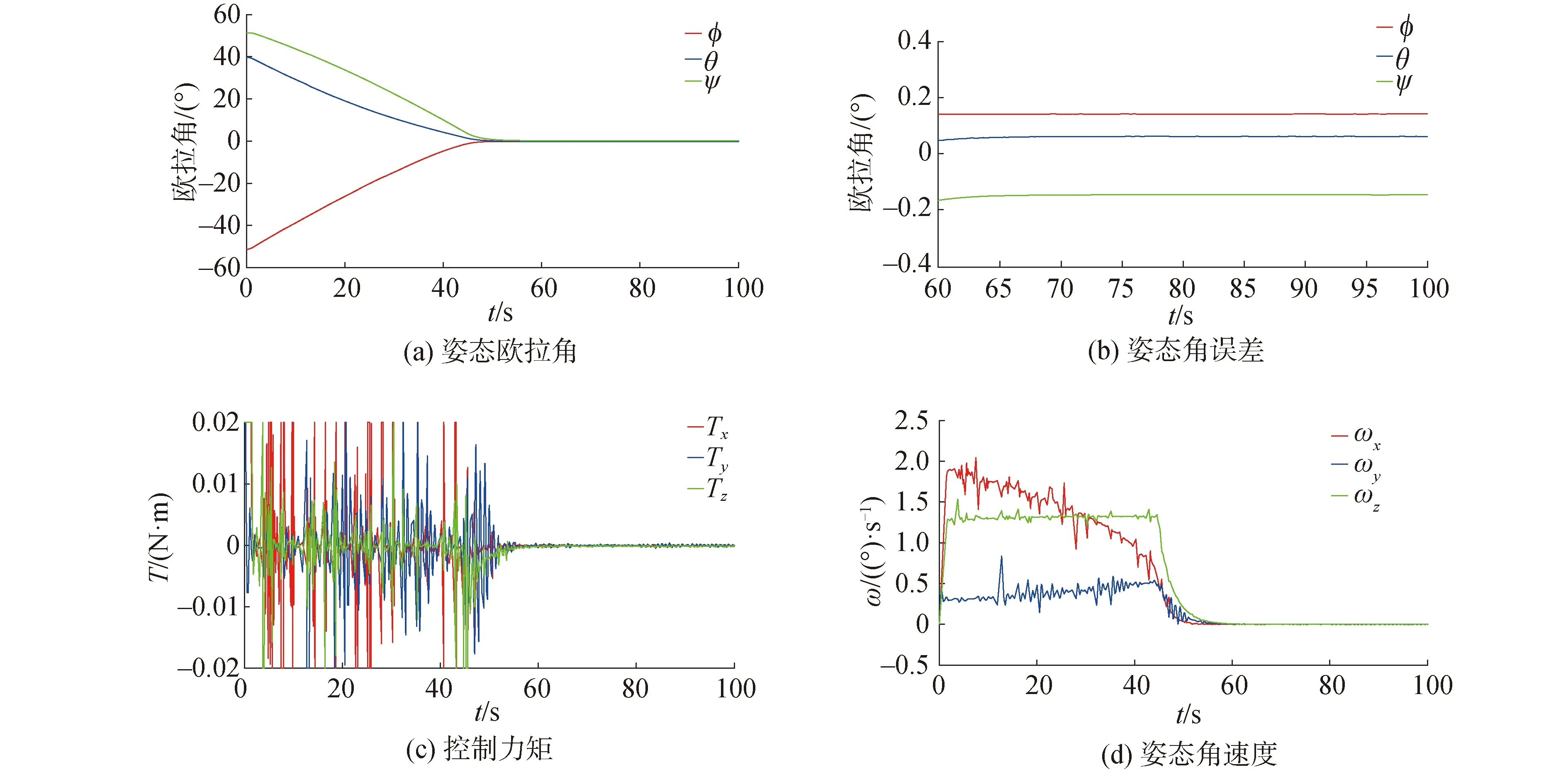
图3 无协同控制

同时，为了定量分析协同控制律是否能够保证各执行机构在控制过程中的输出力矩一致性，引入分布式智能执行机构输出力矩一致性指标函数：

显然，在控制过程中，分布式智能执行机构计算输出力矩相差越小，输出力矩一致性指标函数越接近于0，协同一致性越好。无协同控制和协同控制的输出力矩一致性指标如图5～6所示。

图4 分布式智能执行机构协同控制

图5 分布式执行机构输出力矩一致性(无协同)

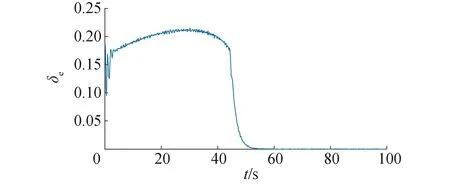
图6 分布式执行机构输出力矩一致性(协同控制)

综上，采用自适应递阶饱和分布式协同控制律能够更好地保持各执行机构输出力矩的一致性，验证了本文所提出自适应协同控制律的有效性。

5.2 半物理仿真

本仿真主要对自适应递阶饱和分布式协同控制律进行半物理仿真验证，验证在实际网络传输时延等情况下，协同控制律对基于分布式智能执行机构的航天器姿态协同控制的有效性。

分布式控制器采用NI-myRIO嵌入式计算机，半物理仿真平台使用LabVIEW-myRIO开发工具包进行部署应用，通过NI-myRIO的实时应用和内置Wi-Fi功能(2.4 GHz无线通信)实现远程部署应用，方便用于分布式智能执行机构的网络连接。

表1 数值仿真结果对比

半物理仿真结构如图7所示，使用分布式智能飞轮作为分布式智能执行机构，姿态控制系统采用3正交构型的分布式智能飞轮系统，设安装在x、y和z轴上的分布式智能飞轮分为1号、2号和3号智能飞轮。由于开发条件限制，其中1号智能飞轮为真实飞轮，2号和3号智能飞轮为虚拟飞轮。采用2台myRIO嵌入式计算机作为智能飞轮控制处理器：一台作为真实智能飞轮控制器，进行x轴真实飞轮的姿态控制解算、控制力矩计算、飞轮驱动控制、反馈真实飞轮输出力矩等任务；另外一台作为虚拟智能飞轮控制器，进行y、z轴虚拟飞轮的姿态控制解算、虚拟飞轮运行控制模拟等任务。虚拟智能飞轮和真实智能飞轮之间通过无线网络进行协同控制信息交互，虚拟智能飞轮之间直接交换协同信息，网络传输时延由数学模拟产生。

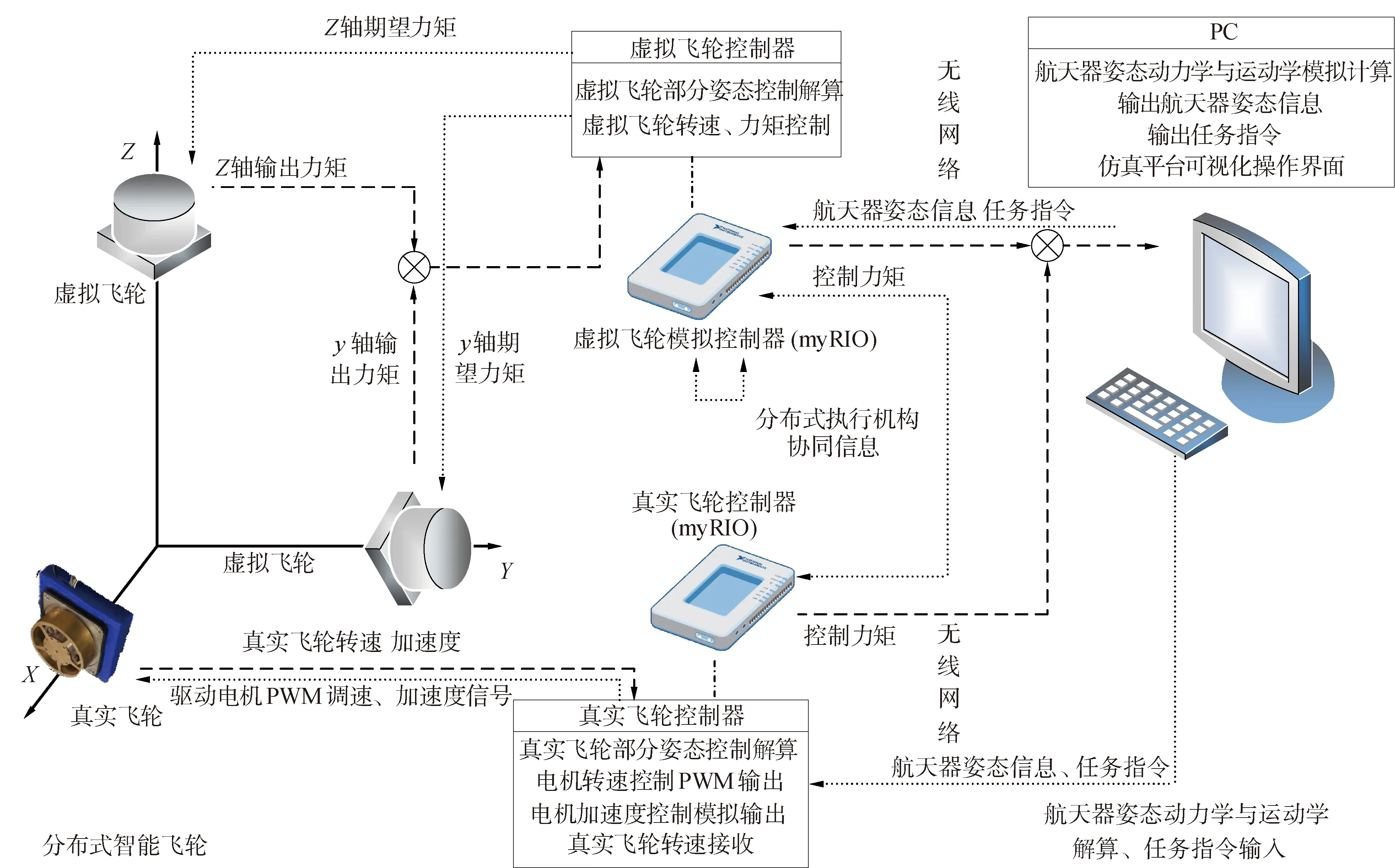
图7 半物理仿真结构

通过测量，半物理仿真平台各执行机构之间数据无线传输的通信时延在0.01～0.05 s，并且大部分时间维持在0.01 s左右，较少发生大的跳变。因此，在假设网络环境相对稳定的条件下，完全可以将时延看作常值。

对无协同控制和协同控制仿真结果进行对比分析，仿真结果如下图所示。

由半物理仿真结果图8～9可知，由于大时延的影响，分布式智能执行机构在输出控制力矩时会出现不协调的情况，导致输出力矩混乱，虽然航天器姿态也能够收敛至目标值附近，但是会出现0.3°左右的抖震现象；在采用协同控制算法之后，抖震现象明显消失，控制力矩输出及角速度也趋于平稳，证明了协同控制算法的有效性。

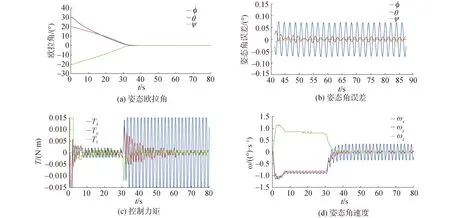
图8 无协同控制(半实物仿真)

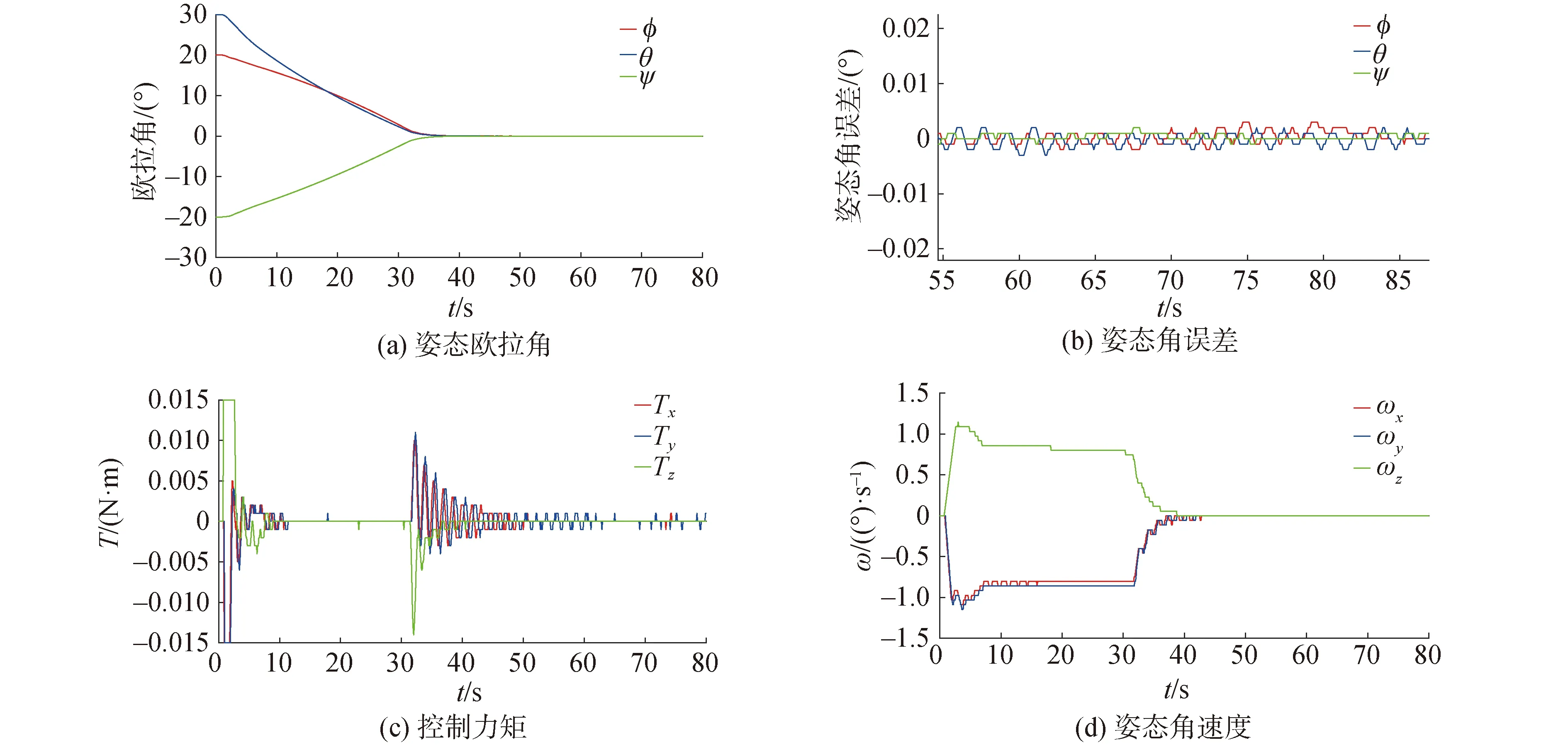
图9 分布式智能执行机构协同控制(半实物仿真)

表2 半物理仿真结果对比

6 结论

1)本文针对该系统数据传输存在时延等分布式特性，设计了一种基于分布式智能执行机构的航天器姿态协同控制算法，实现了分布式智能执行机构协同完成航天器姿态机动控制，解决了各智能飞轮之间存在数据传输时延、航天器参数不确定性以及存在干扰力矩等问题。

2)数值仿真和半物理仿真结果表明，所设计的自适应递阶饱和分布式协同姿态控制律能够在保证控制精度的同时有效解决网络传输时延所带来的分布式智能执行机构控制输出不协调性。

3)本文所提出的方法可以为未来采用分布式智能部件的航天器姿态控制提供理论基础。