速率模式飞轮姿态控制系统飞轮组合平稳切换方法*
李英波,陆 琳,张子龙,彭 瑞
(1.上海航天控制技术研究所·上海·201109;2.上海市空间智能控制技术重点实验室·上海·201109)
0 引 言
航天器姿态控制系统使用的飞轮有两种模式,一种是速率模式飞轮,另一种是力矩模式飞轮。顾名思义,速率模式飞轮输出的转速(或角动量)按一定关系(通常为比例关系)跟踪输入指令信号,而力矩模式飞轮的输出力矩(角动量变化率)按一定关系(通常为比例关系)跟踪输入信号。力矩飞轮也可通过星载计算机采样飞轮转速闭环而等效为速率模式以完成工作。
在以飞轮为执行机构的卫星姿态控制系统中,飞轮的配置往往存在一定的冗余,因此可以选择不同的飞轮组合进行卫星姿态的控制。当卫星上有大角动量扫描式有效载荷(如微波辐射计、微波散射计等)时,必须利用飞轮产生相反方向的角动量,将整星补偿为在轨道面内近似零动量,以避免出现过大的轨道陀螺力矩而对卫星的正常控制产生影响。为了尽可能减少飞轮的配置数量,控制系统可采用角动量补偿和姿态控制一体化方案。通常而言,扫描式有效载荷的角动量沿卫星偏航轴方向,在XOZ平面内的飞轮需同时兼顾角动量补偿和姿态控制两项功能。在扫描式载荷工作时,XOZ平面内参与角动量补偿和姿态控制的飞轮角动量有一定偏置,这种状态避免了由飞轮转速过零而造成的卫星姿态抖动。在扫描式载荷尚未工作时,可以适当增加参与工作的飞轮的数量,使其工作在速度偏置方式,避免由飞轮转速过零对卫星姿态带来抖动影响,并为星上其他载荷提供高稳定度的工作环境。这要求根据扫描载荷是否工作而主动采取不同的飞轮组合模式,保持卫星高姿态稳定度状态,本文第4节将对此进行实例分析。
在切换飞轮组合时,若不采取措施,退出和新参与控制的飞轮角动量会产生突变。此角动量突变将转移到卫星星体上,从而引起卫星姿态的抖动[1]。这种抖动会影响卫星有效载荷(特别是遥感载荷)的工作,造成卫星在短时间内性能下降,不能正常执行任务。
文献[2]对使用4个飞轮的“3正交+1斜装”构型和金字塔构型的飞轮组合的容错控制进行了研究,在1个飞轮失效或2个飞轮丧失部分输出能力的情况下,采用自适应容错非线性控制方案可以实现系统的容错控制,即可使系统在保持一定指向精度的前提下实现三轴稳定控制。文献[3]提出了自适应滑模容错姿态跟踪控制算法。当执行机构出现故障时,姿态偏离预定轨迹,触发滑模面的某些参数进行自适应调整,从而实现了容错控制。其原理是利用执行机构故障后的姿态偏离触发控制参数的自适应调整。因此,故障后的容错控制性能也发生了变化,但合理设计相关参数可以确保系统的渐进稳定性。文献[4]利用自适应多重估计器对故障参数进行了辨识并重构了系统,从而减小了飞轮在出现故障后对系统的影响。文献[5]利用估计器同时对故障类型和数值参数进行了估计,构建了自适应故障补偿器,对系统进行了反步闭环控制,从而减小了飞轮故障对跟踪过程的影响。文献[6-7]对四面体安装构型的飞轮组合和三正交经典安装构型的飞轮组合进行了比较,得出了四面体安装构型飞轮的能源利用率更高的结论。文献[8]对三种安装构型的使用性能进行了比较研究,这三种安装构型分别为3正交+1斜装、四面体构型和金字塔构型的飞轮组合。金字塔构型的飞轮组合在三轴上的加速度分配更为均匀。当一个飞轮完全失效后,金字塔构型飞轮组合的维持能力更强。文献[9]对应用于STUDSAT-2卫星的四面体安装构型的飞轮组合的力矩分配方式进行了研究,利用线性二次型调节器对某单一飞轮失效情况下的力矩分配进行了研究,得出了满足线性二次型约束的力矩分配矩阵。当系统使用的飞轮数量超过3个时,控制力矩在飞轮组合中的分配方式并非唯一。文献[10]对控制力矩在飞轮组合中的分配进行了研究,不但考虑了最大力矩的限制,还同时考虑了角动量约束。
目前,针对将飞轮作为执行机构的姿态控制系统的研究主要集中于对安装构型不同的飞轮组合的性能的比较,或某飞轮故障情况下的容错控制技术。在飞轮组合的某一个或两个飞轮出现部分故障时的容错控制虽然也涉及飞轮切换,但其属于被动切换,系统性能会发生某种程度的变化。目前,针对主动切换飞轮组合以适应不同载荷工作模式的高精度姿态控制技术的研究还很少。
本文对飞轮组合主动切换技术进行了研究。文中的速率模式飞轮包括了由力矩模式飞轮通过星载计算机采集飞轮转速而构成闭环的等效速率模式飞轮。本文在第1节给出了速率飞轮姿态控制系统的数学模型;在第2节对系统的能控性和飞轮组合切换过程进行了分析;在第3节提出了残余角动量卸载的飞轮组合平稳切换方案;在第4节分析了应用实例;在第5节对全文进行了简要的归纳和总结。
1 速率飞轮姿态控制系统模型
刚体卫星速率飞轮姿态控制系统的动力学模型如下式所示
(1)


(2)
(3)
式中,ω0为轨道角速度,L的定义如下

(4)
式中,K1=diag(k1φk1θk1ψ)。diag代表对角矩阵,对角元素k1φ,k1θ,k1ψ分别为滚动、俯仰、偏航通道的比例控制系数;K2=diag(k2φk2θk2ψ),对角元素k2φ,k2θ,k2ψ分别为滚动、俯仰、偏航通道的微分控制系数。
上式可写为
(5)
对于速率模式飞轮的控制系统,从测量环节衡量,其相当于PI控制器,可以省去用于测量角速度的陀螺组合。
将式(2)、式(3)、式(5)代入式(1),并略去2阶及以上小量,可得系统状态方程

(6)
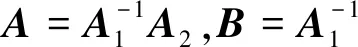
E3×3和03×3分别为3×3单位阵和3×3零矩阵,03×1为3×1零矩阵。
2 系统能控性和飞轮组合切换过程分析
对于参数确定的系统,通过合理设计控制参数矩阵K1、K2,可使式(6)描述的系统满足下式
rank([BAB…A5B])=6
(7)
即能控矩阵满秩,此时系统完全能控。
系统的稳定性由系统矩阵A的特征值决定。适当设计控制参数矩阵K1、K2,可以保证矩阵A的特征值具有负实部,系统稳定。
由式(5)得到的控制角动量要通过分配矩阵分配到各飞轮,飞轮组合再通过安装矩阵将其作用到卫星上,其转换过程如图1所示。系统的能控性由式(7)中的能控矩阵的秩确定,不受飞轮组合的影响。同理,系统的稳定性由式(6)中系统矩阵A的特征值是否具有负实部决定,也不随飞轮组合不同而发生变化。不同飞轮组合的角动量包络存在差异,这仅代表了飞轮组合的控制能力。
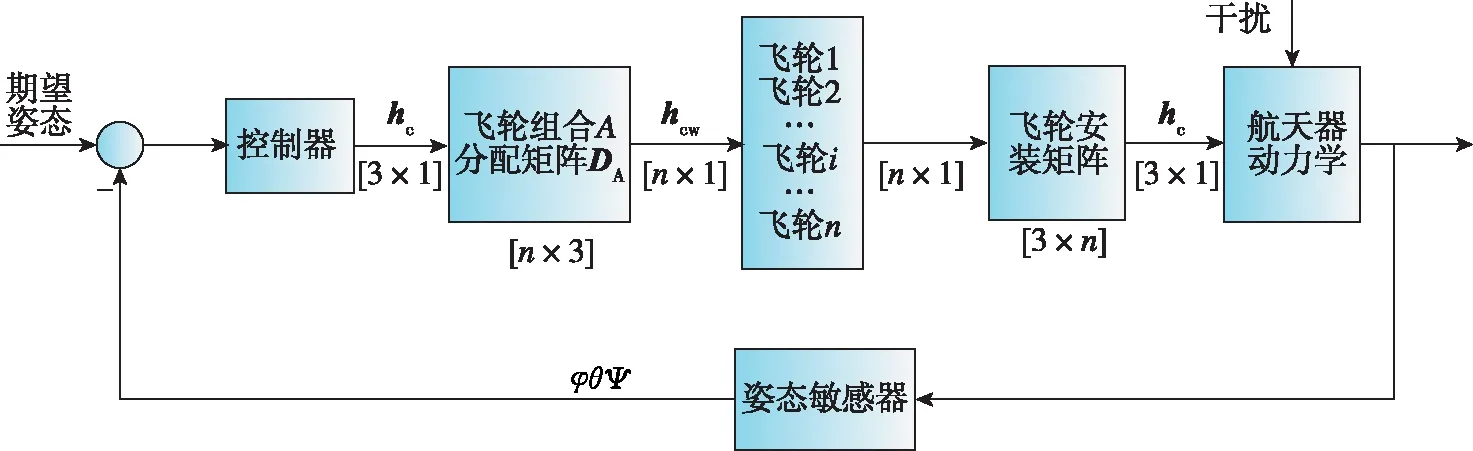
图1 飞轮组合A在工作状态下的系统框图Fig.1 Operating state of momentum wheels assembly A
不失一般性,设系统内有n台飞轮参与控制。由式(5)解算的控制量为沿卫星星体的三轴角动量hc=[hcx,hcy,hcz]T,此控制角动量[11-12]可通过飞轮组合的角动量分配矩阵[13](也称力矩分配矩阵,简称分配矩阵)D转换为飞轮组合的角动量
hcw=Dhc
(8)
式中,hcw=[hc1,hc2,…,hci,…,hcn]T为n台飞轮指令角动量,hc=[hcx,hcy,hcz]T为由控制器解算的三轴控制角动量,D为参与控制飞轮组合的分配矩阵,为n×3维,n(通常情况下,n=3~6)为参与控制的飞轮数量。若飞轮总数量为m(通常情况下,m=3~6),n≤m。其中,m-n为未参与控制的飞轮的数量。
假定在当前t0时刻参与控制的飞轮组合为{w1,w2,…,wi,…wn}(简称飞轮组合A),其分配矩阵为DA(DA为n×3矩阵,矩阵元素与飞轮安装的方向有关)。在t1时刻,切换为飞轮组合{w1,w2,…,wi-1,wi+1,…wn,wj}(简称飞轮组合B),其分配矩阵为DB。即第i个飞轮wi退出控制(i≤n),而代以第j个飞轮wj参与控制(j≤m),其他参与控制的飞轮不变。此时,飞轮分配矩阵为n×3矩阵。若只是第i个飞轮退出控制,没有新的飞轮加入控制,则有wj∉B。此时,飞轮分配矩阵为(n-1)×3。因此,飞轮组合切换后的分配矩阵及维数需视具体参与控制的飞轮组合而定。以下,以第i个飞轮退出,第j个飞轮加入的情况进行了分析。
设在飞轮组合切换的前一时刻,卫星的控制量为hc0=[hcx0,hcy0,hcz0]T,则各飞轮的指令角动量为
hcw0=DAhc0=[hc1,hc2,…,hci,…,hcn]T
(9)
其中,hcw0为n×1向量,代表原飞轮组合{w1,w2,…,wi,…wn}的指令角动量。
飞轮的实际角动量为hw0=[h1,h2,…,hi,…,hn]T。当卫星处于稳定运行期间时,hcw0≈hw0。在飞轮组合切换为{w1,w2,…,wi-1,wi+1,…wn,wj}后,设卫星的控制角动量变为hc1=hc0+Δhc=[hcx0,hcy0,hcz0]T+[Δhcx,Δhcy,Δhcz]T。其中,Δ表示小量,此控制量的前一部分对应切换前一时刻的控制量[hcx0,hcy0,hcz0]T,由飞轮组合{w1,w2,…,wi,…wn}承担。如式(9)所示,将飞轮组合A的指令角动量,写成如下形式
[hc1,hc2,…,hc(i-1),hci,hc(i+1),…,hcn]T
(10)
而[hcx0,hcy0,hcz0]T+[Δhcx,Δhcy,Δhcz]T由新的飞轮组合{w1,w2,…,wi-1,wi+1,…wn,wj}承担。同理,飞轮组合B的指令角动量为
高血压伴心力衰竭为目前临床中较为常见的一种心血管疾病,该疾病可损害患者的机体,且致死率较高,对患者正常的生活和生命安全均有严重影响存在。[1]针对高血压伴心力衰竭患者,不仅需要给予其合理的用药治疗,且需要加强临床护理干预力度。
(11)
对比式(10)和式(11)可以发现,两式存在如下区别:一是式(10)中存在hci项,而式(11)中的hci项则被换成了Δhcj;二是式(11)中的各项均增加了Δ项。Δ项是相对前一时刻的时间变化所对应的微小变化量,与是否进行了飞轮切换无关,对应系统不同时刻的相应状态,在分析飞轮组合切换时可不予考虑。由此可见,分析飞轮切换过程是否平稳,需要参考hci和Δhcj的处理方式,即如何处理退出飞轮和新参与飞轮的指令角动量,因其他飞轮的控制过程未发生变化。新参与的飞轮j的指令角动量为Δhcj。由于Δhcj是小量,飞轮j的控制与其他飞轮一样,控制状态是渐变的,不会引发系统角动量突变。飞轮i的指令角动量为hci,如果在切换后对飞轮i的指令角动量处理不当,就会引起角动量突变。例如,在飞轮组合切换后,为了让飞轮i尽快退出控制,需为飞轮的指令角动量赋0,这便会引起飞轮i的角动量突变。根据系统角动量守恒原理,此角动量突变会引发卫星本体的角动量突变,造成卫星姿态抖动,进而影响有效载荷的工作。如果飞轮i的角动量可一直保持在飞轮组合切换前的hci值,系统便不会产生角动量突变。飞轮i不参与控制,却一直维持着固定转速的运行,未起到使飞轮完全脱离工作状态的作用。如下所述,可以采用主动卸载策略,使飞轮i脱离工作状态,并保持系统的平稳工作。
3 飞轮残余角动量卸载及平稳切换
如前所述,如果在飞轮组合切换后,飞轮i退出控制但仍然保持了切换前一时刻的角动量,则卫星姿态不会发生抖动。这种假设的前提是飞轮i虽然不参与新的控制,但仍保持切换前的角动量不变。因此,平稳切换问题即转化成为了将退出控制飞轮i的残余角动量hwi平稳卸载的问题,这显然使得问题被简化了。要将飞轮i的角动量hwi平稳卸载,需根据卸载角动量和飞轮控制能力规划一卸载函数,为简单起见,可规划一线性函数
(12)
式中,t1为飞轮组合的切换时刻,hwi为飞轮i在切换前一时刻的实际角动量,因hci≈hwi,也可使用飞轮i在切换前一时刻的指令角动量hci。这样,飞轮i在tx时间内可将角动量卸载至0。因飞轮i已不参与系统控制,对其进行卸载同样会产生不期望的控制力矩,进而导致姿态卫星发生抖动。为了保持卫星姿态的稳定,需将此卸载角动量前馈到系统,以保持系统的姿态稳定,如图2所示。从角动量守恒原理来看,飞轮卸载力矩对卫星的作用,可通过前馈由飞轮组合B产生的控制力矩而加以抵消。tx的大小影响着卸载时间的长短,此值小则卸载力矩大。卸载时间不宜过短,在保证卸载力矩外,还要预留足够的控制能力,因此tx的取值应使卸载力矩占飞轮最大力矩的30%左右。

图2 飞轮组合B工作状态下的系统框图Fig.2 Operating state of momentum wheels assembly B
由对前述系统的能控性和稳定性的分析可知,引入残余角动量卸载并没有改变系统的状态方程(6),因此不影响系统的能控性和稳定性。引入残余角动量卸载,只是改变了飞轮组合和星体之间的角动量交换过程,使得残余角动量被其他飞轮吸收而没有作用到星体上,保证了星体的角动量不产生突变,因此在飞轮组合切换过程中保持了星体的高稳定度。
4 实例分析
4.1 某卫星飞轮配置及控制能力分析
图3示意了某卫星的有效载荷之一——微波辐射计在本体系Z轴方向产生的标称45Nms的扫描角动量。其控制系统采用了角动量补偿和姿态控制一体化方案,偏航轴斜装了2台68Nms的动量轮,斜装动量轮的正角动量方向在卫星本体坐标系的XOZ面内,分别偏向+X轴与-X轴方向,且与Z轴的夹角为α=10°,分别标识为飞轮Za和Zb。X轴配置了一台25Nms飞轮,称为飞轮X。俯仰轴的动量轮为卫星提供的标称-20Nms的偏置角动量,并对俯仰轴姿态实施了控制。1台工作飞轮,1台备份飞轮,分别为飞轮Ya和Yb。Y轴上的飞轮与XOZ平面上的飞轮的功能可相互独立。XOZ平面中的Za、Zb和X飞轮可同时兼顾角动量补偿和姿态控制的功能。在微波辐射计工作时,就XOZ平面飞轮而言,存在X-Za、X-Zb和Za-Zb三种组合模式。此时,无论是在哪种组合模式下,由于要补偿微波辐射计的扫描角动量,参与工作的飞轮均有相应的角动量偏置。飞轮的中心工作转速均不为0,其中心角动量与飞轮组合模式有关。X-Za模式下,飞轮X和飞轮Za的角动量分别为-7.8Nms和-45.6Nms;X-Zb模式下的飞轮X和飞轮Zb的角动量分别为7.8Nms和-45.6Nms;Za-Zb模式下的飞轮Za和飞轮Zb的角动量均为-22.8Nms。飞轮速度偏置,避免了飞轮工作在过零模式时,摩擦力矩突变对卫星稳定度的影响。当微波辐射计不工作时,在以上三种飞轮组合中,飞轮工作在过零模式,卫星的稳定度不利于星上其他有效载荷工作。为此,可以采用X-Za-Zb三个飞轮在一定偏置速度下的工作模式,如飞轮X中心角动量为7.8Nms,Za中心角动量为-22.8,飞轮Zb中心角动量为22.8Nms;或飞轮X中心角动量为-7.8Nms,Za中心角动量为22.8,飞轮Zb中心角动量为-22.8Nms。扫描载荷启动后,拟由哪个飞轮用于补偿和控制,便采用哪种角动量偏置,如此可实现最为简单的设计。比如,若载荷启旋后拟采用X-Za模式,则采用飞轮Za负偏置;若拟采用X-Zb模式,则飞轮Zb负偏置。在保证XOZ平面内近似零动量的同时,避免飞轮过零工作,有利于提高卫星的稳定度。因此,可以根据微波辐射计是否工作而主动切换不同的飞轮组合模式,以确保卫星的高稳定度控制。

图3 某卫星微波辐射计和飞轮配置示意图Fig.3 Layout of a microwave radiometer and momentum wheels of a satellite
如前所述,XOZ平面内的飞轮有四种基本工作组合,即X-Za、X-Zb、Za-Zb和X-Za-Zb组合,这四种组合模式的角动量包络如表1所示。角动量包络代表系统储存角动量的能力,包络越大,系统的抗扰能力越强,可控区域越大,飞轮的卸载次数越少。由表1可知,X-Za-Zb组合的包络最大,这是以飞轮数量为代价的。Za-Zb组合的包络最小,其对X轴的可控范围较小。

表1 四种组合模式的角动量包络Tab.1 Moment envelope of four assemblies
4.2 扫描载荷未工作时的飞轮切换
当扫描载荷尚未工作时,为提高卫星姿态稳定度,可采用3飞轮组合X-Za-Zb模式。该组合下的分配矩阵为
在6080秒时,微波辐射计起旋完成,将飞轮组合X-Za-Zb切换为X-Za组合,X-Za组合下的分配矩阵为
图4(a)为未采用飞轮残余角动量的卸载方案,飞轮Zb的指令角动量被赋予了0值,飞轮的角动量突变对卫星产生了扰动,从而导致卫星三轴姿态角速度均出现了不同程度的抖动,影响了卫星平台的姿态稳定度,如图4(b)所示。在采用角动量卸载方案时,可将飞轮Zb约为1.65Nms的角动量在100s内卸载到0值,如图5(a)所示。将卸载角动量乘以飞轮Zb安装矩阵列向量[-sinα0 cosα]T,并前馈到卫星滚动、俯仰、偏航轴,即将原三轴指令角动量扣除此前馈角动量后,再分配给切换后的飞轮组合。采用这种方式可实现飞轮组合的平稳切换,卫星三轴姿态角速度不会产生跳变,如图5(b)所示。

(a)飞轮角动量曲线

(a)飞轮角动量曲线
4.3 扫描载荷工作时的飞轮切换
当有效载荷工作时,设原工作飞轮组合为X-Za,则该组合下的分配矩阵为
在8000秒时,由原飞轮组合X-Za切换为X-Zb,则X-Zb组合下的分配矩阵为
在飞轮组合切换前,飞轮Za同时兼顾补偿有效载荷角动量和完成对Z轴的姿态控制的功能。其角动量较大,不采用卸载方案而进行飞轮组合切换,这不仅会使姿态角速度产生跳变,还有可能造成姿态失稳,如图6所示。图7(a)为采用了角动量的卸载方案,Za角动量约为-45Nms,可在1800秒内卸载到0。同时,可将卸载角动量乘以飞轮Za安装矩阵列向量[sinα0 cosα]T,并前馈到卫星滚动、俯仰、偏航轴,即将原三轴指令角动量扣除此前馈角动量后再分配给切换后的飞轮组合,姿态角速度不会产生跳变,如图7(b)所示。
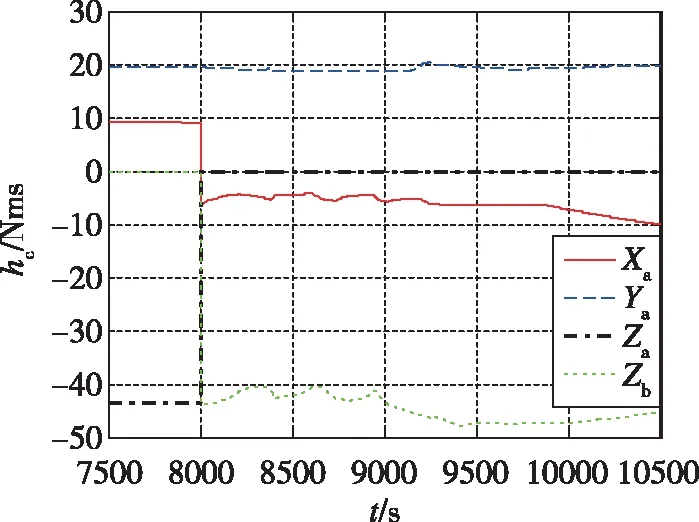
(a)飞轮角动量曲线

(a)飞轮角动量曲线
5 结 论
本文分析了速率模式飞轮控制系统的能控性和稳定性,给出了使用不同飞轮组合对系统进行控制不会改变原系统能控性和稳定性的结论。从飞轮组合的切换过程分析了飞轮组合与卫星之间角动量的交换机理,指出了导致卫星姿态抖动的影响因素,提出了基于飞轮残余角动量卸载的飞轮组合平稳切换方案。从系统能控性和稳定性分析得出了采用残余角动量卸载方案在保持卫星姿态平稳的同时,并不影响原设计系统的能控性和稳定性的结论。通过应用实例给出了卫星在几种典型飞轮组合间切换的过程,说明了所提出的飞轮组合平稳切换方法的有效性。

