火星大气电离层穿刺探测飞行动力学与轨迹优化

李明儒， 徐聪， 齐征， 赵爱红， 吴限德， 王剑颖

(1.中山大学 航空航天学院，广东 广州 510275； 2.北京临近空间飞行器系统工程研究所， 北京 100076； 3.哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001)

火星是太阳系中离地球最近的一颗类地行星，因此它一直是人类行星探测的首选目标。火星探测对于人类认识和了解类地行星的演化过程、气候变化的成因以及探索生命的起源都具有重大的参考价值[1]。关于火星探测的诸多方面中，火星大气电离层是必须了解的火星电磁环境，因为其直接关系到地球与火星之间的通信、火星当地的通信等重要活动[2]。除此之外，研究火星大气电离层对于利用雷达在火星上找水源是极其重要的，因此火星大气电离层探测研究具有重要的理论意义和工程价值。

火星大气电离层探测的方式大致可分为直接探测和间接探测2种。直接探测是采用空间飞行器作为载体，将探测装置携带到电离层中对其进行直接测量；间接探测是采用人工发射机发射的电磁波，经过电离层传播时与等离子体相互作用产生电磁效应，进而间接地推算出电离层特性参量。但直接探测存在观测时间短、探测区域片面等问题；间接探测则空间分辨率低，无法探测到火星电离层中的精细结构，且可探测的电离层太阳天顶角范围受到地球与火星轨道的限制。

针对上述探测方式存在的不足，本文提出一种基于升力体飞行器的穿刺探测方法。该方法采用升力体飞行器作为载体，依靠气动力在火星大气层内外往复穿刺飞行，实现对电离层的探测，同时采用气动力辅助变轨的思想，改变穿刺探测飞行轨道，实现对火星大气层全方位的探测，为获得稳定、全面且准确的探测数据提供支撑。20世纪60年代，London[3]在关于变轨问题的论文中提出了气动力辅助变轨的概念。随后国外有许多学者对气动捕获进行了研究，Cruz[4]提出了气动捕获任务设计的概念。French等[5]提出了将气动捕获用于行星际探测任务。Vaughan等[6]研究了火星气动捕获过程的轨道特性。近些年我国也有相关人员对此问题进行了研究，符俊等[7]针对共面椭圆轨道转移问题，采用Gauss伪谱法进行了气动力辅助最优转移研究。姬聪云等[8]针对微小卫星在变轨问题中的难点，采用Gauss伪谱法进行了微小卫星气动力辅助变轨研究。唐青原等[9]针对火星大气密度低、大气不确定性强等问题，采用基于预测校正制导的组合式制导方法进行了火星气动捕获制导研究。上述文献大多关注于飞行器穿越一次大气层进行轨道改变的问题，虽然也有部分文献提到飞行器多次穿越大气层进行变轨，但是其变轨目标和被控对象均与本文研究的对象不同，因此无法直接应用于穿刺探测飞行。

针对火星大气电离层穿刺探测飞行的动力学建模与轨迹优化问题，本文首先基于升力体飞行器的气动辅助变轨特性，提出多次改变近地点幅角的穿刺探测飞行任务模式；其次，建立升力体飞行器穿刺探测的动力学模型，通过联立轨道动力学方程与弹道动力学方程，推导弹道参数与轨道六根数间的转换关系，获取大气层内外的飞行动力学。进一步，采用Guass伪谱法进行轨迹优化，给出多次改变近地点幅角飞行轨迹的目标函数、优化变量和约束条件等。最后，通过数学仿真验证本文方法的有效性。

1 多次改变近地点幅角的穿刺探测飞行任务描述

考虑升力体滑翔飞行器对火星大气层采用“再入点进入大气——气动辅助变轨——弹出大气进入新轨道”的往复穿刺探测飞行模式，如图1所示。每次进入火星大气层时，利用大气层内飞行段进行电离层探测，同时利用气动力改变飞出大气层入轨点的参数，使得轨道近地点幅角发生改变，轨道相位进行旋转，从而保证再次进入大气层时，能够对不同区域的电离层进行探测。该穿刺飞行模式能够保证飞行器在有限次进入大气层的情况下完成对火星半球的电离层探测，因为火星大气具有对称性，因此可以实现火星大气电离层的完整探测。同时飞行器在穿刺探测后仍然能够进入空间轨道，保证了信息传输的有效渠道。

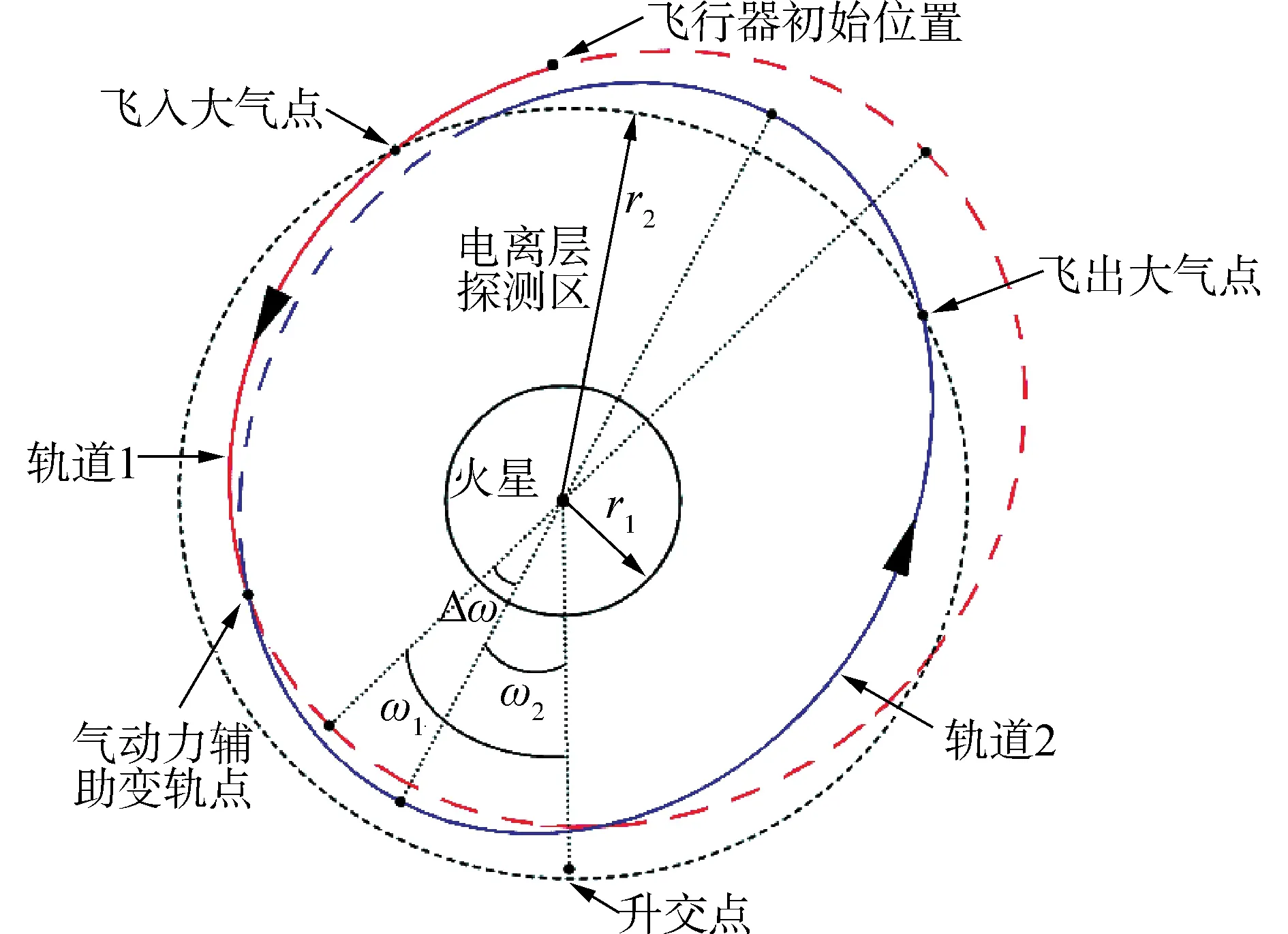
图1 穿刺探测示意

根据穿刺探测飞行任务，升力体飞行器需要在火星大气层内外进行多次穿刺飞行，利用气动力改变近地点幅角进而实现不同区域的探测。为了实现对火星大气的全方位探测，考虑到火星大气的对称性，多次穿刺飞行的近地点幅角改变量不少于180°。

2 穿刺探测飞行动力学模型

2.1 大气层内外动力学模型

考虑升力体滑翔飞行器在火星大气内外穿刺飞行的过程中，飞行器仅依靠气动力在火星大气层内进行滑翔飞行，所以飞行器主要受到空气动力及火星与飞行器间的万有引力作用。此外，本文分析中不考虑火星自转。根据该假设可以得到飞行器大气层内无动力三自由度再入运动方程为[10]：

(1)

(2)

(3)

(4)

(5)

(6)

式中：r、θ、φ分别为火心距、经度、纬度；v、γ、ψ分别为飞行器的速度、速度倾角、速度偏角；m、S分别为飞行器的质量、有效截面积；g、ρ、α分别为重力加速度、火星大气密度、攻角；D、L分别为阻力、升力。

火心距r、经度θ和纬度φ这3个位置参数在火心球面固连坐标系中描述。速度参数由速度大小v、速度倾角γ和速度偏角ψ确定。运动参数在图2表示，图中O-XYZ为火心固连坐标系，O-xyz为飞行器位置坐标系[11]。

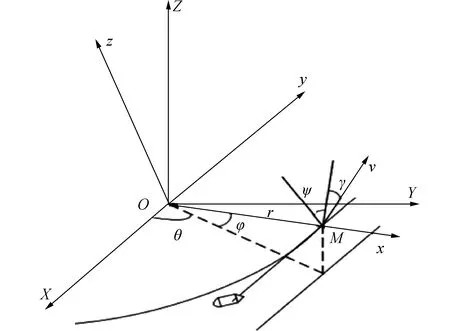
图2 运动参数示意

当飞行器飞出火星大气层后，大气密度为0，飞行器的升力和阻力也随即消失，即式(4)和(5)中的D和L分别等于0。

2.2 弹道参数与轨道参数转换关系

对火星大气电离层进行穿刺探测，飞行器需要在火星大气层内外往复飞行，是一个涉及弹道参数、轨道六根数以及其相互转换的问题，本节通过联立方程建立弹道参数与轨道六根数间的转换关系。

2.2.1 由弹道参数转换轨道参数

已知弹道参数，根据式(7)和式(8)可求得半长轴a和偏心率e[12]：

(7)

(8)

(9)

式中μ为火星引力常数。

由式(9)可知：

(10)

h=rvcosγ

(11)

(12)

将式(11)代入式(12)，可得：

(13)

将式(13)代入式(10)，有：

(14)

因此由式(14)可得真近点角f为：

(15)

根据图3中的球面几何关系，可得轨道倾角i为：

i=arccos(cosφsinψ)

(16)

另有：

(17)

因此由式(17)可得升交点赤经Ω为：

(18)

根据图3中的球面几何关系，还可知：

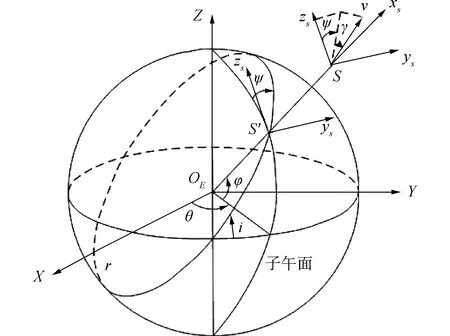
图3 惯性坐标系与球坐标系

(19)

(20)

因此由式(15)和式(20)可得近地点幅角ω为：

(21)

2.2.2 由轨道参数转换弹道参数

已知轨道六根数，根据轨道方程和活力公式，可以求得火心距r和速度v[12]:

(22)

(23)

由偏心率e和真近点角f可得速度倾角γ为：

(24)

根据图3中的球面几何关系，可得纬度φ为：

φ=arcsin(sinisin(f+ω))

(25)

(26)

因此，由式(26)可得经度θ为：

(27)

又有：

(28)

因此，由式(28)可得速度偏角ψ为：

(29)

3 基于Gauss伪谱法的穿刺探测轨迹优化方法

3.1 目标函数

要想实现对火星大气电离层的完整探测，升力体飞行器需要在火星大气层内外多次往复穿刺飞行。因此，飞行器所具有的能量是决定其能否完成多次穿刺飞行的关键，所以，再入轨迹优化的一个重要目标就是使飞行器每次飞出大气层时的速度达到最大，即性能指标函数为：

J=-vf

(30)

式中vf代表飞行器每次飞出大气层时的速度。

3.2 优化变量

优化变量如何选取是本文重点研究的内容之一。首先，推导近地点幅角方程，得到近地点幅角和弹道参数的关系。随后，进行参数敏感性分析，将对近地点幅角敏感度最大的参数选为优化变量。

3.2.1 近地点幅角方程

根据穿刺探测飞行任务，飞行器需要在火星大气层内外进行6次穿刺飞行，利用气动力改变近地点幅角进而实现不同区域的探测。因此，如何设计穿刺探测中大气层内飞行的终端条件十分重要。为分析设计该终端条件，首先构建近地点幅角方程：

将式(14)代入式(15)中可得：

(31)

将式(19)代入式(20)中可得：

(32)

将式(16)代入式(31)中可得：

(33)

将式(31)和式(33)代入式(21)中，可以得近地点幅角ω关于弹道参数的关系式：

(34)

由式(34)可以看出，近地点幅角ω与火心距r、纬度φ、速度v、速度倾角γ以及速度偏角ψ5个弹道参数相关，并且与火心距r、纬度φ、速度偏角ψ、速度v的平方以及速度倾角γ的平方是反三角函数的关系。因此需要进一步分析近地点幅角ω局部灵敏度，以明确优化设计目标。

3.2.2 参数敏感性分析

由前一节分析可知，近地点幅角的优化是一个涉及多变量优化的问题[13]。为了开展优化工作，采用直接求导法对近地点幅角进行局部灵敏度分析。

1)近地点幅角ω对纬度φ的敏感度：

(35)

2)近地点幅角ω对速度偏角ψ的敏感度：

(36)

3)近地点幅角ω对速度v的敏感度：

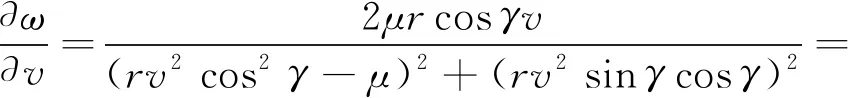
(37)

4)近地点幅角ω对速度倾角γ的敏感度：

(38)

在一定的弹道参数范围内，并在同一量度下分析参数敏感度，具体分析结果如下。

从图4～7中可以看出，近地点幅角ω对速度倾角γ求偏导的最大值是18.318 3，对纬度φ求偏导的最大值是11.544 3，对速度偏角ψ求偏导的最大值是11.505，对速度v求偏导的最大值是0.016 560 9。因此，速度倾角γ对近地点幅角ω的影响最大，所以将其设为优化变量。

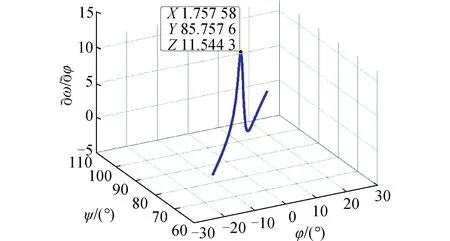
图4 近地点幅角ω对纬度φ的敏感度

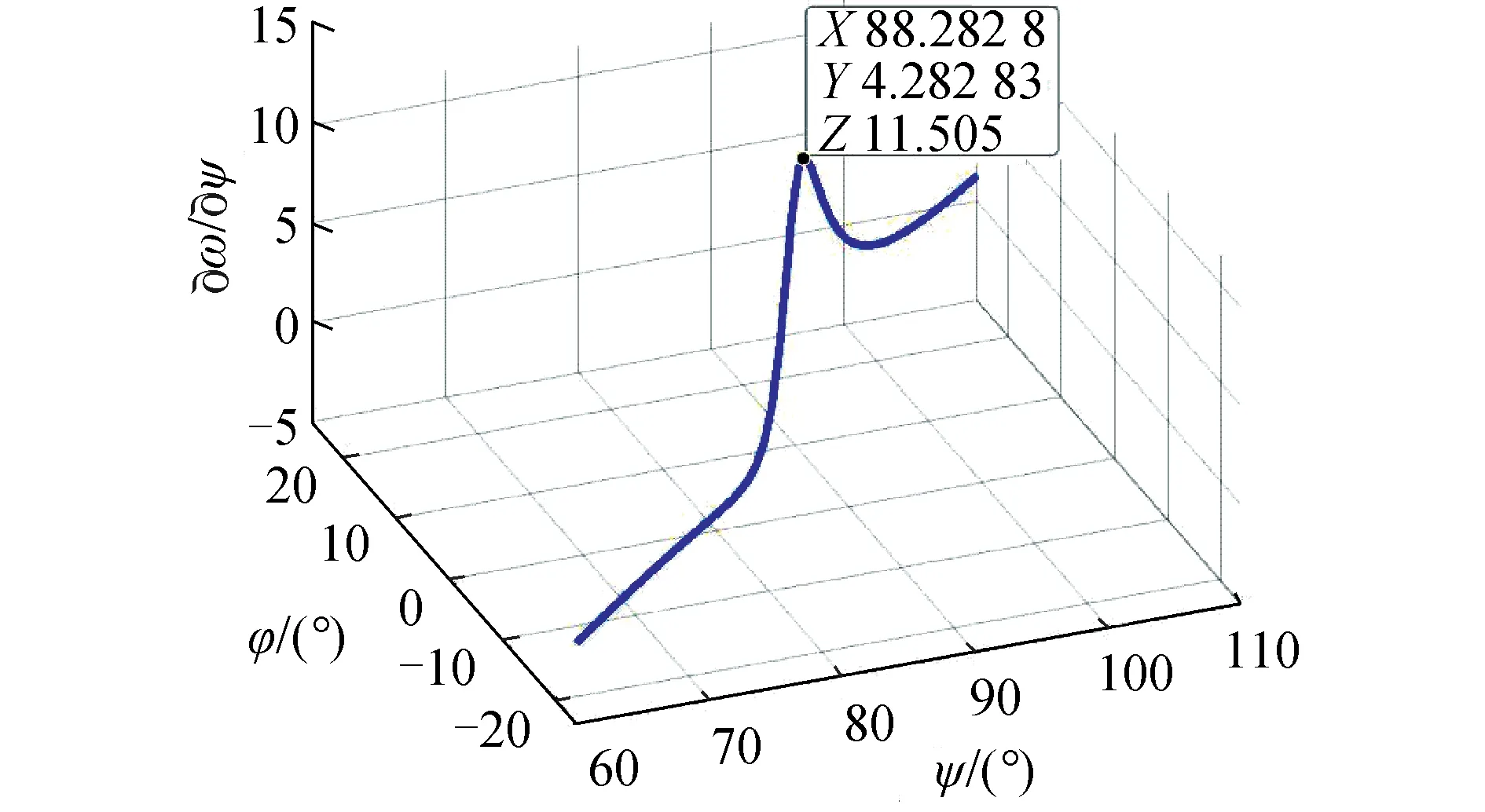
图5 近地点幅角ω对速度偏角ψ的敏感度

3.3 约束条件

根据穿刺探测共面轨道的约束，采用固定变量法分析建立终端状态约束条件，具体建立过程为：

i=arccos(cosφsinψ)

(39)

(40)

由式(40)可以看出，当穿刺探测轨道的倾角i确定后，飞出点的速度偏角ψ只与纬度φ有关。

(41)

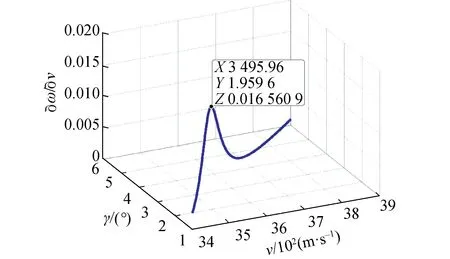
图6 近地点幅角ω对速度v的敏感度

图7 近地点幅角ω对速度倾角γ的敏感度

根据式(39)可以求出cosψ的表达式：

(42)

将式(42)代入式(41)中，可得：

(43)

由式(43)可以看出，当穿刺探测轨道的升交点赤经Ω确定后，飞出点的经度θ只与纬度φ有关。

(44)

(45)

将式(42)代入式(45)中可得：

(46)

由上面的分析可以看出，当飞出点的火心距r、轨道倾角i以及近地点幅角ω确定后，选定飞出点的纬度φ，经度θ和速度偏角ψ均能唯一确定，即终端位置确定，并且飞出点的速度v只与速度倾角γ有关。

至此，轨迹优化问题的完整模型可以根据上述分析确定，通过选定不同的飞出点纬度φ，明确飞行器飞出大气层时的位置，即确定终端状态约束条件，同时，将速度倾角γ设为优化变量，飞出点的速度vf设为优化目标，即可对穿刺探测飞行轨迹进行优化。

3.4 基于Gauss伪谱法的穿刺探测轨迹优化方法

Gauss伪谱法采用Legendre多项式的根作为离散点，并将控制变量以及状态变量同时离散化，进而将弹道优化的最优控制问题转化成非线性规划问题进行求解。

设最优控制问题的时间区间为[t0,tf]，采用Gauss伪谱法则需将时间区间转换到[-1, 1]，因此对时间变量t作变换：

(47)

Gauss伪谱法的离散点为N阶Legendre多项式的根，Legendre多项式为：

(48)

Legendre-Gauss点分布在区间(-1, 1)，增加τ0=-1，得到区间[-1, 1)，共N+1个插值点。以Lagrange插值多项式作为基函数描述控制变量以及状态变量：

(49)

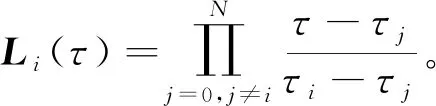
状态变量的一阶微分可以通过对式(49)求导来近似得到，同时将动力学微分方程约束转化为代数约束。

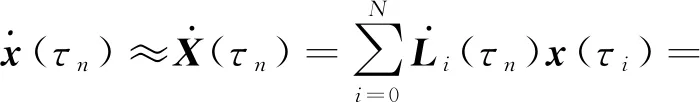
(50)

所以动力学方程满足：

(51)

式中n=1,2,…,N。

终端状态Xf可通过拉格朗日积分得到：

U(τn),τn;t0,tf]

(52)

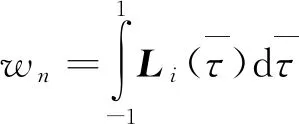
Gauss伪谱法中的性能指标函数为：

(53)

将连续系统离散化之后，最优控制问题转换成非线性规划问题，再利用序列二次规划算法进行寻优，即可得到需要的再入轨迹。

4 数学仿真及结果分析

本节基于Gauss伪谱法优化理论[14-18]对所构建的动力学模型以及参数关系进行仿真验证，具体仿真参数以及仿真结果如表1。

表1 火星环境参数和飞行器参数

另外，火星大气层十分稀薄，大气密度不到地球的1%，本文认为火星大气高度在高于100 km后不受大气影响。

飞行器的初始轨道六根数以及弹道参数如表2所示。

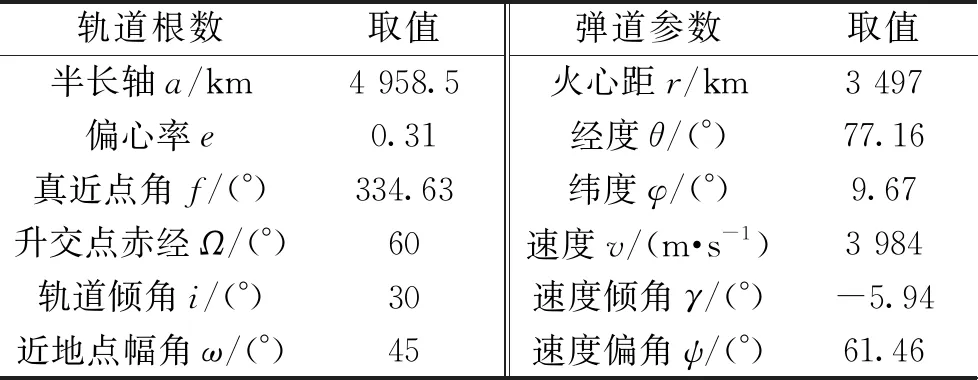
表2 初始轨道六根数以及弹道参数

表2中，初始轨道的远火点选择在火星大气层外，且半径为ra=6.5×106m，近火点选择在大气层内，且半径为rp=3.427×106m，飞行器的真近点角选择为刚进入火星大气层时的位置，且真近点角为f=334.63°，火心距r=3 496 996.38 m。

为了实现对火星大气全方位探测，本文设置升力体飞行器6次穿越大气，每次近地点幅角改变量不小于30°，近地点幅角总改变量不小于180°。通过本文构建的动力学模型以及参数方程，进行仿真分析，具体仿真图像如图8～13所示。

图8 穿刺探测飞行轨道

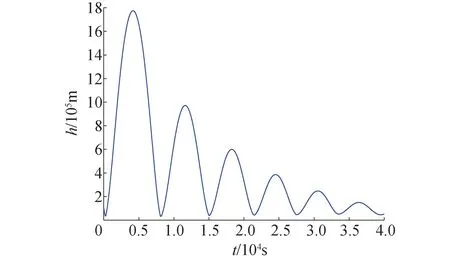
图9 高度h与时间t的关系

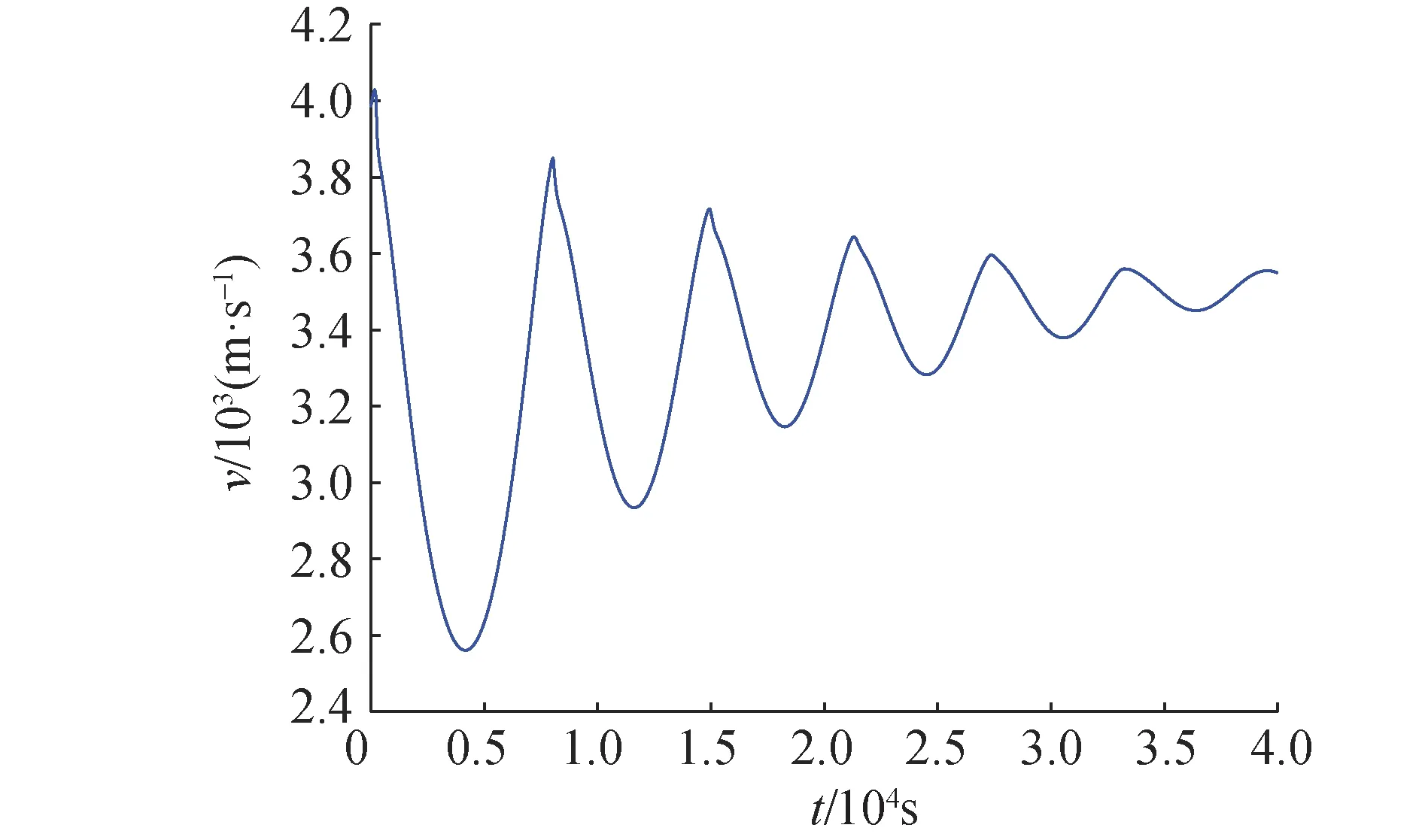
图10 速度v与时间t的关系

图11 速度倾角γ与时间t的关系

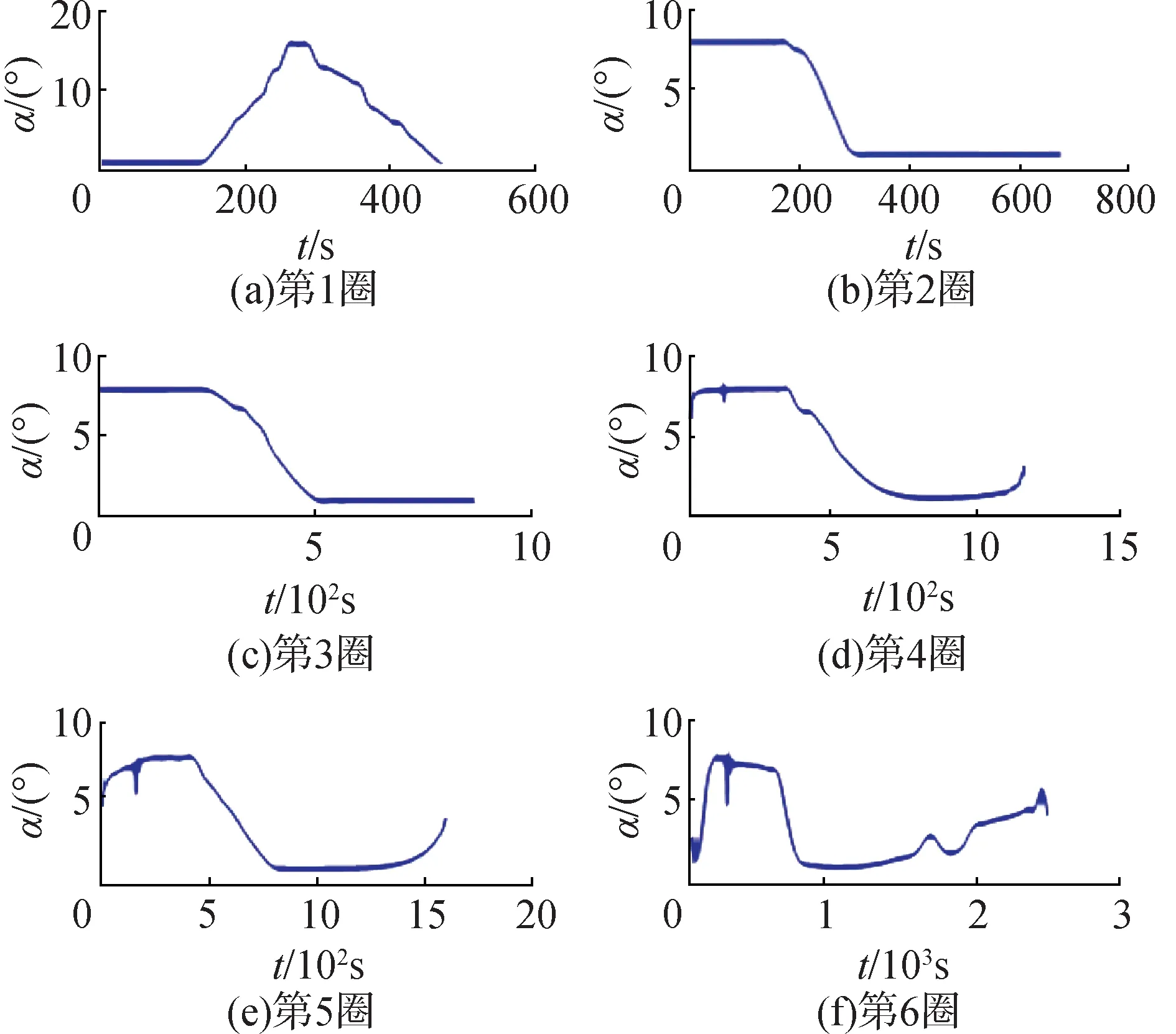
图12 攻角α与时间t的关系

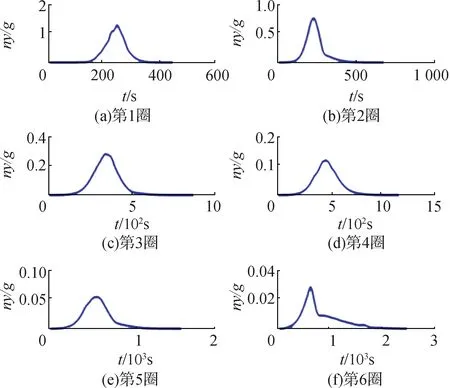
图13 法向过载ny与时间t的关系

结合表3和4能看出，飞行器完成了火星大气层内外6次穿刺探测飞行。此外，飞行器能在火星大气层内长时间无动力滑翔飞行，每次探测轨道的近火点半径以及近地点幅角均会发生改变，且6次穿刺探测飞行近地点幅角的改变量均不低于30°，近地点幅角总共改变了190.4°，再根据火星大气的对称性，因此可以实现火星大气电离层的完整探测。

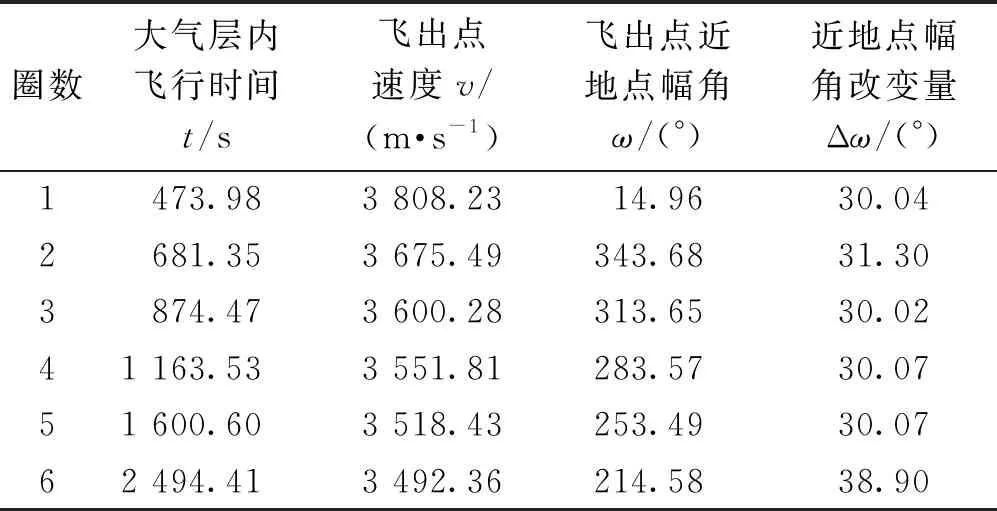
表3 基于Gauss伪谱法穿刺飞行轨迹优化仿真结果

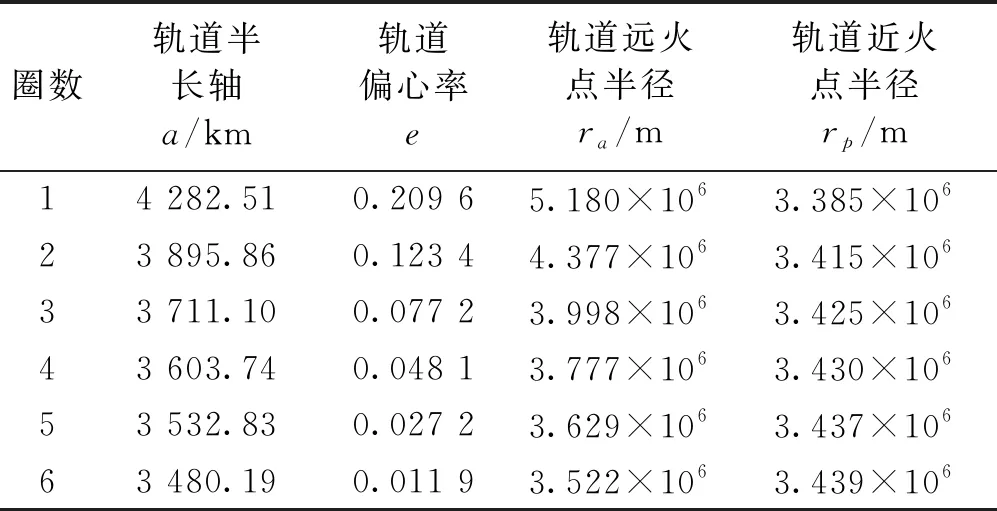
表4 穿刺探测轨道每圈的轨道参数

5 结论

1)所构建的轨道-弹道动力学模型以及参数方程是正确有效的，为火星大气电离层穿刺探测飞行提供了模型基础。

2)建立多次改变近地点幅角的轨迹优化设计模型，通过敏感性分析方法确定优化变量和终端状态约束条件，为火星大气电离层穿刺探测飞行提供了可行的理论方法。

3)提出基于Gauss伪谱法的穿刺探测轨迹优化方法，并通过仿真验证飞行器能够完成火星大气层内外6次穿刺探测飞行，并且近地点幅角的改变量满足任务要求，实现了对火星大气的完整探测。