节段预制梁桥短线匹配的几何控制改进方法

贾布裕， 茅思奕， 陈扬文， 余晓琳， 颜全胜

(华南理工大学 土木与交通学院，广东 广州 510640)

目前，节段预制拼装技术在世界各地被广泛应用于桥梁快速施工。推动节段预制拼装施工方法不断发展的原因在于该方法具有统一生产、自动化程度高、施工速度快、工期短、模板利用率高、施工占地小、收缩徐变小、对桥梁施工周围的环境影响小等优点。自20世纪50年代初，Eugène Freyssinet和Jean Muller发明预制拼装施工技术后，世界范围内已经建造了大量的节段预制拼装桥梁[1-2]。值得一提的是，中国这个最大的桥梁建设之国，目前正在大规模采用基于短线匹配的桥梁建设技术。于2001年3月投入使用的上海浏河大桥主桥采用“混凝土节段箱梁拼装”施工工艺，是中国首次采用短线法预制生产宽节段的工程[3]。于2008年6月30日建造完成的中国苏通大桥采用箱梁节段短线法匹配预制和悬臂拼装法施工[4]，其跨径为1 088 m，是中国当时最大，最复杂的特大型桥梁工程。2015年完成的中国泉州跨海大桥引桥成功实现了基于节段预制拼装技术的大宽幅箱梁施工[5]。2019年完成的中国虎门二桥规模巨大[6]，长度达12.89 km，其引桥大部分采用短线匹配法，节段数量达到3 533。除了这些超级工程，还有一些中国著名的桥梁工程，如南京四桥[7], 芜湖长江公路二桥[8]都采用了节段预制拼装技术。在预制悬臂拼装施工中，节段预制方法一般可分为长线法和短线匹配法[9]。长线法具有几何控制较为简单、占地面积较大、成本较高、对于平纵曲线不同的梁难以适应、灵活性较差等特点，而短线法则具有几何控制要求极高、占地面积较小、灵活性较强、施工快、质量易控制、经济性更高等特点[10]，目前已成为节段预制拼装桥梁的主流施工方式。几何控制被视为是短线匹配法中的最关键的一个环节。目前关于短线匹配法中的几何控制方法主要有2大类：1)理论分析法：通过尽可能精确的误差理论分析来提高几何控制精度，2)先进技术控制法：通过采用先进施工及测量技术来提高几何控制精度。在理论分析方法中，按误差在下一阶段的调整情况，可分为直接调整法[11]和间接调整法[12]；而按误差调整所处坐标系的不同又可分为，局部坐标系调整法[11，13]和整体坐标系调整法[14]。在先进技术控制法中，目前主要采用激光扫描加BIM模型的技术方法[15-19]，通过将BIM技术和激光扫描技术引入到基于短线匹配法的节段预制拼装桥梁施工，可有效提高几何控制精度[20-21]。不可否认，通过先进的技术可以降低施工中的误差，但在施工中总会存在各种不确定因素，不可避免地产生无法消除的误差。对这些误差的精确分析是实现几何控制的前提条件。本文将围绕绕短线匹配法中几何控制的误差分析，准确认识几何控制中误差的来源本质，并通过对传统几何控制方法的改进，提出了一种高精度的几何控制方法，可望为以后的基于短线匹配法的节段预制拼装桥梁的发展和推广提供技术支持和理论基础。

1 短线匹配法中的几何控制

1.1 短线匹配法

短线匹配法是将桥梁主梁提前划分为若干短段，并逐一进行预制的一种施工方法。其具体流程如下。

1)在初始阶段(预制0#节段)，活动端模作为0#节段后端截面，并以固定端模作为0#节段前端截面，而后开始0#节段的混凝土浇筑。

2)当0#节段完成养护后，向前移动作为匹配梁(此时0#节段作为1#节段后端的活动端模)；而固定端模仍作为1#节段前端截面，而后开始1#节段的混凝土浇筑。

3)1#节段完成养护后，运走0#节段，并将1#节段前移作为匹配节段(此时1#节段充当2#节段的活动端模)，继续利用固定端模作为2#节段的前端截面，开始2#节段的混凝土浇筑。

4)重复这个过程, 将第N节段前移作为匹配梁，辅助第N+1节段浇注, 直到所有节段预制完毕。

1.2 预制误差调整

实在节段预制过程中，不可避免地施工误差会导致实际线形偏离理论线形。预制过程中的误差主要有尺寸误差(如长宽)及偏角误差，其中偏角误差是影响线形的主要因素。在短线匹配法中，如前文所述，在预制阶段即使是毫米级单位的误差也可能在最后放大到米级单位的误差，因此每一阶段的误差必须得到及时的分析和调整。图1给出了偏角误差示意图，这里匹配梁假设为(n-1)#，浇筑梁为n#，由于施工误差，测量发现(n-1)#实测和理论的偏角误差为θ，但需要注意的是：实际上这个偏角误差θ并非由(n-1)#引起，而是由n#引起，因为在短线匹配预制中，匹配块(n-1)#，在这个相对局部坐标中，是默认几何准确的，不存在偏差的问题，而偏差只可能存在于待浇筑的预制块n#中，所以，这里测量得到的偏角误差θ应被视为n#的偏角误差。

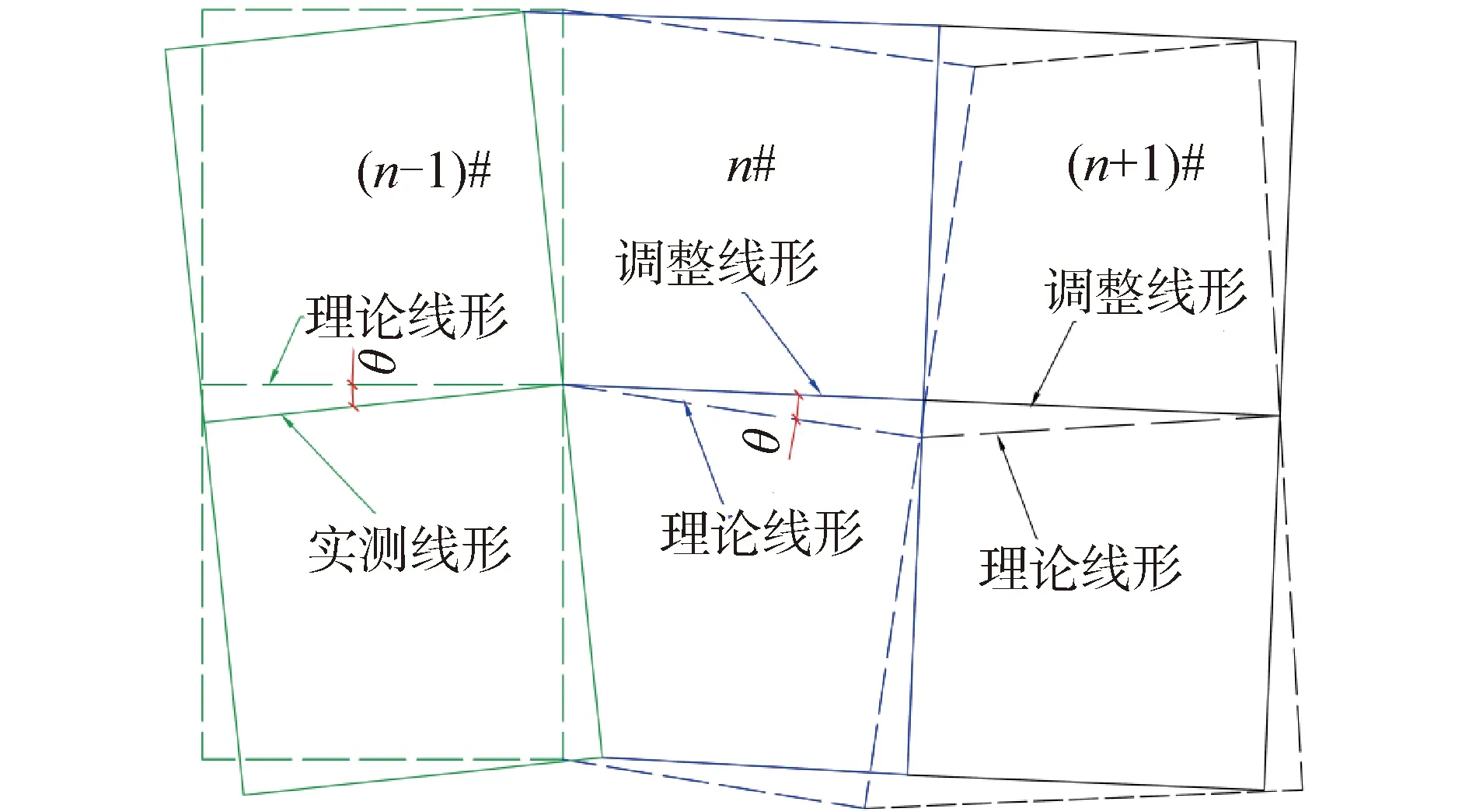
图1 偏角误差分析

在短线匹配法中，需要通过预埋测试点来实现节段梁的误差调整和定位放样(图2)，预埋测试点共设有6个：2个水平测试点(FH、BH)及4个高程测试点 (FR、BR、FL、BL)。水平测试点为倒U型钢预埋件，高程测试点为十字头镀锌螺栓。除了这6个测试点，还有一定数量的梁端定位控制点(图2的I、J、K、V)，用于校核和坐标定位。预制现场的坐标测量主要通过前后2个测量塔来完成，前后2个测量塔位于预制梁的中线上并且垂直于固定端模。

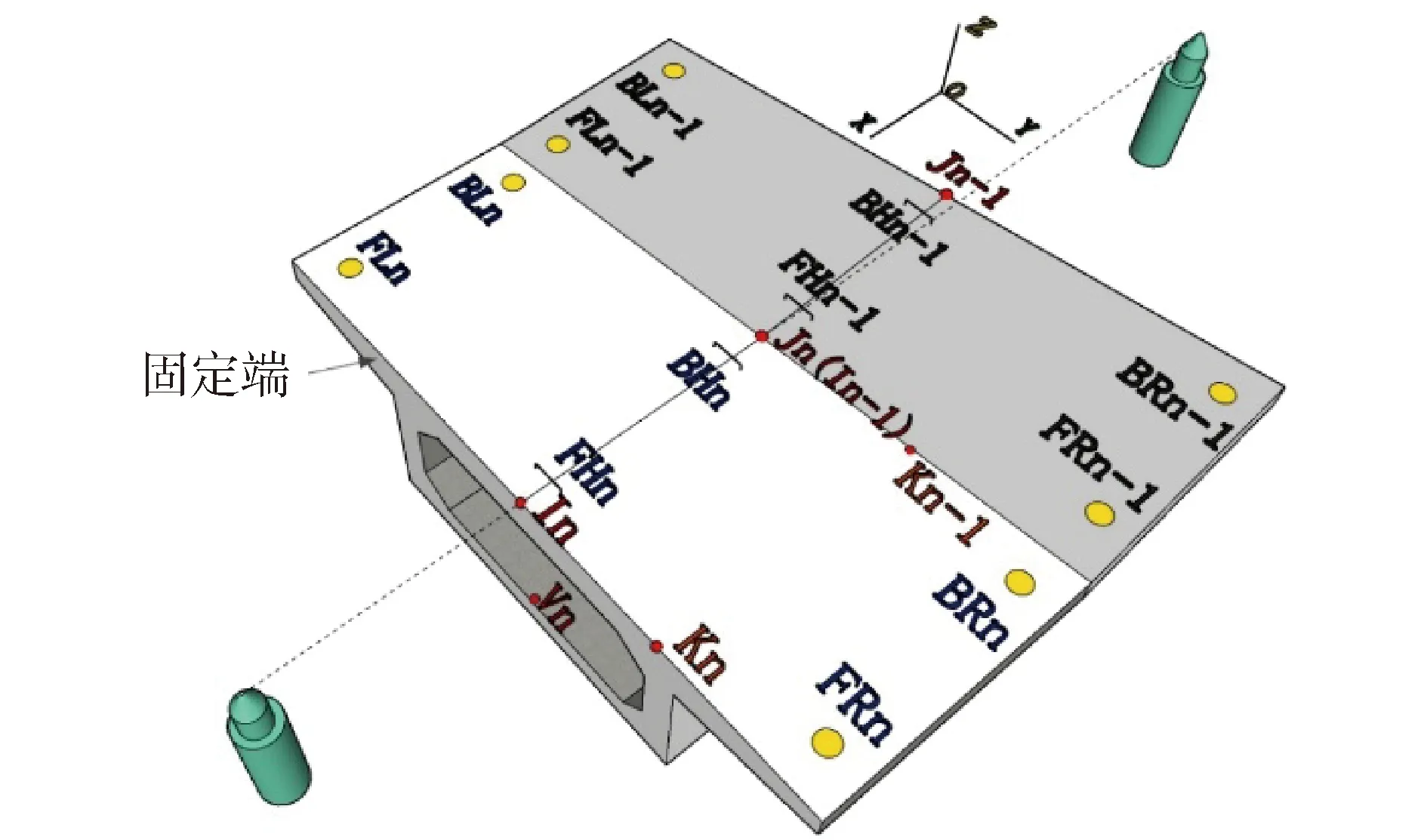
图2 测量系统

1.3 传统几何控制方法以及局限性

目前已有的几何控制技术有力地保证了基于短线匹配法的节段预制拼装技术在桥梁中被广泛应用(尤其在中国)，但随着施工环境的改变以及施工要求的提高，原先的一些适用于简单形式桥梁的几何控制方法的精度不再满足要求。首先，目前由于节段预制梁成为大规模桥梁工程主要采用结构形式，节段梁的数量规模越来越庞大，导致对施工进度提高的要求越来越高，相应地，对几何精度的要求也越来越严格，因为任何其中一片梁的施工误差都可能对施工进度造成破坏性的影响。其次，短线匹配法目前逐渐被推广到空间曲线梁(如带有横坡的曲线梁)，空间角度耦合明显，几何控制变得不再容易。目前已有传统几何控制方法存在的明显局限性归纳如下：

1)局部和整体之间的坐标转换是短线匹配法的核心环节，传统方法往往采用基于多点数据的非线性最小二乘法或者规划求解法进行坐标转换。如果在施工质量得到保证，使得(n-1)#块多个控制点所在的顶面空间位置刚好接近于平面，那么这种类型方法是可以得到良好解的。我们知道任选3个点可以确定一个平面，但在实际施工的时候很难保证剩下多余的点也在同一个平面上，这在体系转换计算的时候会造成难解，即使采用最小二乘法或者规划法求解也很难保证精度，容易造成这样一个结果：个别点预测结果很好，但其他点可能有很大的偏差。

2)传统方法没有考虑控制点连线和预制段轴线之间存在夹角问题，缺乏对不同位置偏差角的区分识别技术。主要是指已有传统方法将BH-FH连线水平方向等同于J-I轴线水平方向：将BH-FH连线的测量(耦合)水平角来等同于梁块轴线(J-I)测量(耦合)水平角，同时将BL-FL连线(右侧BR-FR连线)竖向方向等同于J-I轴线竖向方向。

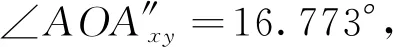
在短线匹配法中，已有传统方法将BH-FH连线水平方向等同于梁块J-I轴线水平方向：将BH-FH连线的测量水平偏差角来等同于块J-I轴线的测量水平偏差角，同时将BL-FL连线(或右侧BR-FR连线)竖向方向等同于J-I轴线竖向方向：将左侧BL-FL连线或者右侧BR-FR连线的测量竖向偏差角来等同于J-I轴线的测量竖向偏差角。但是这些控制点并不是按照指定位置精确埋设的，而是按照大概位置埋设，这样会导致控制水平方向的BH-FH连线和J-I轴线在水平方向存在夹角，同时控制竖向方向的左侧BL-FL连线以及右侧BR-FR连线和J-I轴线在竖向方向也存在夹角。而图3中的OA相当于(n-1)#块的BH-FH连线(或是左侧BL-FL连线、右侧BR-FR连线)，OB相当于(n-1)#块的J-I轴线。这意味着，不应该用BH-FH连线的测量水平耦合偏差角来等同于J-I轴线的测量水平耦合偏差角，同样不能将左侧BL-FL连线或者右侧BR-FR连线的测量竖向偏差角来等同于J-I轴线的测量竖向偏差角。如果施工单位在每块施工时都能按照和轴线平行要求埋设控制点，那么这种近似考虑造成的误差可能不是很大，但遇到控制点连线和轴线存在较大夹角时，这种近似考虑会造成较大的误差，在短线匹配这种以毫米精度作为要求的施工中，这种误差很可能会对后续的线形控制造成很大的麻烦。

图3 不同斜率直线转动后水平、竖向耦合角示意

2 几何控制改进方法

针对上述局限问题，本研究提出一套新型的几何控制方法，具体如下。

2.1 基于三控制点的改进局部与整体坐标相互转换系统

2.1.1 坐标相互转换系统ISGL

本研究坐标相互转换系统(interconversion system between global coordinate and local coordinate，ISGL)基于三点七参数法[22]，其中三点为两坐标系统下公共点数，即图3所示J、I、K三点或V、I、K三点，而七参数则为一个尺度参数、3个平移参数、3个旋转参数。首先得到坐标转换的基本数学模型(这里假设从局部坐标系In-xyz转换到整体坐标系O-XYZ)：

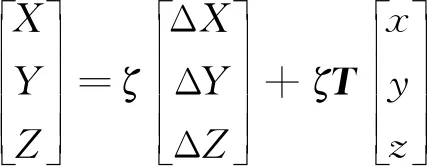
(1)

式中：ζ为尺度缩放因子，又称为尺度参数，[ΔXΔYΔZ]T为平移参数；T为坐标转换旋转矩阵T=TZTXTY，TZ为局部坐标绕整体坐标Z轴旋转θZ角得到的旋转矩阵；TX为局部坐标绕整体坐标X轴旋转θX角得到的旋转矩阵；TY为局部坐标绕整体坐标Y轴旋转θY角得到的旋转矩阵。T可写为：

(2)

一般，ζ、 ΔX、 ΔY、 ΔZ、θX、θY、θZ被称为七参数。接下来简述如何求解这七参数。首先，可容易先确定尺度参数ζ：刚体对应边长比的平均值。问题的关键在于如何求解转角3个参数θX、θY、θZ。设T为正交矩阵，可知其中只有3个元素是独立的。

设有这3个独立元素组成的反对称矩阵R:

(3)

则T可转换为由R构成的罗德里格矩阵：

(4)

同时可知：

TT=T-1=(I+R)-1(I-R)

(5)

设3个公共定位点J、I、K，其在整体坐标系下的坐标分别为(XJ,YJ,ZJ)、(XI,YI,ZI)、(XK,YK,ZK)，其在局部坐标系下的坐标分别为(xJ,yJ,zJ)、(xI,yI,zI)、(xK,yK,zK)。将J、I、K(或V、I、K)三点坐标代入式(1)中建立9组方程，并结合式(5)，经整理得到3个独立方程：

(6)

其中：Δ1=ζ(xI-xJ)-(XI-XJ); Δ2=ζ(yI-yJ)-(YI-YJ); Δ3=ζ(zK-zJ)-(ZK-ZJ);a2=ζ(xI-xJ)+(XI-XJ);b2=ζ(yI-yJ)+(YI-YJ);c2=ζ(zI-zJ)+(ZI-ZJ);a3=ζ(xK-xJ)+(XK-XJ);b3=ζ(yK-yJ)+(YK-YJ)。求解方程组(6)得：

(7)

求得r1、r2、r3后，则可以根据式(8)得到转角参数θX、θY、θZ：

(8)

接着根据式(1)可得到平移3个参数ΔX、 ΔY、 ΔZ：

(9)

七参数都已确定，坐标相互转换系统ISGL便可建立。

2.1.2 基于交叉验证CV思想的改进ISGL

交叉验证(cross validation，CV)是一种经常被用于评判模拟模型性能优劣的方法，其基本思想是：首先将数据分为训练组和验证组，接着利用训练组建立模拟模型，再利用验证组测试模拟模型的性能。由上文可知，坐标相互转换系统的精度取决于定位控制点，而由于测量误差的存在，定位控制点存在不可避免的偏差，因而坐标相互转换系统也并不能时时保证完全准确。为提高坐标相互转换的精度，本文启发于CV思想，提出以下改进方法：

1) 设置Vn、In、Kn、Jn、Kn-1为定位控制点，以3点为一组，共有10组定位控制点数据：(Vn,In,Kn)、(Vn,In,Jn)、(Vn,In,Kn-1)、(Vn,Kn,Jn)、(Vn,Kn,Kn-1)、(Vn,Jn,Kn-1)、(In,Kn,Jn)、(In,Kn,Kn-1)、(In,Jn,Kn-1)、(Jn,Kn,Kn-1)。基于这10组数据，建立10套坐标转换系统-ISGL。

2)选取其中一套坐标转换系统ISGL，这里假设取基于(Vn,In,Kn)得到的ISGL_a，利用该ISGL_a将Jn,Kn-1的局部坐标转换为整体坐标，并与理论整体坐标进行比较，得到其各坐标值的偏差相对值，同时将各坐标偏差相对值求和得到总偏差值。以此类推，计算剩下9组的总偏差相对值。利用这10套坐标转换系统ISGL得到10组总偏差相对值后，取平均得到总偏差平均相对值。

3)设定一偏差容许界限值δ(这里取0.01)，如果总偏差平均相对值超过这个限值，说明测量质量或者方式有问题，需要重新测量一次，而如果总偏差平均相对值没有超过这个限值，则取10组里面总偏差相对值最小的ISGL作为最终的坐标转换系统。

4)利用最终ISGL，将(n-1)#的6个测点的局部坐标BLLT,n-1…转换为整体坐标数据BLGT,n-1…。

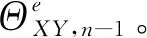
(10)

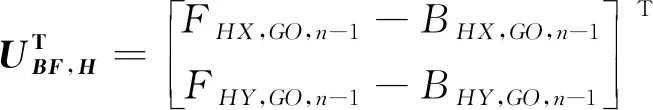
(11)

(12)

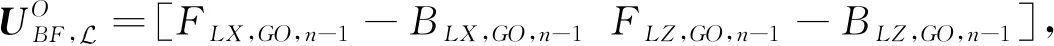
2.2 偏差角度区分方法

如前文所述，由于空间斜率不同，不应该用BH-FH连线的水平耦合偏差角来等同于梁块轴线J-I的水平耦合偏差角，同样不能将左侧BL-FL连线或者右侧BR-FR连线的竖向耦合偏差角来等同于梁块轴线J-I的竖向耦合偏差角。本文采用了迭代收敛的策略，提出了一套能区分匹配段控制点连线(水平及竖向)和梁块两端轴线不同的耦合偏角的技术算法。所提出的方法可分为3个主要步骤：1)根据BH-FH的测量水平耦合偏差角和左侧BL-FL连线的测量竖向耦合偏差角，计算轴线J-I水平和竖向的耦合偏差角以及解耦偏差角的第一组解-这里称为解1。2)基于BH-FH的测量水平耦合偏差角和右侧BR-FR连线的测量竖向耦合偏差角计算轴线J-I水平和竖向的耦合偏差角以及解耦偏差角的第2组解-这里称为解2。3)对解1和解2进行平均，得到最终结果。1)子步骤详细如下：

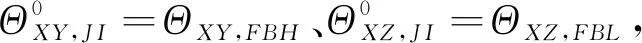
② 利用解耦系统，得到解耦的轴线J-I水平偏差角ΦXY,JI(中间值)和解耦的轴线J-I竖向偏差角ΦXZ,JI(中间值)；

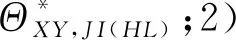
④ 进行收敛判定：

(13)

⑤ 得到收敛时的轴线J-I的水平耦合偏差角ΘXY,JI和水平解耦偏差角ΦXY,JI，以及轴线J-I的竖向耦合偏差角ΘXZ,JI和竖向解耦偏差角ΦXZ,JI。对应的流程见图4。

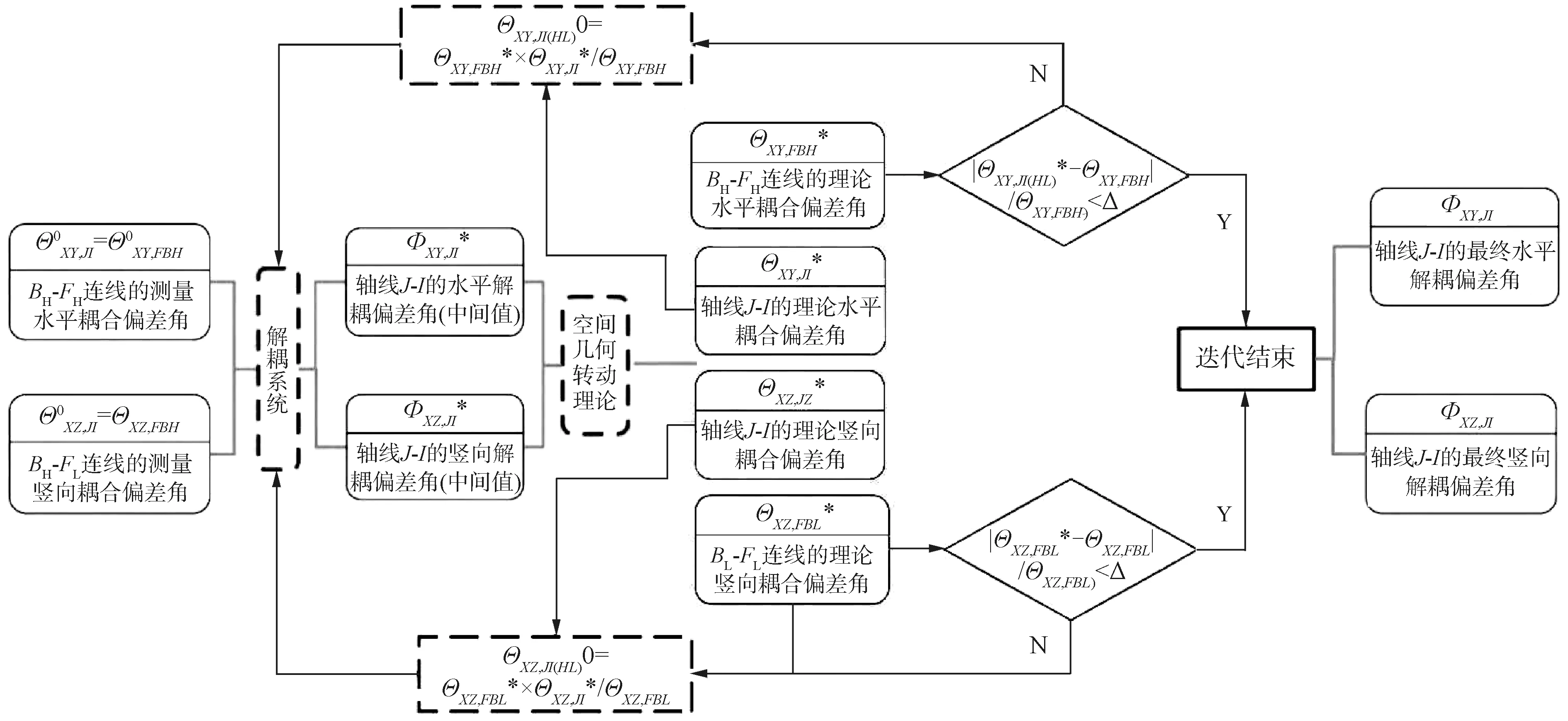
图4 偏差角区分流程

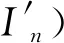
表1 局部坐标下(n-1)#上测点的测试数据和理论数据

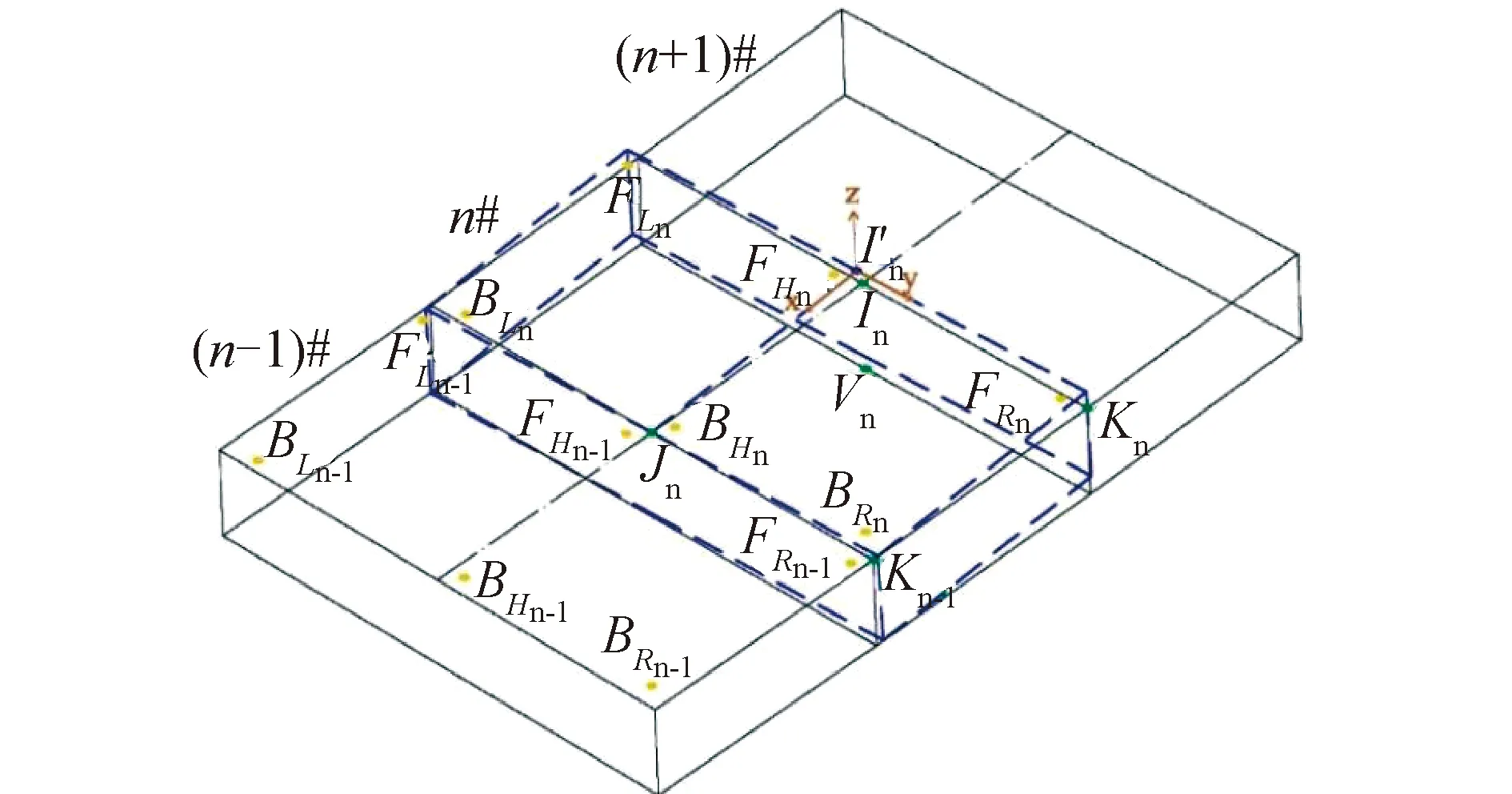
图5 CAD 模拟节段梁

首先，采用传统方法1(包含前文所提两个局限性)得到的轴线J-I水平和竖向偏差角(解耦)为：ΦXY=1.255 4°，ΦXZ=1.732 3°；而采用传统方法2(包含前文所提第2个局限性)得到的轴线J-I水平和竖向偏差角(解耦)为：ΦXY=1.301°，ΦXZ=1.869 6°；采用所提方法求解得到的轴线J-I的水平和竖向偏差角(解耦)为：ΦXY=1.392 6°，ΦXZ=1.798 5°。从这些结果中，可知传统方法1的误差分析精度最低，而改进了坐标转换系统之后的传统方法2的误差分析精度有所提高，但仍和真实模拟结果有较大差距，而本文的所提改进方法的结果和真实模拟结果几乎一致，验证了本研究所提方法的有效性。

3 所提方法在实桥项目中的应用

3.1 项目概况

以某在建城市桥梁为例，其上部结构为预应力混凝土连续箱梁，跨径组合为4×(5×60) m，全长1 200 m，桥宽33 m，分左右幅布置，单幅宽16.25 m。主梁采用单箱单室直腹板断面，顶底板平行，横坡通过绕桥面设计高程点整体旋转形成。主梁划分为712榀节段，采用短线法在工厂逐块匹配预制节段梁。主梁节段划分如图6所示。

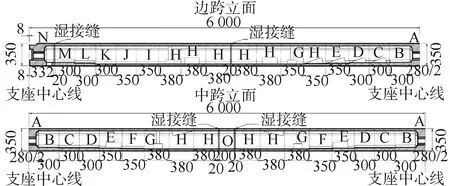
图6 节段梁划分布置 (单位：厘米)

3.2 几何控制结果

出于比较和验证的目的，除了所提方法被用于该实际桥梁的几何控制，同时也采用了传统方法，这里传统方法是指未得到改进(即包含有前文所提的2个局限性，其中坐标转换方法为采用基于“6点”的非线性最小二乘法)的方法。由于短线匹配法是一个连贯的过程，每个悬臂只能采用一种几何控制方法；但同时考虑到该桥所有梁段均在同一场地施工且采用相同的施工设备、施工工艺、施工队伍、测量设备，因此经过综合考虑，采用传统方法对左幅第27#悬臂进行几何控制，而采用本研究所提方法对该桥左幅的第28#悬臂进行几何控制。将每一节段的匹配梁上6个控制点的实测数据和理论值即匹配指令进行分析比较，得到各个控制点坐标的偏差值。这里选取梁块前段3个点(FL、FR、FH)的数据，其中FL和FR取竖向坐标(Z)偏差值，FH取水平坐标(X、Y)偏差值。图7给出了基于传统方法的27#悬臂的匹配节段的测点坐标偏差结果，图8给出了基于所提方法的28#悬臂的匹配节段的测点坐标偏差结果。首先，从两者的比较结果可知，采用传统方法的几何控制效果较差，最大的偏差达到9.56 mm，而采用本文所提方法得到的几何控制效果有明显的改进，其最大的误差仅为3.8 mm；其次，在传统方法中(图7)，竖向误差明显比水平方向误差大，而在所提方法得到的结果中，3个方向的坐标偏差基本相近，相差并不大。传统方法采用基于“6点”非线性最小二乘法的坐标转换系统，如前文所述，在实际施工的时候很难保证数量超过3个的点全部在同一个平面上，这在体系转换计算的时候会造成难解，尤其会造成空间差异较大方向的坐标转换出现较大偏差(如竖向)；再有，从图7中可知，在传统方法中，在预制LE4#节段和LW5#时出现了较大的几何偏差，而我们实际现场中发现这2个梁块出现了控制点连线和轴线存在较大夹角的情况，这有力证明了偏差角区分识别的必要性。为了直观显示整个悬臂施工阶段的整体控制效果，图9给出了2种方法关于整个悬臂所有节段的坐标偏差(绝对值)的平均值结果，从中可知基于所提方法得到的4个点坐标的整体偏差平均值均小于传统方法的结果，再次说明了所提方法的优越性。

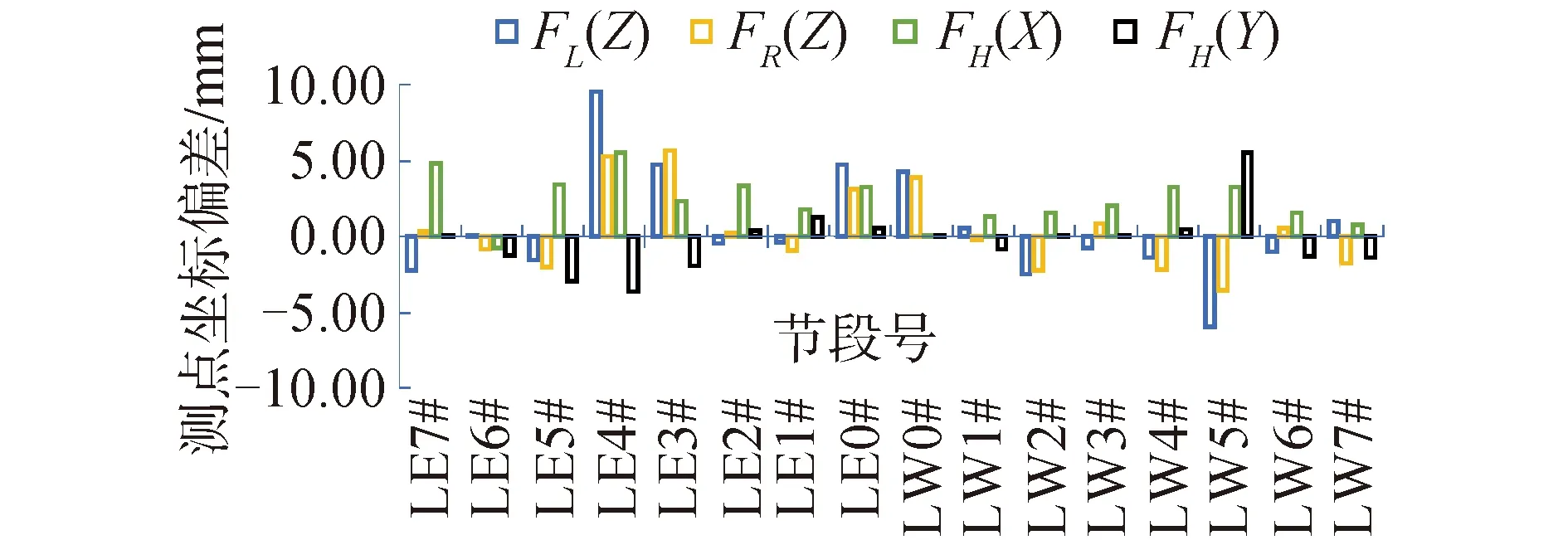
图7 27#悬臂的匹配节段的测点坐标偏差(传统方法)

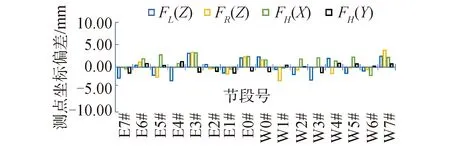
图8 28#悬臂的匹配节段的测点坐标偏差(本文方法)

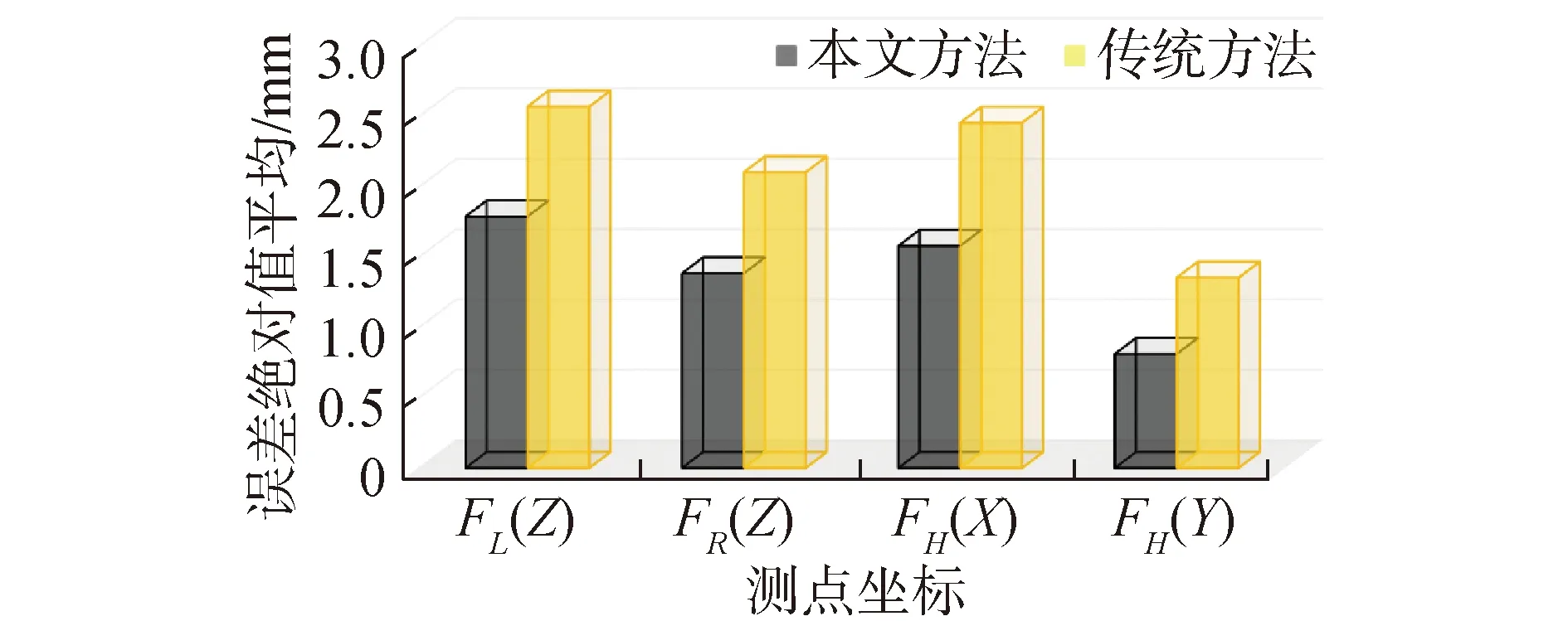
图9 所有阶段的测点坐标偏差统计值比较

4 结论

1)采用传统方法的几何控制效果较差，最大的偏差达到9.56 mm，而采用本文所提方法的最大误差仅为3.8 mm；

2)传统方法由于采用基于“6点”非线性最小二乘法的坐标转换系统，容易造成空间差异较大方向的坐标转换出现较大偏差；而本文所提方法个方向的坐标偏差基本相近，相差并不大；

3)本文方法在整体偏差效果方面明显优于传统方法(所提方法的整体偏差平均值均小于传统方法的结果)。这些充分说明了本文所提方法具有工程应用的有效性和优越性。

需要指出的是，本文所提方法局限于预制阶段，并未涉及到拼装阶段的几何控制；而拼装阶段的几何控制对整个成桥线形同样具有重要影响，因此将来将围绕拼装阶段的高精度几何控制展开进一步的研究工作。