基于扩展卡尔曼滤波的无速度传感器无刷双馈感应电机直接转矩控制

郑诗程，周甜军，郎佳红

（1.安徽工业大学电气与信息工程学院，马鞍山 243000；2.安徽省电力电子与运动控制重点实验室（安徽工业大学），马鞍山 243000）

无刷双馈电机BDFM（brushless doubly-fed machine）是一种新型电机[1]，由于其取消了电刷和滑环以及大大降低了变频器容量，在交流调速系统和变速恒频发电领域具有很好的研究前景。按转子结构的不同，BDFM 可分为无刷双馈磁阻电机BDFRM（brushless doubly-fed reluctance machine）和无刷双馈感应电机BDFIM（brushless doubly-fed induction machine）两种[1]，在传统的BDFIM 转矩控制中往往需要实时检测定子绕组的各相电压、电流以及转子速度，进而计算磁链和电磁转矩。但是转速信息一般需要通过机械式传感器测得，其测量精度容易受到环境影响，而且对安装同轴度要求较高，同时系统的硬件成本高，电机的体积质量大。为了克服传统机械式传感器的缺陷，可以将适用于异步电动机的无速度传感器技术应用到BDFIM 的转矩控制当中。

目前，针对BDFIM 的无速度传感器控制的研究相对较少，文献[2-5]将无速度传感器技术应用于BDFRM 调速、风力发电领域。比较成熟的无速度传感器控制技术主要包括滑模观测器、龙贝格观测器、模型参考自适应系统、扩展卡尔曼滤波器EKF（extended Kalman filter）等[6-9]。EKF 适用于含有噪声的随机系统，并且EKF 中转速是作为状态变量进行估计的，对噪声具有很强的免疫力。

本文以三相BDFIM 为研究对象，通过对转子速度坐标下的数学模型分析，建立系统的状态方程和观测方程，实现基于EKF 算法的转子速度和功率、控制绕组磁链的估计，提出一种基于EKF 无速度传感器的DTC 策略，根据磁链的估计值计算出转矩大小，并对控制绕组的磁链进行定向和逆变器开关状态的判定。最后通过仿真结果验证所提控制策略的有效性。

1 基于EKF 的速度和磁链估计

1.1 三相BDFIM 数学模型

忽略磁饱和效应，BDFIM 在转子速度坐标系下的非线性数学模型[10-11]分别为电压方程、磁链方程、转矩方程和运动方程，表示为

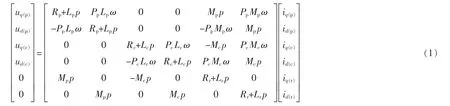
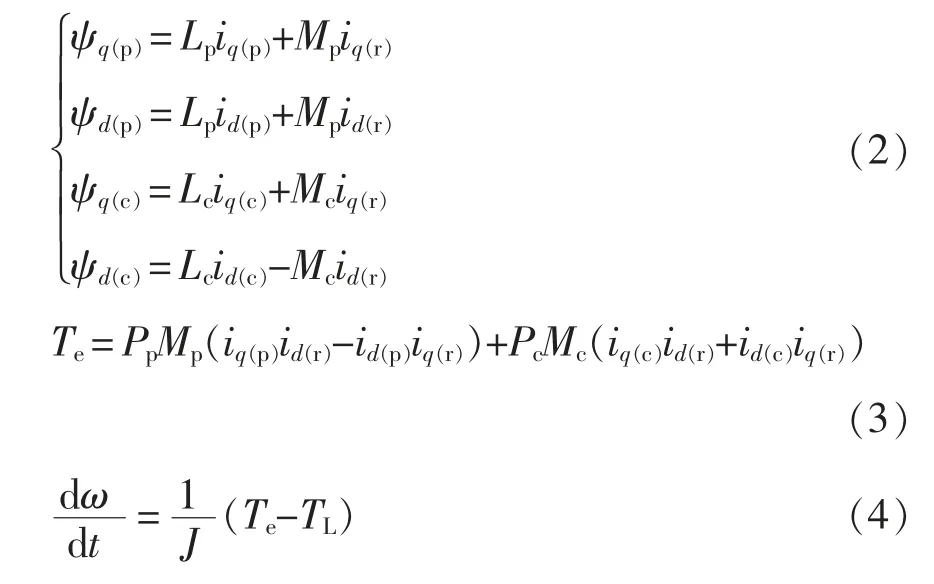
式中：Pp为功率绕组极对数；Lp为功率绕组自感；Mp为功率绕组互感；Rp为功率绕组电阻；ψq（p）为功率绕组磁链q 轴分量；ψd（p）为功率绕组磁链d 轴分量；Pc为控制绕组极对数；Lc为控制绕组自感；Mc为控制绕组互感；Rc为控制绕 组电阻；ψq（c）为控制绕组磁链q 轴分量；ψd（c）为控制绕组磁链d 轴分量；Lr为转子绕组自感；Rr为转子绕组电阻；ω 为转子的机械角速度；p 为微分算子；J 为转动惯量；Te为电磁转矩；TL为负载转矩；Kd为阻尼系数；下标p 表示功率绕组；下标c 表示控制绕组；下标r 表示转子绕组。

1.2 状态方程和观测方程的建立

为了实现在辨识转速的同时观测磁链，取状态变量为

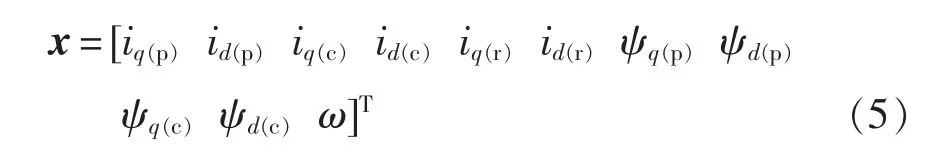
输入变量为

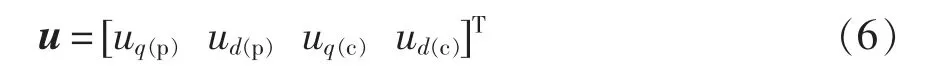
输出变量为

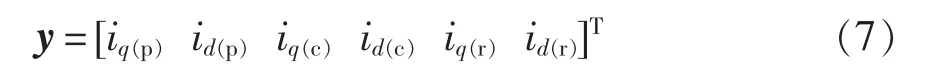
在采样周期很小或负载转动惯量很大时转速的变化可以忽略不计，假设dω/dt=0。在扩展卡尔曼滤波观测器中，可将这种忽略引起的误差作为系统噪声处理，在递推计算中给予必要的校正[9]。并结合式（1）～式（2）可推导出

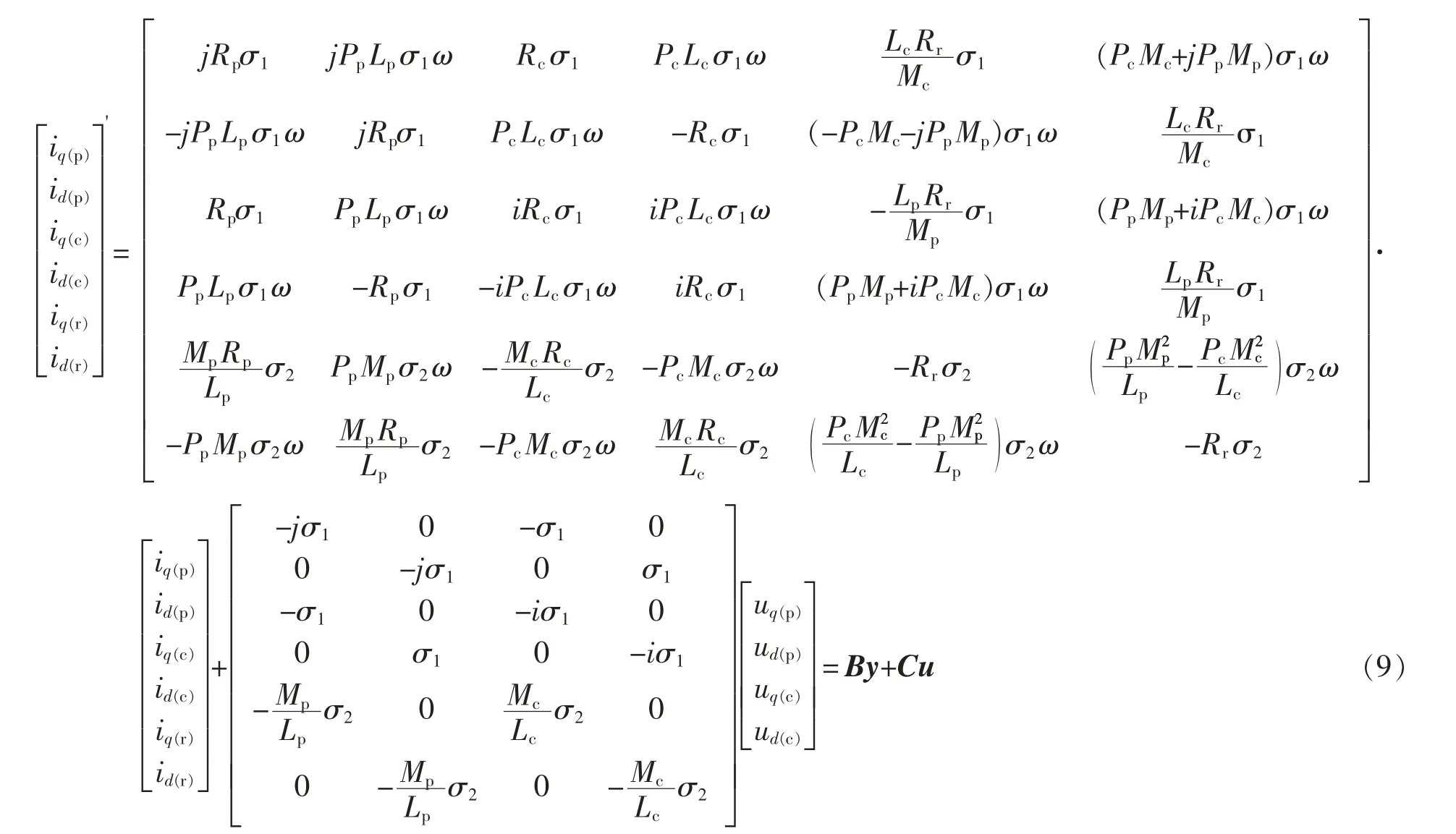
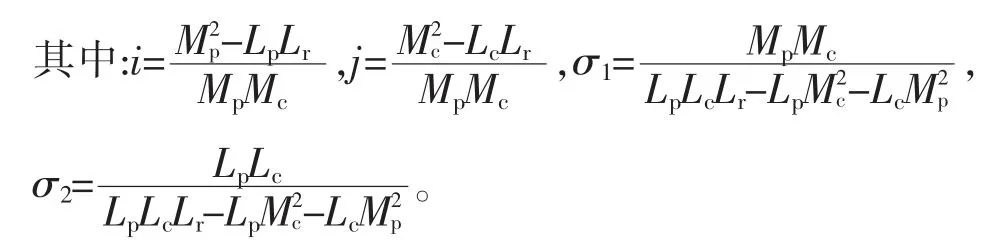
由式（8）～式（9）可以得到三相BDFIM 状态方程和观测方程为

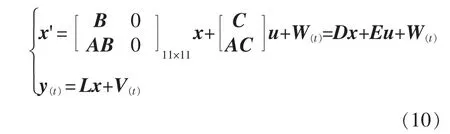
其中，矩阵L 为

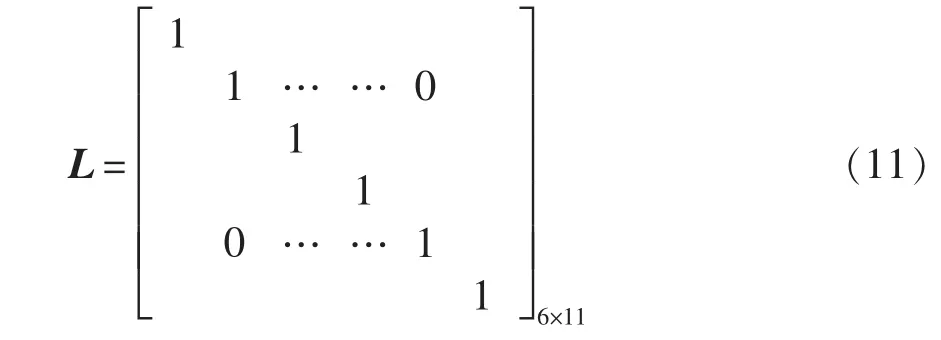
式中，W（t）、V（t）分别为系统噪声和观测噪声。

1.3 EKF 的实现

1.3.1 系统的离散化

以T 为采样周期，将式（10）离散化可以得到系统的非线性离散化方程[12-13]为

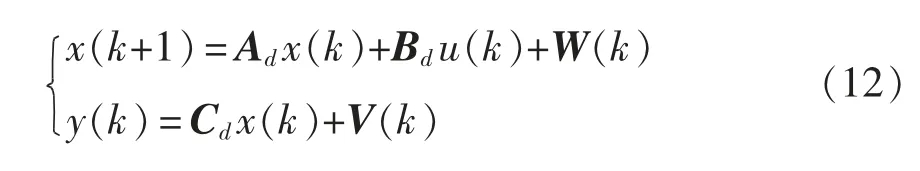
1.3.2 雅克比矩阵的计算

系统离散化后的雅克比矩阵为

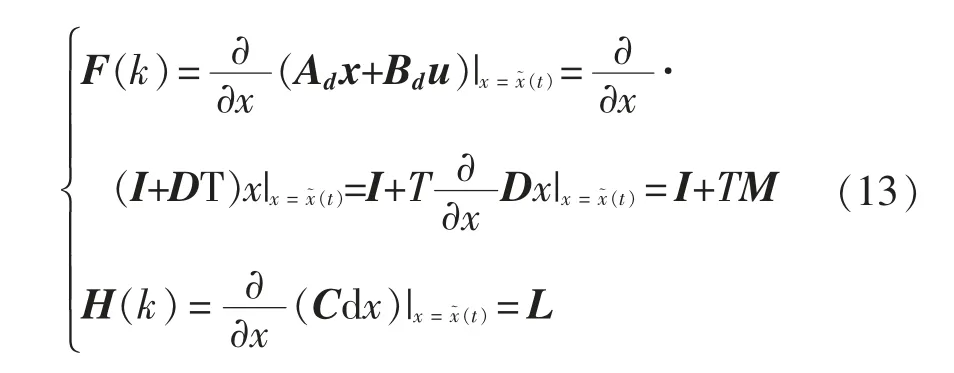
1.3.3 泰勒级数展开

对式（12）在状态估计值附近进行泰勒展开，略去阶数高于1 的项，可以得到系统的线性离散化方程为

式中，W（k）和V（k）满足

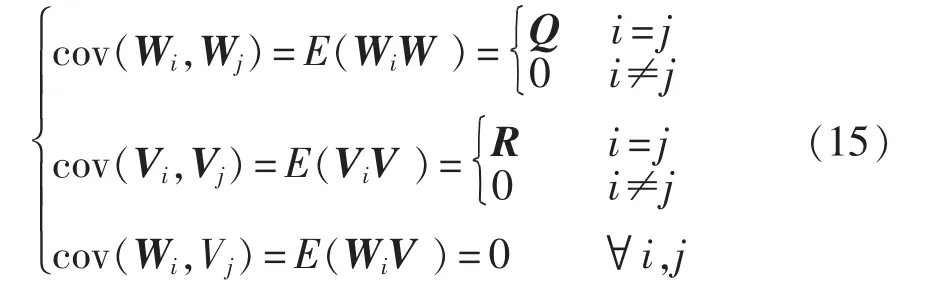
式中，Q、R 分别为W（k）和V（k）的协方差矩阵。

1.3.4 预报阶段

状态预测值为

状态协方差矩阵的预测值为

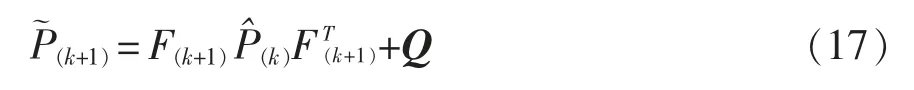
1.3.5 滤波阶段

卡尔曼增益矩阵为

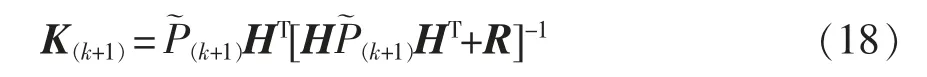
状态估计值为

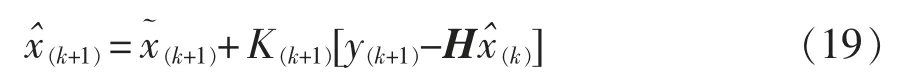
更新状态协方差矩阵的估计值为

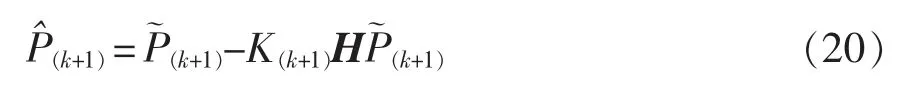
2 基于EKF 的BDFIM 直接转矩控制系统

基于EKF 的BDFIM 直接转矩控制系统的结构如图1 所示，主要包括EKF、转矩观测器、磁链分析和开关状态表。为速度、电磁转矩和控制绕组磁链的给定值，n、Te、ψc为对应的反馈值，ΔT、Δψ 为相应的误差值，Sx和Vx分别为控制绕组磁链所在扇区和6 路开关信号。

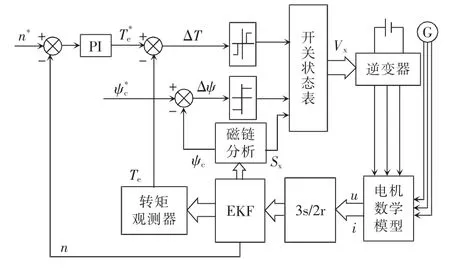
图1 基于EKF 的直接转矩控制系统结构框图Fig.1 Block diagram of EKF-based direct torque control system

2.1 磁链的分析

首先将由EKF 估算出来的ψd（c）和ψq（c）进行dq到αβ 的坐标变换，根据控制绕组磁链在αβ 轴上的分量ψα（c）和ψβ（c）来确定磁链矢量和所在扇区。

控制绕组的磁链大小为

矢量的角度值计算见表1，磁链所在扇区的确定见表2。

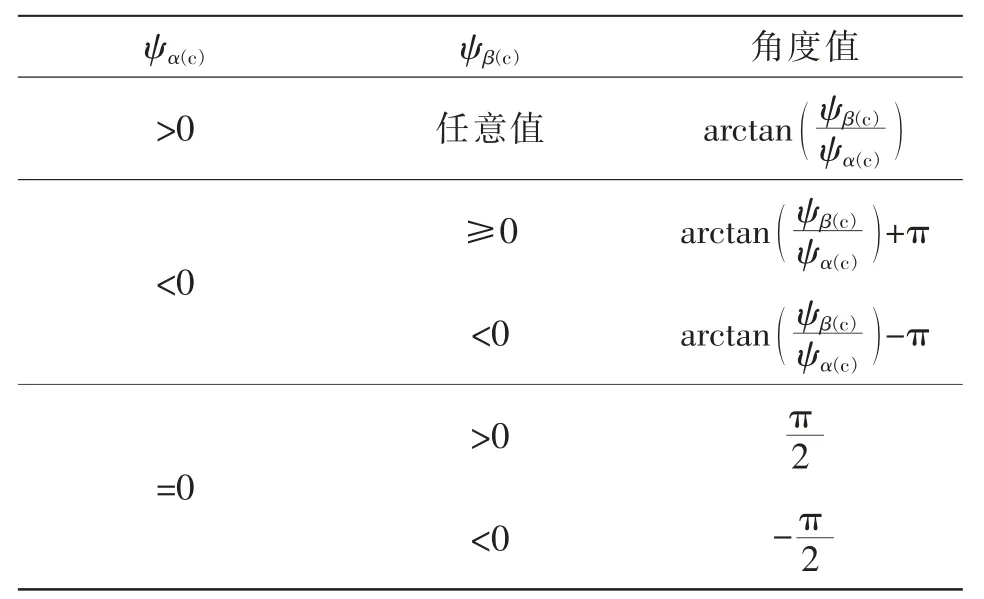
表1 角度值计算Tab.1 Calculation of angle

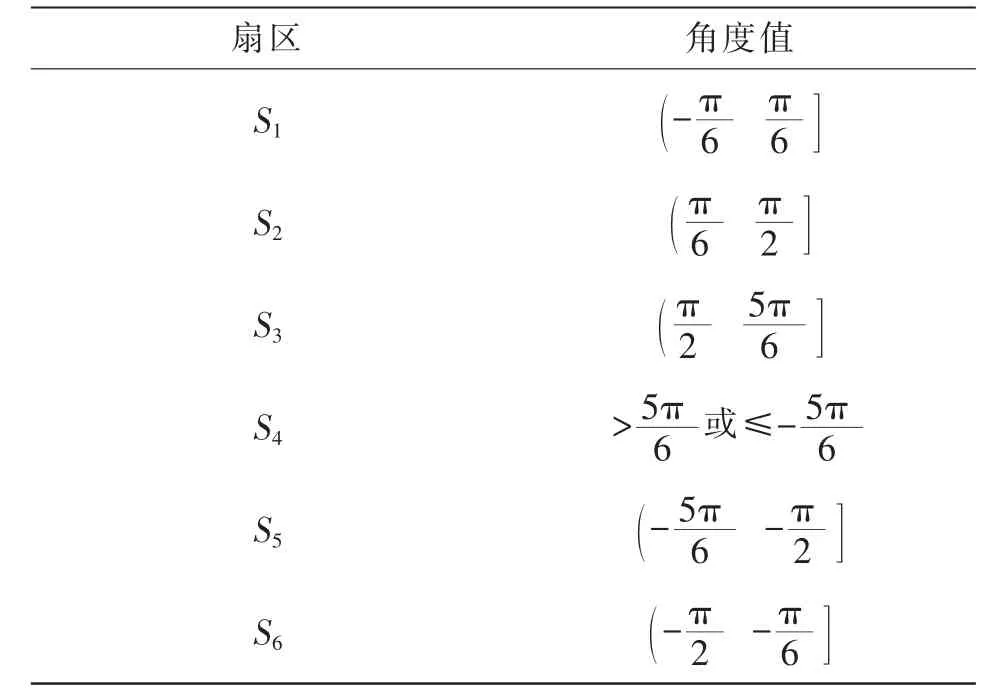
表2 扇区确定Tab.2 Determination of sector

2.2 转矩的观测

在转矩观测器中，根据EKF 估计出来的绕组磁链和电流的观测值来观测转矩。将磁链方程（2）代入到转矩方程（3）中，化简后为

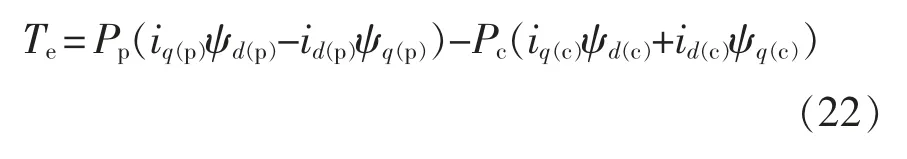
2.3 开关状态表的设计

无刷双馈电机的电磁转矩和磁链之间的关系为

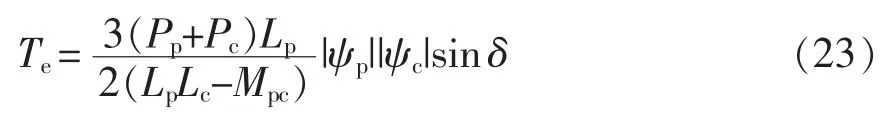
式中，Mpc和δ 分别为功率绕组和控制绕组之间的互感和夹角。

在忽略功率绕组电阻压降时，功率磁链ψp基本不变，所以在DTC 控制中保持控制绕组磁链ψc的幅值不变，通过控制ψc的旋转速度来改变夹角δ，从而控制电磁转矩。

逆变器输出电压的空间矢量[15]和扇区划分如图2 所示。假设一开始控制绕组磁链在第一扇区，若Δψ>0，则需要通过矢量V2或V6来增加磁链，若同时有ΔT>0，则需要通过矢量V2来提高磁链的旋转速度，从而增大转矩，若ΔT＜0，则可选择矢量V6，以减小转矩。

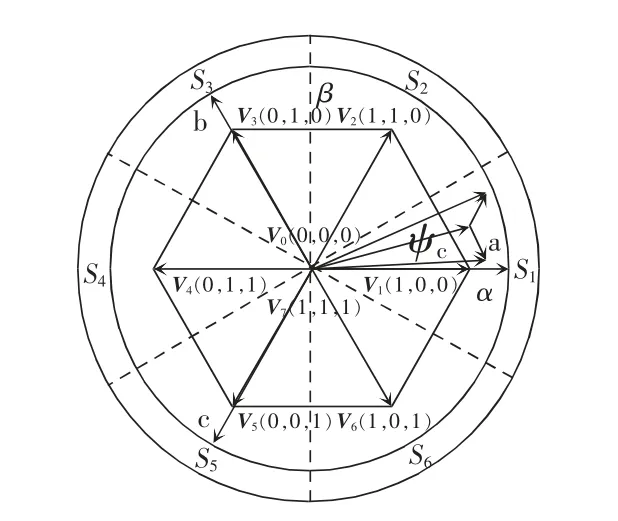
图2 电压空间矢量和扇区划分Fig.2 Division of voltage space vectors and sectors

以此类推，依次建立逆变器的开关状态，表如表3 所示。表3 中，Δψ'=1 表示Δψ≥0，需要增加磁链，Δψ'=0 表示Δψ＜0，需要减小磁链；ΔT'=1 表示ΔT≥ε，需要增加转矩，ΔT'=0 表示|ΔT＜ε|，可选择零矢量（V0或V7），使转矩静止不动，ΔT'=-1 表示ΔT≤-ε，需要减小转矩。

表3 开关状态Tab.3 Switching states

3 仿真分析

为证明基于EKF 的BDFIM 无速度传感器控制策略的有效性，在Matlab/Simulink 仿真软件中搭建BDFIM 和转矩控制仿真模型，并用其中的SFunction 函数模块编写EKF 算法。主要仿真参数如表4 所示。

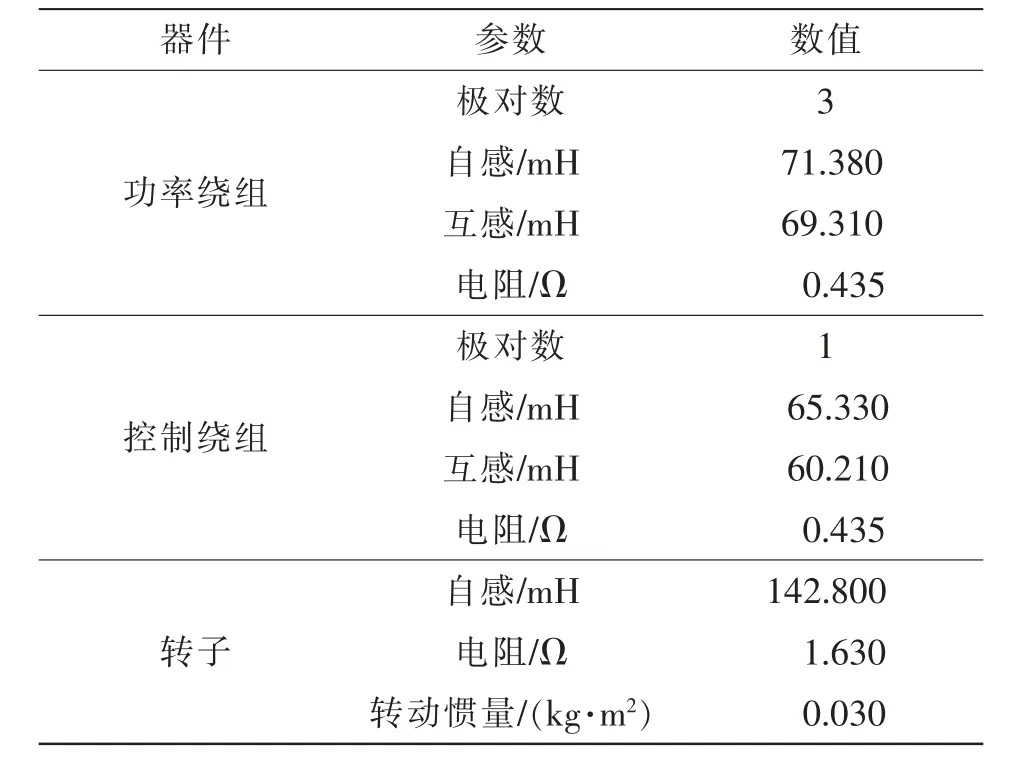
表4 主要仿真参数Tab.4 Main simulation parameters

电机在速度600 r/min、负载10 N·m 下启动，每0.5 s 速度增加100 r/min，直到900 r/min。在t=2.0 s时，负载突减；在t=2.5 s 时，负载突加为10 N·m。仿真结果如图3 所示。

图3（a）中，实际转速在刚开始时振荡比较大，达到1 000 r/min 左右；估计转速也存在一定的波动，大约在0.3 s 后进入稳态，并且在负载增加和负载突减的过程中，估计转速都可以较好地跟踪电机实际转速，与给定转速之间的稳态误差约为2 r/min。图3（b）中控制绕组的估计磁链和实际磁链基本吻合；估计磁链的轨迹为圆形，如图3（c）所示，控制绕组的观测电流刚开始有一定波动，经过0.3 s 后达到稳定；由图3（b）、3（d）可见，电机转速低于750 r/min（仿真时间0～1 s 内）时，控制绕组中的磁链矢量是反向旋转的（与功率绕组磁链相比），当电机转速高于同步转速（仿真时间1～3 s 内）时，控制绕组中的磁链矢量是正向旋转的，且转速随着与同步转速绝对差值的增大而提高。图3（e）中，电磁转矩在刚开始时有较大的波动，为了迅速满足电机转速的给定要求，在负载增加速和突变的瞬态过程中，电磁转矩最大波动范围在10 N·m 以内，稳态误差较小，大约为1 N·m。

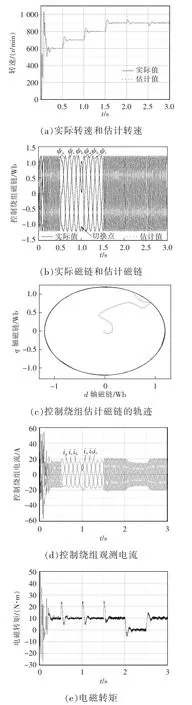
图3 仿真波形Fig.3 Simulation waveforms

4 结语

根据三相BDFIM 在转子速度下的数学模型，建立出系统的状态方程和观测方程，实现基于EKF算法的转子速度的估计和磁链的估计；在直接转矩闭环控制中，EKF 能够在较宽的转子速度范围内实现转速和磁链辨识，在速度给定阶跃变化和负载扰动的动态过程中均表现出较好的动态性能，验证了所提策略的有效性。