Boost 型LED 恒流驱动电路逆系统解耦控制

龚翌凡，陆益民

（广西大学电气工程学院，南宁 530004）

LED 由于寿命长、耗能少、绿色无污染等优点在照明领域得到广泛应用，如住宅照明、交通照明、汽车照明、景观照明等[1-3]。LED 是一种低压直流非线性半导体器件，为精确描述其等效电学参数模型，文献[4]将传统的肖克莱方程和LED 理想物理模型进行结合，对方程进行泰勒展开和分段处理，建立了一种LED 分段数学模型。文献[5]采用5 种数学拟合方法构建LED 的等效电学模型，这些等效电学模型都是非线性模型，并且当LED 导通时，其两端电压的微小变化会使得流过它的电流变化显著，因而需要有相匹配的恒流驱动电路才能使其稳定可靠地发光[6-8]。对于DC-DC LED 驱动电路，通常在建立其小信号模型的基础上，采用峰值电流或平均电流控制方法，以保证输出电流稳定[9-11]。然而小信号建模及线性反馈控制因固有的局限性，难以实现变换器在大信号工作条件下的稳定控制和高动态响应性能。因此，针对DC-DC LED 驱动电路的特点，应采用大信号模型建模，但大信号模型通常为非线性，对系统的分析和综合须借助非线性控制理论。

非线性控制方法能够较好地改善系统的动态特性和稳态特性，如文献[12]基于Boost LED 恒流驱动电路提出了一种滑模变结构控制方法，实现了对LED 的恒流控制，提高了系统的鲁棒性。文献[13]根据无源性控制理论和Lyapunov 稳定性理论，推导出Flyback LED 驱动电路的无源性控制律，实现输出电流的精确恒定控制。应用非线性理论来分析和设计控制系统均是在时域中进行，往往依据稳定性理论设计反馈控制律[14]，这虽能够保证闭环控制系统的稳定性，但难以将控制器的结构和参数与稳态精度、动态响应等具体性能指标建立直接的联系。此外，在采用双闭环控制结构的DC-DC LED 驱动电路反馈回路中，电感电流和输出电压之间存在一定的强耦合关系，因此DC-DC LED 驱动电路的非线性强耦合问题应该得到解决。

逆系统方法是一种线性化解耦控制方法，其基本思想是根据被控对象的数学模型生成一种可用反馈方法实现的α 阶积分逆系统，将被控对象补偿为伪线性系统，进而运用线性系统理论完成伪线性系统的综合[15]。文献[16]针对DC-DC 变换器提出了一种电压电流双闭环的逆系统解耦控制方法。文献[17]基于逆系统方法推导出Buck 变换器的伪线性模型，然后采用变结构控制理论为伪线性系统设计控制律，从而提高系统的抗干扰能力，简化控制器的设计过程，虽然其物理概念清晰直观，数学分析简单，但在DC-DC LED 驱动电路中无法直接应用，主要原因是应用逆系统方法首先需要基于数学模型计算被控对象的逆系统补偿矩阵[18]，DC-DC LED 驱动电路的大信号模型是非线性强耦合系统，难以求得逆系统的解析解。文献[19]针对电流型双有源桥式双向DC-DC 变换器，基于系统传递函数推导出解耦矩阵来解除闭环控制时移相角与占空比之间的耦合关系。但是由于用稳态增益替代传递函数近似得到的解耦矩阵存在误差，引入相应的解耦矩阵会增加系统的不稳定性，为此本文提出将模型划分为不同的子模块再分别解耦以降低解耦的难度。

本文针对DC-DC LED 驱动电路，提出一种逆系统解耦双电流环控制方法。在建立系统大信号平均模型的基础上，采用双电流环控制结构，将模型分解为4 个子模块：输入扰动模块、负载扰动模块、内电流环模块和外电流环模块。通过前馈解耦，消除输入电压扰动和负载扰动对输出电流的影响，消除内电流环和外电流环的交叉耦合，然后基于逆系统理论对内电流环和外电流环进行解耦，并补偿为一阶积分子系统，使得内电流环和外电流环的动态特性控制成为互不影响的独立环路，简化控制器的设计。本文以Boost 型LED 驱动电路为例，设计其逆系统解耦双电流环控制系统，并对控制系统进行仿真和实验结果验证。

1 Boost 型LED 驱动电路主电路的大信号平均模型

考虑电感和电容寄生电阻的Boost 型LED 驱动电路主电路如图1 所示。其中：Vin表示输入直流电压；L 表示电感；iL表示电感电流；rL表示电感的等效串联电阻ESR（equivalent series resistance）；vLr表示电感及其寄生电阻两端的电压；Q 表示功率开关管；D 表示二极管；C 表示电容；iC表示电容电流；rC表示电容的等效串联电阻；ZLED表示负载阻抗；vo表示输出电压；io表示输出电流。

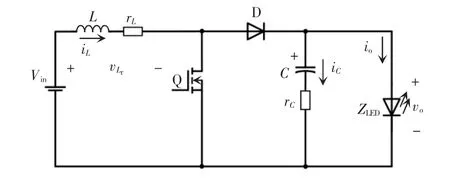
图1 Boost 型LED 驱动电路主电路Fig.1 Main circuit of Boost LED driver

假设系统工作在电感电流连续导通模式CCM（continuous conduction mode）下，采用三端PWM 开关器件模型法[20]得到CCM 下Boost 型LED 驱动电路主电路的大信号平均模型电路方程为

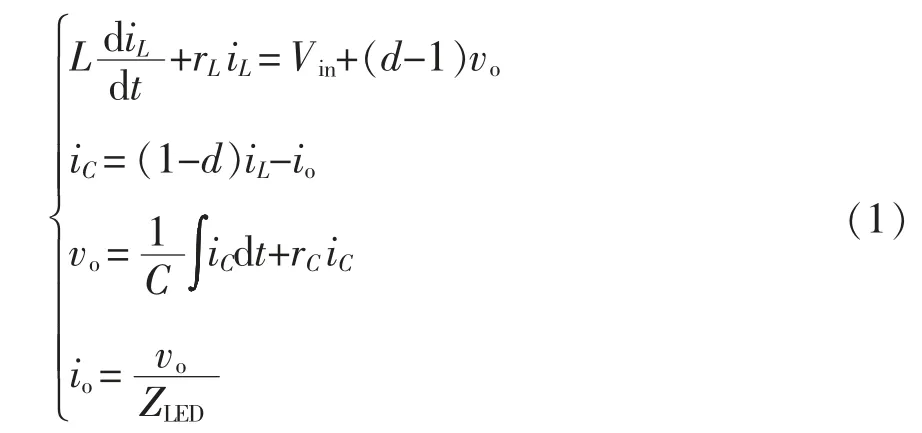
式中，d 为开关管Q 的占空比。将式（1）进行拉普拉斯变换得到

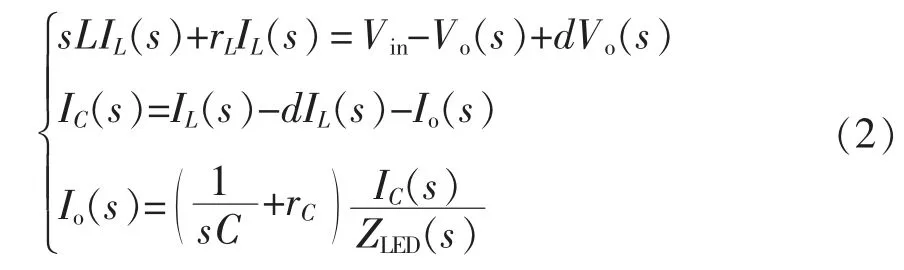
CCM 下Boost 型LED 驱动电路主电路的大信号平均模型方框图如图2 所示。

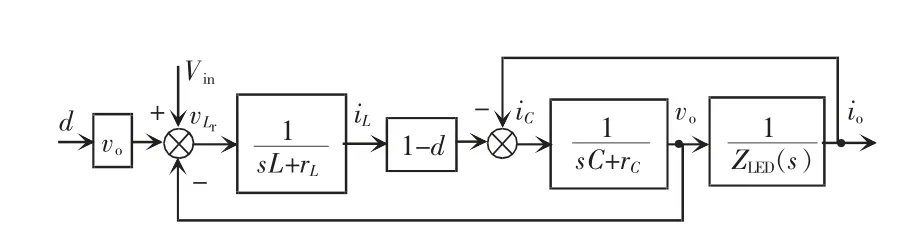
图2 CCM 下Boost 型LED 驱动电路主电路的大信号平均模型方框图Fig.2 Block diagram of large-signal averaged model of main circuit of Boost LED driver in CCM

2 Boost 型LED 驱动电路双电流环控制系统的逆系统解耦控制

逆系统方法[15]属于反馈线性化方法，针对给定的系统，将被控对象补偿成伪线性系统，然后利用线性系统理论对伪线性系统进行控制设计。假设对于给定非线性系统Σ∶y=θu，其中θ 为算子，输入变量为u，输出变量为y。若存在另一个系统为算子，输入变量为φ，输出变量为u，系统Σα的初始条件和系统Σ 相同，选取φ=y（α），并且算子满足

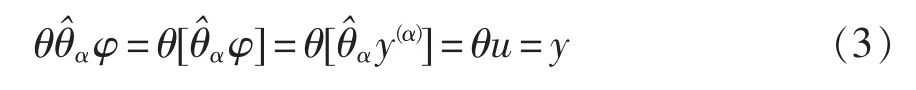
则称系统Σα为系统Σ 的α 阶积分逆系统。根据式（3）可知，由复合算子所表示的系统相当于α 阶积分器串联型系统y=s-αφ。因此逆系统串接在原系统之前构成的复合系统是伪线性系统。伪线性系统的结构如图3 所示。显然，将系统Σ 补偿成为伪线性系统后，便可用各种线性控制理论来完成闭环控制系统的设计。

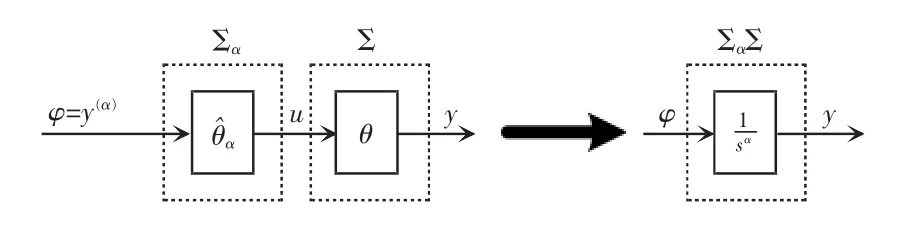
图3 α 阶积分逆系统线性化结构示意Fig.3 Schematic of linearization structure of α-order integral inverse system

由于LED I-V 曲线的非线性特性，为了精确地控制LED 输出电流，本文采用双电流环控制结构，即以iL为输出变量的内电流环和以io为输出变量的外电流环。由图2 的模型可见，电感电流iL和输出电流io之间存在交叉耦合关系。在此采用逆系统方法来进行解耦控制，使系统变为2 个相互独立的子系统。Boost 型LED 恒流驱动电路双电流环逆系统解耦控制系统结构框图如图4 所示。

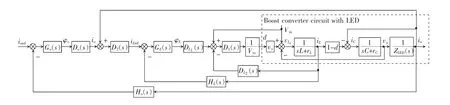
图4 Boost 型LED 恒流驱动电路双电流环逆系统解耦控制系统结构框图Fig.4 Structural block diagram of double-current loop inverse-system decoupling control system for constant-current Boost LED driver

图4 中的控制系统可分解为4 个子模块：输入扰动模块、负载扰动模块、内电流环和外电流环。Go（s）和GL（s）分别表示外电流环和内电流环的线性反馈控制器，Ho（s）和HL（s）分别表示外电流环和内电流环的反馈环节，Do（s）和分别表示外电流环和内电流环逆系统解耦器，D1（s）、D2（s）分别表示输入扰动和负载扰动前馈解耦器。通过前馈解耦，D1（s）可以消除输入电源引起的扰动影响，D2（s）可以消除负载扰动的影响，Do（s）和可以消除内电流环和外电流环之间的交叉耦合关系，使Boost 型LED 驱动电路的扰动控制、外电流环动态特性控制以及内电流环动态特性控制成为相互独立的过程，简化了控制器的设计。对输入扰动和负载扰动的前馈解耦器设计方法在多篇文献中已有研究[21-22]，在此不再赘述，下面将着重论述采用逆系统方法求解内电流环被控对象和外电流环被控对象的线性化解耦子模块的过程。

2.1 内电流环被控对象的逆系统

对于内电流环被控对象而言，其状态方程和输出方程为

式中：状态变量x1=iL；控制变量u1=vLr；输出变量y1=iL。输出方程两边对时间t 求导数，可以得到

Det（A）=1/L≠0，rank（A）=1，矩阵A 为非奇异矩阵，内电流环被控对象状态方程的相对阶为α=1，等于系统状态变量的维数n=1，从而内电流环被控对象是一阶可逆的。

选取新的变量φL=作为逆系统的输入变量，原系统的控制变量vLr作为逆系统的输出变量，构造出内电流环被控对象的逆系统为

将式（7）进行拉普拉斯变换，得到具有状态反馈的逆系统结构为

假设所有测量值与真实值相等，则内电流环被控对象的开环传递函数为IL（s）/ΦL（s）=1/s。内电流环被控对象通过逆系统方法线性化解耦为一阶线性积分系统IL（s）=s-1ΦL（s）。通过设计合适的控制器GL（s），使iL实时快速地跟踪iLref的变化，则内电流环可等效为IL（s）/ILref（s）=1/H2（s）。

2.2 外电流环被控对象的逆系统

对于外电流环被控对象，控制变量为u2=iC，输出变量为y=io。重新定义Φo（s）=sIC（s）为新的输入变量，IC（s）为输出变量，得到外电流环被控对象逆系统，即

如果所有测量值与真实值相等，则外电流环被控对象的开环传递函数为Io（s）/Φo（s）=1/s。外电流环被控对象通过逆系统方法线性化解耦为一阶线性积分系统Io（s）=s-1Φo（s）。

因此，Boost 型LED 恒流驱动电路双电流环逆系统解耦控制方法所构造的伪线性系统在物理上是可实现的，如图5 所示。对原系统的控制问题转化为对具有标准形式的伪线性系统控制问题，可以根据设计目标，按线性系统的设计理论来完成所要 求的控制系统。

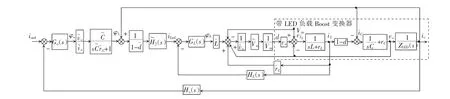
图5 Boost 型LED 恒流驱动电路双电流环逆系统解耦控制方框图Fig.5 Block diagram of double-current loop inverse-system decoupling control for constant-current Boost LED driver

3 控制器设计

由以上推导结果可以看出，经加入逆系统解耦环节，消除了外电流环和内电流环的交叉耦合，以及输入电源和负载电流的干扰耦合。解耦后，外电流环和内电流环的开环传递函数均为一阶纯积分环节1/s。下面将对外电流环控制器Go（s）和内电流环控制器GL（s）进行设计，可等效为对一阶积分系统设计控制器。

根据线性二次型调节器LQR（linear quadratic regulator）理论，可以证明对于能控线性定常系统状态方程为

式中：状态变量x∈Rn；输入变量u∈Rm，没有约束；A、B 为维数适当的常数矩阵。定义性能泛函J 为

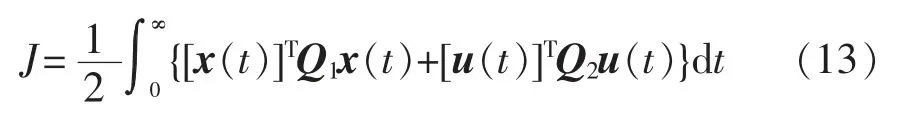
式中：Q1为半正定常数矩阵；Q2为正定常数矩阵。则存在唯一的最优控制

式中，P 为n×n 维对称正定常数矩阵，满足Riccati矩阵代数方程，有

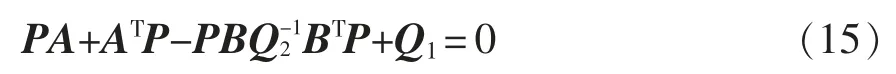
一阶积分系统的状态方程和输出方程为

式中：φ 为控制变量；h 为反馈系数。显然这是一个完全能观能控的线性定常系统，近似最优控制存在。采用P、PI 调节器的控制系统结构框图如图6所示。

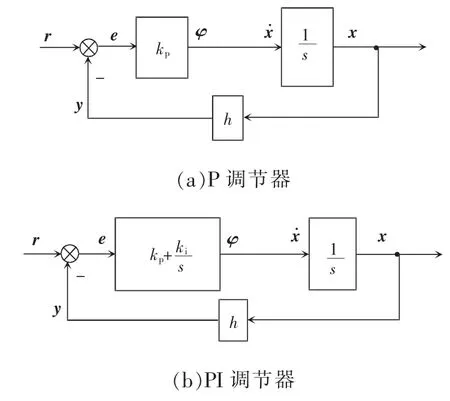
图6 P、PI 调节器的控制系统结构框图Fig.6 Structural block diagram of control system with P and PI regulators

3.1 LQR 最优P 调节器

图6（a）为采用P 调节器的一阶积分最优控制系统，一阶积分线性系统偏差量为e=r-y，选取状态变量x=e，输入变量u=φ 可以将输出调节器问题转化为等效的状态调节器问题，则式（16）中的状态方程变为

联立式（12）和式（17），得A=[0]，B=[-h]。由式（17）得系统为一阶系统，可取加权矩阵Q1=[q1]≥0，Q2=[q2]>0，定义二次型性能指标为

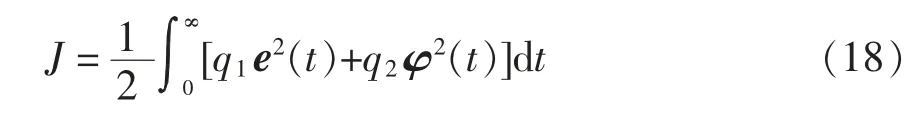
优化的目标是要求在式（17）约束下，寻求u*使目标函数为最小，选取P=[p]≥0，代入式（15）解得，则最优控制为

该调节器是P 型调节器u=kpe，则0。LQR 最优P 控制系统的闭环传递函数为一阶惯性环节

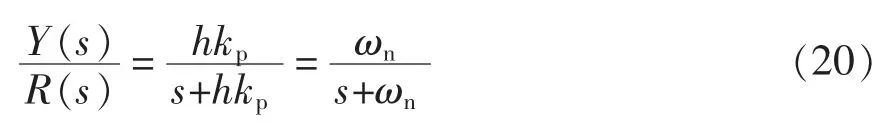
式中，ωn=hkp为自然频率。闭环系统的特征根为s=-hkp＜0，因而闭环系统是渐近稳定的。

3.2 LQR 最优PI 调节器

P 调节器可使系统具有较好的动态性能。为更好地实现多项式输入的无静差跟踪，应使系统的开环传递函数具有一定的积分环节个数。图6（b）为采用PI 调节器的一阶积分最优控制系统，选取状态变量，输入变量，则式（16）中的状态方程变为

3.3 ITAE 最优调节器

除上述LQR 最优控制方法外，也可以采用其他优化设计方法设计控制器的参数，例如ITAE（integral of time and absolute error）优化方法。带前置滤波器的阶跃响应ITAE 最优PI 调节器如图7 所示。

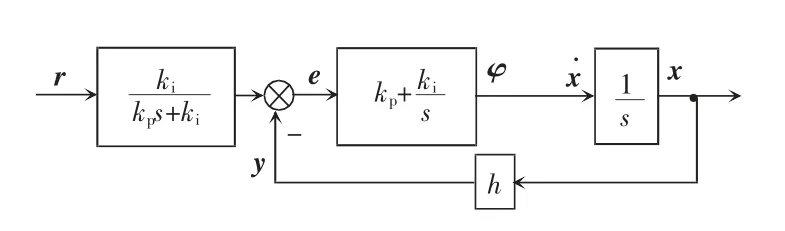
图7 带前置滤波器的阶跃响应ITAE 最优PI 调节器Fig.7 ITAE optimal PI regulator with prefilter step response

ITAE 性能指标为

当采用ITAE 指标时，对于阶跃响应，一阶闭环系统式（20）的最优特征多项式为s+ωn，因而LQR 最优P 调节器同时也是ITAE 准则下的最优调节器。对于斜坡输入而言，基于ITAE 指标的二阶有零点闭环系统式（24）的最优特征多项式为s2+3.2ωns+。对于阶跃响应，二阶无零点闭环系统的最优特征多项式为s2+1.4ωns+，而二阶有零点闭环系统式（24）阶跃响应的ITAE 性能指标要达到最小，需在系统输入端接入前置滤波器（如图7 所示），以抵消闭环传递函数的零点，从而具有预期的最优ITAE指标。

4 仿真和实验验证

本文针对所设计的Boost 型LED 恒流驱动电路逆系统解耦控制系统在Matlab/Simulink 平台上进行数值仿真，并搭建实验样机进行实验验证。Boost 型变换器的主电路参数为：输入电压Vin=5 V，电感L=100 μH，电感寄生电阻rL=0.005 Ω，电容C=470 μF，电容寄生电阻rC=0.005 Ω，开关频率fs=50 kHz。负载为5 个350 mA 的白光LED 串联得到的白光LED灯板，输出电流参考值为ioref=350 mA。

在时域范围内，系统响应速度的快慢由闭环系统的无阻尼振荡频率ωn的大小决定。在频域范围内，对于任意阶次的控制系统，其阶跃响应的速度和闭环系统的带宽频率ωb成正比。一阶和二阶闭环系统ωn与ωb的关系见文献[16]。在实际的DC-DC变换器设计过程中，为了改善系统的动态性能，并且保持其对高频噪声的抑制水平，对于双闭环控制结构，内环带宽受到开关频率的限制，要求内环带宽频率要远远小于开关频率，而外环带宽频率要远远小于其内环带宽频率[23]。设计该系统内电流环采用PI 控制器，反馈网络参数为HL（s）=1，由式（24）得，内环选取ωn2=7×103rad/s，则kp2=104，ki2=5×107，外电流环采用P 控制器，反馈网络参数为Ho（s）=1，由式（20）可得kp=ωn/h，外环选取ωn1=500 rad/s，则kp1=500。

图8 给出了在负载为5 个LED 的情况下，t=0.1 s 时输入电压从5 V 跳变到12 V，系统动态响应仿真波形。可以看出在输入电压为5 V 时，输出电流为参考值350 mA，当输入电压发生跳变时，输出电流的调节时间为ts=1.5 ms，即当输入电压从5 V跳变到12 V 时，输出电流经过1.5 ms 后重新回到参考值350 mA。

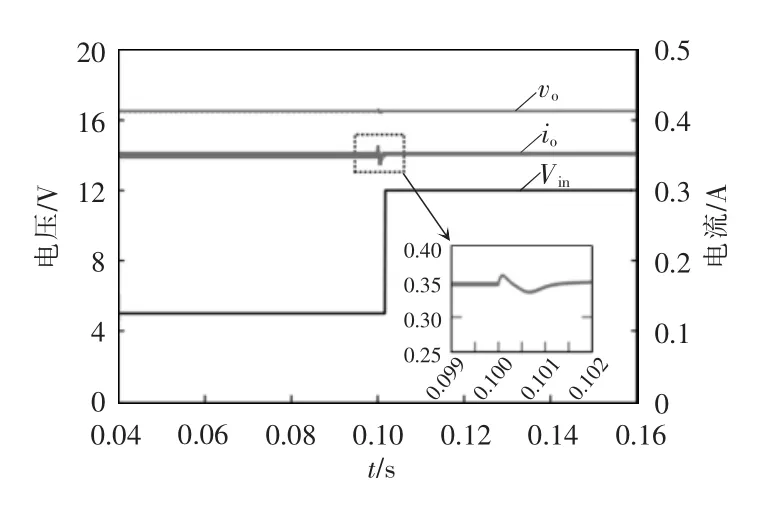
图8 输入电压跳变仿真波形Fig.8 Simulation waveforms under input voltage disturbances

图9 给出了在Vin=5 V 的情况下，且在t=0.1 s时负载LED 个数从3 个增加到5 个时，系统动态响应仿真波形。从图9 可以看出，3 个LED 时输出电流为参考值350 mA。当负载发生跳变时，因为负载LED 具有二极管特性，5 个白光LED 的开启电压为15 V，而3 个白光LED 的稳定电压仅为10 V，所以在跳变瞬间负载LED 两端的电压未达到开启电压值，此时没有电流通过，输出电流降为0 A。在逆系统解耦控制方法和最优控制器的作用下，输出电流经过4 ms 的调节时间重新回到参考值350 mA。根据图8、图9 可以看出，输入电压跳变和负载跳变的仿真结果表明系统具有较快的响应速度和较短的调节时间。

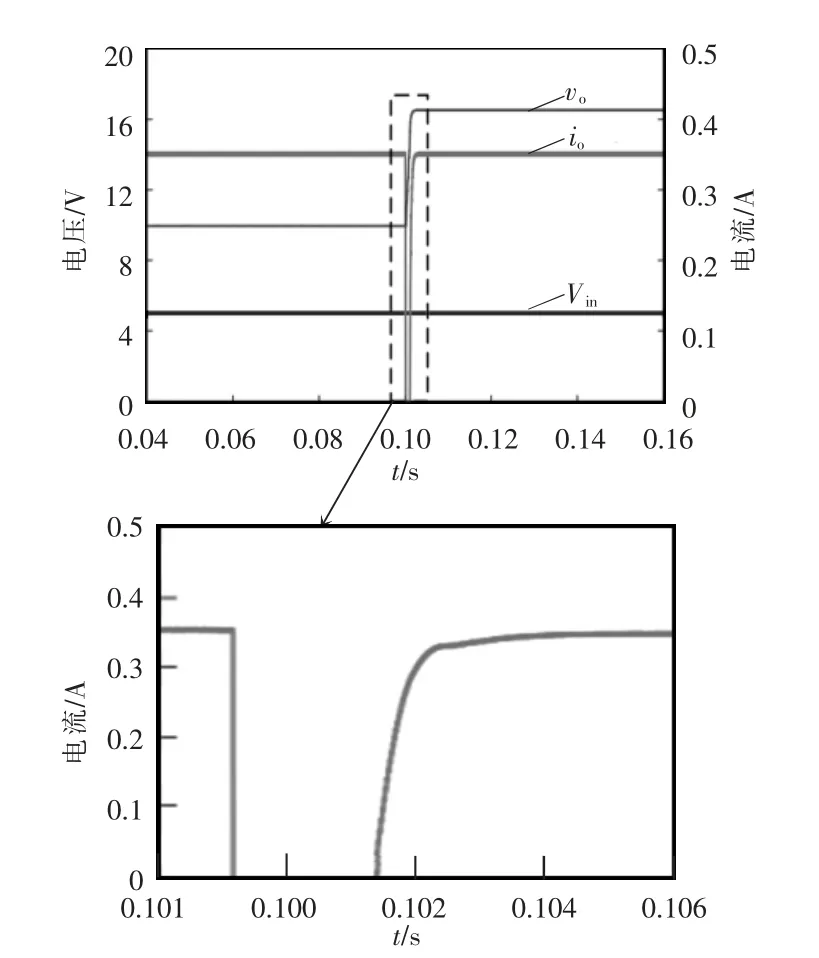
图9 负载跳变仿真波形Fig.9 Simulation waveforms under load disturbances

为了进一步验证所提逆系统解耦双电流环控制方法的正确性和有效性，搭建了一台Boost 型LED 恒流驱动电路的实验样机，如图10 所示。

图10 Boost 型LED 恒流驱动电路实验样机Fig.10 Experimental prototype for constant-current Boost LED driver

其中包括GW Instek PSB-1400M 多量程直流电源、Boost 变换器、TMS320F2812 数字信号处理器（DSP28 12）、LV25-P 霍尔电压传感器和HCS-LSP-06A 闭环霍尔电流传感器构成的采样电路以及Tektronix TPS 2024B 四通道数字存储示波器。Boost变换器的开关管选用IRF540N，栅极驱动电路选用TLP 250 驱动芯片。实验样机的参数和Simulink 仿真参数一致。控制系统的采样周期选取和开关周期一致，即采样周期T0=20 μs。控制算法离散化后占空比d（k）推导过程为

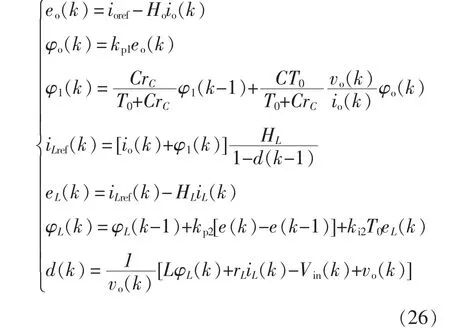
图11 为输入电压从5 V 跳变到12 V 时，Vin、io和vo的实验波形。可以看到输出电流平均值能稳定在参考值350 mA 处，实现了LED 的恒流驱动，在输入电压跳变的瞬间，输出电流几乎没有波动。

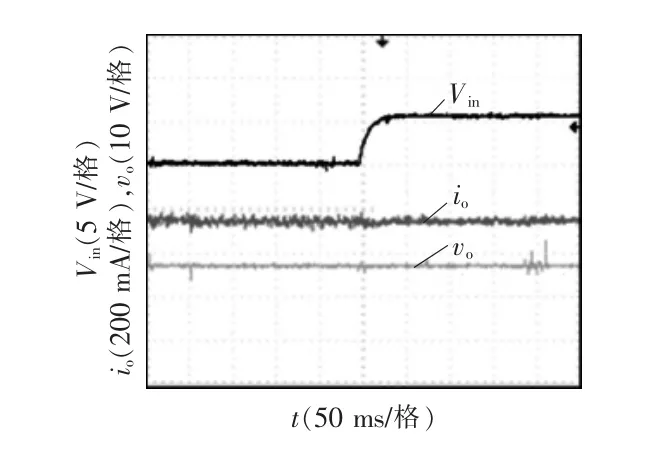
图11 输入电压跳变时的实验波形Fig.11 Experimental waveforms under input voltage disturbances

图12 给出了LED 灯板上的灯珠由3 个变成5个时Vin、io和vo的波形。从图12 中可以看出，输出电流先降为0 A，然后在逆系统解耦控制器的作用下调节回参考值350 mA，这表明所提控制方法具有良好的抗干扰能力。实验结果和仿真结果基本一致，表明所提出的逆系统解耦双电流环控制方法的正确性和有效性。

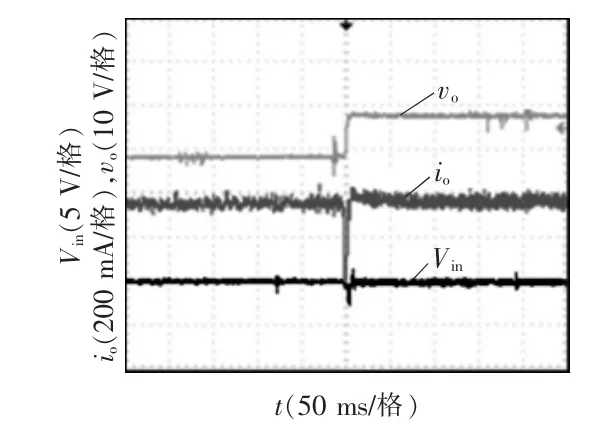
图12 负载跳变实验波形Fig.12 Experimental waveforms under load disturbances

以上实验是基于电学角度对所设计的Boost 型LED 恒流驱动电路进行验证。从光学角度来说，LED 的光通量主要由流经LED 的正向电流决定，流过LED 的电流和LED 的光通量的比值是非线性的[24]。光学实验测试系统如图13 所示，用半径为0.5 m 的积分球和CMS-2S 快速光谱分析仪测量LED的光通量和光效。变换器负载为5 个白光LED，输入电压以0.5 V 间隔从5 V 开始递增到12 V，测量LED光通量和光效的变化，测量结果如表1 所示。由表1 可知，LED 光通量最小值为504.46 lm，最大值为509.43 lm，其标准差为1.218 lm，说明LED 光通量较为稳定。光效的最小值为84.42 lm/W，最大值为84.90 lm/W，其标准差为0.138 lm/W，说明LED 光效的波动范围较小，稳定性高。

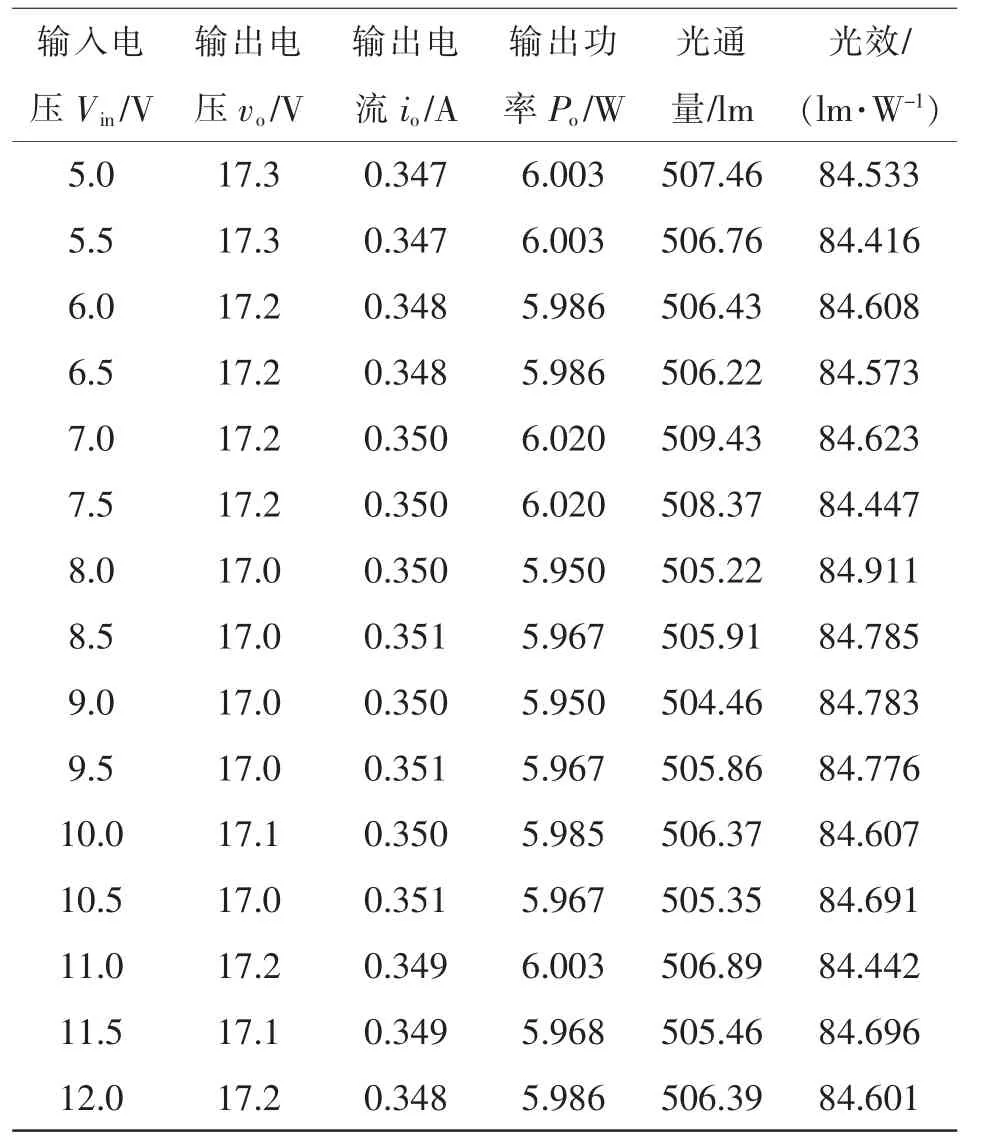
表1 LED 光通量和光效测试数据Tab.1 Test data of LED luminous flux and luminous efficiency

图13 光学实验测试系统Fig.13 Test system for optical experiment

以上实验结果从电学和光学角度验证了所设计Boost 型LED 恒流驱动电路是稳定和有效的。

5 结论

本文对带LED 负载的DC-DC 变换器，提出了一种逆系统解耦双电流环控制方法，以Boost 型LED恒流驱动电路为例阐述了算法的实现过程，通过搭建其实验样机，从电学和光学两个角度验证了所提控制方法的正确性和有效性，得到以下结论：

（1）通过串级解耦、前馈解耦以及状态反馈解耦等多种解耦方法相结合，消除了电源扰动和负载扰动对系统的影响，在控制系统设计过程中无须对LED 建立等效电学模型，有效避免了LED 等效模型建立不够准确的问题。

（2）所建立的系统模型为大信号模型，系统的非线性乘积项没有被忽略，保证了系统模型的准确性及在大信号扰动下的稳定性。

（3）采用逆系统理论进行解耦控制，将内电流环和外电流环分别与逆系统解耦补偿器共同组成两个独立的一阶积分子系统，消除系统内环和外环之间的非线性强耦合关系，简化了控制器的设计。