屏栅电源新型双全桥拓扑的模型预测控制

安昌祖，张蕊萍，翟 浩，董海鹰，3

（1.兰州交通大学自动化与电气工程学院,兰州 730070；2.兰州空间技术物理研究所，兰州 730000；3.兰州交通大学新能源与动力工程学院,兰州 730070）

伴随我国大功率离子电推进技术的快速发展，离子推进器电源处理单元PPU（power processing unit）的功率等级越来越高，高效率、高功率密度的屏栅电源已是PPU 发展的目标，屏栅电源作为PPU 的核心部件显得尤为重要，而屏栅电源的控制设计是实现高电压、大功率的关键。因此，研究屏栅电源的控制对我国大功率离子电推进技术的快速发展具有重要意义[1-2]。

目前，国际上根据应用环境的不同，对屏栅电源的改进主要在拓扑结构和控制方法上。Astrium公司的离子推力器MULTI-RANGE 屏栅电源由两组变换器组成，主变换电路采取谐振式DC/DC 拓扑，次变换电路采用推挽式拓扑，电压调节能力有限，拓扑设计为单控制回路，不能控制系统电流[3-4]；“深空一号”推力器屏栅电源采用非谐振全桥电路，能满足宽动态范围和高功率需求，但热耗大，会降低PPU 效率[5-6]；国内研制的LIPS-200 离子推力器屏栅电源是由一组全桥硬开关DC/DC 变换电路构成，在LIPS-200 推力器屏栅电源的基础上形成下一代LIPS-300 推力器，在效率方面与国外先进水平基本一致[7]，但输出电压宽范围调节还需进一步研究。目前针对屏栅电源的控制通常采用PID 电压、电流双闭环[8]，此控制方法在实际工程应用中控制不稳定，受系统建模影响大，难以克服因负载等因素变化带来的干扰，因此，需要设计一种控制精度高、抗干扰能力强的控制方法。

本文针对屏栅电源宽范围电压输出的技术需求，在原全桥拓扑的基础上，提出新型双全桥拓扑，其创新性在于利用双全桥中的功率变压器副边串并联运行，实现输出电压宽范围调节，采用基于模型预测控制MPC（model predictive control）的双闭环控制方式[9]，实现输入电压宽范围条件下输出电压稳定宽范围输出。

1 变换器拓扑结构及工作原理

1.1 变换器拓扑结构

屏栅电源新型双全桥拓扑如图1 所示，电力场效应管A1～A4和变压器T1构成全桥电路A 桥，电力场效应管B1～B4和变压器T2构成全桥电路B 桥，A 桥和B 桥经副边两个整流桥整流，因副边两个整流桥的相邻桥臂作用相同，所以可将拓扑简化为图1 所示的三组桥臂组成整流桥。此拓扑的特点是实现T1、T2副边并联和串联两种运行模式，移相控制时两变压器副边处于串联模式，PWM 控制时两变压器副边处于并联模式，采用输入并联、输出串联和并联的结构能有效降低MOSFET 的电流应力和变压器的容量，最大限度满足推力器在可变推力条件下屏栅电源电压宽范围输出的要求[10-11]。

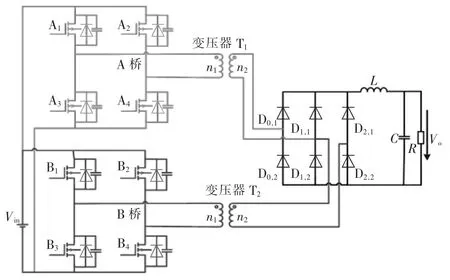
图1 新型双全桥拓扑Fig.1 Novel dual full-bridge topology

1.2 变换器工作模态

为了便于理解，假设开关管均为理想器件，两个变压器具有相同的匝数比。

模态a[t0，t1]：图2 为模态a 简化电路，A1、A4和B1、B4开通，输入电源开始传输到两个变压器副边，T1、T2原边电流Ip1、Ip2开始线性增加，二极管D0，1、D1，1、D1，2和D2，2导通并参与功率变换，直到D1，1、D1，2阴极电压高于阳极电压使得D1，1、D1，2反向截止。

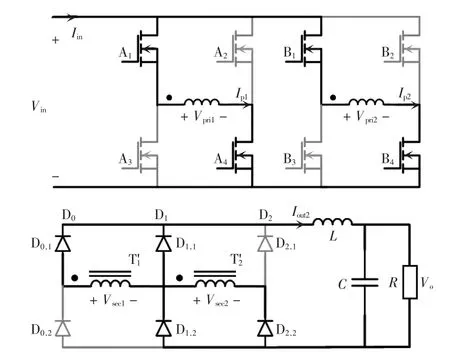
图2 模态a 简化电路Fig.2 Simplified circuit in mode a

模态b[t1，t2]：图3 为模态b 简化电路，电路运行时模态a 持续很短时间便进入模态b，A1、A4和B1、B4依然开通，此时D1，1、D1，2已关断，D0，1、D2，2依然开通将副边线圈串联起来，T1、T2原边电流持续上升，进入真正的串联模式，此时输出端口电压Vo为T1、T2端口电压之和，即

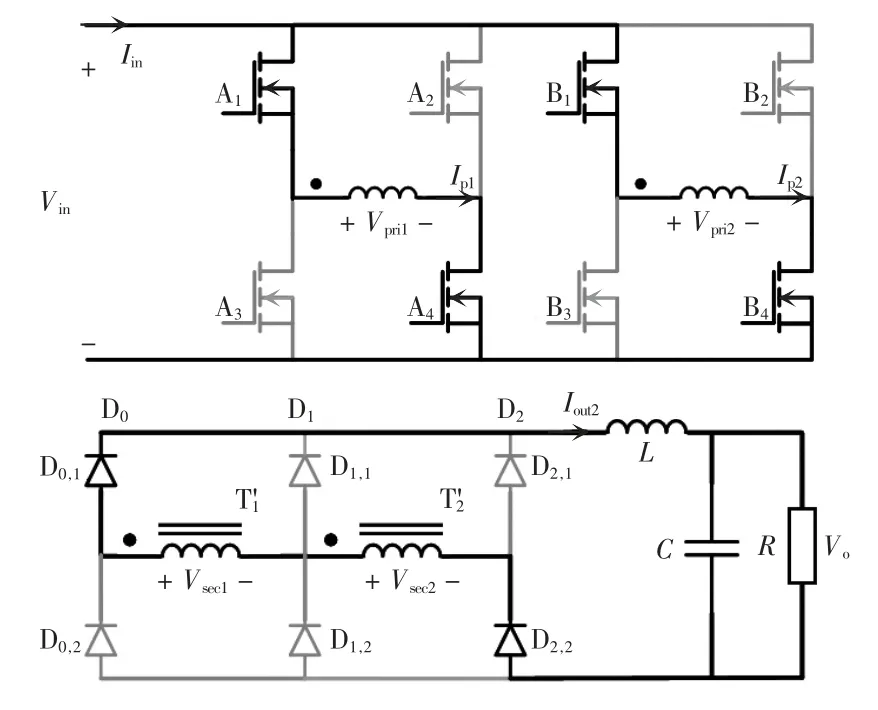
图3 模态b 简化电路Fig.3 Simplified circuit in mode b

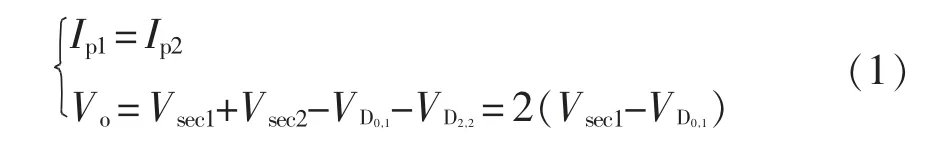
模态c[t2，t3]：简化电路如图4 所示A1、A4关断，B1、B4仍然开通，T1原边电流开始通过由T1的原边漏感L1k和电力场效应管寄生电容Coss组成的谐振回路而减小，T2仍然参与功率变换，因为T2副边电压保持不变、T1副边电压不断减小，导致二极管D0，1、D1，2反向截止，D1，1、D2，2仍然导通，此时处于串联到并联的过渡状态。电力场效应管寄生电容电压为

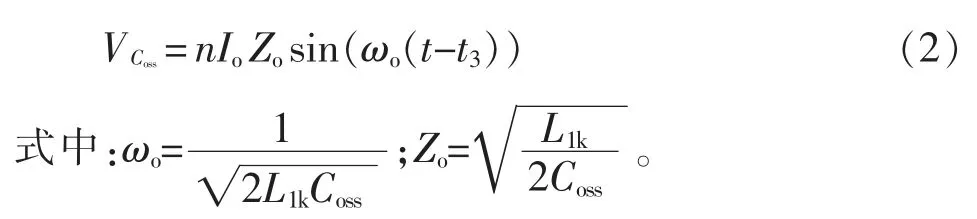
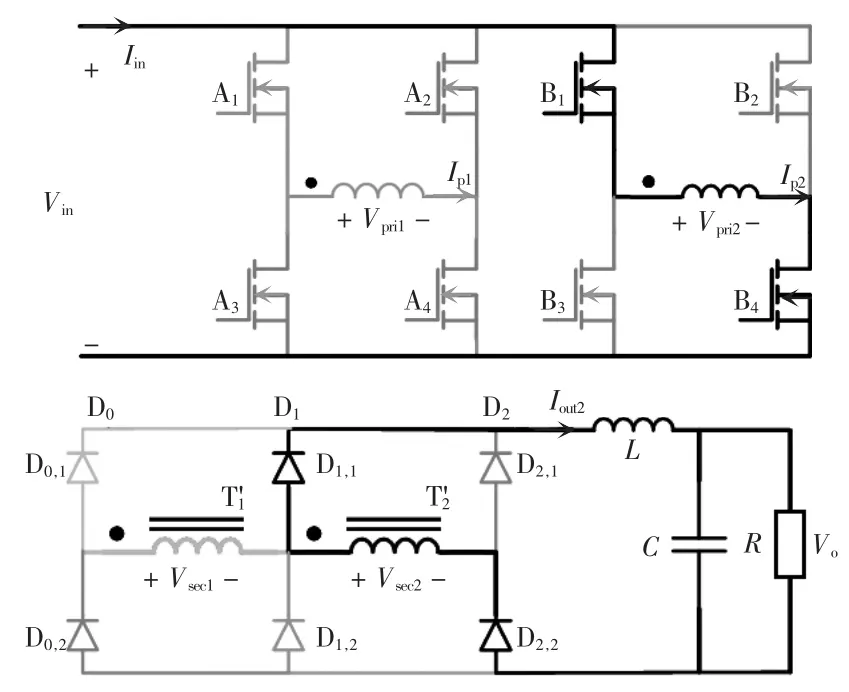
图4 模态c 简化电路Fig.4 Simplified circuit in mode c

模态d[t3，t5]：模态d 简化电路如图5 所示，B1、B4和A2、A3开通，当B1、B4开通时T2原边左正右负，A2、A3开通时T1原边左负右正，因此流过两个变压器原边电流方向相反，对应T1、T2副边线圈处于并联状态，此时流过D1，1的电流是D0，2、D2，2的2倍，输出端口电压等于T1、T2端口电压，即

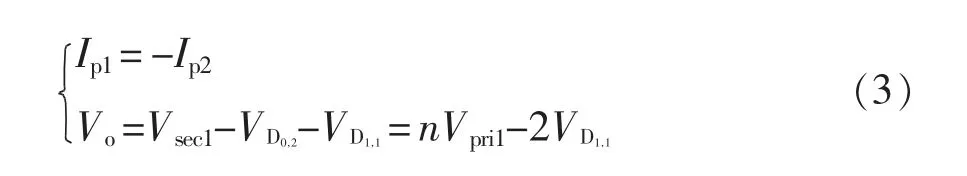
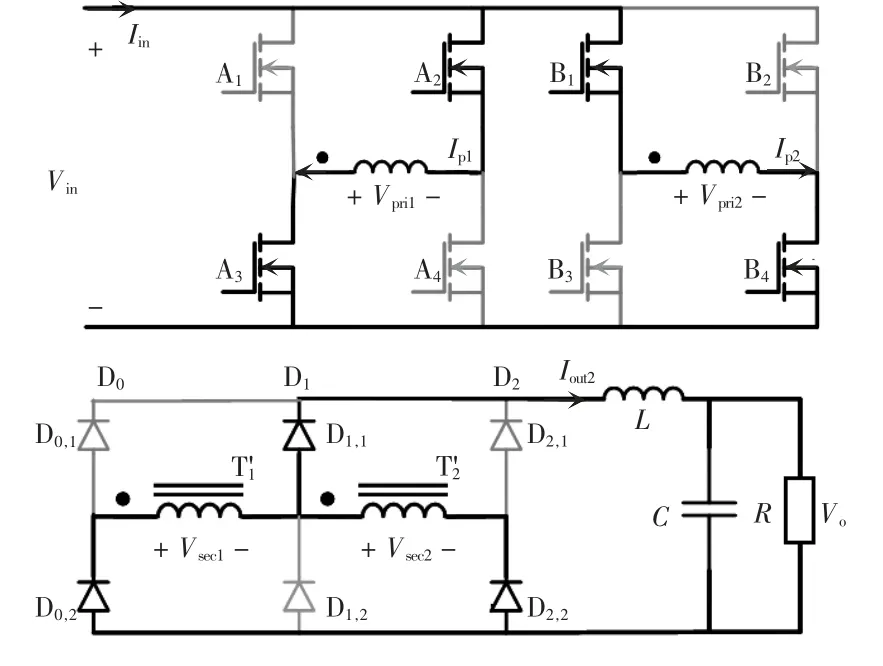
图5 模态d 简化电路Fig.5 Simplified circuit in mode d

模态e[t5，t6]：模态e 简化电路如图6 所示，A2、A3依然开通，B1、B4关断，此时T2与模态c 时的T1一样，电流通过谐振回路下降，T1参与功率变换，因为T1副边电压保持不变，T2副边电压不断减小，导致二极管D2，2关断，D1，1、D0，2开通，进入下一时刻，重复模态a～d 过程，但电流方向相反。

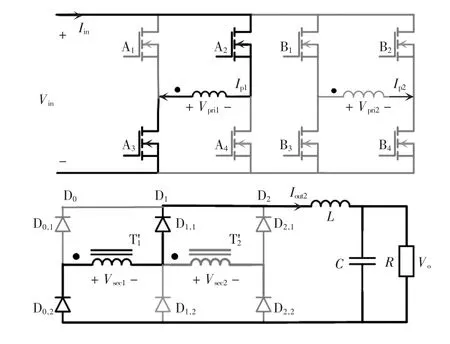
图6 模态e 简化电路Fig.6 Simplified circuit in mode e

对于新型双全桥拓扑，Vin和Vo的关系为

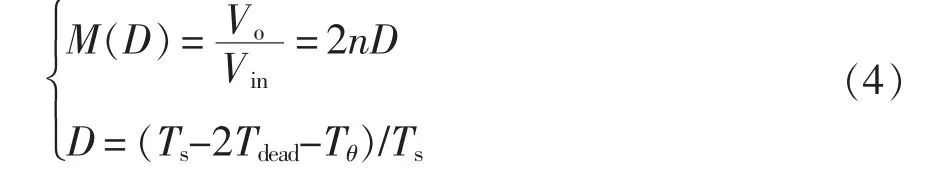
式中：Tdead为A1、A2之间的死区时间；Tθ为移相角θ时间；Ts为开关周期。

通过对模态a～d 的分析得出如图7 所示的时序波形，在不同移相角下输出电压Vo从到，假设二极管的导通压降为零，则输出电压最大值是最小值的2 倍，因此，当输出为高电压工况时，采用两变压器二次侧串联输出，以减小每个变压器容量；当输出为低电压工况时，采用两变压器二次侧并联输出，降低流过每个变压器的电流，实现宽范围输入电压条件下宽范围输出电压调节。

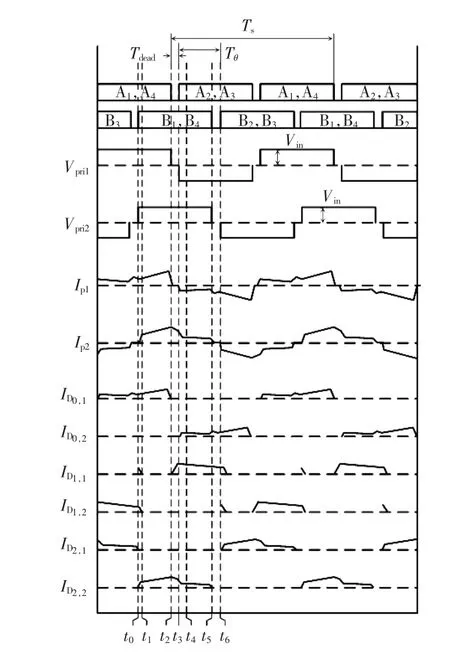
图7 时序波形Fig.7 Waveforms of time series

2 变换器的模型预测双闭环控制

图8 为输出并联PWM 模式控制结构，电流内环采取PID 控制，电压外环采取MPC 控制，电压外环MPC 控制器的输出是电流内环PID 控制器的给定，电流内环控制器输出PWM 信号给被控对象，因为是输出并联模式，则流过负载的电流是T1、T2的2 倍[12]。

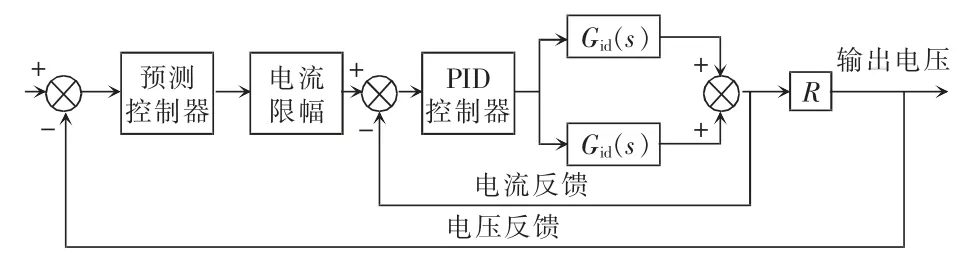
图8 输出并联PWM 模式控制结构Fig.8 Control structure in output parallel PWM mode

2.1 PID 电流内环设计

2.1.1 建立拓扑小信号模型

建立PWM 模式下输出端并联的拓扑小信号模型[13-14]，因为输出端并联，所以等效后T1、T2副边处于并联状态，A1～A4、B1～B4的开关周期为Ts，开通时间为ton，关断时间为toff，占空比d＜0.5[15-16]，图9 为电力场效应管导通和关断时的简化电路。

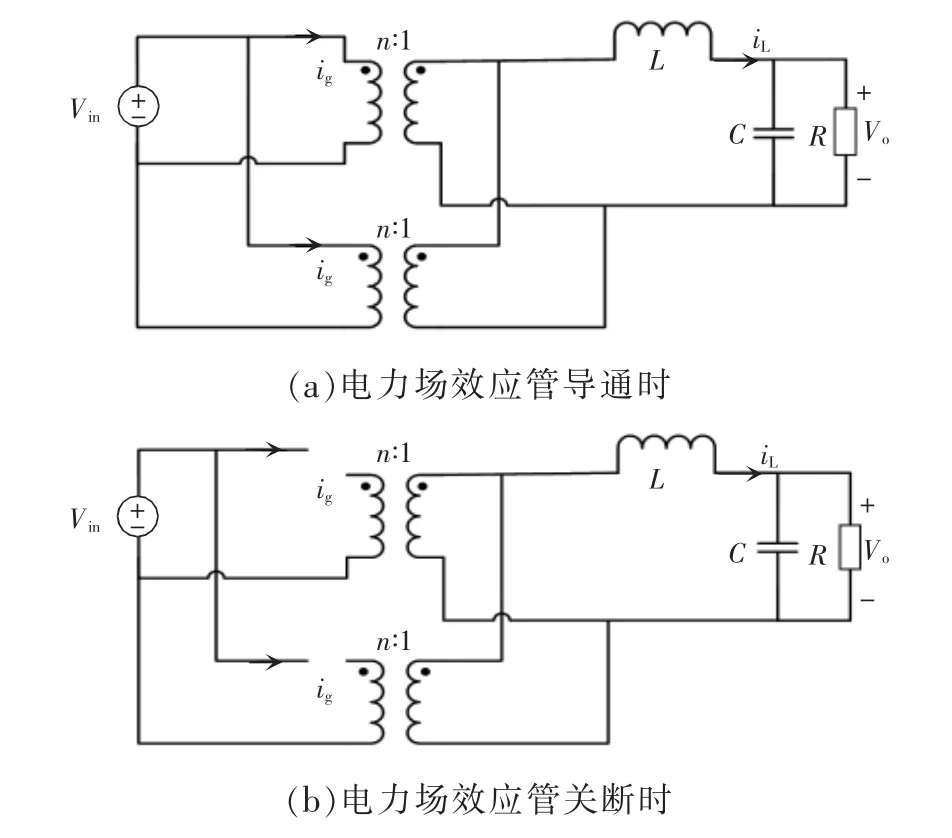
图9 变压器副边并联简化电路Fig.9 Simplified parallel circuit on secondary side of transformer

电力场效应管导通时满足

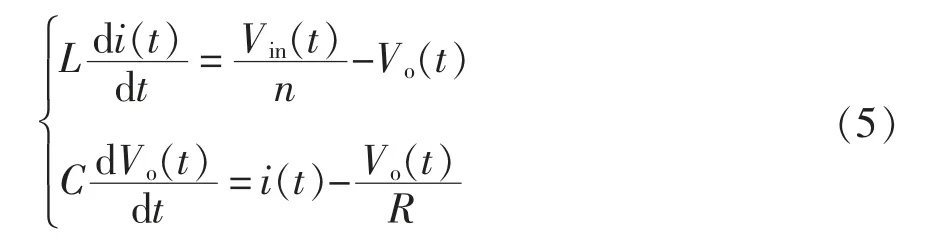
电力场效应管关断时满足

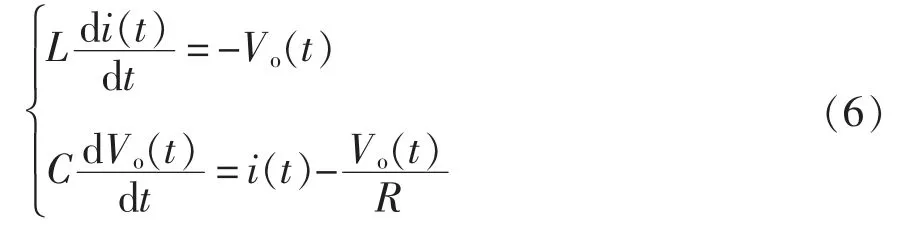
将状态变量在一个周期内求平均，简化得

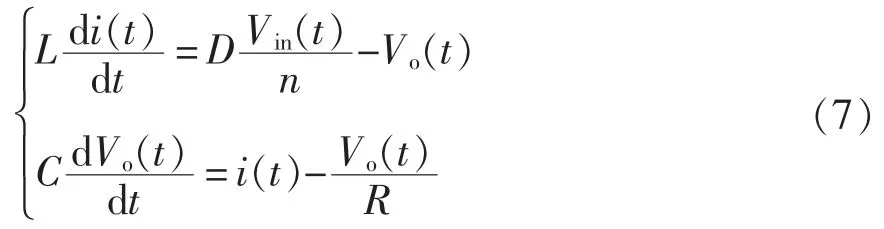
式（7）分别叠加电感电流、控制量、输出和输入电压、电容电压小信号扰动（用“^” 对应标注），忽略稳态分量、二次相分量和输入电压扰动，获得占空比扰动下的小信号方程为

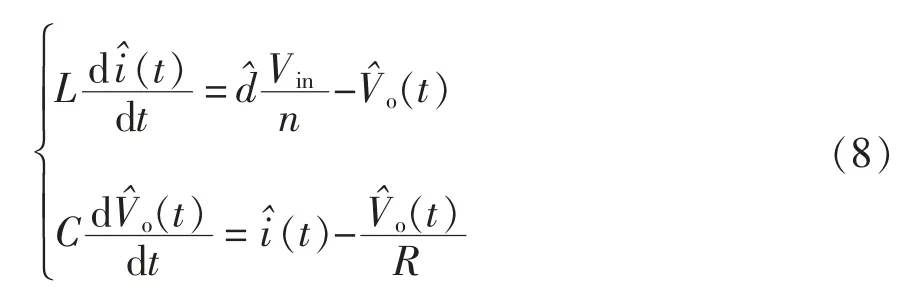
对式（8）拉氏变换获得频域方程为

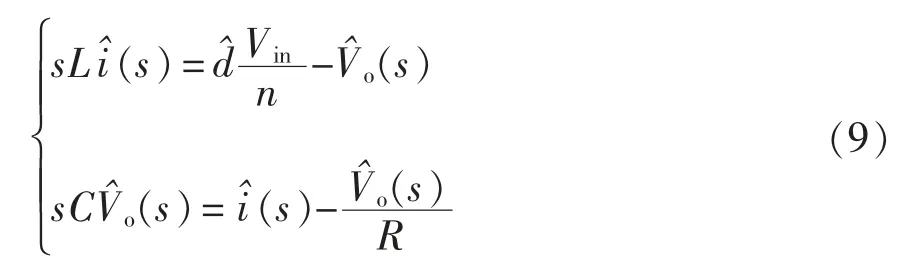
根据式（9）推导电压和电流与占空比的传递函数，分别为

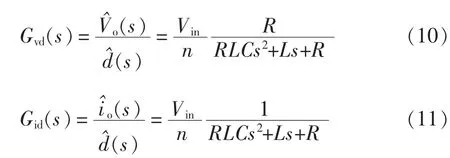
2.1.2 内环控制器

把新型双全桥拓扑电路参数代入式（11）可得

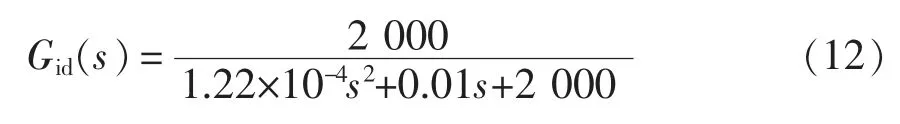
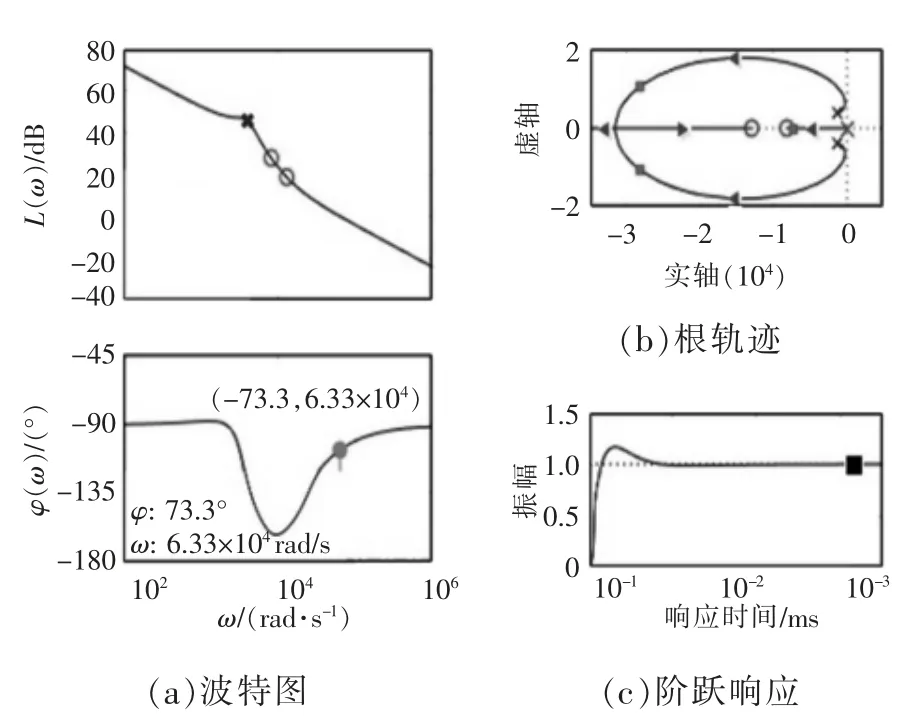
图10 补偿后的根轨迹、波特图和阶跃响应Fig.10 Root trajectory,Bode diagram and step response after compensation

此时电流内环控制器传递函数为

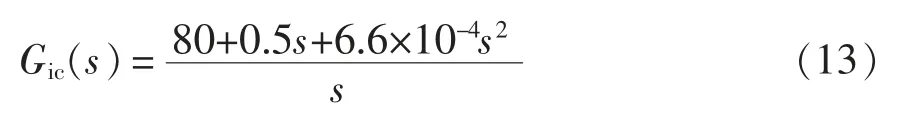
2.2 预测控制电压外环设计

2.2.1 预测模型

将电流内环作为MPC 的对象，则内环传递函数为[17]

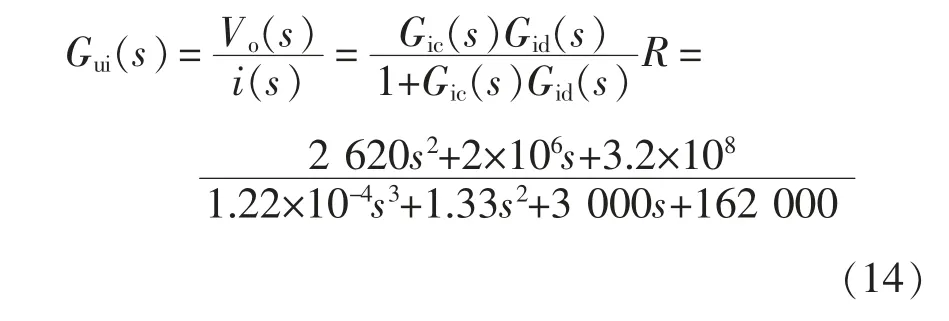
将上述传递函数转换为差分方程的形式[18]，即

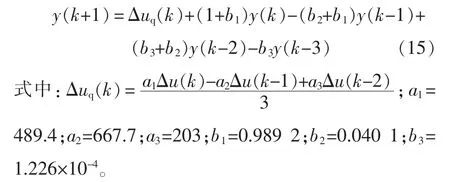
2.2.2 误差反馈校正

把k 时刻控制量u（k）作用于被控对象，即在被控对象的控制量上加了一个幅值为Δuq（k）的阶跃信号，根据式（15）的模型得出将来时刻的预测输出值y（k+1）。然而，在实际应用时会发生模型失配或外界干扰等问题，导致预测值与实际值之间存在一定的偏差，因此在求解k 时刻最优控制量时，先将k+1 时刻的实际值y（k+1）与k+1 时刻的模型预测值（k+1）相减构成输出误差[19-20]，即

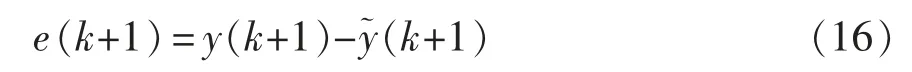
用误差反馈修正预测输出为

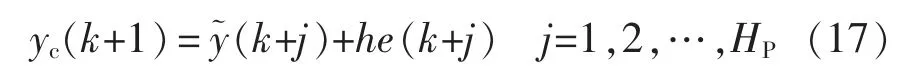
其矢量形式为

2.2.3 滚动优化

k+1 时刻的优化问题可表述为：从该时刻起的M 个控制量的变化量Δuq（k），…，Δuq（k+M-1），使控制对象在将来P 个时刻的输出正定，其中P>M。控制的最终目标是让实际输出电压以很小的超调量和调节时间跟随给定电压，并且使控制量的变化尽可能小，因此，在优化性能指标中加入约束关系可得[21-22]

对目标函数求最优解得到最优控制输出Δuq（k），根据滚动优化策略可知，只取最优解的第一步作用于被控对象[22]，则有

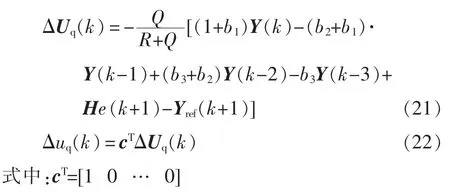
综上可知，MPC 是在k 时刻实施控制作用后，采集k+1 时刻的输出进行下一轮预测、校正、优化。因此，优化是在每一时刻建立一个新的局部优化目标，在线不断循环优化，得到最优控制量。

3 仿真与实验分析

为验证针对新型双全桥拓扑设计的MPC 双闭环控制方式的合理性，在Matlab 中建立功率电路、PID 双闭环控制电路和MPC 双闭环控制电路的仿真模型，并对比两种控制方法在突加给定、突减给定、突加负载、突减负载4 种工况下的控制效果以及串并联切换效果。

表1 为变换器参数。图11（a）为突加给定工况下PID 双闭环和MPC 双闭环输出值与给定值的对比，在0.025 s 时给定值从550 V 突然增加到850 V，MPC 仅0.005 s 就可以稳定在新的给定，PID 控制需要0.01 s 达到新的给定。图11（b）为突加给定工况下2 种控制方式的输出电流对比，可知给定突加后电流能在很短的时间内达到稳定。

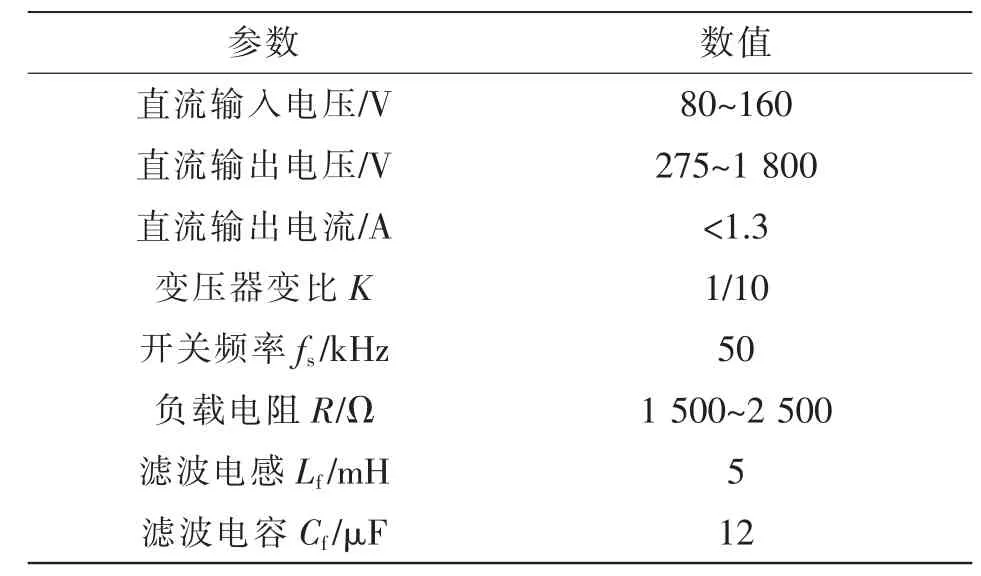
表1 变换器参数Tab.1 Parameters of converter

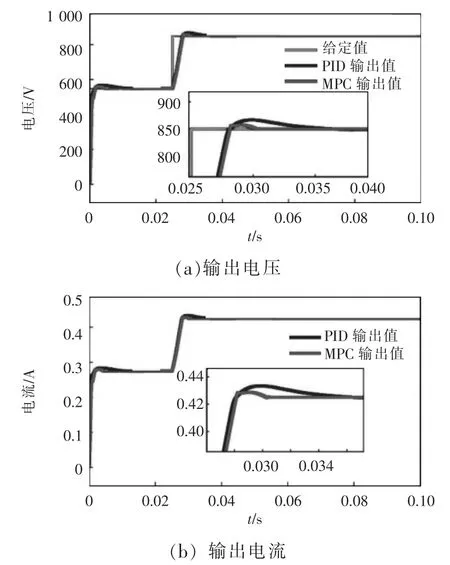
图11 突加给定Fig.11 Sudden increase in given value

图12（a）为突减给定工况下2 种控制方式控制输出电压与给定电压的对比，当给定电压突然减小，由于输出端并联电容导致输出电压不能快速跟踪给定，经过大约0.01 s 后稳定到给定值，可看出PID 控制下超调较大，MPC 控制下超调很小，图12（b）为突减给定工况下2 种控制方式控制输出电流对比。

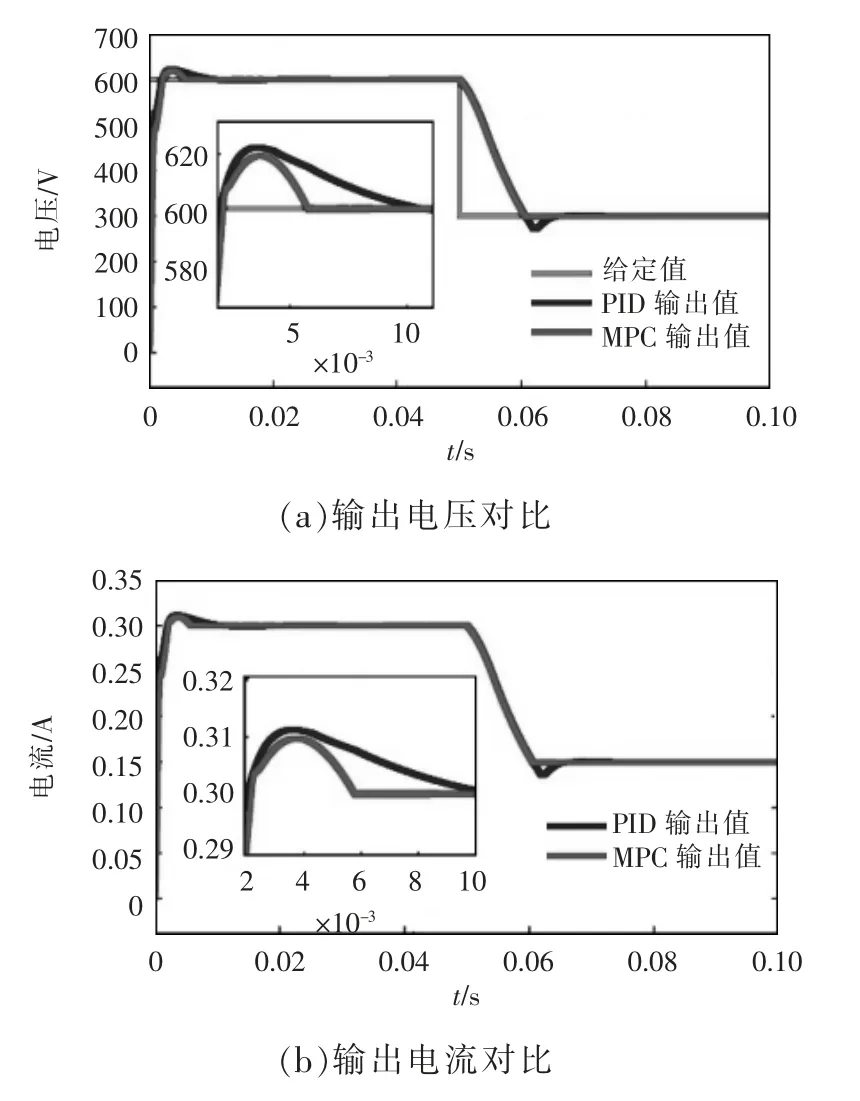
图12 突减给定Fig.12 Sudden decrease in given value

图13 为负载突然增加工况下2 种控制方式控制输出电压和电流对比，可知0.05 s 时负载突然增加，此时PID 控制输出电压和电流波形受负载突增影响产生向下的波动，经过0.004 s 后恢复到给定电压值，MPC 控制输出电流和电压在负载突增时所受影响很小，在极短的时间内恢复到给定值。

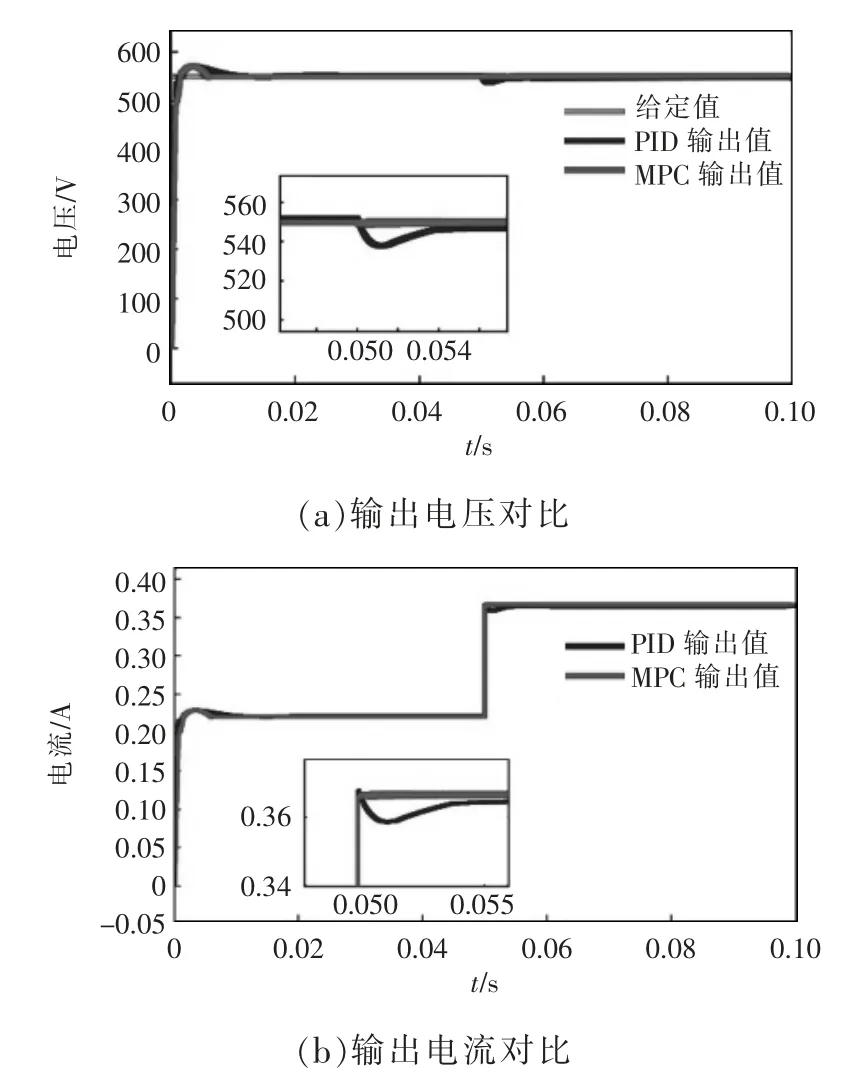
图13 突加负载Fig.13 Sudden increase in load

图14 为负载突减工况下2 种控制方式控制输出电压和电流对比，0.05 s 时负载突然减小，2 种控制方式控制输出电压和电流均发生波动，PID 控制下电压在0.005 s 内恢复到给定电压，MPC 控制下电压在0.002 5 s 内恢复到给定值，并且PID 控制下的超调明显大于MPC 控制下的超调。

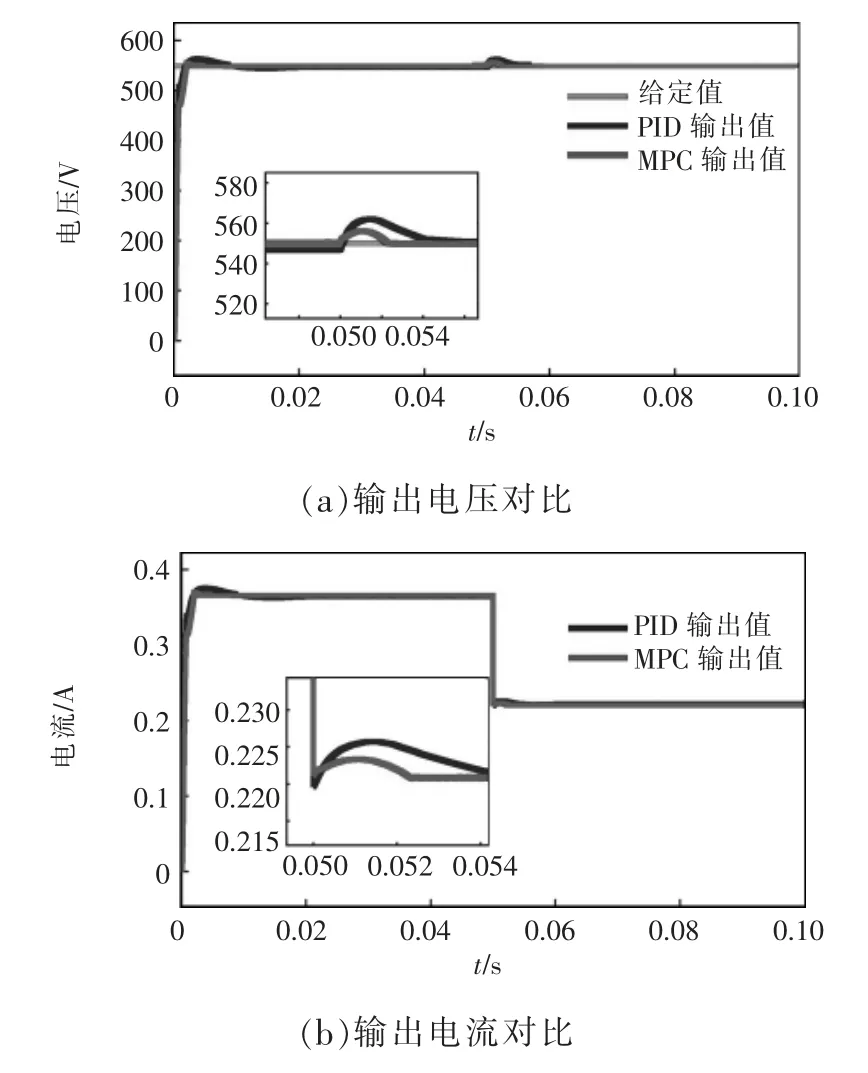
图14 突减负载Fig.14 Sudden decrease in load

图15 为输出串联和并联切换电压对比。因为变压器变比为1∶10，所以将切换点定为单个变压器最大输出电压900 V，由图15（a）可知在0.025 s 时给定电压由500 V 增加到1 600 V 经过切换点，由图15（b）可知在0.05 s 时给定电压由1 750 V 减小到600 V 经过切换点，两种切换都能平滑稳定切换。

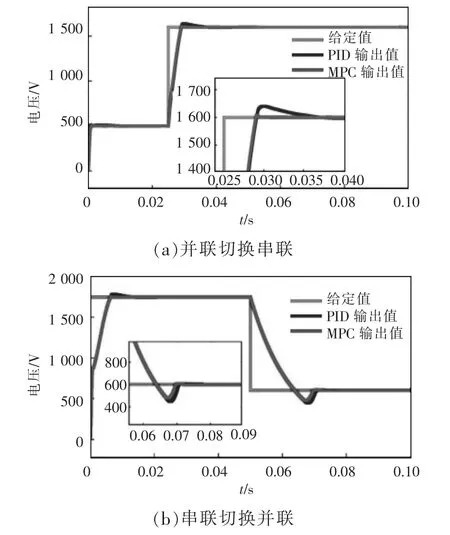
图15 串联和并联切换电压对比Fig.15 Comparison of switching voltage between series and parallel modes

图16 为并联PWM 模式MPC 双闭环控制输出电压波形，可知在并联PWM 模式下MPC 双闭环控制可实现电压稳定跟随。

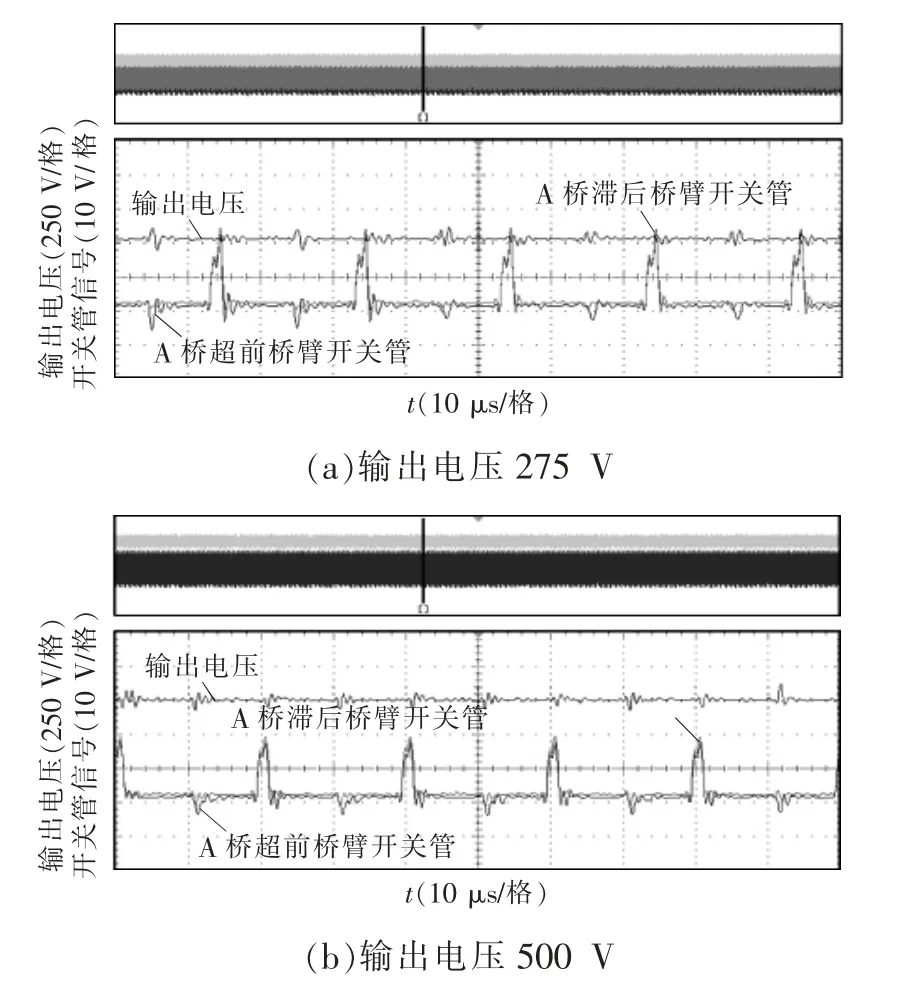
图16 并联PWM 模式MPC 双闭环控制输出电压Fig.16 Output voltage under MPC dual closed-loop control in parallel PWM mode

4 结论

（1）新型双全桥拓扑采用两个变压器原边并联、副边串联或并联的结构，可满足屏栅电源宽范围电压输入条件下宽范围电压输出的要求。

（2）基于屏栅电源新型双全桥拓扑，提出的模型预测双闭环控制算法，不仅有效解决了由负载和未知电感等引起的模型失配问题，而且提高了系统的动态性能、稳态性能。

（3）与经典PID 控制相比，模型预测控制在给定突加或突减、负载突加或突减时，能更快地恢复到给定值，有效提高了系统的抗扰动性能。