磁集成开关电容高增益级联Boost 变换器

荣德生，陈 靓，任 杰，朱晓林

（1.辽宁工程技术大学电气与控制工程学院，葫芦岛 125105；2.国网内蒙古东部电力有限公司通辽供电公司，通辽 028000；3.国网奈曼旗供电公司，奈曼旗 028300）

传统的非绿色廉价能源已经无法负担当今世界对能源服务的需求以及维持可持续生态系统的要求，光伏发电则是将清洁太阳能源转换为电能的一项操作难度较小、可控制成本与规模的有效手段[1-2]。在实际应用中，为实现顺利并网、或达到并网系下级交流负载的对应供能要求、或作为蓄电池的充电组件，在优化设计并网逆变器时，传统的低压直流电源无法直接提供给交直流负载，更加不适于微电网或并网系统发电，除输入端直接采用多电池的光伏矩阵，还需要进一步利用变换器提升电压增益。现阶段为最终满足发电系统的电能质量，研究高增益、高效率、低纹波性能优秀的变换器具有极其重要的意义。

传统Boost 变换器及其他基本DC-DC 变换器虽具有升压能力，但升压能力不足[2]。为了提升DCDC 变换器的电压增益，文献[3]将开关电感引入Cuk变换器中，通过开关电感结构中的两电感并联储能，串联放电，实现了提升Cuk 变换器的电压增益；文献[4]通过将开关电感与有源开关电感相结合，提出了一种有源开关电感网络，进一步提升了变换器的电压增益；文献[5]具体总结了开关电感在各个变换器中的应用，开关电感虽可提升变换器电压增益，但其并不能减小开关管的电压应力；文献[6]利用电压升举技术，通过自举电容倍压方式，在提升变换器的电压增益的同时减小了开关管的电压应力；文献[7-9]具体分析了基本级联Boost 变换器（又称二次型Boost 变换器）的工作原理；文献[10]将文献[6]所提自举电容引入单管级联Boost 变换器，提升变换器的电压增益。上述文献虽提出各种拓扑结构，但并未考虑变换器中的磁性元器件集成以及电流纹波减小问题。文献[11]将磁集成技术引入Buck-Boost 变换器中，通过电感集成的方式，减小了电感电流纹波，提升了变换器的功率密度。

本文在文献[7-11]的基础上，为了提升基本级联Boost 变换器的电压增益，通过组合开关电容DCM（diode capacitor multiplier）单元，同时对级联变换器中的两电感进行磁集成，提出一种新型的磁集成开关电容高增益级联变换器。变换器在进一步提高电压增益的同时，有效减小了开关管的电压应力。由于变换器输入端存在电感，通过磁集成设计，设置合理的电感集成参数，实现了变换器的低输入纹波。

1 变换器的拓扑结构及工作原理

1.1 拓扑结构

基本级联Boost 变换器又称二次型Boost 变换器，所谓二次即变换器可实现与占空比呈平方关系的电压增益，变换器拓扑结构如图1 所示。然而基本级联变换器相比Boost 变换器虽增益明显提升，但开关管以及输出二级管的电压应力依旧等于输出电压。为了改善上述问题，引入开关电容结构，将开关电容中的两个DCM 倍压单元拆开，将其与级联Boost 变换器前级储能结构进行组合，如图2（a）所示，电容C1可视作一个电压源，两端分别连接一个DCM 单元，电容C1与DCM 单元中的电容C2、C3均起到倍压的作用。再将变换器中的两电感进行磁集成，得到磁集成开关电容高增益级联Boost 变换器，如图2（b）所示，通过设计合理的耦合系数，减小电感电流纹波大小，提升变换器的功率密度。

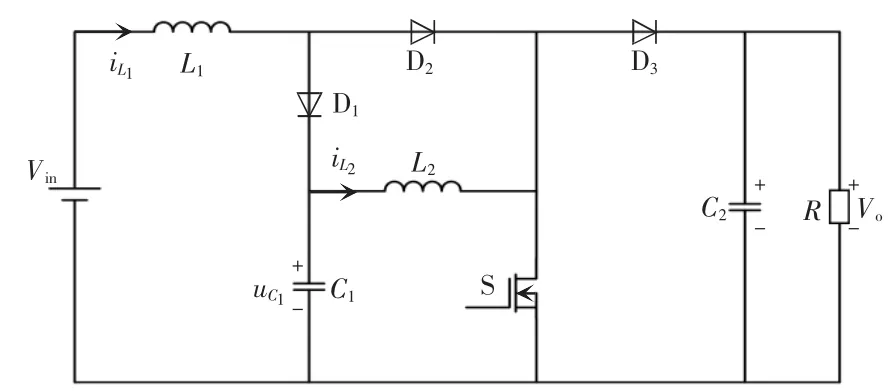
图1 基本级联Boost 变换器拓扑结构Fig.1 Topology structure of basic cascaded Boost converter

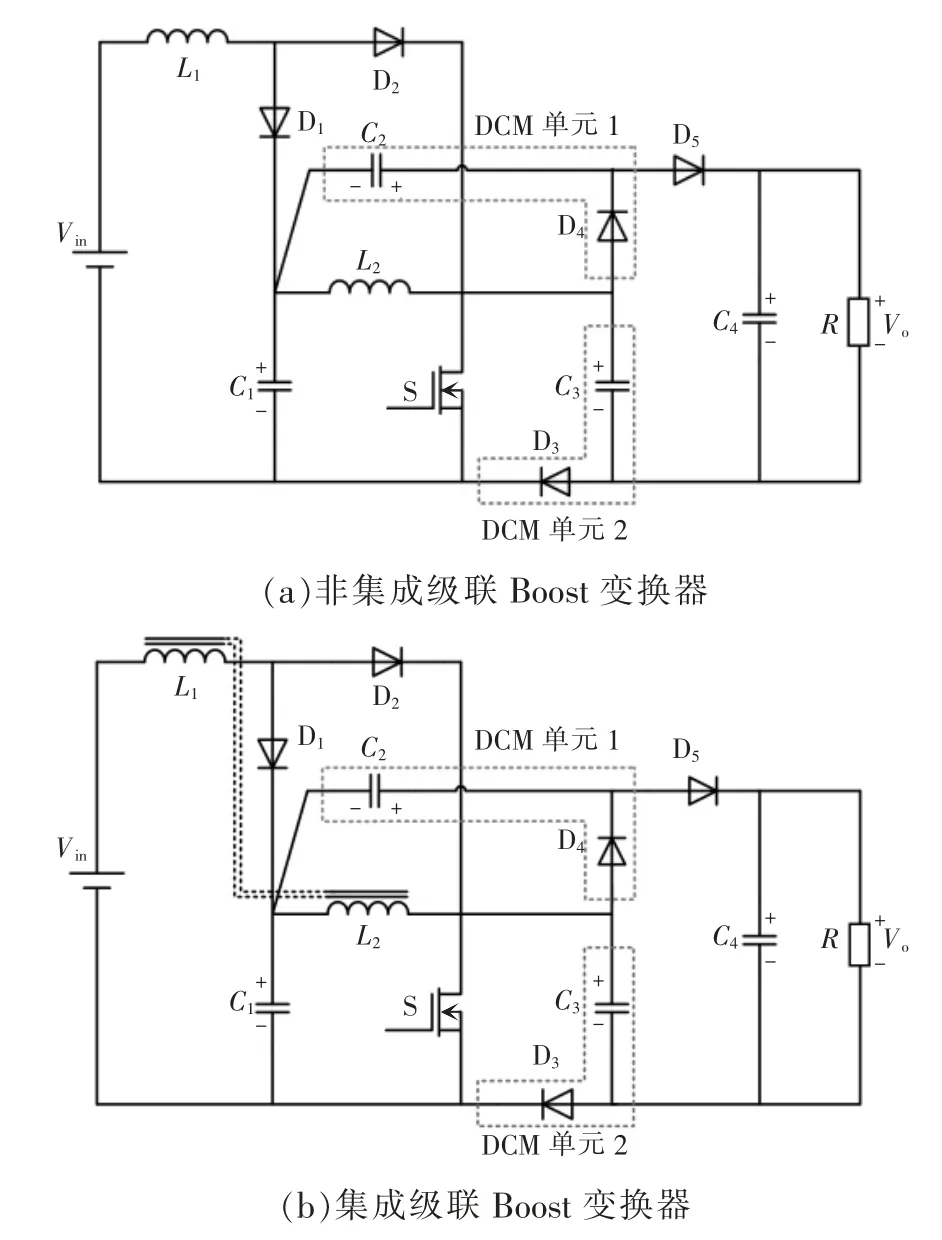
图2 开关电容高增益级联Boost 变换器Fig.2 Switch capacitor high-gain cascaded Boost converter

1.2 变换器工作模态

为了便于分析变换器的工作原理，首先做出以下假设：①涉及的开关管和二极管都是理想器件，即导通时间和关断时间均为0，关断电阻无限大，导通电压降低至0；②电感和电容均为理想器件，忽略其寄生效应；③所使用电容足够大，忽略其纹波电压。

一个工作周期内，共3 个工作模态，设占空比为D，主要工作波形如图3 所示，变换器的模态等效电路如图4 所示。

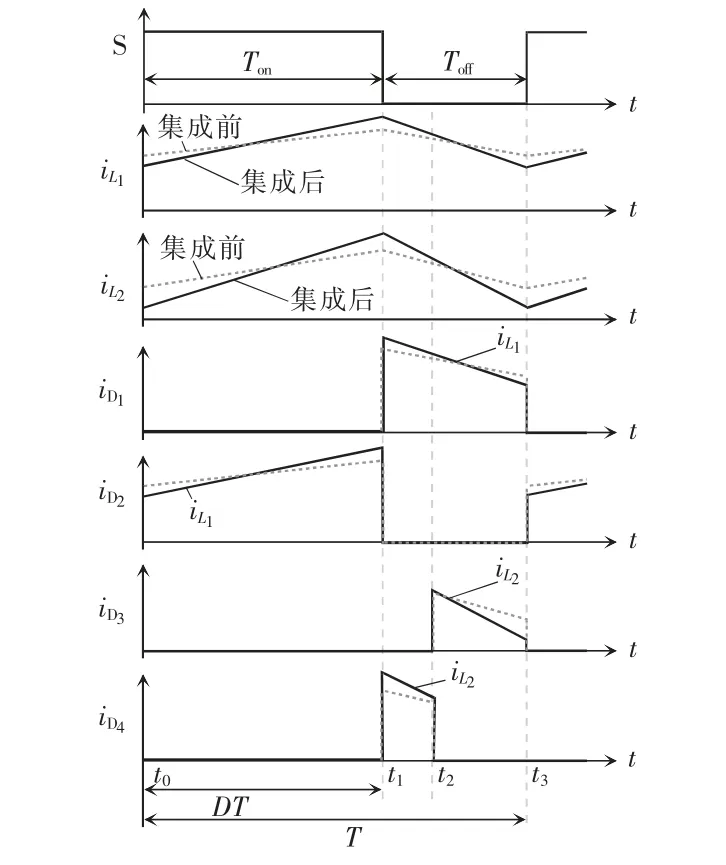
图3 变换器的主要工作波形Fig.3 Main working waveforms of converter

模态Ⅰ[t0～t1]：如图4（a）所示，开关管S 在t0时刻导通，其中二极管D2、D5导通，二极管D1、D3、D4截止，输入电源Vin通过二极管D2和开关管S 给电感L1储能，此时电感电流iL1线性增加；电容C1通过开关管S 给电感L2储能，电感电流iL2线性增加；同时电容C1与电容C2、C3串联共同为负载供电。回路表达式为

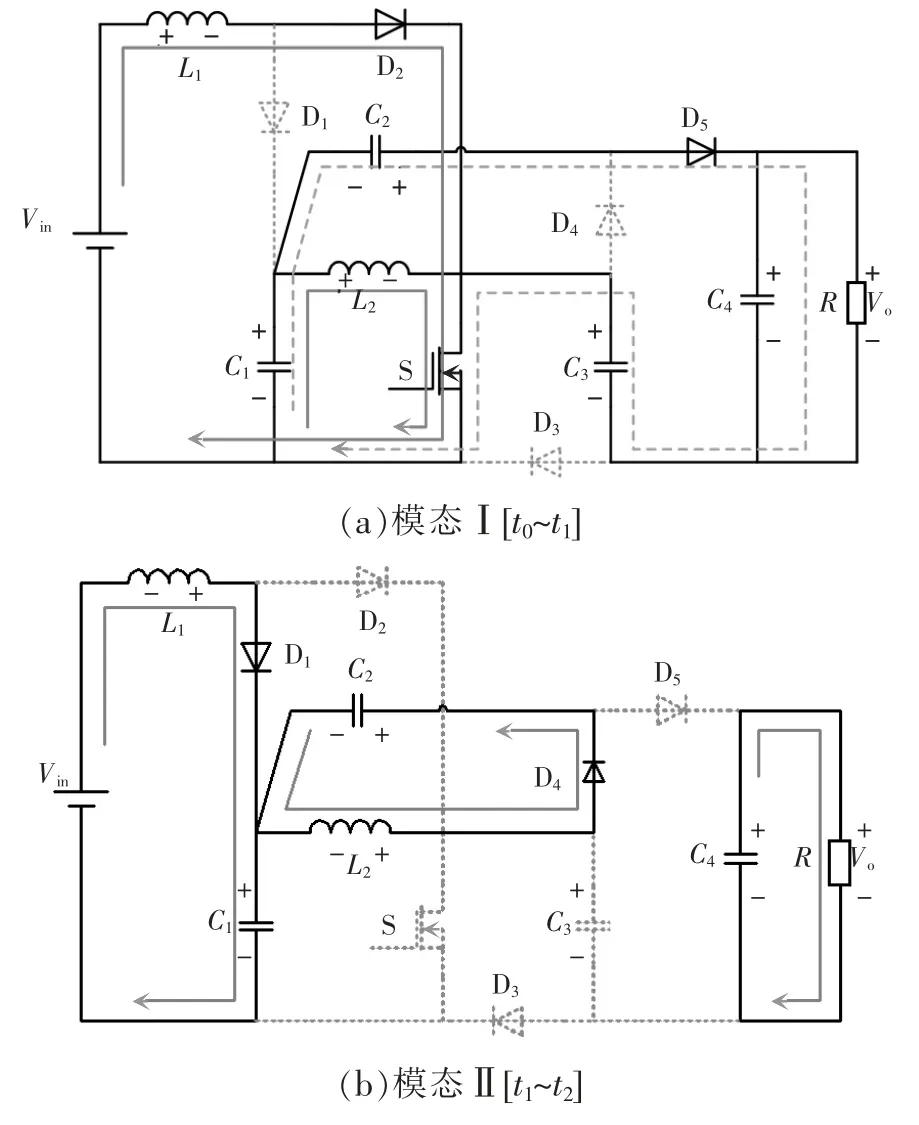
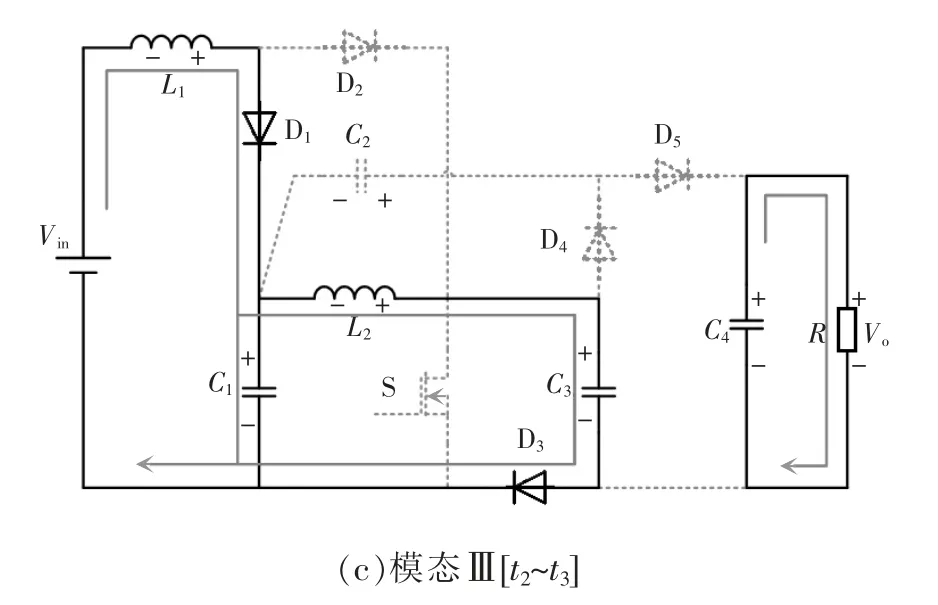
图4 不同开关模态的等效电路Fig.4 Equivalent circuits in different switching modes

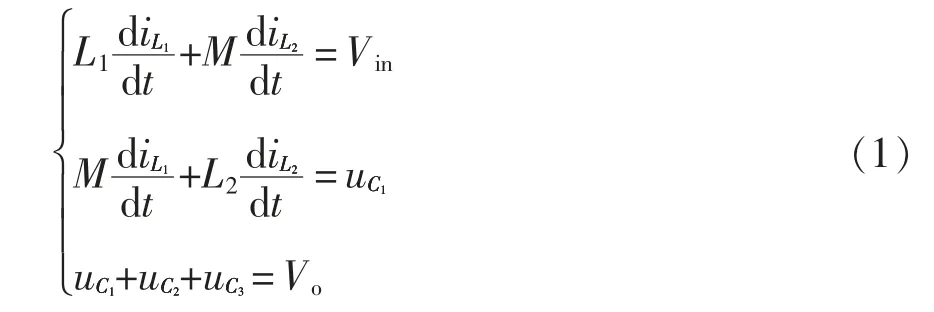
模态Ⅱ[t1～t2]：如图4（b）所示，t1时刻开关管S关断，二极管D1、D4导通，相反二极管D2、D3、D5截止；电感L1与Vin经二极管D1给电容C1充电，即电感电流iL1线性减小；电感L2通过二极管D4给电容C2充电，电感电流iL2呈线性减小；另外电容C4为负载R 供电。回路表达式为

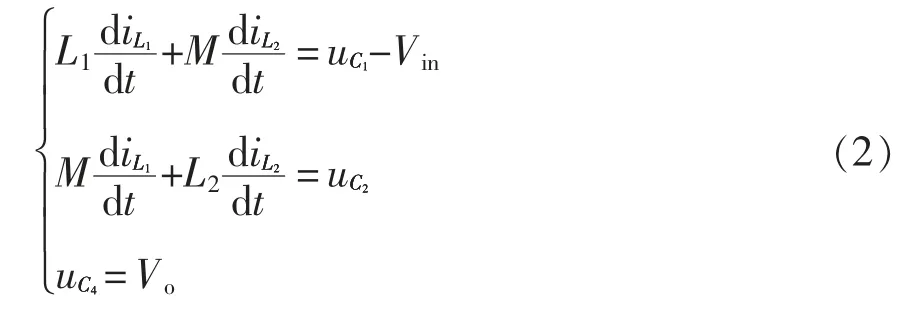
模态Ⅲ[t2～t3]：如图4（c）所示，此时开关管S，二极管D2、D5仍处关断状态，上阶段中电容C2充电电压提升，继而二级管D4在t2时刻截止，二极管D3导通，经过二极管D1、电感L1与Vin为电容C1充电，电感电流线性减小；同时，电感L1、L2通过二极管D3给电容C3充电，电感电流线性减小；电容C4为负载R 供电。回路表达式为

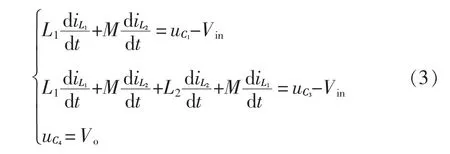
2 变换器的性能分析

2.1 变换器电压增益

经过上述分析，可发现后两个工作模态中电感L1、L2均处于放电状态，且L1、L2的电流呈相同的线性升降趋势，变化率也一致，即变换器的工作特性并没有产生实质的变化，因此分析时，模态Ⅱ和模态Ⅲ被看成相同的模态。由式（1）～式（3）得到增加的电感电流变化量为

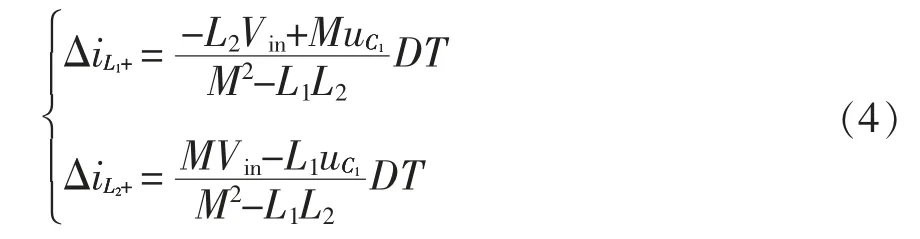
同理得到电感减小的电流变化量为

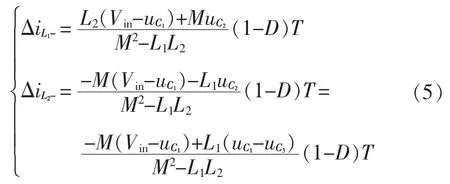
根据电感电流伏秒平衡原理，等式左右增加量等于减少量，由式（3）～式（5）可得

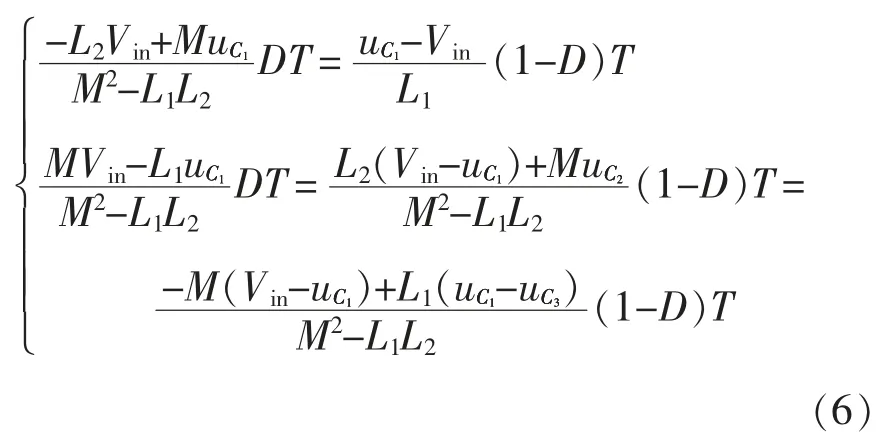
结合式（6）和式（1）可知变换器的电压增益为

由式（7）可知，通过增加两个DCM 单元，变换器的电压增益增加到基本级联Boost 变换器增益的2 倍，电压增益得到更大幅度提升。

2.2 变换器电压应力

电压应力是选择变换器功率器件的一项重要依据，由式（6）可得到各电容的电压应力为

开关管S 的电压应力为

各个二极管的电压应力分别为

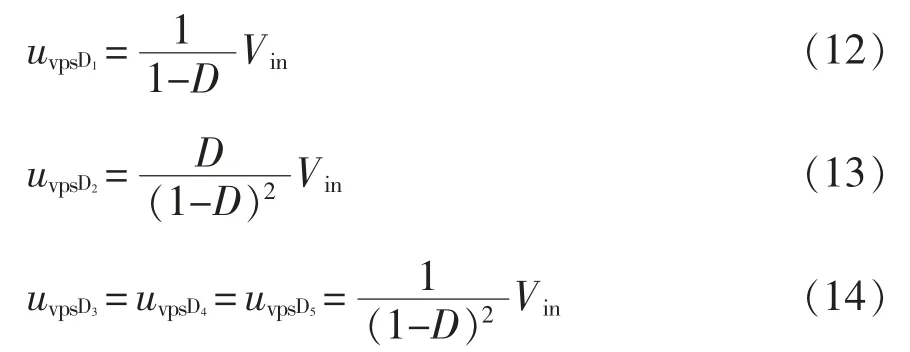
2.3 电感电流纹波与耦合度设计准则

2.3.1 电感电流纹波

输入端电压稳定，电感L1与L2产生的电流纹波不仅同自感量相关，还受互感影响[12]。假设电感L1与L2的耦合系数为k，电感L1与L2的匝数比为N，可得

将式（15）、式（16）代入式（4），同时参考各电容电压，处于电感电流上升阶段时满足

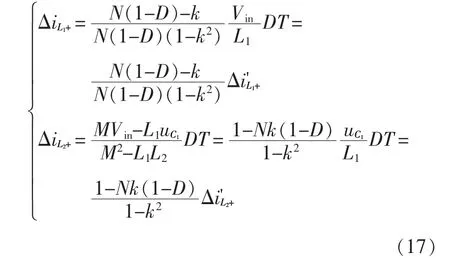
由式（17）可知，L1与L2电感的电流纹波大小与自身电感大小有关，同时受到耦合系数k 与占空比D 影响，令

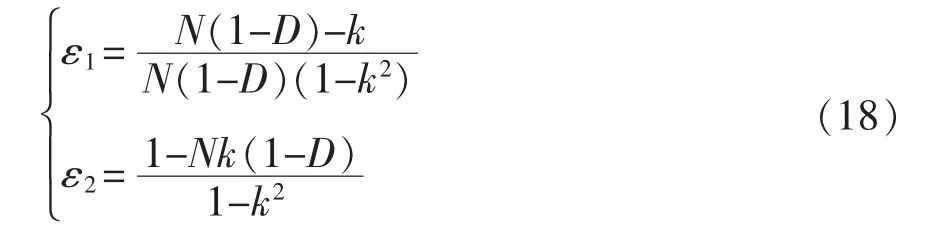
式中：ε1与ε2为电感电流L1与L2的纹波减小系数，ε1与ε2取值区间为0～1。由式（18）可得，若要电流纹波减小系数ε1=ε2，此时匝比N 与占空比D 需满足

采用占空比D 分别取0.4、0.5、0.6 为例，对应ε1、ε2和匝比N 与耦合系数k 的关系如图5 所示。

由图5 可知，垂直平面N=1/（1-D）上两变化曲面相交，式（19）的关系成立，ε1与ε2变化趋势相同。以这一平面为界，当N>1/（1-D），ε2迅速减小直至0，而ε1则先下降后又回升，适当调节匝比和耦合系数k，使两电流纹波均减小或电感L2的电流零纹波。N＜1/（1-D）时，下降直至减小为0 的为ε1，另外的ε2则先下降后上升，同理，可同时减小两电流纹波或让电感L1的电流达到零纹波。综合提升了变换器的功率密度。

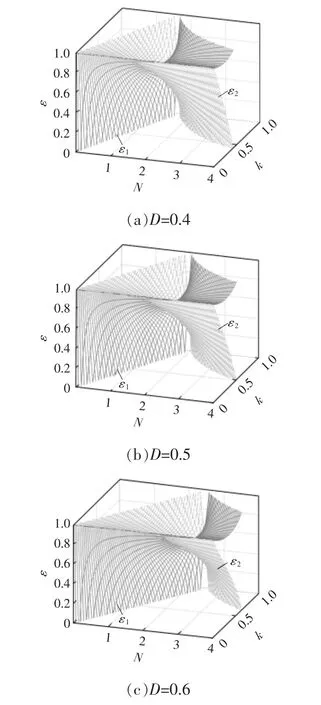
图5 ε1、ε2 和匝比N 与耦合系数k 的关系Fig.5 Relationship between ε1,ε2,turn ratio N and coupling coefficient k

2.3.2 零输入电流纹波设计准则

变换器输入端存在电感L1，其电流纹波即输入电流纹波。输入电流纹波会在一定程度上对电源或上级变换器产生电磁干扰，影响电源发电效率、降低使用寿命。据第2.3.1 节分析，将电感L1电流纹波降为0，即可实现变换器零输入纹波设计[13]。

根据式（18），令ε1=0，可得

此时对应的耦合系数k 和占空比D 与匝比N 的关系如图6 所示。将式（20）代入式（18）得到ε1=1，即当电感L1的电流纹波减小为0 的情况下，电感L2的电流纹波保持不变。

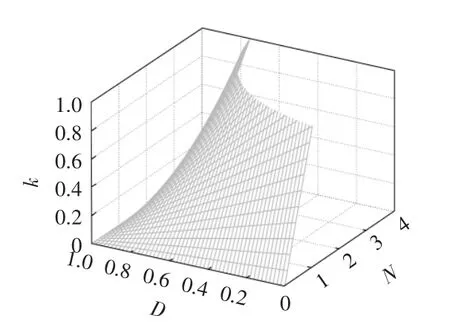
图6 耦合系数k 和占空比D 与匝比N 的关系Fig.6 Relationship of coupling coefficient k,duty ratio D and turn ratio N

2.4 变换器性能对比

基于上述理论分析，将本文变换器与其基本级联Boost 变换器以及文献[5]中提高增益级联Boost变换器进行对比，结果见表1。可知较基本级联Boost 变换器，本文所提变换器的电压增益有明显提升；较文献[5]所提改进级联变换器的电压，本文所提变换器具有更高的电压增益；对比开关管电压应力，本文所提变换器的电压应力仅为输出电压的1/2，具有更低的电压应力。

表1 不同变换器的性能对比Tab.1 Comparison of performance among different converters

3 变换器磁件设计

基于以上分析，L1、L2需进行正向耦合，耦合系数为k。考虑“EI”型磁芯[14]的结构紧凑、体积较小、具有较高工作频率、工作电压范围广、气隙在线圈顶端耦合紧、损耗低，采用左右对称型结构，具体结构和缠绕方式如图7 所示，其基本模型如图8 所示。

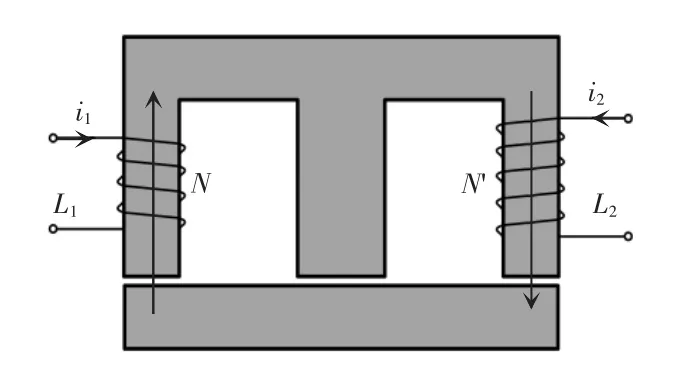
图7 “EI”型集成磁件缠绕方式Fig.7 Winding pattern of EI-type integrated magnetic component

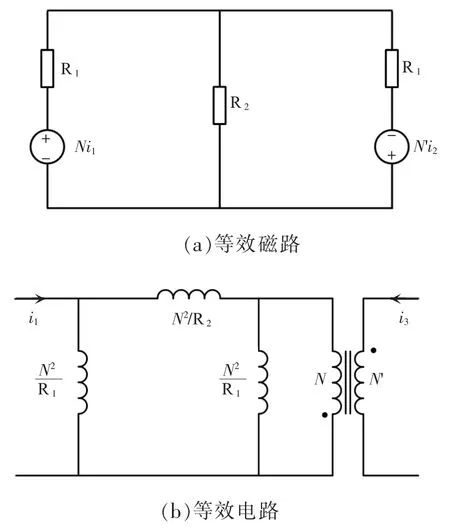
图8 “EI”型集成磁件基本模型Fig.8 Basic model of EI-type integrated magnetic component

磁件的等效磁路如图8（a）所示，R1、R2为磁柱磁阻，设电感L1的匝数为N，电感L2的匝数为N'。利用对偶尺度变换，经过一系列的等效简化，即可得到磁件的等效电路如图8（b）所示。计算电感和磁阻之间的关系，得到电感L1、L2的自感与对应两磁阻的关系为

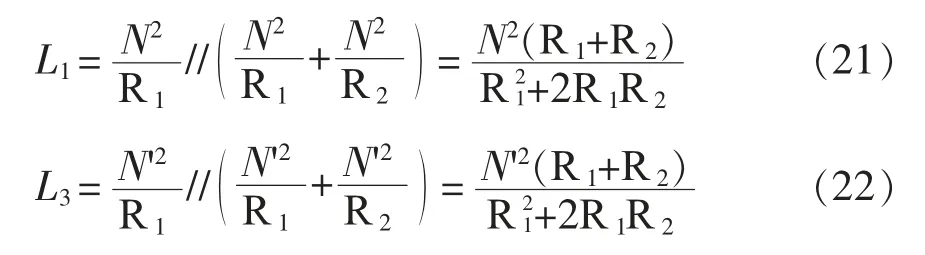
电感L1、L2之间的互感M 与相应磁阻的关系为

根据耦合系数公式，求得电感L1、L2的耦合系数k 为

4 仿真与实验验证

4.1 仿真验证

利用软件PSIM 进行仿真验证，输入电压Vin=12 V，开关管频率f=100 kHz，变换器功率100 W。占空比D=0.55、电感L1=20 μH，电感L2=80 μH、C1=C2=C3=50 μF，电容C4=100 μF，输出端负载R=120 Ω。

输出仿真结果如图9 所示。输出电压Vo的仿真波形如图9（a）所示，观察参数，变换器输出电压近似120 V，仿真结果与理论计算值相符。图9（b）中开关管S 的电压应力约为输出电压Vo的1/2，约60 V，符合理论预计情况。

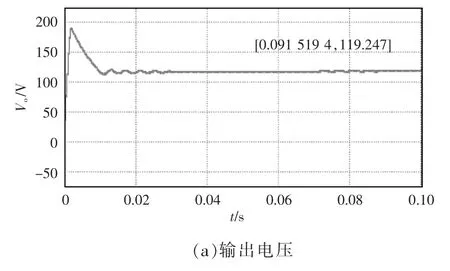
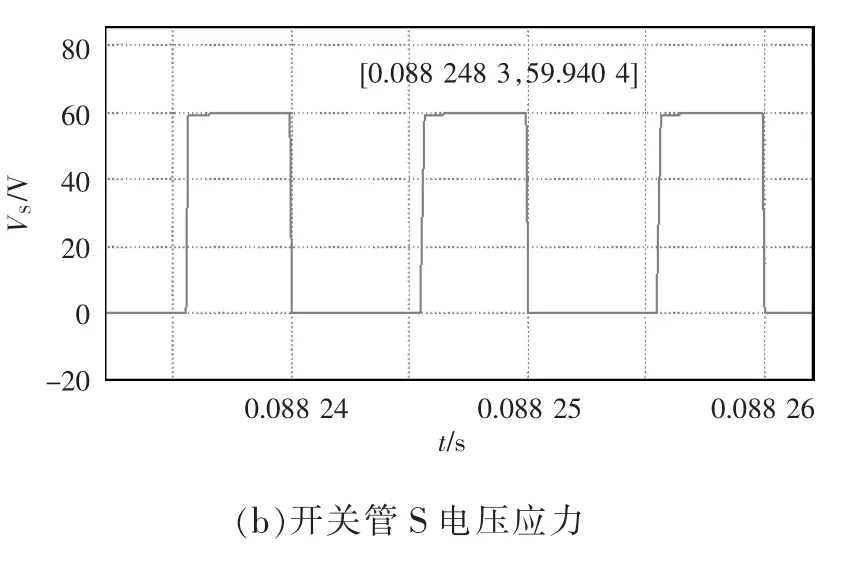
图9 输出仿真波形Fig.9 Output simulation waveforms

为实现零输入纹波，占空比D=0.55，N=2，将其代入式（20），得到k=0.9。图10 为集成前后电感L1、L2的电流纹波。横向对比，电感L1的电流纹波减小至基本为0，电感L2的电流纹波前后保持一致，符合理论。

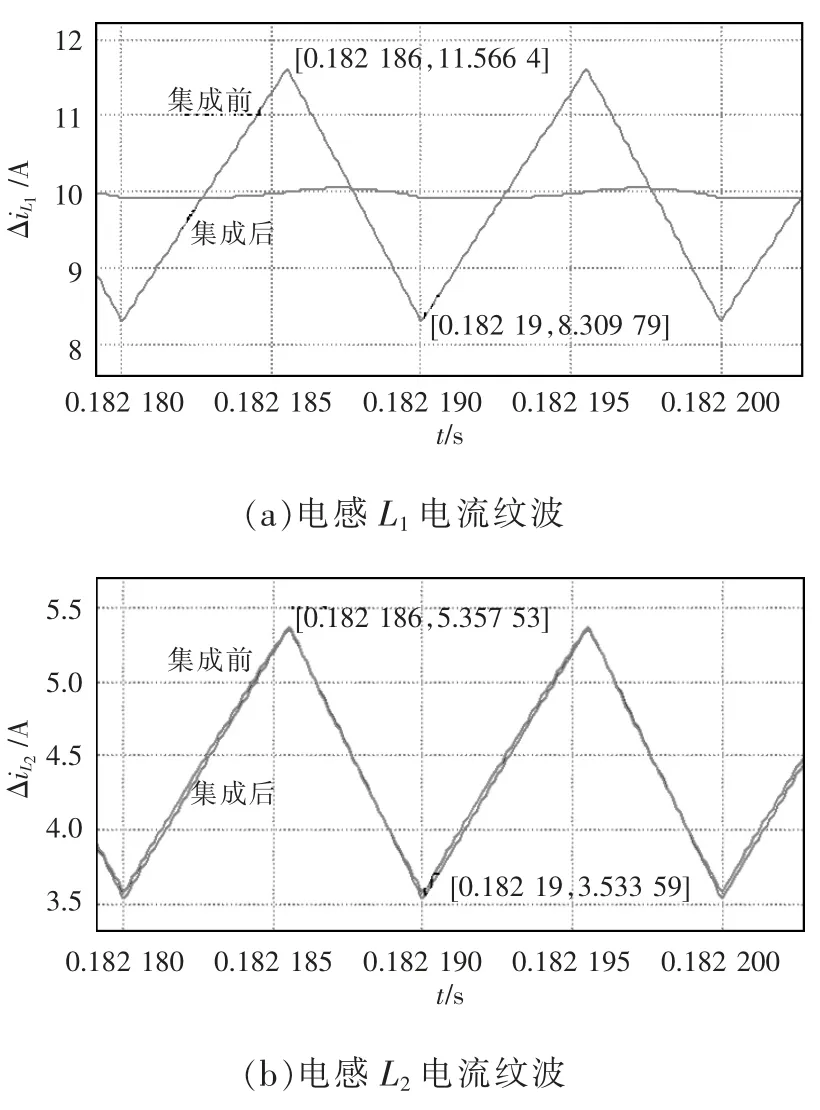
图10 电感电流纹波仿真波形Fig.10 Simulation waveforms of inductance current ripple

4.2 实验验证

设计变换器原理样机，参数同仿真参数。电感L1、L2采用“EI”型磁芯进行集成，具体电感实测值见表2。变换器主要波形如图11 所示。根据图11（a）的输出电压波形，输出电压大致为理论值120 V，增益有较高水平。图11（b）开关管电压应力波形，数值在60 V 左右，仅为输出电压的1/2，应力较小。

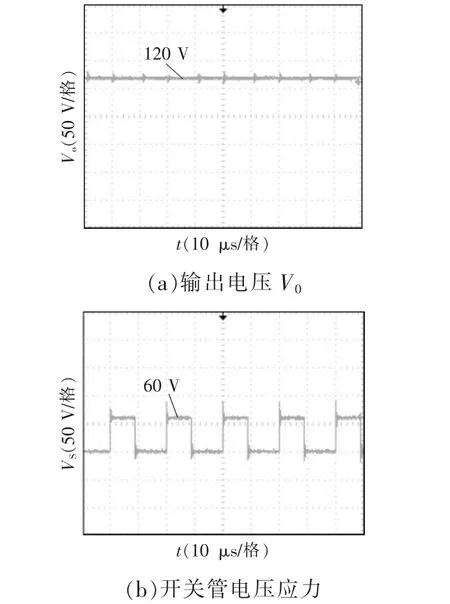
图11 变换器主要波形Fig.11 Main waveforms of converter

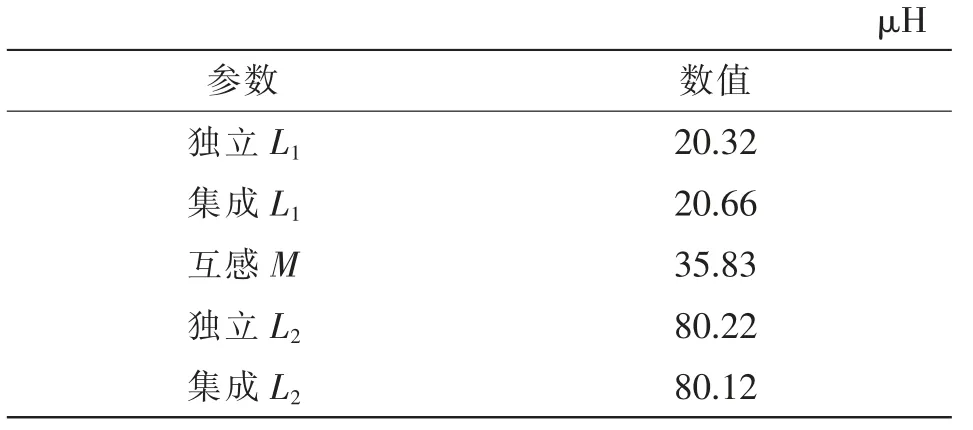
表2 电感实测值Tab.2 Measurement values of inductance

L1、L2集成前后对应的电流纹波如图12 所示，电感L1的电流纹波明显减小，纹波大小基本在0上下浮动，基本实现了输入零纹波要求，另外的电感L2电流纹波基本保持不变，稳定在1.8 A，符合设计要求和理论分析。

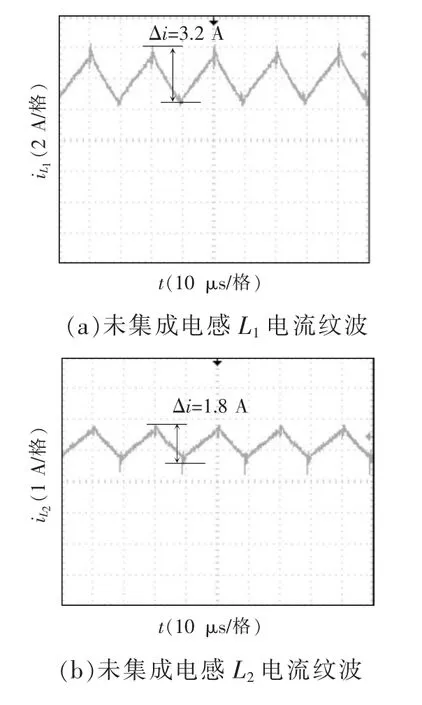
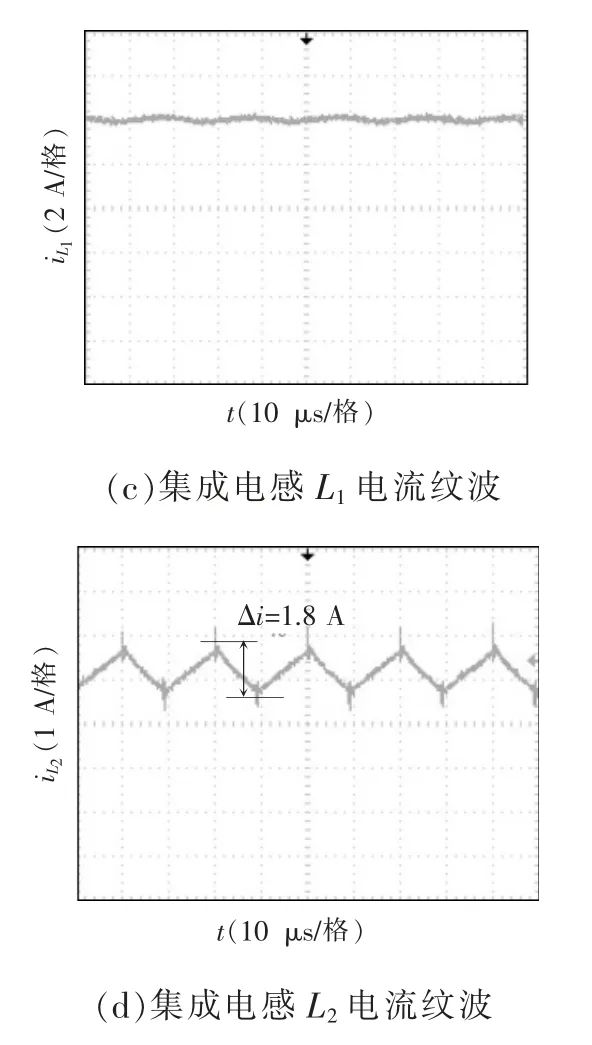
图12 集成前后电感电流纹波Fig.12 Inductance current ripple before and after integration

5 结论

本文在基本级联Boost 变换器的基础上，通过引入DCM 倍压单元以及磁集成技术，提出一种磁集成开关电容高增益级联Boost 变换器，理论分析和实验结果表明该变换器与传统的级联Boost 变换器对比具有以下特点：

（1）针对电压增益在级联Boost 变换器的提升情况下再次增长了一倍，为传统Boost 变换器电压增益的2/（1-D）倍。

（2）开关管的电压应力仅为对应输出电压的1/2，减小电流纹波的同时降低了器件的成本。

（3）应用磁集成技术，给出了适用于此变换器的磁集成设计准则，并通过设计合理的耦合系数k，实现了变换器输入电流零纹波，提升了变换器的性能。