带有时滞和非线性收获效应的分数阶捕食者-食饵模型的Hopf 分岔
王鑫梅,张道祥
(安徽师范大学数学与统计学院,安徽 芜湖 241002)
可再生资源(如渔业、林业资源等)会因过度开采受到损害而衰退,所以近几十年来,对可再生资源的理论评估有了迅速发展[1-2].现有研究结果表明收获效应对捕食者-食饵系统动力学有着重要影响,其中收获率包括常数收获率[3-4]、线性收获率[5-6]和非线性收获率[7-8].刘霞等[7]研究了一类具有非线性收获的捕食系统的分支特性,发现系统的动力学性质由于非线性收获的出现变得更加复杂.Sambath等[9]研究了捕食者具有双曲死亡率的捕食者-食饵模型的Hopf分支方向以及产生周期解的稳定性:

(1)


(2)
其中正常数h代表非线性收获效应项的收获系数.
事实上,生物种群密度的变化受到诸如妊娠等时滞因素的影响.所以时滞微分方程模型被广泛研究[11-12].另外,分数阶微积分是整数阶微积分的一般情况,由其建立的模型能够更准确地描述系统的动态行为[13-14].基于以上考虑,本文将研究如下一类具有时滞和非线性收获效应的分数阶捕食者-食饵模型:
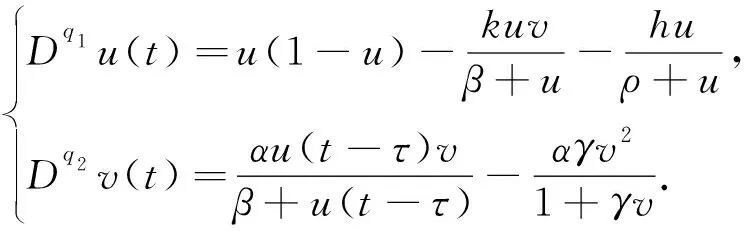
(3)

本文主要讨论系统(3)的Hopf分岔特性.与文献[9-10]不考虑时滞和分数阶指数不同,本文系统地讨论了时滞效应、分数阶指数、非线性收获效应对捕食系统稳定性的影响,因此所提出的模型更加真实且具有更丰富的动力学特性.下文先给出系统(3)正平衡点的存在定理以及局部稳定性和Hopf分岔定理,然后通过数值模拟分析时滞、非线性收获效应及分数阶指数对Hopf分岔的影响,最后得出结论.
1 局部稳定性和Hopf分岔
为了获得生物学平衡点,首先考虑如下方程:
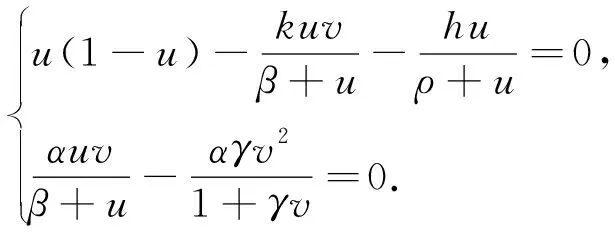
(4)
并作出假设(H1)ρ>h.
定理1当条件H1成立时,方程(4)至少存在一个正平衡点X*(u*,v*).
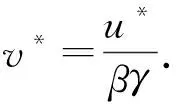
A0u3+A1u2+A2u+A3=0.
(5)

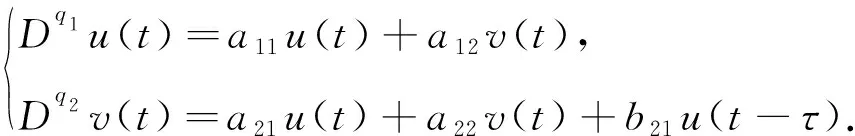
(6)

考虑系统(3)在正平衡点X*(u*,v*)的局部稳定性,即考虑线性化系统在(0,0)处的稳定性,对线性化系统的两端进行Laplace变换:

(7)
M1(s)+M2(s)e-sτ=0.
(8)
其中,M1(s)=sq1+q2-a22sq1-a11sq2+a11a22,M2(s)=-a12b21.
首先,考虑当τ=0时,系统(3)在正平衡点X*(u*,v*)处的稳定性.假设(H2)a11≤0.
定理2当τ=0和假设H2成立时,系统(3)的正平衡点X*(u*,v*)是局部渐近稳定的.
证明当τ=0时,由特征方程(8)可得
λ2+B1λ+B2=0.
(9)
其中,B1=-(a11+a22),B2=a11a22-a12b21.注意到a12<0,a22<0,b21>0和条件H2成立,可得B1>0,B2>0.由Routh-Hurwitz定理可知,方程(9)的根都有负实部.基于分数阶微分方程稳定性的判据[15],当τ=0时,系统(3)在正平衡点X*(u*,v*)处是局部渐近稳定的.
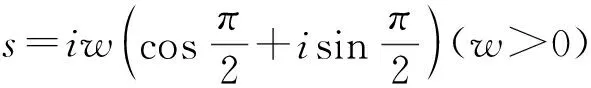

(10)
其中,
对式(10)求解,有

(11)
又cos2wτ+sin2wτ=1,可以得到关于w的方程:
g12(w)+g22(w)=1.
(12)
为了得到本文的主要结果,假设式(12)至少有一个正实根w0.再根据方程(11)中的第一个式子,可得
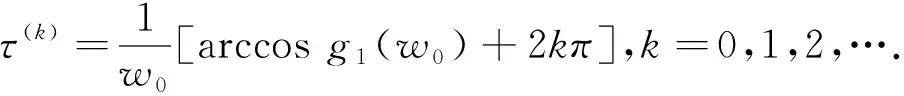
(13)
进一步定义分岔点τ0=min{τ(k)},k=0,1,2,….


证明对特征方程(8)的两边关于τ求导:
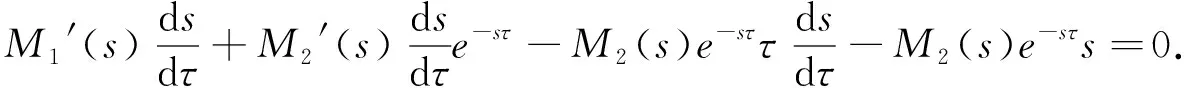
(14)
化简可得

(15)
因此当假设H3成立时,
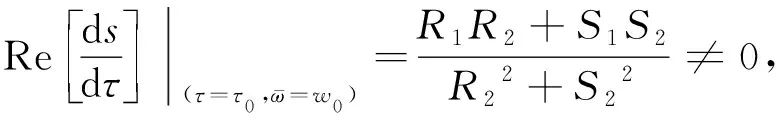
(16)
即横截性条件成立.基于以上讨论,可以推导出如下定理:
定理4假设条件H1—H3成立,那么对于系统(3):
ⅰ)当τ∈[0,τ0)时,正平衡点X*(u*,v*)是局部渐近稳定的;
ⅱ)当τ=τ0时,在正平衡点X*(u*,v*)附近发生Hopf分岔,产生周期解.
2 数值模拟
选择参数β=0.48,ρ=0.2,γ=1,k=0.6,h=0.12,α=1.35,q1=0.95,q2=0.95进行数值模拟.
2.1 时滞对系统的影响
通过计算可得系统(3)的正平衡点为X*(0.286 2,0.596 4),时滞临界值τ0=2.655 1.并且容易验证选取的参数值满足条件H1—H3,从而根据定理4,若τ=2<τ0,那么系统(3)的正平衡点X*是局部渐近稳定的(图1),当时间t>250时,u(t)、v(t)分别稳定在0.286 2和0.596 4;若τ=2.7>τ0,那么系统(3)在正平衡点X*附近发生Hopf分岔产生周期解(图2).

图1 q1=0.95, q2=0.95, τ=2<τ0时系统(3)的状态轨线和相图Fig.1 State trajectories and phase diagram of system (3) with q1=0.95, q2=0.95, τ=2<τ0图2 q1=0.95, q2=0.95, τ=2.7>τ0时系统(3)的状态轨线和相图Fig.2 State trajectories and phase diagram of system (3) with q1=0.95, q2=0.95, τ=2.7>τ0
当q1=q2=1时,系统(3)即为常微分系统,计算得到常微分系统的临界时滞τ0*=2.064 4,由定理4知,当τ∈[0,2.064 4)时系统平衡点达到稳定,而上述分数阶系统当τ∈[0,2.655 1)时平衡点达到稳定.不难发现,当系统为分数阶时,系统的Hopf分岔延迟发生,同时系统的稳定性区域扩大.
2.2 收获效应对系统的影响
考虑收获效应h对系统(3)正平衡点稳定性的影响.h在区间[0,0.15]上取不同的值,可以得到一系列的正平衡点X*(u*,v*).从图3中可以看出,随着收获效应h的增加,捕食者和被捕食者的数量都在减少.这说明随着对食饵的捕捞,捕食者的食物会减少,从而导致捕食者数量减少.根据对式(12)和(13)的计算,可以得到τ0和收获效应h的关系图,如图4所示,τ0随着h的增加而减小,且曲线将平面分成上下两个区域,曲线的上方为不稳定区域,曲线的下方为稳定区域.

图3 h与正平衡点X*的关系Fig.3 The relation between h and X*图4 τ0与收获效应h的关系Fig.4 The relation between τ0 and h
根据以上分析,在稳定区域取τ0=2.85和h=0.02.图5表示系统(3)在此参数条件下的积分曲线,可见系统(3)在正平衡点X*(u*,v*)处是局部渐近稳定的.在不稳定区域取τ0=2.85和h=0.1,图6表明系统(3)在正平衡点X*(u*,v*)附近出现Hopf分岔并产生了极限环.

图5 τ=2.85和h=0.02的积分曲线Fig.5 The integral curve of τ=2.85 and h=0.02图6 τ=2.85和h=0.1的积分曲线Fig.6 The integral curve of τ=2.85 and h=0.1
2.3 分数阶指数对系统的影响
考虑分数阶指数对系统(3)稳定性的影响.固定q2=0.95,利用Matlab计算得到q1与τ0的关系(图7),随着q1的增大,τ0逐渐减小,即Hopf分岔会提前发生.这个结果也可以从图8中得到验证.
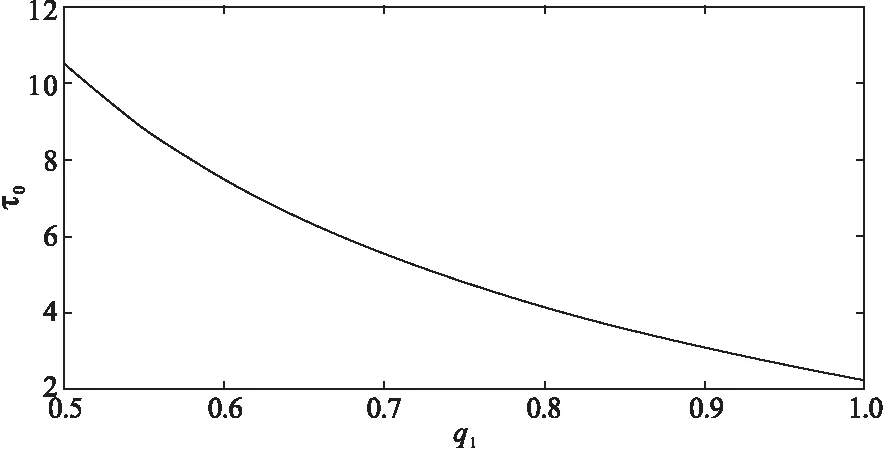
图7 系统(3)的分数阶指数q1与τ0的关系Fig.7 The relation between q1 and τ0 of system (3)
图8所示为q1=0.7,0.8,0.9和τ=2.5,q2=0.95时,系统(3)在正平衡点X*处关于u和v的状态轨线和相图.可以看出,q1越小,对系统(3)振荡的抑制效果越明显,系统(3)在正平衡点X*处会更早地趋于稳定.



图8 q2=0.95, τ=2.5, q1=0.7,0.8,0.9时系统(3)的状态轨线和相图Fig.8 State trajectories and phase diagram of system (3) with q2=0.95, τ=2.5, q1=0.7,0.8,0.9
注1q1、q2其中一个减小,会抑制分数阶系统的振荡行为,从而使得系统提前稳定.这与文献[15]的结果一致.
3 结 论
本文首先建立了带有时滞和非线性收获效应的分数阶生态动力学模型,并分别研究了时滞、收获效应和分数阶指数对模型Hopf分岔的影响.理论结果表明,当时滞达到某个确定的临界值时,系统在正平衡点会产生Hopf分岔从而出现周期解.数值结果表明,收获效应会影响系统平衡点的稳定性;分数阶指数也能改变系统平衡点的稳定性,分数阶指数越小,系统的正平衡点达到稳定的时间越短.

