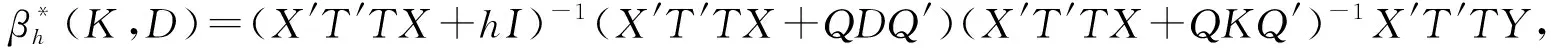聚集数据线性模型广义聚集双参数改进估计的相对效率
余新宏,朱文君,郑剑平
(合肥经济学院基础课教学部,安徽 合肥 230011)
0 引言
考虑线性模型
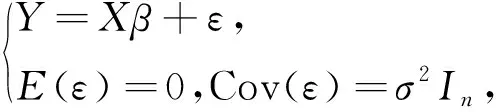
(1)
其中,Y是n×1的观测随机向量,X是n×p列满秩的设计阵,β是p×1未知参数向量,ε是n×1的未知随机误差向量,n≥p.
在线性模型的缺落值及数据挖掘、动植物研究、经济计量等问题中,一般不能完全观测到Y,而只能观测到Y的一部分分量或Y的某些线性组合,这种情况下获取的变量Y的数据称为聚集数据.通常情况下,可观测到向量Z=TY,其中T为已知n阶方阵.对此,文献[1]提出了Peter & Karsten估计:
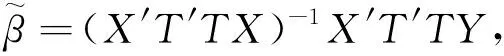
(2)
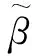
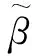
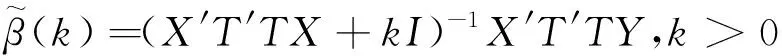
(3)
并提出了聚集数据线性模型参数的广义岭估计[4]:
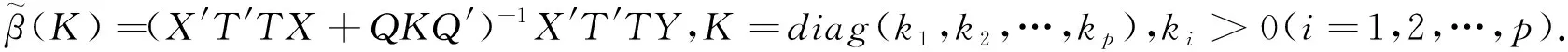
(4)
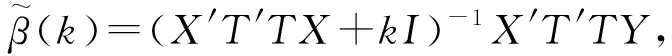
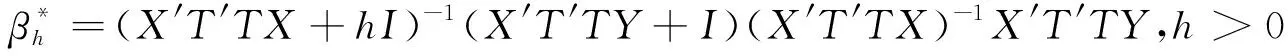
(5)
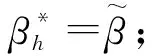
岭型估计过于重视估计参数的稳定性而轻视了其无偏性影响,常使得估计参数的均值与实际值产生较大的偏离.Liu型估计的优点在于通过引入新的参数,使得估计既能保证估计参数的稳定性,又能保证估计参数的近似无偏性,因而这方面的研究与应用为一些学者所热捧.周永正等[6]提出了聚集数据线性模型广义聚集双参数估计:
β*(K,D)=(X′T′TX+I)-1(X′T′TX+QDQ′)(X′T′TX+QKQ′)-1X′T′TY.
(6)
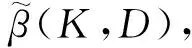
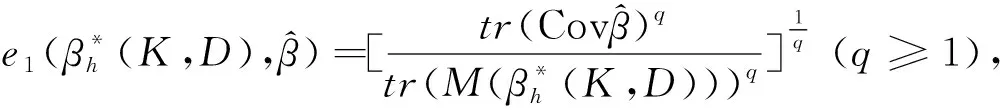
(7)
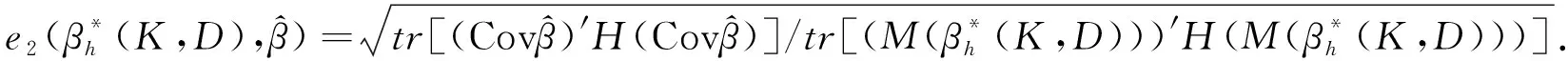
(8)
上述效率分别称为推广欧氏模之比意义下的效率和加权欧氏模之比意义下的效率.
注1本文中λi(A)表示方阵A的第i个顺序特征值.
1 定义和引理
定义1在线性模型(1)下,未知参数向量β的估计
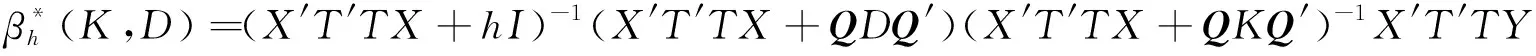
(9)
称为聚集数据线性模型参数β的广义聚集双参数改进估计.其中,D=diag(d1,d2,…,dp),K=diag(k1,k2,…,kp),0
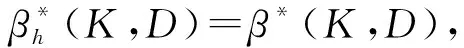
注3在定义1中,当d1=d2=…=dp=h时,得
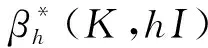
注4在定义1中,当d1=d2=…=dp=1,k1=k2=…=kp=0时,得
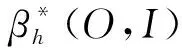
引理1设U为n×p阶矩阵.Δ=diag(δ1,δ2,…,δp),δ1≥δ2≥…≥δp>0,且U′U=Δ,则对于任意n阶矩阵A>0,有:
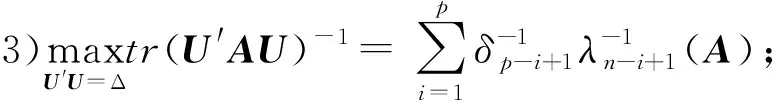
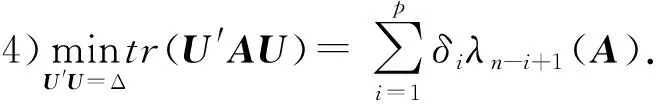
证明见文献[7].
引理2设A、B为n阶实对称矩阵,且B>0,则有
λn(B)λi(A2)≤λi(ABA)≤λ1(B)λi(A2)(i=1,2,…,n).
(10)
证明见文献[8].
引理3设A为P阶正定阵,则有p1-q(trA)q≤trAq≤(trA)q(q≥1).
证明见文献[8].
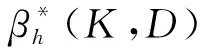
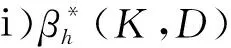
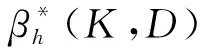
证明
(X′T′TX+hI)-1(X′T′TX+I)(X′T′TX+I)-1(X′T′TX+QDQ′)(X′T′TX+
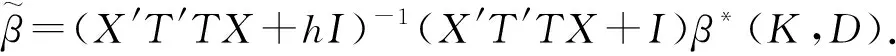
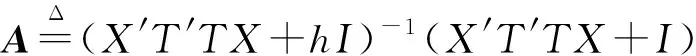
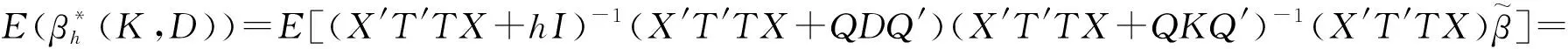
A(X′T′TX+I)-1(X′T′TX+QDQ′)(X′T′TX+QKQ′)-1(X′T′TX)β=
AB(X′T′TX)β.
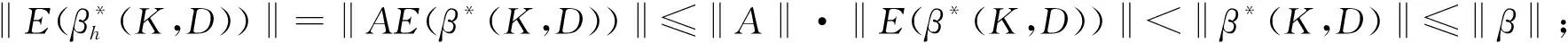
为了讨论此类有偏估计的优良性,首先需要进入下列定义.
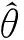
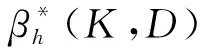
证明设q1,q2,…,qp为X′T′TX对应于特征值λ1,λ2,…,λp的标准正交特征向量,记
Q=(q1,q2,…,qp), Λ=diag(λ1,λ2,…,λp),
(ABX′T′TX-I)ββ′(ABX′T′TX-I)′ ;
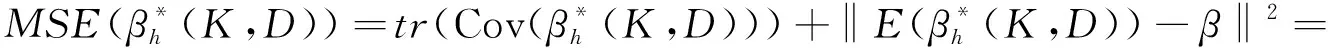
σ2ABX′T′TXB′A′+(ABX′T′TX-I)ββ′(ABX′T′TX-I)′ ;
MSE(β*(K,D))=tr(Cov(β*(K,D)))+‖E(β*(K,D))-β‖2=
σ2BX′T′TXB′+(BX′T′TX-I)ββ′(BX′T′TX-I)′.
因此,
σ2ABX′T′TXB′A′+(ABX′T′TX-I)ββ′(ABX′T′TX-I)′-
σ2BX′T′TXB′+(BX′T′TX-I)ββ′(BX′T′TX-I)′=
其中,b1=(ABX′T′TX-I)ββ′(ABX′T′TX-I)′,b2=(BX′T′TX-I)ββ′(BX′T′TX-I)′.因为
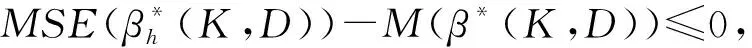
3 广义聚集双参数改进估计代替最小二乘法对的估计效率
定理2设n阶方阵T的秩为Rank(T)=p,X′X的特征值为δ1≥…≥δp>0,TT′的特征值为h1≥…≥hp>0,X′T′TX的特征值为λ1≥…≥λp>0,k1≥…≥kp≥0,0 (11) 设B=(X′X)-1,由引理3知 又设 V=TX(X′T′TX+QKQ′)-1(X′T′TX+QDQ′)(X′T′TX+hI)-1Q, 其中Q为正交矩阵,且Q′X′T′TXQ=Λ. V′V=Q′(X′T′TX+hI)-1(X′T′TX+QDQ′)(X′T′TX+QKQ′)-1X′T′TX· (X′T′TX+QKQ′)-1(X′T′TX+QDQ′)(X′T′TX+hI)-1Q= Q′(X′T′TX+hI)-1QQ(X′T′TX+QDQ′)QQ′(X′T′TX+QKQ′)-1QQ′· (X′T′TX)QQ′(X′T′TX+QKQ′)-1QQ′(X′T′TX+QDQ′)QQ′(X′T′TX+hI)-1Q= (Λ+hI)-1(Λ+D)(Λ+K)-1Λ(Λ+K)-1(Λ+D)(Λ+hI)-1= diag[(λ1+h)-2·(λ1+d1)2·(λ1+k1)-2λ1,…,(λi+h)-2·(λi+di)2·(λi+ki)-2λi,…, (λp+h)-2·(λp+dp)2·(λp+kp)-2λp]. 又由引理1、引理2可得 tr(C)=tr(Q′CQ)=tr[Q′(X′T′TX+hI)-1(X′T′TX+QDQ′)(X′T′TX+QKQ′)-1X′T′TT′TX· (X′T′TX+QKQ′)-1(X′T′TX+QDQ′)(X′T′TX+hI)-1Q]≥ 从而 故有 定理3设n阶方阵T的秩为Rank(T)=p,X′X的对应特征值为δ1≥…≥δp>0,TT′的对应特征值为h1≥…≥hp>0,X′T′TX的对应特征值为λ1≥…≥λp>0,H的对应特征值为q1≥…≥qp>0,k1≥…≥kp≥0,0 (12) 又因 σ2[(X′T′TX+hI)-1(X′T′TX+QDQ′)(X′T′TX+QKQ′)-1X′T′TT′TX· (X′T′TX+QKQ′)-1(X′T′TX+QDQ′)(X′T′TX+hI)-1+σ-2εε′], σ4tr{[(X′T′TX+hI)-1(X′T′TX+QDQ′)(X′T′TX+QKQ′)-1X′T′TT′TX· (X′T′TX+QKQ′)-1(X′T′TX+QDQ′)(X′T′TX+hI)-1+σ-2εε′]}· H·[(X′T′TX+hI)-1(X′T′TX+QDQ′)(X′T′TX+QKQ′)-1X′T′TT′TX· (X′T′TX+QKQ′)-1(X′T′TX+QDQ′)(X′T′TX+hI)-1+σ-2εε′]. 设B=(X′X)-1, C=(X′T′TX+hI)-1(X′T′TX+QDQ′)(X′T′TX+QKQ′)-1X′T′TT′TX· (X′T′TX+QKQ′)-1(X′T′TX+QDQ′)(X′T′TX+hI)-1, 设P为正交矩阵,使P·diag(q1,q2,…,qp)·P′=H. tr(BHB)=tr(B2H)=tr[B2·P·diag(q1,q2,…,qp)·P′]= 其中,b11,…,bii,…,bpp为P′B2P的主对角线元素. tr[(C+σ-2εε′)H(C+σ-2εε′)]=tr[(C+σ-2εε′)2H]≥ tr[C2P·diag(q1,q2,…,qp)·P′]= 其中,c11,…,cii,…,cpp为P′C2P的主对角线元素. 由定理2的证明可知 故 即 定理4设n阶方阵T的秩为Rank(T)=p,X′T′TX的特征值为λ1≥…≥λp>0,TT′的特征值为h1≥…≥hp>0,k1≥…≥kp≥0,0≤dp≤…≤d1<1,则 (13) 证明类似于定理2的证明,略. 定理5设n阶方阵T的秩为Rank(T)=p,X′T′TX的特征值为λ1≥…≥λp>0,TT′的特征值为h1≥…≥hp>0,H的特征值为q1≥…≥qp>0,k1≥…≥kp≥0,0≤dp≤…≤d1<1,则 (14) 证明类似于定理3的证明,略.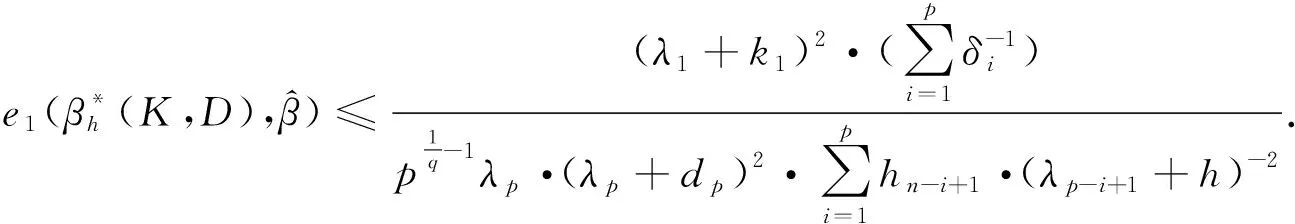
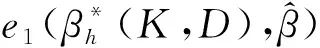
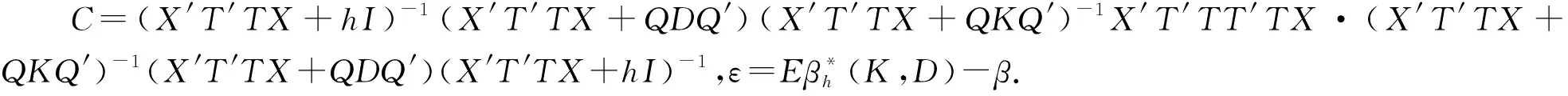
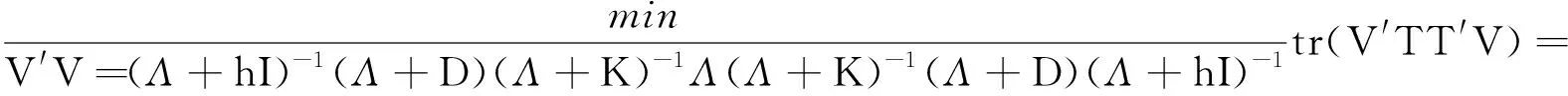
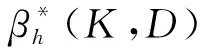
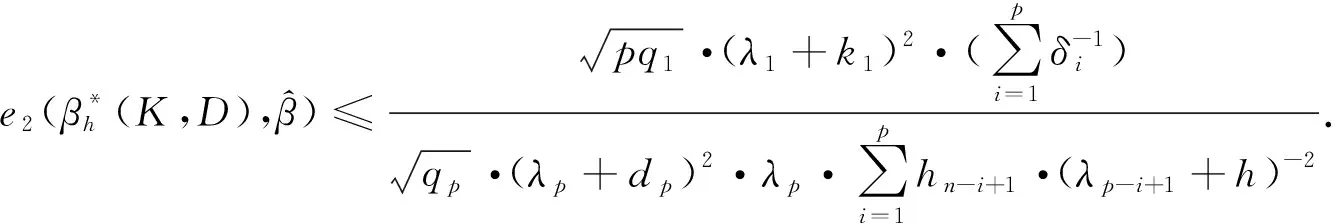
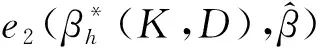
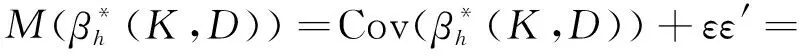
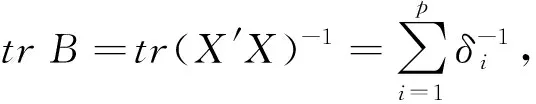
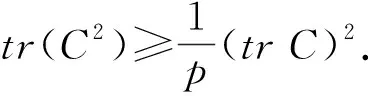
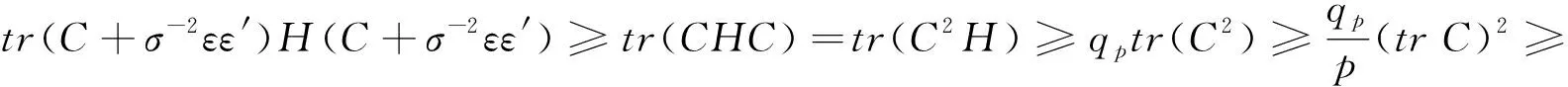
4 广义聚集双参数改进估计代替Peter & Karsten估计对的估计效率
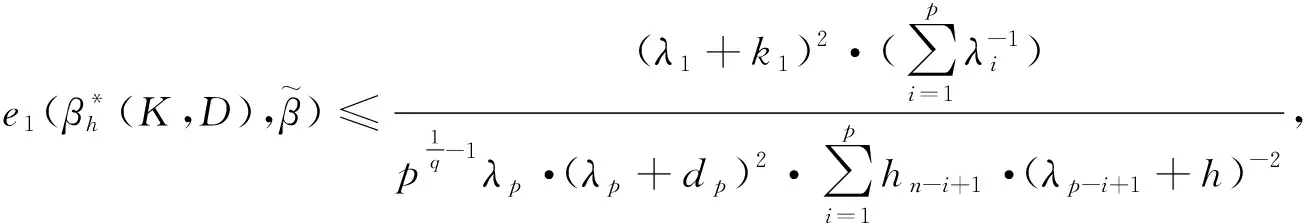
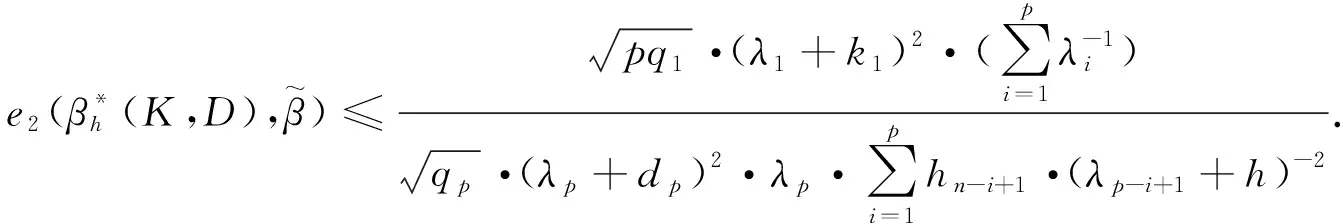
5 结论