Banach代数上的伪Drazin逆
2022-06-02 03:11王国栋陈焕艮
杭州师范大学学报(自然科学版) 2022年3期
王国栋,陈焕艮
(杭州师范大学数学学院,浙江 杭州 311121)
0 引言

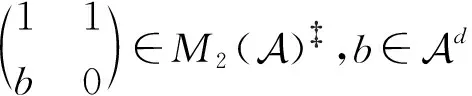
1 分块算子矩阵
首先,给出一些重要引理.

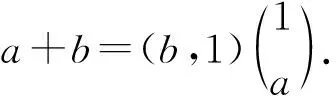

记







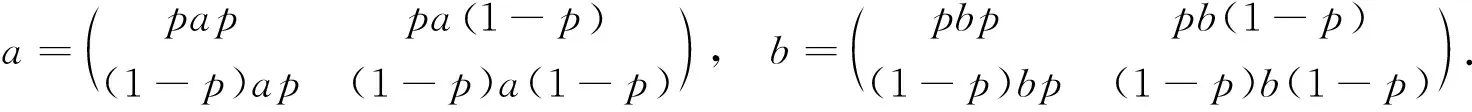
于是,

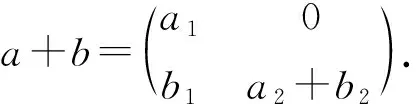











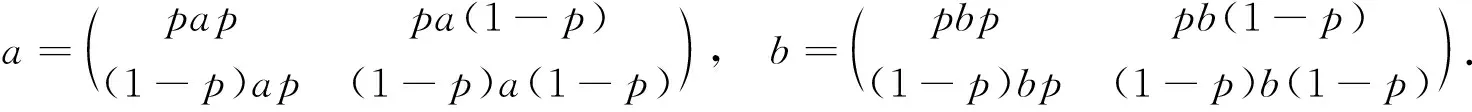
于是,
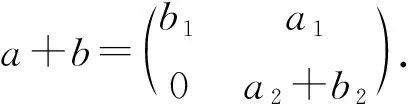
注意到













例 1设
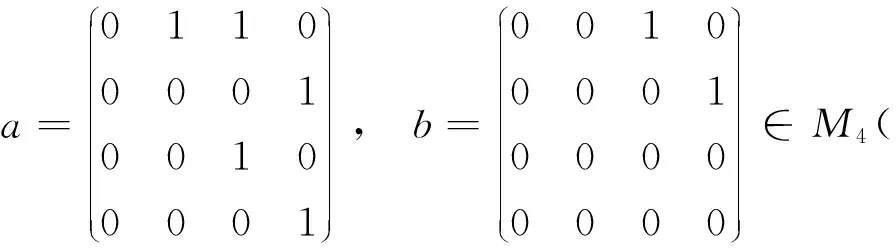
通过计算,有


2 反三角算子矩阵
这一节将探讨Banach代数上的反三角算子矩阵何时具有伪Drazin逆.首先,给出一个重要引理.
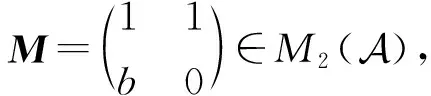
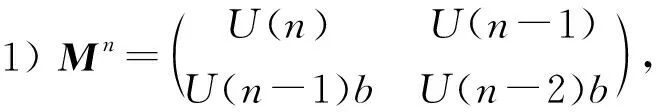
2)对任意正整数n,有U(n)-U(n-1)=U(n-2)b.
证明由文献[3,引理4.1.12]可得.
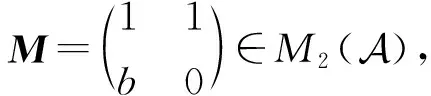

U(k+1)x2+U(k)x4≡U(k-1) (modJ(A)),
(1)
U(k)bx2+U(k-1)bx4≡U(k-2)b(modJ(A)).
(2)
在式(1)左边同乘以b,再减去式(2),得
U(k-1)b2x2+U(k-2)b2x4≡U(k-3)b2(modJ(A)).
(3)
类似地,可以得到
(1+b)bk-1x2+bk-1x4≡bk-1(modJ(A)),
(4)
bkx2+bkx4≡0 (modJ(A)).
(5)
于是,
bk≡bkx2+bk+1x2+bkx4≡bk+1x2∈bk+1A.
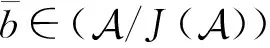



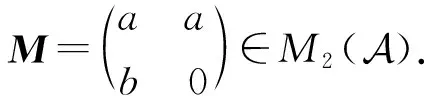

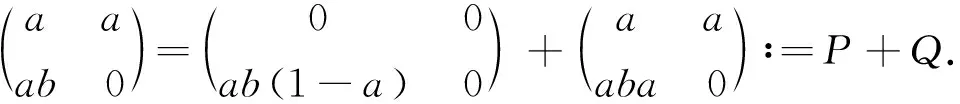

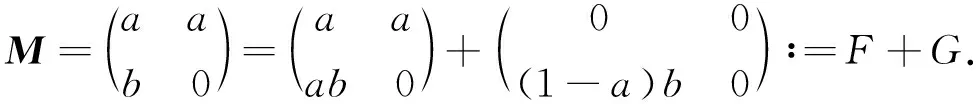

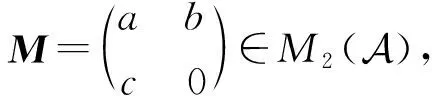
证明⟹.考虑分解
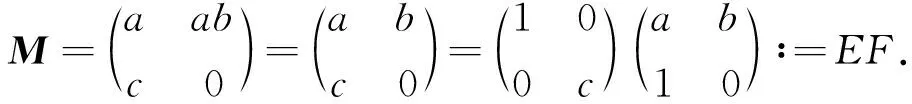
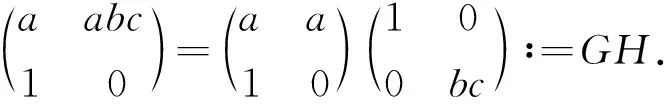
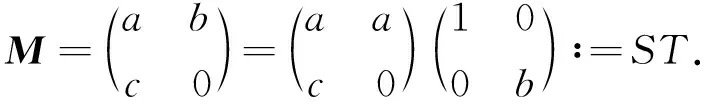

设
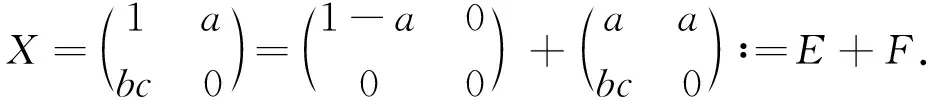

令
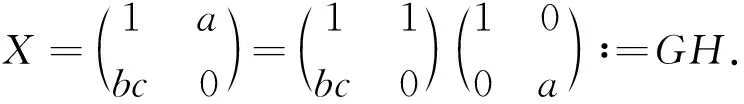


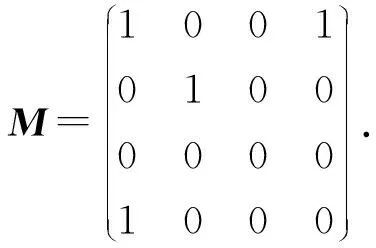
猜你喜欢
房地产导刊(2022年4期)2022-04-19
黑龙江大学自然科学学报(2022年1期)2022-03-29
山东农业工程学院学报(2020年12期)2020-03-19
中等数学(2019年8期)2019-11-25
长江丛刊(2018年8期)2018-11-14
中学数学研究(广东)(2018年13期)2018-08-11
中等数学(2018年12期)2018-02-16
商情(2017年9期)2017-04-29
大陆桥视野(2016年14期)2016-12-27
环球市场(2016年14期)2016-11-28

