导数视角下双变量问题的多角度处理方法
浙江省杭州学军中学海创园校区 (311121) 陶勇胜
在近些年高考压轴题中,以导数为背景的双变量问题一直是导数题中的热点和难点[1].这一类问题因含两个变量,其解法众多且技巧性强,常以压轴题形式出现,对学生的数学抽象、逻辑推理、数学建模等核心素养有较高的要求.本文从一道2021年全国高考题说起,对导数视角下双变量问题进行多角度探究,以期优化解决此类问题的思维策略.
一、构造函数角度
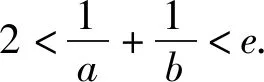
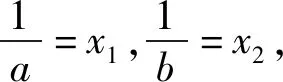
证明:(1)f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,过程略.
下面证明:2 证法1:(利用对称,构造函数)令F(x)=f(1+x)-f(1-x),其中0 评注:证明不等式x1+x2 “数少形时少直觉,形少数时难入微”,数形结合是解决函数及导数问题的重要思想方法,下面从数形结合角度谈谈处理双变量不等式问题. 图1 图2 评注:2015年天津理科卷第15题用双切线代替曲线[1]及2021年全国新高考Ⅰ卷第22题(例1)用切线、割线代替曲线[5]证明双变量不等式,说明以直代曲的方法是处理双变量问题的有效方法之一. 这是一道双变量不等式证明的经典题,可以通过齐次化、比值代换、比差代换、增量法[2]-[5]等方法求解,下面从数形结合角度,以曲代曲的方法进行探究: 图3 图4 例5 题目同例1. (Ⅰ)不等式x1+x2>2的证明. (Ⅱ)不等式x1+x2 证法2:因为0 分析:(1)略;(2)本题是以导数为背景的双变量不等式问题,涉及函数、不等式和导数等众多知识,看似变量较多,实质是极值点偏移问题.欲证不等式2(x2-x1)>x5-x3,采用分析法,将目标进行等价变形,即要证明2x2-2x1>(x5+x4)-(x3+x4),只要证明x3+x4>2x1,x4+x5<2x2即可. 数学解题中,有些题目按常规解法较难,若更换观察角度,一动一静,主客换位思考,往往有“出奇制胜”的效果. 双变量不等式的证明是考查导数部分内容的一个重要抓手,导数与不等式等知识综合对学生的思维能力有很高的要求,深刻考查学生的综合能力和核心素养,通常以压轴题出现,因此,导数及其应用的处理应重视直观,数形结合,突出本质,关注过程,归纳通性通法,这就要求教师精选例题、习题,通过对典型例题进行多角度探究和适当变式,让学生深刻领悟问题的本质,掌握解决问题的一般方法和规律,体会其中蕴含的数学思想.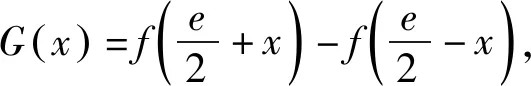
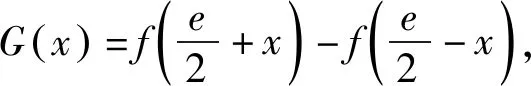
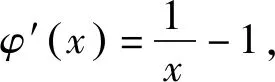
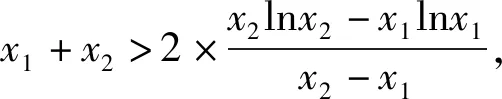
二、数形结合角度
1.以直代曲


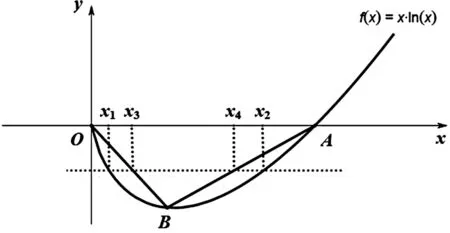
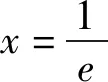
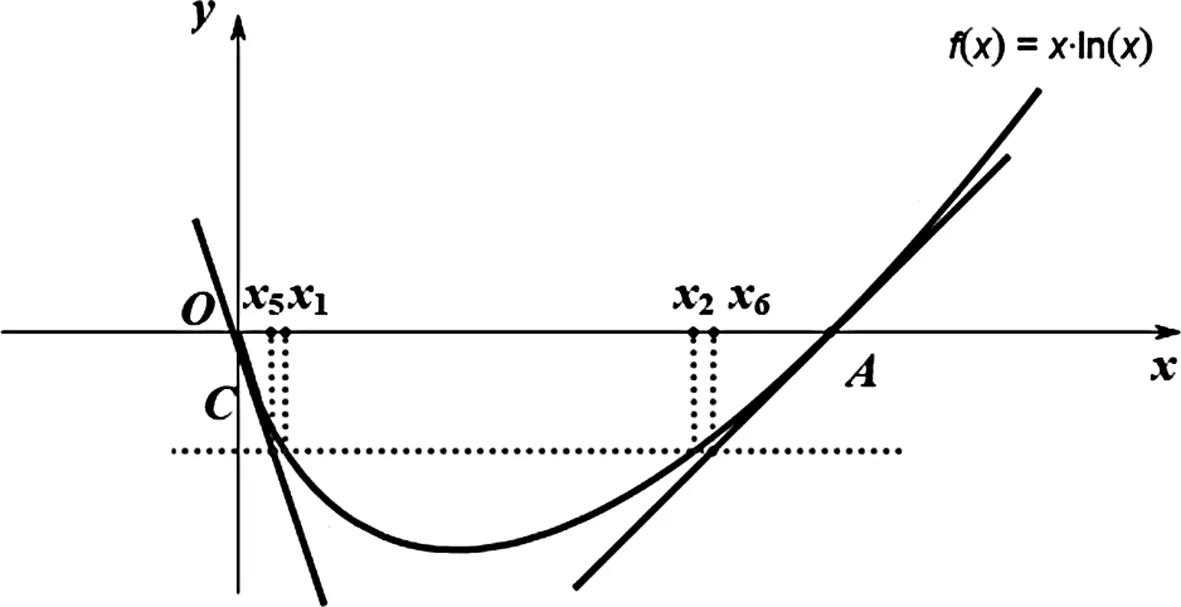
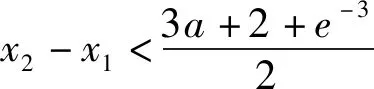
2.以曲代曲
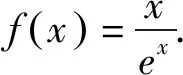
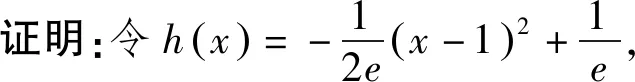
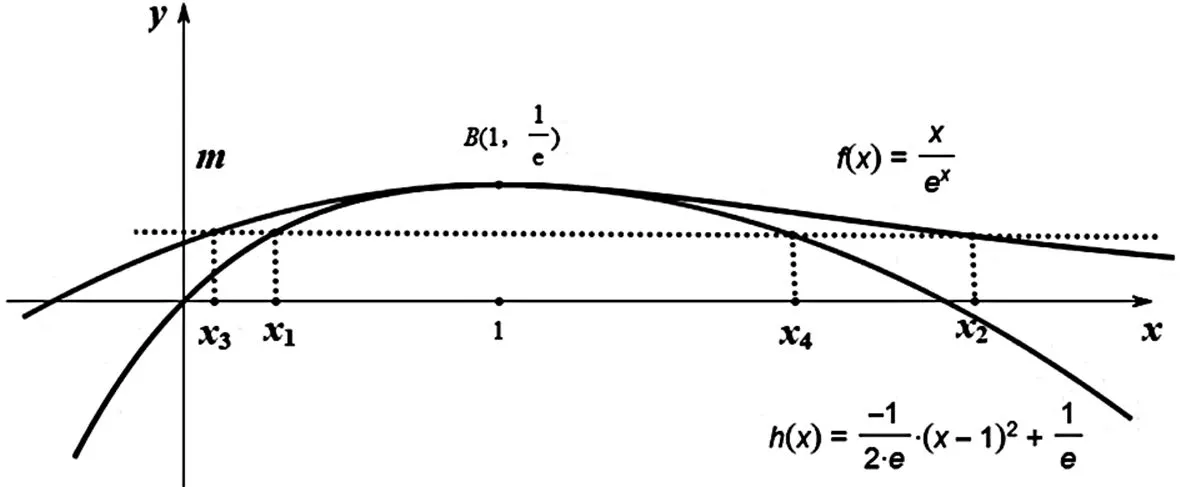
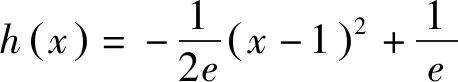
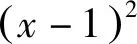
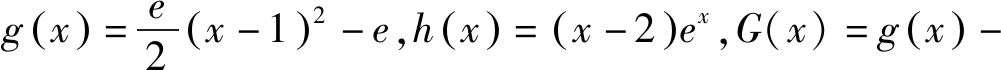
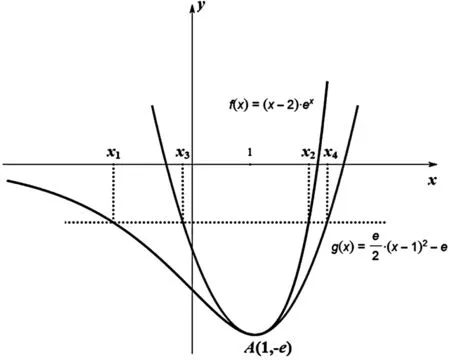

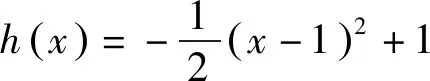
三、不等式放缩角度

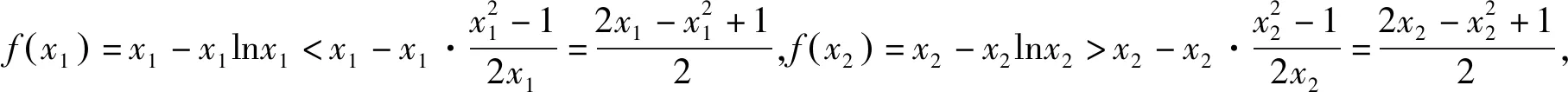
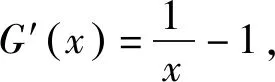
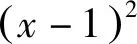
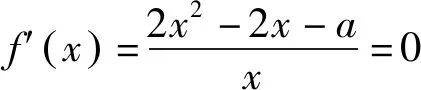
四、主元角度
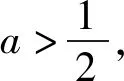
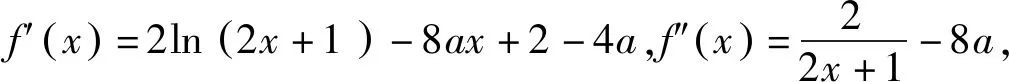
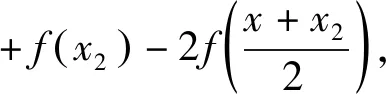
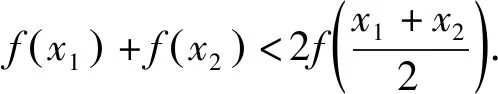
五、结束语

