以“问”导“思” 构建深度学习的小学数学课堂

张丽玲

“深度学习”是新课改的理念与追求。小学数学教师理应全面探索“深度学习”的本质内涵和具体目标，将其融入数学课堂，拓展学生的思维深度，并利用有效的教学问题引导学生独立思考，合作交流，让他们理清数学知识之间的内在关系，通过知识迁移、思维转换等不同的方式，向深度探索的目标迈进。本文以真实的课堂教学经验为基础，对问题导向背景下小学数学深度学习的必要性进行分析，并从层次化问题、生活化问题、链条式问题等方面，探索了小学数学教学中以“问”导“思”的具体路径，以期达成深度学习的教学目标。

一、构建“以问导思的深度学习小学数学课堂”的必要性

“深度学习”是新课改积极倡导的理念与追求。数学深度学习，要从理解起步，“深”在学习内容的内涵与本质，“深”在知识学习的过程与方法;强调以学为中心，以深度探究、深度思考为特征;指向学生问题解决能力的培养和高阶思维的发展。小学数学教师理应在把握“深度学习”本质内涵的基础上，努力探寻达成“深度學习”的有效路径。古语有言：“学起于思，思源于疑。”小学生是一个对外部世界具有强烈探索欲望和好奇心的群体，为了契合小学生的特征和身心成长规律，以“问”导“思”，以“问”导“学”，建构深度学习课堂成了必要选择。教师要担当起领路人的角色，以导学和启发式的教学策略，让学生在质疑中思考，于思考中探索，从而增强学习的深度和探究的广度。因此，教师教学时，应紧扣知识本质，以问题为导向，依据学生的真实思维水平，设计环环相扣的教学问题，引领学生的思维发展，驱使他们在思考和探究的过程中达成深度学习的目标，进而培养学生的独立思考能力和深度学习素养。

二、以问题为导向，构建小学数学深度学习课堂的路径

（一）巧借层次化问题，满足学生个体需求

在新时代背景下，我国倡导培育具有创新精神和实践能力的人才，为了顺应主流化的教育趋势，中国个性化教育执行院长曹晓峰教授提出了“个性化教育”的理念，强调了教育目的、过程、结果和前提的个性化，这便为构建小学深度学习的课堂提供了思想指导。教师可以融合“个性化教育”的理念，针对学生间的个性差异，设计导向性和层次化的问题，让学生在针对性问题的引领下，主动展开探索和论证，找准解决数学问题的具体路径，如此，学生的个体需求得以满足，他们的深度思维也能逐渐增强。

教师以学生的个体需求为依据，设计层次清晰的数学问题，将数学概念、定理等元素进行细化和解读，让学生在层次递进的问题情境中，产生主动思考和自主探究的欲望，并在论述问题和解决问题的过程中，逐步消解自身的畏难情绪和抵触心理。例如，在“平行四边形和梯形”的教学中，教师从个性教育的视角出发，将学生分为A、B、C三个层次，A层次对应逻辑思维和解题能力较强的学生，B层次对应数学思维和学习能力皆处于中等水平的学生，而C层次则可以对应学习积极性和综合水平都不高的学生。待明确了学生的具体层次后，教师在课堂中引进与之相契合的教学问题，发挥层次化问题的引领作用。

C层——基础性问题。从上述分析中可知，C层次学生在学习积极性和综合能力方面相对薄弱，依据这一情况，教师设计的问题应以基础知识为主，引领学生明确基本的数学概念，增强他们学习数学知识的信心，稳步提升思维能力，为后续的深度学习打下坚实基础。比如，以“平行四边形的对边有怎样的特征？平行四边形有几条高？梯形呢？”等涵盖基础概念的问题，引领学生巩固知识，让他们在问题的启示下，明晰“平行四边形”和“梯形”的基本特征和性质。

B层——启发性问题。针对B层次学生的真实思维特征，教师在课堂中展开提问，可以同时呈现出多元化的选择，让学生在对比分析和思辨的过程中，明确数学概念的正确表达方式。比如，教师在课堂上针对B层次的学生提出以下问题：“以下三句话中有一个是正确的论述，你能找出来吗？1.四边形也是梯形;2.梯形是特殊的平行四边形;3.梯形有无数条高。在一个问题中涵盖了三个元素，学生将这三个元素与梯形和平行四边形的概念、性质进行对比，排除其中的错误论断，在对比和排除错误论述的过程中，学生的多元思维以及对数学概念的理解也得到了强化。

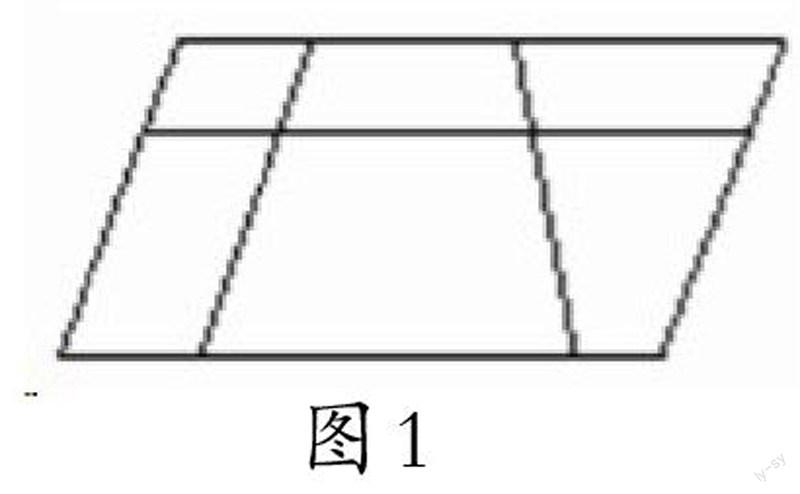
A层——拓展性问题。处于A层次的学生，他们已经对基础理论和概念等有了一定了解，所以在提问时，教师应以新颖和开放式的问题，激活学生的创新思维，让学生围绕着数学知识的内核，不断延伸思考范围。在课中教学阶段，为了让学生正确甄别“平行四边形”和“梯形”，启发学生的直观想象思维，教师可以设置图文结合的问题，在多媒体设备中出示图形（如图1），并提出问题“下列图形中，共有______个平行四边形，有________个梯形”。

在该问题的启示下，学生会主动思考“平行四边形”和“梯形”在概念、外形等方面的差异，并在图形的辅助下，形成直观想象思维，从创新化的角度解读问题。在此基础上，学生细致甄别二者的概念，通过标记法，得出答案“共有9个平行四边形和9个梯形。”由此，学生的深度思维得以形成，他们也能从创新化的角度思考和论证数学问题。在以“问”导“思”的数学教学模式中，教师从学生已有的知识经验、数学水平出发，设计层次化的问题，借助这一方式，具有不同思维水平和解题能力的学生，能在自身现有能力的基础上展开思考，所以，后进生巩固了基础、中等生提升了能力、优秀生增强了创新思维，以此为基础，数学课堂也初显深度学习的特质。

（二）利用链条式关联问题，推动学生自主思考

构建深度学习的课堂，要依托于学生的思维发展和学生具备自主思考的意识，而思维发展过程是一个阶梯递进的趋势，教师要多维度引领学生思考和探究。基于此特征，在以“问”导“思”的课堂模式中，教师可以利用关联式的问题，以阶梯递进的方式，引领学生展开思考，让学生在问题串的启发下，理清数学知识的内在关联，建构起网格化的知识体系，形成系统化的认知结构，久而久之，学生不仅形成了深度思维，他们还能在深度思考的过程中增强解决问题的能力。

1.利用链条式问题，理解数学概念

概念教学是数学课堂上的基础性内容，也是实现深度学习目标不可或缺的教学环节。传统的概念教学存在一定的机械性，学生对概念的理解不够透彻，因此，教师要改变概念教学的形式和内容，以链条式问题引领学生明确数学理论的具体构成部分。如在“圆”的教学中，认识完圆各部分名称后，教师可以设置如下问题串引领学生进一步认识圆的特征：

（1）沿着任意一条直径对折，你发现了什么？

（2）观察折痕，圆有多少条半径？

（3）量一量各自画的圆内多条半径，你有什么发现？

（4）同一圆内，半径和直径的长度有什么关系？

从“问题1”到“问题4”，教师以层层深入的形式引出问题，引导学生针对“圆”的性质和特征展开思考，在关联式问题的帮助下，学生在画一画、折一折、量一量、比一比的过程中明确了圆的基本概念，并对半径、直径的内涵和本质有了准确了解。借此方式，数学课堂逐渐向着深度学习的方向迈进，学生的自主思考和积极探索的意识也明显增强。

2.利用关联式问题，探索解题路径

在概念教学基础上，教师还可以利用关联式的问题，引导学生探索解题路径，让他们在教师的循循引导下，形成有序解题的习惯和深度思维能力。比如，在六年级的综合复习中，根据应用题“某地出租车的收费标准为3千米以内收费7元，超出部分，按照每千米1.5收费，不足一千米的部分按照一千米计算”设计问题串，如下：

（1）如果你坐了6.5千米，你应该付多少车费？

（2）结合上述信息，完成下列的出租车价格表（表1）。

（3）除绘制价值表的方式，你还有哪些能够体现出租车收费分段特征的方式？

（4）怎样解决分段问题？它的核心要点是什么？

教学中，“解决问题”是课堂教学的重点，教师依据小学生的思维习惯和规律，提出了数学问题，并引导学生以数表结合的方式，制定分段计算的方案，让学生深入数学问题中的“点”，迁移到数学问题的“面”，探析高效解决问题的路径，并引领学生从不同的角度探索解题思路，使其朝着深度学习目标前行，进一步加强知识运用能力。

（三）设计真实性问题，激发学生探究热情

数学知识的抽象性和复杂性，为学生准确理解和扎实掌握知识带来了一定的阻碍。教学时，教师应结合生活实际，通过设计真实性问题的方式，从学生的现实生活中选取数学元素，让学生在真实案例和数学问题的启发下，自主调动生活经验，并灵活地利用数学知识解决生活问题，据此达成激发学生探究热情、提升其解决问题能力的目的。

例如，在“简易方程”的课堂教学中，教师以激发学生探究热情和构建深度学习课堂为目标，于课堂中提出与学生现实生活紧密相关的问题，达到启迪学生智慧、提升其创新思维能力的目的。

首先，回顾知识，启迪思维。在课堂的初始阶段，教师巧设生活情境，带领学生回顾旧知识，为后续的深度学习做好铺垫，启发学生的思考意识和深度思维。如“有个问题亟须同学们解决，老师于上周末前往书店购买书籍，付给了老板50元人民币，老板找给我29元，请问这本书的价格是多少钱？”这是一个与小学生现实生活息息相关的生活化问题，教师将自身代入到“购物者”的身份，引领学生代入到“书店老板”的身份，其探究热情明显增强，在此基础上，学生根据“减法”的运算规则，列出算式：50-29=21（元），准确回答了教师提出的问题;也有同学列方程解决：设这本书的价格为x元，列方程为50-x=29，求得x=21，同样解决了问题。

其次，加深难度，深度探索。通过设置生活化问题的方式，学生将自己代入到情境中，他们解决问题和创新思维得以启发，由此出发，教师依据本课的教学内容，合理地展开提问和追问。如“这本书受到了其他老师的认可，他们纷纷请求我代为购买，现在得知，该本书若购买超过10本，超出部分每一本比之前降价2元，老师一共花了381元，那么我一共买了多少本书呢？”在引出该问题后，学生利用“四则运算”方面的知识展开计算，列出算式：381-21×10=171，171÷（21-2）=9，10+9=19。随后，教师适时追问：“你们还有哪些更加简便的计算方法吗？可不可以利用方程知识解决上述问题？”通过追问的方式，学生转换了自身的思维模式，他们将生活化的问题与方程知识结合起来，据此，学生可以列出如下解题算式：

第一步：设教师一共买了x本书

第二步：根据给定信息，列出简易方程21×10+（x-10）×（21-2）=381

第三步：计算方程式，210+（x-10）×19=381→（x-10）×19=171→19x-190=171→19x=361→x=19

最后，阐释结论，互动交流。学生在生活化问题的辅助下，实现了由简单问题到复杂问题的过渡，他们掌握了迁移和应用知识的技巧，其思维发展呈现出由浅入深的态势。而为了进一步拓展学生的学习和思考深度，教师可以在学生得出结论后，引导他们以个人或小组为单位，阐释解题思路，说明应用了哪一部分的数学知识、在解题中遇到了怎样的困难等，在交流的过程中，学生之间共享信息、抒发感悟，他们能在多元思维的启示下，明确解答问题的多元路径，由此，学生不仅达成了深度学习的目的，也能增强思维的开阔性和创新性。

（四）运用反向性问题，达成深度学习目标

在学生建构知识体系的过程中，为了帮助学生达成深度学习的目标，教师还应着力建设智慧型的数学课堂，增强学生的逆向思维和解题能力。因此，教师可以运用反向性的教学问题，改换数学问题中的条件，带领学生走出思维误区，让他们在逆向问题的驱动下，补足知识结构中的空白。在教学的过程中不难发现，因为学生缺乏逆向思维的能力，在解决数学问题时出现偏差。针对这一现象，在“长方形与正方形”的教学中，教师可以设置正向和反向相结合的数学问题，首先，从学生的正向思维出发，设置问题“假如一个正方形的长度为4cm，宽度为3cm，那么其面积为多少？”让学生从正面展开思考和分析。由此出发，为了达成深度学习的目标，教师设置“一个正方形的面积为28cm2，已知其长比宽多3cm，那么它的长和宽分别为多少？”的反向问题，以此加深其思维深度。

总之，将问题作为驱动型教学的素材，以“问”导“思”，以“问”导“学”，是达成深度教学目标的必要选择。数学教师应认识到问题的驱动和导向作用，从教学实际出发，探寻数学课程内容与学生真实学习水平的链接点，精心设计具有个体特征和真实性的数学问题，让学生在思考中稳步提升数学思维能力，并以链条的方式，逐渐提升问题的难度和开放性，引领学生的思维发展，鼓励他們从不同的角度展开思考和探究，然后在问题的导向下，培养学生的学习能力，提升数学素养，向着深度学习的目标迈进。

（邱瑞玲）