感受不同计算方式 助力探究学习深入

杜曼曼

[摘  要] 引入不同的计算方式于三位数除以一位数首位不够除的教学活动，是一种明智之举，也是一种能够促进学生学习发生改变的有益尝试。为此，在具体的教学活动中，教师应努力挖掘知识之间的内在联系，让学生在不同的计算中体会到除法的计算原理，能够较好地掌握首位不够除的计算方法，让学习能够不断推进，不断深入。

[关键词] 计算方式;计算原理;学习深入;数学素养

三位数除以一位数首位不够除，对于小学三年级学生而言，理解是有难度的，掌握是缓慢的，建构也是很难一步到位的。因此，在教学这一内容的过程中，首先，教师要仔细研读文本，把握准除法之间的内在联系，精细地设计各个教学环节及学生的探究活动;其次，教师应学会灵活地引入不同计算方式，引领学生去分析、去思考、去提炼，使得他们能够自始至终积极地参与到除法计算原理与方法的探讨过程之中，最终使得他们可以建构三位数除以一位数的数学模型，也使得他们学习这部分知识的效益倍增。

一、感知不够除，显现合理性

三位数除以一位数，特别是被除数的百位上不够除的情况，对于学生来讲是一个难点，这就需要教师带领他们去攻克堡垒，突破难点，以打通前后除法学习之间的壁障，实现知识、技能、经验的贯通，使算理理解和方法领悟得到有效的归总，从而让学生能够更科学地感知被除数百位不够除的基本属性，领悟这类除法的计算原理和方法。对此，教师就得重视估算、笔算等多元化计算方式的整合，让整个学习活动变得更加智慧，充满理性。

师：通过前面练习题的巩固学习，我们认识到适当地把估算等不同的计算方式集合起来，能提升计算结果的合理性。希望同学们在平时的计算中多运用一些不同的计算方式。请继续看屏幕上的例题。

课件呈现，把刚才2个书架，闪烁变化，2变成4。

学生根据课件的变化，再度阅读例题，感知问题的变化。

生1：题目把2改成了4，只要这样就可以了，312÷4。

师：你们同意嗎？那这道除法的商大约是多少呢？

生2：312比400少，要除以4，商会比100小。

生3：商应该是两位数，也就是几十。

师：怎么不会是100多呢？又或者是一位数呢？

生3：不可能是三位数，三位数至少是100，那被除数应该最小是400，现在只有312，所以不可能是三位数。

生3：也不可能是一位数，一位数最大是9，检验的话是9×4，只有36，而题目是312÷4，所以也不会是一位数。

师：你的思路还是蛮开阔的，会通过检验来研究问题，这个方法值得使用。那就试试笔算，看看我们的思考是否合理。

学生自主进行竖式计算，并交流自己的所思所想。

三位数除以一位数首位不够除是三年级学生学习的一个难点，要突破这一难点、帮助学生打破首位够除的思维定式，教师就得精准地解读文本，把握这类问题发生的基础、发展的过程，理清知识的脉络，理顺知识之间的逻辑关系，进而突破难点，助推有效学习。

二、尝试竖式算，展露科学性

估算是一种检验除法计算结果合理性的辅助手段，要帮助学生正确建构三位数除以一位数（首位不够除）的数学模型，还得运用最基本的竖式计算。为此，笔者就利用第一阶段学习的思考成果，引导学生去尝试练习，使学生在试着列竖式的过程中，获得“首位不够除，就得和下一位合在一起去思考”的感悟，并在具体的试除计算中得到应有的学习体验，使得三位数除法的模型逐渐完善起来。

师：哎！大家怎么还没有动笔？是不是有什么难处？

生4：以前我们学过，除数是一位数，就得先看被除数的最高位的数，现在是3，可是3比除数4小，不够除，该怎么办？

生5：是啊！3除以4，不好除的呀！

……

师：这是个新问题。不过，我们刚才不是估算了吗，商是两位数的呀！那有没有其他办法来解决这个问题呢？

生6：我想，可以把312分成280和32两部分，这样先算280÷4，得到商是70，再算出32÷4等于8，合起来整体商就是78，商是两位数的。

师：这个方法真不赖！还有其他方法吗？

生7：我认为，可以把312分成310和2，31就是31个十，当310÷4时可以想成31个十除以4，得到7个十，余3个十，也就是余30，再把30与2合起来变成32，32÷4就是8，结果是78。

师：你真了不起！这样的思考过程，你们能理解吗？主要思考31个十在哪里，联系一下自己列竖式计算的情况，分析一番。

学生仔细看着自己所列竖式的初步样子，思考31个十在哪里。

生8：对！31个十除以4，商是7个十，在十位上才是7个十，到百位上就是7个百了。

师：分析得很到位，也很科学。你现在会继续做下去了吗？

学生自主用竖式计算312÷4，并与同桌交流自己的想法。

师：你的计算结果是否正确呢？应该怎么办？

生（齐）：验算，用商乘除数，看是不是等于被除数。

生（齐）：验算时也要注意，如果有余数，应该是商乘除数加余数，等于被除数。

……

案例中，首先，教师在学生遇到困惑时，没有直接讲解三位数除以一位数首位不够除该如何计算，而是采用问题引领的方式“我们刚才不是估算了吗，商是两位数的呀！那有没有其他办法来解决这个问题呢”让他们不再纠结于如何列竖式计算，而是发挥创新思维，寻找其他的突破途径。在集思广益之下，学生想到了把312进行拆分，分成240+72或280+32，再分别除以4。这样的操作，既能照应好估算学习，增强学生运用估算的意识;又能帮助学生打开学习视野，实现难点的化解，进而实现这类除法计算学习的突破。

其次，教师组织学生对31个十的观点进行研究探讨，以帮助他们科学地分解312，使其更加符合笔算除法的算理，以便他们利用这一学习成果去思考竖式计算。经过探讨交流、思维碰撞，学生能够感悟到其中的奥秘，理解笔算除法的本质，使得整个学习活动更有底气。

三、反刍全过程，凸显整体性

学习需要不断反刍，也正因为学生对学习过程不断地咀嚼，他们才能更精准地把握知识的本质，才能更好地构建相应的数学认知体系。在三位数除以一位数首位不够除的教学活动中，教师就得创设契合本班级学情、符合地域特点的学习情境、活动情境等，引导学生去解析一个个具体的算法，从中感悟到这些算理中的共性规律，进而提炼出首位不够除的一般规则，从而让他们的学习研究活动富有哲理，也使得整个学习有条理、成体系，成为一个有机的整体。

师：经过这么长时间的学习，你能独立地思考并完成下面的问题吗？

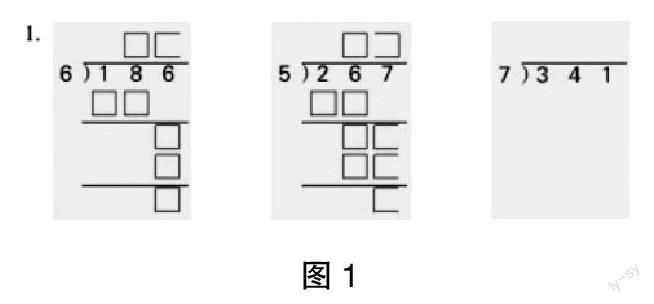
投影呈现“想想做做”的第1题（如图1）。

学生观察习题，尝试解决问题。

生9：第1小题是186÷6，首位是1不够除，这样就把十位上的8合起来成为18个十，除以6得3个十，所以在8的上面商3，这次计算没有余数。接着就直接计算6除以6，得到1，所以最后的商是31。

生10：第2小题和第1小题的情形差不多，也是被除数百位上的数比除数小，所以要看最前面的两位数，再按照除法的方法进行计算。

……

师：完成这三道习题，你的感触是什么？

生11：首位不夠除的除法，都必须先看前两位数。

生12：一定要把百位与十位合起来思考，是多少个十。

生13：第一步的商都是在十位上的。

师：现在你知道，为什么第一步的商要写在十位上了吗？把它说给你的同桌听听。

学生互动，交流自己对三位数除以一位数首位不够除的算理的理解。

师：总结得很到位，需要同学们好好记一记哦！复习一下，谁还记得除法中余数应该有什么特点呢？

生14：这个简单，二年级时就学习了，余数总比除数小。

师：能等于吗？

生15：不能！等于不是也可以再商1了吗？

……

指导学生进行反刍与相应的学习回顾，是加强学习理解，助推认知建构的有效举措。在小学数学教学中，教师要时刻关注学生的学习积累，努力通过多元化策略，促进他们梳理已学知识与自我反思，进而在群体的互助活动中，认知理解愈加深刻，认知构建更加牢固。

总之，在小学数学教学中，教师要做有心人，既要关注学情，准确地掌握学生的知识积累、经验储备以及数学思维的特性等情况;又要关注数学知识之间的逻辑联系，努力挖掘不同计算方法之间的互补性，以此助推学生对三位数除以一位数首位不够除的算理理解，掌握对应的算法，让学生更科学地积累笔算除法的经验，掌握相应的计算规则。最终，使学生的学习活动不断升级，学习实效不断提升，归纳能力等数学思维得到稳步发展，数学素养也得到不断提升。