共顶点相似等腰三角形问题的本质及其变式探究

林壮青 王海青

[摘  要] 几何是培养学生空间思维和想象能力的重要载体，也是中考的重要考点. 处理几何综合问题的关键是从复杂图形中找出常见的基本图形及其位置与数量关系，将复杂问题简单化，从而找到解決问题的思路和方法. 研究以共顶点相似三角形问题为例，探讨几何解题教学的路径与策略.

[关键词] 等腰三角形;几何教学;变式教学;相似三角形

平面几何综合问题是中考必考的压轴题之一，是初中中考复习的重点，也是难点，主要考查学生综合运用几何知识解决问题的能力，培养空间思维和想象能力. 处理几何综合问题的关键是从复杂图形中找出常见的基本图形及其位置与数量关系，将复杂问题简单化. 进而抓住问题的本质进行变式引申，通过一题多解、多题一解实现由一题通一类、由点带面的效果，帮助学生形成灵活完善的整体知识结构，促进学习的迁移. 而共顶点的相似等腰三角形问题频繁出现在近年来的中考试题中，下面以此类问题为例，按照波利亚《怎样解题》[1]的思想，探析如何开展有效乃至高效的数学解题教学，以提高学生解决问题的能力培养良好的数学思维.

题例

共顶点相似等腰三角形问题：如图1所示，△ABC是等腰三角形，AB=AC，△ADE是等腰三角形，AD=AE，且∠BAC=∠DAE=α°.

分析：上面三个图形只是两个等腰三角形的相对位置不同，可以看作是图形的变式，但本质一致，结论相同. 该图包含了丰富的平面几何知识，涉及全等三角形、相似三角形、角平分线以及圆的性质等，其关键就是两个相似的等腰三角形及其隐含的数量与位置关系，由此可以构建复杂多样的几何图形和相应的几何问题.

主要结论：以图1③为例得到图2，容易得到以下结论.

（1）△BAD≌△CAE;

（2）BD与CE相交于点F，有∠BFC=α°;

（3）AF 平分∠BFE;

（4）A，B，C，F四点共圆，A，F，D，E四点共圆.

证明：（1）因为∠BAC=∠DAE，

所以 ∠BAC+∠CAD=∠CAD+∠DAE，∠BAD=∠CAE.

在△BAD与△CAE中，

AB=AC，

∠BAD=∠CAE，

AD=AE，

所以△BAD≌△CAE（SAS）.

（2）由（1）知△BAD≌△CAE，所以 ∠11=∠10，∠AOB=∠COF（对顶角相等），∠1+∠AOB+∠11=180°，∠3+∠COF+∠10=180°，∠1=∠3，即∠BFC=α°.

（3）过点A作AG⊥BD于点G，作AH⊥CE于点H，如图3所示.

由△BAD≌△CAE知AG=AH，所以AF平分∠BFE.

（4）如图2所示，由（2）知∠11=∠10， ∠AOB=∠COF，所以△AOB∽△FOC，=.

因为∠BOC=∠AOF（对顶角相等），所以△BOC∽△AOF，∠8=∠9.

因为AB=AC，所以∠8=∠ABC，∠ABC=∠9.

因为∠1=∠3，所以∠9+∠3+∠ABC=∠8+∠1+∠ABC=180°，所以A，B，C，F四点共圆.

同理可证A，F，D，E四点共圆.

变式探究

以共顶点相似等腰三角形的问题及其图形为原型，可以生发出一类重要的平面几何问题，解决问题的过程突出体现了“截长补短”的方法策略与其蕴含的构造、转化与化归的重要数学思想.

变式1：（将图形条件特殊化）：如图4，点D为等边三角形ABC的BC边外一侧的一点，AD交CB于点E，∠ADB=60°，求∠ADC的度数.

分析  对于九年级的学生来说，比较简便的方法是先证明四点共圆，再利用圆的性质即可得到结果，也可以运用相似三角形的性质. 对于七八年级的学生，则需通过构造全等三角形利用相关性质来达成对问题的解决. 本题本质上还是共顶点相似等腰三角形问题.

解答  解法一（利用圆的性质），如图5所示，构造△ABC的外接圆☉O，在弧AB上任取一点C′，连接线段AC′，DC′，BC′.则∠AC′B=120°. 因为∠ADB=60°，所以∠ADB+∠AC′B=180°，所以A，C′，D，B四点共圆. 在等边三角形ABC中，∠CBA=60°，所以∠ADC=60°（同弧所对的圆周角相等）.

解法二（利用“反八字相似模型”或“蝴蝶结相似模型”构造相似三角形），如图4所示，AD交CB于点E. 在等边三角形ABC中，∠ACB=60°，且∠ADB=60°，所以∠ADB=∠ACB，∠AEC=∠BED（对顶角相等），△AEC∽△BED，=（相似三角形对应边成比例），=. 因为∠CED=∠AEB（对顶角相等），所以△ABE∽△CDE（SAS），∠ADC=∠ABC=60°（相似三角形对应角相等）.

解法三（截取长线段构造全等三角形），如图6所示，在AD上截取AF=BD，并连接CF，且在等边三角形ABC中，∠ACB=60°，AC=BC.

因为∠AEC=∠BED，且∠ADB=60°，∠CAE+∠AEC+∠ACB=180°，∠CBD+∠BED+∠ADB=180°，所以∠CAE=∠CBD. 在△ACF和△BCD中，AC=BC ，

∠CAF=∠CBD，

AF=BD，所以△ACF≌△BCD（SAS），CF=CD（全等三角形对应边相等），∠ACF=∠BCD（全等三角形对应角相等），所以∠BCD+∠FCB=∠ACF+∠FCB，∠FCD=∠ACB=60°，△DFC是等边三角形，所以∠FDC=60°，即∠ADC=60°.

解法四（补长短线段构造全等三角形），如图7所示，延长DB至点F，使DF=DA，连接AF，且∠ADB=60°，所以△ADF是等边三角形. 所以AF=AD，∠FAD=∠AFD=60°.

在等边三角形ABC中，∠CAB=60°，AB=AC，所以∠CAB=∠DAF，所以∠BAF+∠BAD=∠CAD+∠BAD，即∠BAF=∠CAD.

在△ABF和△ACD中，因为AC=AB，

∠BAF=∠CAD，

AF=AD， 所以△ABF≌△ACD（SAS），∠AFB=∠ADC，所以∠ADC=∠AFD=60°.

小结  解法三、解法四、解法五就是用“截长补短”的思想构造全等三角形，从而还原出题例“共顶点相似等腰三角形”的几何图形的原型. 将本题的结论改为“证明：AD=BD+CD”，或将题目的条件“等边三角形”改为“等腰直角三角形”“一般的等腰三角形”，将问题逐步一般化，解决过程一样. 如以下四个变式问题.

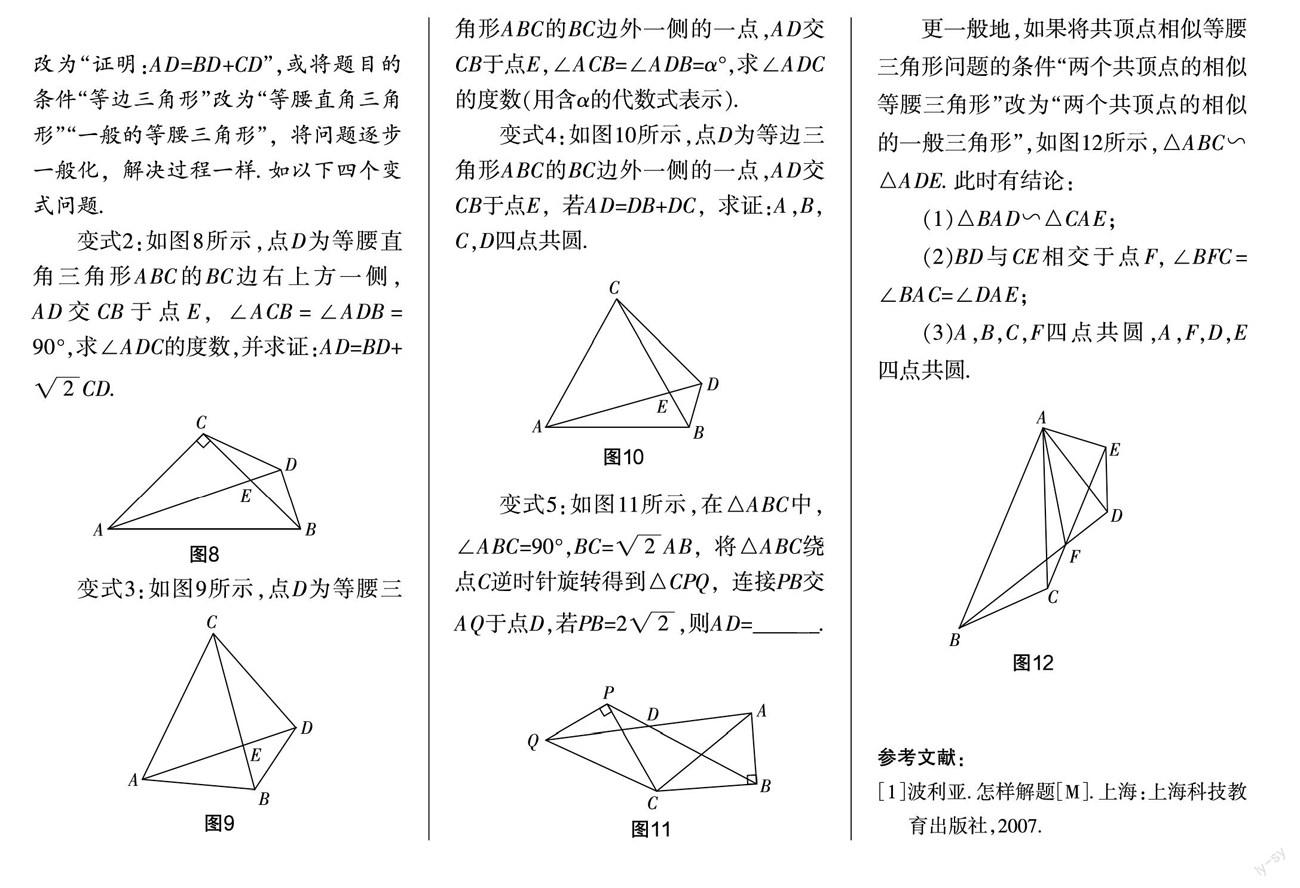
变式2：如图8所示，点D为等腰直角三角形ABC的BC边右上方一侧，AD交CB于点E， ∠ACB=∠ADB=90°，求∠ADC的度数，并求证：AD=BD+CD.

变式3：如图9所示，点D为等腰三角形ABC的BC边外一侧的一点，AD交CB于点E，∠ACB=∠ADB=α°，求∠ADC的度数（用含α的代数式表示）.

变式4：如图10所示，点D为等边三角形ABC的BC边外一侧的一点，AD交CB于点E，若AD=DB+DC，求证：A，B，C，D四点共圆.

变式5：如图11所示，在△ABC中，∠ABC=90°，BC=AB，将△ABC绕点C逆时针旋转得到△CPQ，连接PB交AQ于点D，若PB=2，则AD=______.

更一般地，如果将共顶点相似等腰三角形问题的条件“两个共顶点的相似等腰三角形”改为“两个共顶点的相似的一般三角形”，如图12所示，△ABC∽△ADE. 此时有结论：

（1）△BAD∽△CAE;

（2）BD与CE相交于点F，∠BFC=∠BAC=∠DAE;

（3）A，B，C，F四点共圆，A，F，D，E四点共圆.

参考文献：

[1]波利亚. 怎样解题[M]. 上海：上海科技教育出版社，2007.