以问题为导向，培养初中生的“生长点”

徐宝花

[摘  要] 教学中采用问题为导向，开展基于问题的学习任务，通过层层递进的问题深入思考，可以有效提升学生的理解层次，达到提高学生学习效率的目的.

[关键词] 数学问题;理解层次;思维

数学专题复习课是学生巩固基础知识和基本技能的有效平台，如何在复习课上提高复习效率，更好地寻找学生的生长点是教师教学中需要深入思考的问题. 而如何让专题复习课避免落入单纯讲题的俗套，发挥更大的效用，是提高教学效率的关键. 笔者认为通过设计不同层次的问题，让学生一步步深入理解，由点触面，进行知识迁移，可以培养学生的生长点，激发学生的思维，提高学生的学习效率. 本文拟以试题讲解为例，通过不同层次的问题设置，探讨如何培养学生新的生长点，供大家参考！

梳理试题，考查之“绳”

案例1  如图1所示，直线AB和CD平行，从函数的要素和图形的位置关系的角度，说一说它们之间的关系.

（学生从函数的解析式、解析式中的系数等方面进行了讨论和交流）

设计意图  本题教师并没有从常规的概念知识复习入手，而是渗透数形结合的思想，从数和形两方面归纳两条平行线的关系. 在讨论过程中，学生既需要观察图形，分析图形反映的信息，又需要结合函数知识，考查自身对于这幅图形的熟悉程度，为接下来的进一步学习打下了基础. 在问题设计中，教师采用的是开放式的设问，有利于培养学生的发散思维，更重要的是由图形抽象出函数解析式，培养了学生识图、联系、判断的能力. 学生在进行解析时，必须紧紧依靠这幅图形，从图形中的信息用数学语言进行解说，这就能突破课本知识和已有思维的局限，衍生出新的“生长点”，对平行线的性质产生新的认知.

数学基础知识的复习往往容易沦为数学概念的简单罗列，复习之后和复习之前在学生头脑中仍然是一样的零星散落，没有能构建知识体系. 同时，无法将课标中对于数学概念的掌握落到实处. 本节课通过函数图形的方式将平面直角坐标系和几何中直线的平行串联起来，让学生在回忆有关平行线的内容时有了依托，并且由于需要将函数与图形相结合，也就超出了单纯复习知识的程度，自觉地在大脑中将其进行了运用，提升了技能.

挖掘试题，题外之“问”

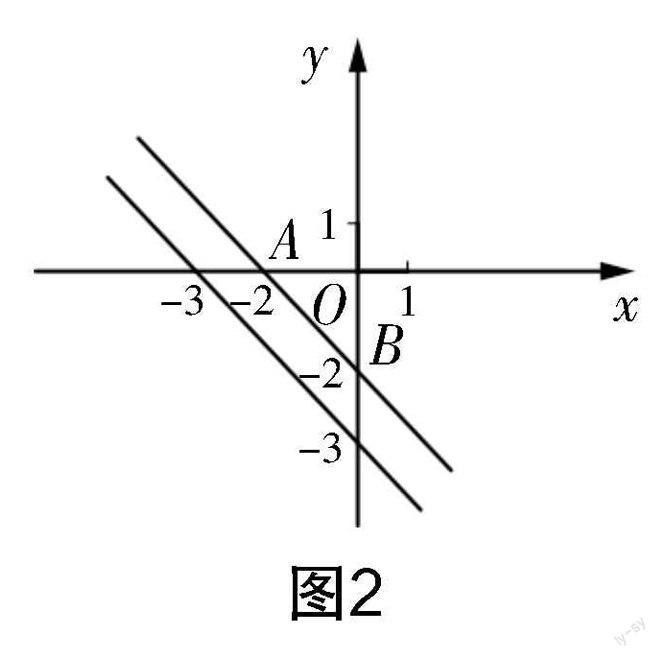
案例2  如图2所示，在平面直角坐标系中，直线y=-x-2与x轴和y轴分别相交与点A和点B，如果直线l与直线AB平行，那么要增加一个什么条件可以确定直线l的解析式？

（学生讨论交流之后，形成了一些方案）

生1：只要直线l可以经过一个已知点，就可以确定它的解析式.

生2：我觉得如果知道直线l平移的方向和距离，就可以确定解析式.

生3：我们小组讨论的方案是已知两条直线之间的距离，可以确定其解析式.

设计意图  开放式提问可以调动学生积极参与課堂活动，激发学生思维，但是教师也要做好充分的预设，预想出学生答案的多样性，做好课堂把控的准备，否则教学的走向也容易偏离教学目标，浪费教学时间.

复习课中最怕的是落入无限讲题的俗套和循环往复的“题海”战术，那样只会消耗学生学习的热情，对数学产生厌倦. 在复习课上教师可以通过试题的改编，让学生不局限于一道题，通过结论和条件的互换，由“条件”变“问题”，通过问题的派生，让“问题”产生新的“条件”，在不断训练中培养学生举一反三的能力，拓宽学生思维的广度. 因此在教学中，教师要敢于打破常规，由一题衍生出新题，以原题为基点，进行扩充，训练学生思维的灵敏度，提高学生的学习效率.

催生试题背后的疑问

案例2中学生提到的前两个解决方法同样地都采取了待定系数法，但是对于生3提出的方法，学生们争论不休，各执一词……

师：下面老师给第三种答案一个固定的数据，同学们来算一算这个解析式怎样求解. 我设这两条直线之间的距离为1个单位长度，请大家试着算一算，同桌之间进行讨论，期待你们的答案.

（学生之间有的讨论，有的开始执笔计算）

师：有的同学已经有结果了，我们一起来看一看.

生4：这样的直线有两条，我们可以过点A作一条直线AC与l垂直，垂足为C，如图3所示，这样得到△ADC和△BAO相似，利用=，可以算出AB的长度为2，AD的长度为，因此可以得到点C的坐标为

-2-，

-，由于点C在直线l上，可以得到直线l的解析式为y=-x-2-，根据对称性原理可以知道另外一条直线的解析式是y=-x-2+.

师：很好，那么有没有同学有其他的想法？

生5：我是用其他方法做的，我选了直线AB和x轴的交点A，然后过点A作直线AC垂直于直线l，垂足为C，这样出现Rt△DOE与Rt△AOB相似，由于AB和DE平行，那么△AOB就成为等腰直角三角形，所以△DOE也是等腰直角三角形，可以得到点D的坐标是（-2-，0），由于点D在直线l上，可以得到直线l的解析式为y=-x-2-，另外一条直线的解析式是y=-x-2+.

生6：我还有不同的做法，我选了直线AB和y轴的交点B，过点B作直线BC垂直于直线l，这样出现△DOE与Rt△AOB相似，由于AB和DE平行，那么可以得到△DOE是等腰直角三角形，得到点E的坐标是（0，-2-），由于点E在直线l上，可以得到直线l的解析式为y=-x-2-，另外一条直线的解析式是y=-x-2+.

师：同学们的这三种解法都是正确的，你最喜欢哪一种呢？

生7：我比较喜欢生5和生6的解法，因为生4的解法有些复杂，而且位置也比较难确定，但是生5和生6则抓住了直线与坐标的特殊夹角，计算较为简便.

师：你说得很有道理，但是我也在想如果这里没有特殊的夹角该怎么办呢，还能这样解决吗？

（再次呈现出开放性的问题，请学生进行讨论）

设计意图  如何激发问题的有效生成，其关键在于教师下放权力，将问题思考的权利交给学生. 由学生自己提出的第三种解法，让学生感觉到了困惑，如果将两条直线之间的距离设计成整数，那么计算就变得困难;在直线上任意取点也有较大难度，正是学生思考中的疑难使课堂激发出更多精彩. 教师在此时进一步提出学生的困难，引导学生进行辨析，用思维的火花来激发学生，能培养学生解题的迁移能力和灵活变通能力.

在学生的讨论和交流中，逐渐产生出新的解决方法和解题思路，真正提升了学生的学习力. 学生在开放性问题中再一次思考如何突破坐标轴上特殊点的疑难问题，使课堂充满了灵动的智慧，自身的思路源源不断地得到了开发. 师生互动、生生互动的课堂，让深度学习得到了真正的发生，真正实现了教学相长.

生成解题感悟

案例3  如图4所示，在平面直角坐标系中，直线y=-x-1与x轴和y轴相交于点A和点B，如果直线l与直线AB平行，并且与直线AB的距离等于，请求出直线l的解析式.

设计意图  通过案例3，学生已经能够根据直线之间的距离求出直线的解析式，并且还能选择最佳的解决方式. 经过案例3中坐标轴特殊点的讨论，学生已经能够理解直线的距离不是设置为整数，而是设置为无理数的理由，找到了问题的“生长点”.

从学生的解答中教师可以看到，学生已经从设置为有理数还是无理数的困惑中，过渡到可以轻松地通过设置无理数获得有理数的结果. 在教师搭建的交流平台中，学生不仅进行了充分的讨论，而且对知识进行了归纳和总结，为进一步的深入学习打下了基础. 问题探究的过程中，学生进行了一次由疑惑到比较、討论再到释然的感悟之旅，收获到思维顿悟的成果. 这样的设计看似问题重复，实则是对学生已经获得知识成果的固化，让学生体会到“现学现用”的成功，并为后续的学习埋下了伏笔，可谓是“一箭三雕”.

教学感悟

问题是新思想、新方法诞生的温床，只有在解决问题的过程中，才能探索问题解决的路径和策略，不断衍生出新的“生长点”. 因此教师在教学中要不断生成动态问题，激活课堂的活力，彰显课堂的智慧，推动高效、优质课堂的生成.

数学复习课中更要注意对问题的设计，通过问题激发新的疑问，寻找新的解题思路，培养学生思维的灵活性和深刻性，让复习课上出别样的风采，激发学生对科学的追求和对数学学科的热爱，提高数学复习课的效率.