从“怎么做”走向“怎么想”，增强学生的思考意识

龚珑

[摘  要] 要促进学生数学思维的发展，必须让他们由“怎么做”转变为“怎么想”，增强他们的思考意识，并教给他们思考的方法. 文章结合教学实践，提出相应的策略，让学生从根本上消除机械模仿，逐渐由形象思维过渡到理性思维，进而提升数学核心素养.

[关键词] 怎么做;怎么想;追问;初中数学

学生讲解试题时，仅能讲出试题的解答过程，讲不出是如何想的;教师往往只关注学生解答试题正确与否，而不关心他们的分析过程. 久而久之，学生的思维缺乏脉络，解答试题一直处于模仿阶段. 笔者以为，要促进学生数学思维的发展，必须让他们由“怎么做”转变为“怎么想”，增强他们的思考意识，并教给他们思考的方法.

不断追问，激起学生的思考欲望

追问是在学生回答问题的基础上进一步提问，以使学生做进一步的思考. 当学生只讲解解答过程时，教师可以追问：题中的什么条件给了你启发？你是从哪里入手的？从这一步到下一步的依据是什么？这样的追问能促使学生展现思维过程，并解释过程的合理性.

案例1如图1所示，在矩形ABCD中，对角线AC与BD交于点O，过点C作BD的平行线，过点D作AC的平行线，两线交于点P.

（1）求证：四边形CODP是菱形;

（2）若AD=6，AC=10，求四边形CODP的面积.

师：哪位同学来讲一下这道题怎么做？并说明理由.

生1：对于第（1）问，因为四边形ABCD是矩形，对角线AC与BD交于点O，所以OD=OC. 因为DP∥AC，CP∥BD，所以四边形ODPC是平行四边形. 所以四边形CODP是菱形.

生2：对于第（2）问，因为四边形ABCD是矩形，所以∠ADC=90°. 因为AD=6，AC=10，根据勾股定理，得DC=8，所以△ADC的面积=×8×6=24. 所以△ODC的面积=×△ADC的面积=12. 因为四边形CODP的面积=2×△ODC的面积，所以四边形CODP的面积=24.

对于第（1）问，等学生完成试题的解答之后，教师可通过如下追问引导学生从矩形的对角线入手思考问题：判断四边形CODP是菱形时，你们采用的判定方法是什么？菱形的判定方法比较多，为什么要使用这一方法？这样追问能让学生发现矩形ABCD与菱形CODP之间的联系，即菱形CODP相邻的两条边（OC和OD）恰好是矩形ABCD对角线的一半，而矩形的对角线相等，所以OC=OD. 所以要证明四边形CODP是菱形，可采用“邻边相等的平行四边形是菱形”这一判定方法.

对于第（2）问，教师可进行如下追问：在求四边形CODP面积的过程中，最关键的是哪一步？为什么求出△ODC的面积是最关键的一步？为什么△ODC的面积是△ADC面积的一半？为什么四边形CODP的面积是△ODC面积的2倍？通过这一系列的追问，学生能逐渐厘清问题的转化过程. 只有厘清了△ODC的面积、△ADC的面积和四边形CODP的面积之间的关系，才能知道解决问题时应先求什么、再求什么.

强化分析，让学生掌握思考的方法

数学家乔治·波利亚强调解决数学问题分四步走：一是弄清题意;二是制订做题计划;三是实施计划;四是回顾解答过程，进行检验. 如果學生只会做，那么解答问题就直接从第三步开始. 其实，弄清题意是最基础的一环，在这一环节，学生能知道试题的已知条件是什么，由哪个条件可以推理出什么结论，将若干个条件结合起来又会产生什么新结论，以及试题所求是什么，要完成所求需要满足什么条件. 作为教师，应引领学生分析问题，并在教给他们分析问题的方法的同时，让他们掌握思考问题的策略.

1. 想已知条件，由因导果，培养正向思维

从已知条件出发，由因导果，这种思考问题的方法就是综合法. 采用综合法时，教师应引导学生读懂试题有几个条件，分别是哪几个条件，并让他们逐条列出来，一个都不能少. 接着，让学生根据这些条件推一些结论，逐步进入问题的核心，从而培养学生的正向思维品质.

案例2如图2所示，已知A（0，4），B（0，-6），C为x轴正半轴上一点，且满足∠ACB=45°，则点C的坐标为______.

思路1如图3所示，因为∠ACB=45°，要让45°这一特殊锐角发挥作用，就必须构造直角三角形，所以应先构造等腰直角三角形AHC（∠HAC=90°），然后构造“一线三直角全等模型”（EF∥OC，且HF⊥EF，CE⊥EF），利用三角形全等，即△ACE≌△HAF，得到FH=AE，再利用△OCB∽△DHB（HD⊥AB），得到BD与OC的关系，最后求出点C的坐标.

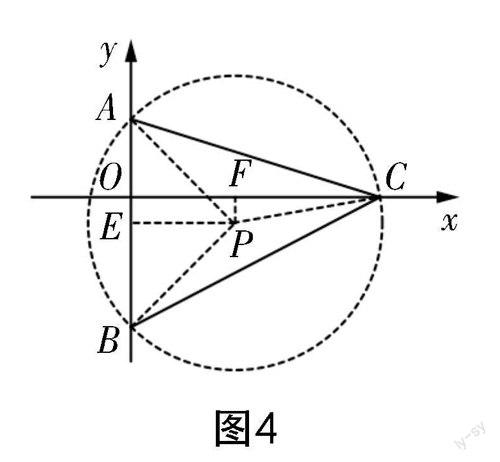
思路2如图4所示，因为∠ACB=45°是固定角度的角，∠ACB的对边AB=10也是固定的长度，根据定边定角必有隐圆，可以作出△ABC的外接圆☉P. 根据圆周角定理，得∠BPA=90°，可求得PE，PA，PB的长（PE⊥AB），进而可求得OF，PF的长（PF⊥OC），接着在Rt△PCF中根据勾股定理求得FC的长，从而求出点C的坐标.

思路3如图5所示，因为图形已经有一个45°的角，所以可以再构造一个45°的角（∠CDA=45°，点D在y轴负半轴上），以产生Rt△ODC和“母子型相似”结构. 然后设OC=x，利用相似三角形的性质，结合勾股定理，通过建立方程求出x的值，从而求出点C的坐标.

学生只有讲出分析过程，才能把每个条件的作用理解得透彻，也才能在不断的联想中发现不同的解题思路，从而产生智慧的火花. 此外，对比不同的解题方法，还能明晰解题方法的简与繁. 让学生由已知开始，有条理地联想与想象，有利于其思维的发展.

2. 想问题解决，执果索因，培养逆向思维

解题时，如果从已知条件出发思维受阻，学生此时不妨执果索因，想一想要解决的问题是什么、目标是什么、解决问题需要什么条件，顺着思路一步一步往前走，最终回到已知条件，实现问题的解决.

案例3民间流传李白买酒的歌谣：李白街上走，提壶去买酒;遇店加一倍，见花喝一斗;三遇店和花，喝完壶中酒. 试问酒壶中，原有多少（斗）酒. 你能回答这个问题吗？写出具体的求解过程.

思路从“三遇店和花，喝完壶中酒”往回逆推，知三遇店时有酒（1÷2）斗;那么，二遇花时有酒（1÷2+1）斗，二遇店有酒[（1÷2+1）÷2]斗;于是一遇花时有酒[（1÷2+1）÷2+1]斗，一遇店时即壶中原有酒的数量，应列式为[（1÷2+1）÷2+1]÷2=（斗）. 所以酒壶中原有酒斗.

从问题出发，逆向思考，实施的是正难则反的策略. 从案例3不难看出，有时通过逆推能轻松地解决问题. 这说明正难则反的策略在代数式化简、几何证明中均有重要的作用.

重视积累，夯实思考的基础

建构主义学习理论强调，学习过程是学生在已有经验的基础上获得新的经验. 学生原来的数学活动经验是思考的基础，是产生解题思路与方法的本源性经验，只有具有一定的知识储备，才能构建问题与所求结论的联系，从而实现重组与优化.

案例4已知方程组x+y=-7-a，

x-y=1+3a 的解x为非正数，y为负数.

（1）求a的取值范围;

（2）化简a-3+a+2;

（3）在a的取值范围中，当a为何整数时，不等式2ax+x>2a+1的解为x<1？

师：如何解答此题？

生1：先解方程组，求出x，y的值，再根据x为非正数，y为负数，建立不等式组，通过解不等式组求得a的取值范围.

生2：根据第（1）问求出的a的取值范围，可以去掉第（2）问中的绝对值的符号，从而化简代数式.

生3：因为2ax+x>2a+1可以变形为（2a+1）x>2a+1，要使不等式的解为x<1，必须满足2a+1<0，并结合第（1）问中求出的a的取值范围，得到a的最终取值范围，最后取整数值.

师：从本题的解答中，你们获得了什么解题经验？

生4：求方程组中字母的取值范围，要把问题转化为解不等式或不等式组.

生5：在有關不等式的问题中，要求字母的整数值，需要先求出字母的取值范围，再取取值范围内的整数值.

学生在解答本题时，将所求问题与方程组、不等式组的相关知识进行关联，通过解方程组、建立不等式组、解不等式组，解决了问题. 需要注意的是，在解题中，教师要引导学生经历与积累数学活动经验，如代数中的代入法、配方法、待定系数法、方程思想、函数思想等，几何图形中的图形变换思想、手拉手模型、“一线三直角”模型、轨迹思想等.

其实“怎么做”与“怎么想”之间并不矛盾，学生既要做好“怎么做”，更要做好“怎么想”. 只有弄清了思考的来源，才能获得解题的策略，懂得破题之道，从而从根本上消除机械模仿，逐渐由形象思维过渡到理性思维，而这也是数学教学之所求.