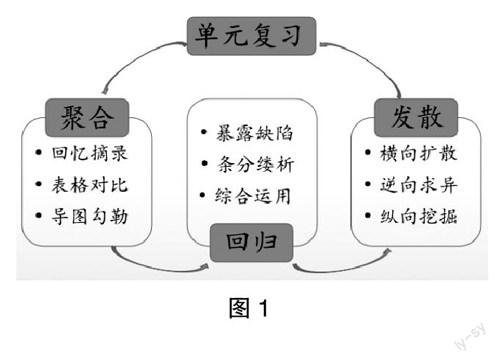
聚合·回归·发散：数学单元复习的实践路径

蔡林斐

［摘  要］ 复习课要启发学生的“聚合”“回归”与“发散”思维进行整体复习。关注知识间的关联，准确把握其生长点，注重思维的发散，达成概念的本质回归。向学生渗透事物间互相联系、互相依存的辩证思想，适当进行拓展与延伸，让知识的内涵与外延得到充分的解读与展示。培养学生有序思考、归纳整理的能力，推动学生在原有基础上进一步发展，在真实学习中进一步成长。

［关键词］ 单元复习；教学设计；策略探究

复习课，不能简单粗暴地套用新授课的模式，如果这样，势必让学生索然无味；如果疯狂刷题，也只能事倍功半。多年的实践经验证明，复习课，除了注重知识的梳理，关注各知识点间的关联，还要准确把握其生长点，进行综合性的巩固训练，适当进行拓展与延伸，让知识的内涵与外延得到充分的解读与展示，达成知识的本质回归。

一、聚合，厘清知识关联

“知识聚合”在这里包含两个层面：第一是“知识点的聚合”，从内容层面梳理一节课、一单元甚至一整册的知识，厘清各知识点之间的关联性和系统性；二是“数学方法聚合”，不仅仅是聚合某一个知识点的数学方法，更需要学会以数学思想方法为线索架构知识体系。基于以上分析与思考，“面积”复习课的教学实践可以借助思维导图的形式进行知识的聚合，来厘清知识间的关联。

（一）回忆式摘录，重现知识结构

就像电影里的闪回，用较短的时间将单元内容在头脑中回顾一遍，然后以摘记的形式呈现出来。回忆的过程就是一次知识的整理过程，这时候讲得再多、再生动、再细致也是徒劳的，教师必须舍得“浪费”时间。像“面积”单元的复习，面积和面积单位，长方形和正方形面积的计算，面积单位间的进率……一个个知识点都会在学生头脑中一一重现。这种机械式呈现，看似将知识碎片化了，但一旦经过大脑的作用，就会自动在一个个孤立的堡垒之间产生千丝万缕的联系。如讲到长方形和正方形的面积计算，当长方形的宽延长到与它的长一样时，就变成了正方形，所以说正方形实际上就是特殊的长方形。这个时候，教师只要给予学生充分的鼓励，给予学生更多的思考时间和表现机会，就能很好地建构起数学的知识结构。

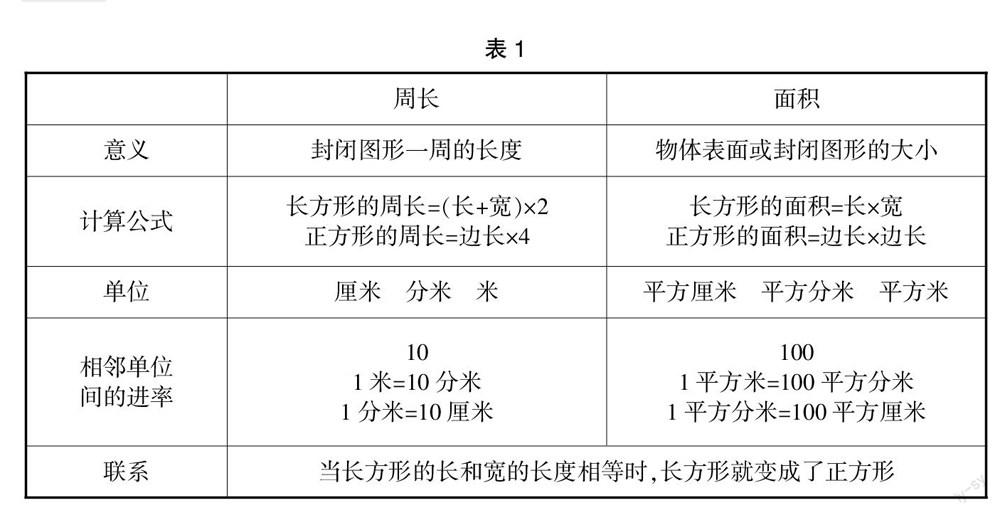
（二）表格式对比，厘清知识关联

制表梳理不失为一种较好的复习方法。从周长和面积的意义、计算公式、单位名称，到相邻单位间的进率，再到两者的联系，项项点点，清晰罗列，精准比较，使学生对于长方形、正方形的周长与面积的异同点、关联点一目了然（如表1）。通过自制表格对所要复习的内容已有所了解，课堂上学生急于表达自己复习时的收获和困惑。这个时候，教师可顺水推舟，将时间交给学生，让他们去展示交流。

通过交流，学生明白，关于意义的区别在于，周长是讲长度的，面积是讲大小的。面积的单位名称要在长度单位名称前加上“平方”两字。相邻单位的进率是10与100的区别，正方形就是特殊的长方形。当然，交流的形式可以不拘一格。可以先在小组内展开，因为学生在小组内的交流是最无拘无束的，最能将其真实的想法展示出来。然后，以小组汇报的形式，集中展示典型思想，其他学生可以从中得到及时的提醒和启发。学生在倾听的同时，也作合理的补充，真正实现“学学相长、共同提高”，这其实就是课堂上的一道亮丽风景。

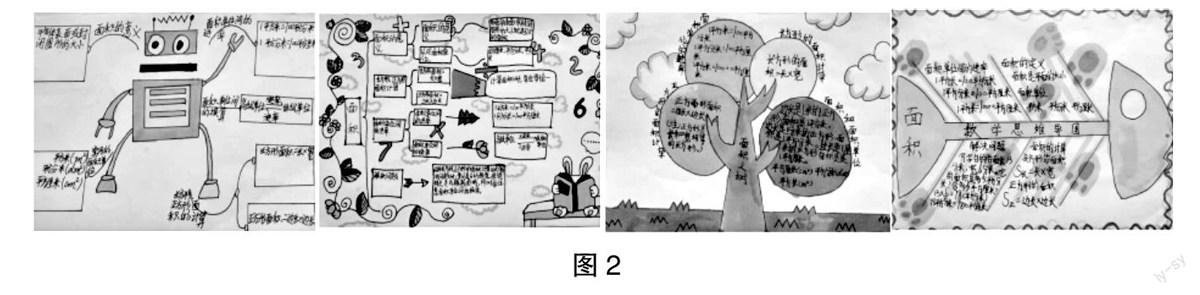
（三）导图式勾勒，形成合理认知

绘制思维导图的过程是使知识点形成知识网络的过程。教师要在复习课前就布置学生结合内容绘制思维导图，让他们自己先梳理知识结构，虽然制作思维导图不是件容易的事，是个循序渐进的过程，特别对于三年级的小学生来说，思维导图只是整理知识点的一种手段，他们绘制的思维导图可能很幼稚、不完整，甚至有错误，但是在绘制思维导图的过程中，他们经历了一场暴风骤雨式的头脑反思与洗礼。在“面积复习”这一课中，学生根据自己的整理，绘制出辐射图、括号图、树状图、鱼骨图等形式的思维导图（图2），图文并茂，条分缕析，真是可圈可点。从图中可以看出，有学生绘制思维导图的形式虽然不同，但都是殊途同归。这个时候，教师要安排一次交流，让其他学生指出思维导图的优缺点后，留出足够的时间让学生进行自我反思，寻找课前自己绘制的思维导图中的不足，做进一步的调整与修改。这样的复习课，有效进行了学科融合，在建构知识网络、形成知识体系的同时，锻炼了学生的口语交际能力，培养了他们欣赏美和表达美的情感。开放的课堂，趣味性强，既生动又活泼，学生乐在其中，复习的有效性不言而喻。

二、回归，夯实本质概念

学生已经基本弄清各知识点之间的内在联系，也已经明白复习课不仅是一个单元的整体复习，还是一个知识点的系统复习，也是相关联知识间的整合复习。学生经历了知识的聚合、思维的发散之后，更要关注知识点的巩固，让数学魅力得到充分发挥，以实现知识的本质回归。

（一）暴露缺陷，填补知识漏洞

课堂进入练习环节，目的是想通过适当的练习加强学生对知识的巩固。设计练习题时，教师既要考虑知识的广度和深度，也要考虑习题的梯度，让所有学生都能够暴露知识的缺陷，便于及时弥补知识漏洞。有这样三道题目：

1. 比较大小

7平方米○75平方分米

20000平方厘米○20平方米

3平方千米○3公顷

800米○800平方厘米

2. 用一张长2分米、宽18厘米的白纸，剪边长为3厘米的小正方形，最多能剪几个？

①36个   ②40个

③12个   ④120个

3. A、B两个花坛（图3），花坛中间有条石子路，这两个花坛的周长哪個长？

由于题目涉及的知识范围较广，思维含量较高，学生必须“用自己的头脑去分析”。习题的设计相对而言比较优秀，具有较高的层次性和启发性。课堂上，教师首先要求学生独立思考自主完成相应的练习，接着在全班范围内订正答案。学生自行订正后，暴露出本单元的知识掌握缺陷之处，便于接下来的条分缕析，加强针对性的练习，来填补这一知识的漏洞。

（二）条分缕析，提升思维品质

一节课最精彩的部分必定来源于学生。质疑提问、生生互动，这一条路必须坚持走下去，做到真正地把时间还给学生，把课堂还给学生。对于上文三道题目的训练所暴露出来的知识缺陷，笔者组织学生进行深入的探讨与分析，寻找错误原因并对症下药。第1题中学生暴露的主要问题是单位之间的换算是乘以进率还是除以进率弄不清，第4小题出现大于号也大有人在。这是把长度单位与面积单位混为一谈了。第2题则简单地认为20×18÷（3×3）=40（个），这种计算，从理论层面来讲，是完全正确的，殊不知实际裁剪时，长边只能剪6次，宽剪6次刚好，正确答案应该选①36个。错误原因是脱离了生活实际。第3题很多学生认为，A花坛的周长大于B花坛，只要动手用笔画一画，正确答案是显而易见的。两个图形的周长都是长加宽再加石子路的长度，是一样长的。错误原因还是没有把长方形周长和面积的概念弄清楚。学生明白，这个过程中，一定要用“表达”的方式发表自己对习题的审题与分析、解题的方法与思路、解题的过程与体会，不人云亦云，要能够“用自己的语言去支撑自己的分析”，并逐渐地树立起自主学习的意识和思维品质。

（三）综合运用， 获得知识技能

抽象的数学知识光靠口头描述，部分学生会难以接受，更难以进一步地深入和拓宽知识面。这里拓宽的不仅有学习技能的空间，还有实践运用的空间。为了更好地弥补知识的漏洞，夯实本质概念，教师要加强对这些知识的综合训练。

1. 仔细推敲，认真辨析。

（1）一个正方形，边长是4分米，它的周长与面积相等。（    ）

（2）面积相等的一个长方形和一个正方形，它们的周长一定相等。（   ）

2.小芳家准备将客厅地面铺上地板，有两种规格的地板可供选择，第一种长90厘米，宽10厘米，第二种长120厘米，宽20厘米，已知客厅长8米，宽4米5分米，请你帮忙算算各需多少块？

3. 第一个正方形的边长比第二个正方形的边长长3厘米，第一个正方形的面积比第二个正方形的面积大57平方厘米，求每个正方形的面积。

习题的设计相对而言比较优秀，针对性强，具有较高的层次性和启发性。第1题辨析，是针对学生把周长和面积概念混淆设计的；第2题是针对学生脱离生活实际设计的；第3题就是一道集综合性和挑战性于一体的题目，让学有余力的学生挑战一下。通过综合训练，学生在获得各种认知策略、发展反思、元认知等能力的同时，认知水平不断攀升，知识体系牢固建构，知识技能不断获得，解决问题也得心应手。

三、发散，展示数学魅力

在思维上，数学知识的整理与复习课的设计应该体现“发散”，把数学核心知识置于多维度的问题情境之中，并以其为中心进行拓展、发展，引导学生形成多角度的思维，并建立知识间的多元联系，做到形散神不散。常用的综合训练是对学生进行“发散”思维训练的重要形式。

（一）横向扩散，培养思维的广阔性

横向扩散就是指由一道题目横向发散出一类题目，粗看面目很相似，细细思考却别有洞天。学生通过学一道题，获得解一类题的本领，呈现“一把钥匙开多把锁”的大好局面，能帮助自己认清知识间的关系，培养思维的广阔性，加深对知识的理解。

用20厘米长的铁丝可以围成几种不同的长方形（长和宽均为整数），计算围成长方形的周长和面积，填入表2。然后观察表中的数据，说说你都知道了什么？

通过进行排列分析，可以得到五种情况，发现不管长与宽怎么变化，周长都不会改变，但随着长与宽的长度差距逐渐减少，面积则逐渐变大，正方形的面积比长方形的面积都大。由此横向扩散至“一张边长是10厘米的正方形纸中，沿边缘剪去一个长6厘米、宽4厘米的长方形。剩下部分的面积是多少？剩下部分的周长呢？”的剪纸问题和铺地板问题，都可以用这种排列的方法解决。运用排列的方法，可以训练学生思维的系统性，培养学生全盘考虑问题的能力。这样的训练越多，学生的思维就会变得越缜密，分析问题的能力也会不断提升，这对培养学生思维的广阔性大有裨益。

（二）逆向求异，培养思维的灵活性

逆向求异是指一道习题，由于不同学生所审视的方向各有不同，因此解题思路也就不同。这是一种训练力度较大的思维活动，开放的条件，开放的结论，必定通过开放的思维方式来解决问题。学生练了太多的顺向思维的习题，碰到逆向思维的习题就束手无策，显得思维的灵活性不够。求长方形的周长和面积，往往要先知道长方形的长和宽是多少，然后按照公式代入计算即可。这种顺向思维的问题是比较容易解决的。然而，有这样两道题目，如右上。

1. 在方格纸上画几个长方形或正方形，使它们的周长都相等，然后比较一下它们的面积，你能发现什么？

2. 画出面积是24平方厘米的长方形（长宽是整厘米数），并计算出这些长方形的周长。

这两道题目已知周长和面积，长与宽都是开放的，只有在厘清它们的内在联系后，方能理顺彼此的关系，找到科学的解决办法。在复习课习题教学中，教师要抓住一切有利时机，经常有意识地启发、引导学生在所学的知識范围内思考不同的解题思路，有利于培养学生思维的灵活性。

（三）纵向挖掘，培养思维的深刻性

纵向挖掘，就是由一道基础题，不断增加条件，习题的难度跟着一步步加大。对于这些纵向挖掘的习题而言，其复杂程度可想而知。这就需要教师对固有条件进行综合剖析，找准变量与不变的量，进行变式训练。

1. 学校操场原来长50米，宽20米，这个操场面积多少平方米？

2. 学校操场原来长50米，宽20米，扩建后长增加50米，这个操场面积增加多少平方米？

3. 学校操场原来长50米，宽20米，扩建后长增加50米，宽增加20米，这个操场面积增加多少平方米？

课堂上，学生读题后提问：这三道题，有什么不一样？通过读题，学生发现，第2题只有一个变量，第3题有两个变量。看得出来，由第1题演变出的2、3两题颇具挑战性。这类“变式”训练，极易激发学生参与挑战的欲望，让他们在比较中寻找解决问题的方法，在挑战中享受学习的乐趣。通过一题多探、一题深探的课堂实践，实现了真正意义上培养学生探究能力和实践创新能力以及思维的深刻性。

总而言之，巩固旧知，又获得新知，在不断循环的过程中，学生的认知水平得到螺旋上升。教学中，教师善于启发学生的多维思维进行整体复习，向学生渗透事物间互相联系、互相依存的辩证思想，不仅有利于加深对面积单元知识的巩固，还有利于培养学生有序思考、归纳整理的能力，推动学生在原有基础上进一步发展，在真实学习中进一步成长！