基于智慧课堂发展高中生数学直观想象素养的实践研究

摘 要：以高中生数学直观想象素养培养为切入点，利用智慧课堂平台实现信息技术和学科教学深度融合，结合发展学生直观想象素养的要求，设计相应教学范式，指导《圆锥曲线的光学性质及其应用》的教学实践.

关键词：智慧课堂；直观想象；教学范式；圆锥曲线；光学性质

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2022）30-0024-03

收稿日期：2022-07-25

作者简介：武四海（1986.9-），男，湖南省株洲人，本科，中学一级教师，从事高中数学教学研究.

基金项目：本文是课题《基于智慧课堂培养高中生数学直观想象的实践研究》（课题编号：GZSX2021004）阶段性研究成果.

随着中小学教育教学数字化转型，信息技术赋能教学作用凸显，智慧课堂应运而生，目前学术界还尚未形成对智慧课堂內涵的统一界定.通过查阅文献等资料，大部分研究者均认同智慧课堂不等同于智慧教室，需要以信息技术为载体，师生共同作用才能有效果.学生的全面发展才是创建智慧课堂的核心，课堂应以学生为学习主体，教师通过情境、问题导向的互动式、启发式、探究式、体验式等教学方式，引导学生深度体验、善于思考、严谨求实，全方位参与知识形成全过程，全面践行学科独特育人价值和发展素质教育.

学术界关于发展高中生数学直观想象素养的培养方面的研究，主要有宏观与微观两个层面的实践与研究.宏观层面是从教师的教、学生的学以及教材的处理等因素入手提出的培养策略，在宏观层面的研究中，直观想象素养的培养直观反映在学生作图、识图能力提升.如邬烈荣、毛敏君等人探讨在教学路径中培育学生的直观想象素养，提出以图形为入手点，通过“剖析章头图、驾驭直观图形、促生新思维生成”三策落实直观想象素养的培养，又如沈金兴、王奋平等人在分析Pierre Van Hiele的几何思维发展模型和Duvall的几何认知关系模型后，在数学教育心理学（PME）视角下提出教师从以下三方面来培养学生的直观想象素养：一是为学生提供恰当的先行组织者、二是激发学生的元认知监控和调节、三是设计适当的探究性问题，并从PME视角给出了具体的培养策略.微观层面是借助具体的媒介为载体，如几何图形、直观载体、想象素材等，在微观层面的研究中，直观想象素养的培养注重学生体验并理解知识的动态生成.

因此笔者认为，基于智慧课堂发展高中生数学直观想象素养的“智慧课堂”需要培养学生“做中学”、“悟中学”，可概括为方便操作的四个着力点：科学预设、体验生成、质疑分享、评价激励.

并初步探讨出培养高中生数学直观想象素养的智慧课堂教学范式流程图如图1.

根据如上研究出来的教学范式，设计《圆锥曲线的光学性质及其应用》的教学实践过程如下：

1 课前环节

1.1 任务发布：

教师课前根据教学内容，科学预设学习任务，通过智慧平台推送给学生.

我们知道，当一束光照到镜面时，光线会依一定的规律反射，即反射角等于入射角（如图示）.当光照射到曲面时，特别是由圆锥曲线绕其对称轴旋转而成的曲面时，会有什么现象呢？

请同学们自学2019新人教A版高中数学选择性必修第一册P140页阅读与思考《圆锥曲线的光学性质及其应用》，为检测课前预习的效果，探究如下任务.

任务 利用圆锥曲线可以实现将点光源（ ）（多选）

A.聚焦于另外一点 B.散射

C.转换成平行光源

1.2 素材收集：学生通过生活或网络收集素材，尝试完成预习任务.

预习任务：通过查阅资料，你还能找到生活中有那些有趣圆锥曲线光学性质应用？

2 课中环节

2.1 展示分享

学生在课堂上展现自己的任务完成情况，分享自己的思考，解决方式和疑难困惑.

2.1.1 椭圆的光学性质

文字语言：从椭圆的一个焦点发出的光线，经过椭圆的反射，反射光线交于另一个焦点；

2.1.2 双曲线的光学性质

文字语言：从双曲线的一个焦点发出的光线，经过双曲线的反射，反射光线是散开的，它们就好像是从另一个焦点射出的一样；

2.1.3 抛物线的光学性质

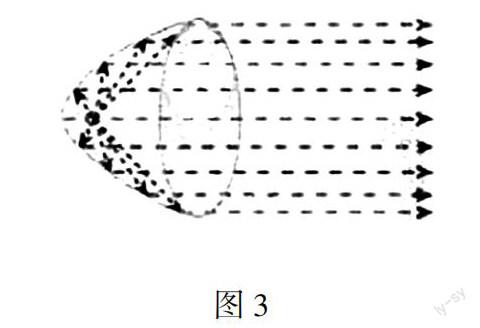
文字语言：从抛物线焦点发出的光线，经过抛物线上一点的反射后，反射光线平行于抛物线的对称轴.

2.2 情境创设与微课讲评

情境创设1：教师根据学生收集的素材，以及完成预习任务时遇到的问题，通过智慧教学平台创设情境，感受问题的生成.

情境创设2：我们在生活中的一个实例：一只很小的灯泡发出的光，会分散地射向各方，但把它装在圆柱形手电筒里，经过适当调节，就能射出一束比较强的平行光线，这是为什么呢？

微课教学：在学生体验到问题的生成后，教师在智慧教学平台播放事先制作好的微课教学视频等素材，让抽象的几何知识探究过程可视化；

微课讲评1：教师利用信息技术充分展示圆锥曲线光学性质的动图，学生通过直接观察，空间想象，尝试解决情境创设中的问题，提升学生直观想象素养；

微课讲评2：以椭圆的光学性质为例，可否将图4及其文字语言转换为与之相对应的数学符合语言呢？并证明之.

追问1：反射界面、法线在哪里？

追问2：如何证明F₁P，F₂P就是入射光线与反射光线呢？

例1 已知椭圆x²a²+y²b²=1（a>b>0），l为椭圆上一点P（x₀，y₀）处的切线，PA为过点P且垂直于l的法线，交x轴于点A，证∠F₁PA=∠F₂PA.

师生一同进行推理论证（过程略）.

2.3 任务更新

例2 （2010年安徽省高考文科数学第17题）椭圆E经过点A（2，3），对称轴为坐标轴，焦点x²16+y²12=1轴上，离心率x²16+y²12=1.

（1）求椭圆E的方程；

（2）求x²16+y²12=1的角平分线所在直线的方程.

（1）椭圆E的方程为x²16+y²12=1

（2）方法一（轨迹方程法）：

（3）由（1）知F₁（-2，0），F₂（2，0），所以直线AF₁的方程为

y=34（x+2），即3x-4y+6=0，

直线AF₂的方程为：x=2.

解析 由椭圆E的图形知，∠F₁AF₂的角平分线所在直线的斜率为正数，设P（x，y）为∠F₁AF₂的角平分线所在直线上任一点，则|3x-4y+6|5=|x-2|.

若3x-4y+6=5x-10，得x+2y-8=0，其斜率为负，不合题意，舍去.

于是3x-4y+6=-5x+10，即2x-y-1=0.

所以∠F₁AF₂的角平分线所在直线的方程为2x-y-1=0.

2.4 课中评价

（1）在例2的讲解时，教师一方面深化学生对椭圆的光学性质的理解与认识；另一方面对比两种解法，突出借助椭圆的光学几何性质优越性.

（2）教师发布巩固练习后，学生利用智慧教学平板提交自主探究的结果，平台迅速智能批改，并将批改结果及时反馈给教师和学生，教师根据评价结果，有选择的解析任务.

3 课后环节

3.1 个性化作业

智慧教学平台结合学生课中评价结果，智能推送个性化作业给教师和学生，教师可微调作业容量和难度.

3.2 智能评价

学生完成个性化作业后上交，智慧教学平台结合课中评价和课后作业，智能给予学生和教师评价反馈；教师根据智能评价充分了解学生情况，对个别学生进一步辅导.

参考文献：

[1]邬烈荣，毛敏君.例谈数学教学中学生“直观想象”能力的培养[J].教学月刊（中学版·教学参考），2017（Z2）：36-39.

[2] 沈金興，王奋平.从PME视角看直观想象素养及其培养[J].教育研究与评论（中学教育教学），2017（04）：11-15.

[3] 张教训，韩红军.在解题教学中培养学生直观想象素养的四个视角[J].中学数学，2019（01）：94-97.

[4] 张教训，韩红军.培养高一学生直观想象素养的途径[J].中学数学，2017（15）：31-34.

[5] 乔霁，高琳，庞之与，杨芳，陈莉.超级画板对学生直观想象能力的培养探究[J].贵州师范学院学报，2016，32（09）：68-72.

[责任编辑：李 璟]