基于学生数学素养发展的创新试题设计

钱春燕

［摘  要］ 适切地设计和改编创新试题不仅可以体现学科的宽度，还对培育创新意识和数学素养具有一定的导向作用。文章基于学生数学素养，针对封闭性数学试题进行改进，提出聚焦学生数学素养发展的创新试题改编路径：探究性创新试题——积累思维过程的智慧点；导向性创新试题——提升思维的参与度；过程性创新试题——孕育逻辑推理；层次性创新试题——强化综合应用能力。

［关键词］ 创新试题；数学素养；小学数学

数学教学不仅要关注知识技能，还应着眼于学生创新思维的培养。那么，如何开启学生的创造潜能，如何培养学生的创新意识，就成了教学改革的重要目标。小学阶段是学生创造性培育的初始阶段，创新试题具有挑战性，可以极大地激起小学生的好奇心。因此，适切地设计和改编创新试题不仅可以体现学科的宽度，还对培育创新意识和数学素养具有一定的导向作用［1］。如何设计创新试题？笔者依据教学内容和学生学情进行了一些有益的探索，与各位同行分享。

[?] 一、探究性创新试题——积累思维过程的智慧点

探究性问题可以激起学生认知心理上的冲突，让学生产生探究的心理状态，以寻求解题的各种方法策略，从而积累思维过程的智慧点。因此，教师应改习题为问题，努力设计好具有探究性的创新问题，试图开发学生思维潜能，帮助学生积累数学“原始”发现的经验，提高学生的探究能力和思维水平［2］。

例1  图1是几种不同规格的铁皮（有长方形和正方形两种）。

（1）利用6张规格①的铁皮，可以焊接出一个__________体油箱，该油箱的表面积是_____________，容积是__________。（焊接处忽略不计）

（2）若再利用规格②③④各两张去焊接一个长方体油箱，则该油箱的表面积是_________，容积是_________。（焊接处忽略不计）

原题分析：本题的两个小题都考查如何求立体图形的表面积和体积，此设计显然层次性不明顯，不具有探究性。因此，笔者对第（2）问进行了改造，将一个同一层次的“习题”转化为具有一定开放度和创造性的“问题”，让学生在探究和解决问题的过程中经历思维的流畅和发散训练。

改编后的第（2）问：倘若还需要焊接一个长方体的油箱，该如何选择铁皮？（请画出展开示意图，并写清楚选择的铁皮规格及张数）

方案1：______________________

方案2：______________________

方案3：______________________

点评：笔者在改造中将问题打开，给予学生更多的思考和想象的空间，鼓励学生大胆运用直觉和想象去猜测，运用各种途径去寻求任意可能的方案。在这个过程中，学生自然也能开动脑筋，还问题更多的惊喜，提出了许多巧妙的方案，使得本题的探究价值得到了进一步提升。

[?] 二、导向性创新试题——提升思维的参与度

一般情况下，试题过易，学生会深感索然无味；试题过难，学生又会产生畏难心理。基于此，教师在设计试题时，需要充分把握好问题的难易程度，对于一些难度过大的试题，可以将探究问题作为导向性指引，这样一来，才能给予学生思路上的指引，以提高学生思维的参与度。

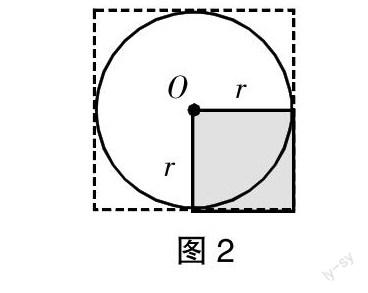
例2  如图2，小正方形的面积是10cm2，则圆的面积是_________。

原题分析：学生在解决本题时习惯性地去探求圆的半径，那么自然由于无法探求而思维受阻，此时，则易产生畏难情绪。为了让学生的思维更加顺畅，笔者对本题进行了以下改编。

（1）如图2，小正方形的面积是10平方厘米，即________。

（2）根据圆面积计算公式，若π≈3，据上述关系可求出圆的面积：S=_____。

（3）图2中的大正方形面积是___，根据这样的图形关系，若要在一张面积是60平方厘米的正方形纸上画出一个最大的圆，那么这个圆的面积是_____。（π≈3）

点评：为充分延展学生的思维，最大化地利用好本题的图像特色，笔者有意识地将本题进行了改造，改编后的问题更利于学生观察和思考，使学生通过探寻图形间的联系来完成问题的解析，促进创新思维的发展。

[?] 三、过程性创新试题——孕育逻辑推理

问题孕育创新，问题是创新之“始”，也是创新之“母”，教师在设计创新试题时不仅需要关注问题的导向性，还需关注过程性。因为，解决一道数学问题并非仅仅考查学生的解题思路与策略，在很大程度上也是对推理能力的考量。倘若教师在改编一些较为抽象难懂的试题时可以注意到过程的细化，则可引发学生的猜想，让学生进一步有序思考和分析问题，以实现对逻辑推理和分析能力的培育。

例3  红红和芳芳正在玩卡片游戏，每个人从2，4，5，7这4张卡片中任抽一张，若两数之积为偶数，则红红赢，反之芳芳赢。依照这样的玩法，则（    ）。

A. 芳芳赢的机会大

B. 红红赢的机会大

C. 两人赢的机会相同

原题分析：本例最显著的特点是抽象性大，大部分学生是直接判断赢的对象，那么思考过程就直接省略了，无法考查学生的思考过程。倘若这里能通过细化问题，让过程显性化，则可以达到训练逻辑推理能力的效果。为此，笔者进行了如下改编。

红红和芳芳正在玩卡片游戏，每个人从2，4，5，7这4张卡片中任抽一张，若两数之积为偶数，则红红赢，反之芳芳赢。

（1）随意抽出的卡片中，两个数的积有可能出现以下结果：2×4=8，______________________。（请写出可能出现的所有结果）

（2）按照这样的玩法，芳芳赢的可能性可以用分数______表示。

（3）按照这样的玩法，则（     ）。

A. 芳芳赢的机会大

B. 红红赢的机会大

C. 两人赢的机会相同

（4）在不改变游戏规则的情形下，将4张卡片中的数字_____换成____，这个游戏就公平了。

点评：问题在教师的改编下，有了有序思考的灵魂，有了透彻理解“可能性”和“游戏公平”的支柱，最重要的是改造后的问题开放性较强。此时，由于习题是开放的，学生的求解思路是延展的，有利于发散性思维的培养。

[?] 四、层次性创新试题——强化综合应用能力

每个学生都是独特的个体，尤其在知识、能力等因素上有很大的差异。传统试题不仅“题海无边”，更是形式单一，常常让一些学生在遇到稍有难度的试题时思维卡壳。事实上，人的经验反馈网络具有一定的层次性，作为一定经验基础上的习题设计也应具有相称的层次性。因此，教师应富有创造性地改编问题，让改编问题具有层次性和创造性，这样才能在深化知识理解的同时增强学生的综合应用能力。

例4  一辆巴士从A城开往B城，已经行驶了全程的3/10，此时距离B城还有84千米，试求出A城和B城的距离。

原题分析：显然，面对这样一道复杂的行程问题，一眼看不到解题的具体思路。而以解决问题为线索进行问题的改造，探寻深入追问的机会，则可以有效拓展学生的思维空间，让解题思路流畅而自然地显露出来。于是，笔者对原题进行了如下改编。

一辆巴士从A城开往B城，行驶了全程的3/10。

（1）试着在图3中用▲标注此时巴士行驶的位置：

（2）若此时巴士距离B城的距离是84千米，试求出A城和B城的距离。

（3）若此时巴士距离A、B两城的中点还有20千米，试求出A城和B城的距离。

（4）一直以这样的速度行驶下去，该巴士到达B城还需要多长时间？

（5）巴士的油箱原有78升汽油，此时剩下了54升，按照这样来算，剩余的汽油量能行驶至B城吗？

点评：所有的“教”都是为了“学”，改编问题的最终目标是让学生“学好”，故而要明确问题设计的“价值”追求，简而言之就是改编问题的目的所在。试题经笔者之手改编后由“知识立意”转变为“能力立意”，充分体现了“能力立意”的思想。事实上，这样的改编一方面降低了试题的难度，如第（1）（2）問虽为基础题，但指引学生借助数形结合进行思考也是其本质目的。之后的3个问题的难度逐步加深，并渗透了几分挑战性，让学有余力的学生可以充分体验探究和收获的喜悦，这种走向层次性的创新试题改编取向本身也是向学生传播创造性思维［3］。

总之，新课程理念下推崇创新意识和创造潜能，是值得教师倾听和思考的。教师唯有用发现的眼光进行试题设计，才能拓展学生的思维，让更多的学生爱思考、爱探究、爱学习，发展数学素养。想来，这种走向素养提升的创新试题改编也是值得教师继续努力的。

参考文献：

［1］  邱贞辉. 初中数学例题及习题教学设计研究［J］. 中学课程资源，2017（01）：26-27+34.

［2］  左俊凤. 充分利用教材培养学生的探究意识［J］. 中学数学，2003（02）：13.

［3］  雷淇未. 利用教材例题培养学生创造性思维［J］.中学数学月刊，1997（11）：10-11.