小学生数学基本活动经验的积累研究

[摘 要] 研究者以自身的具体教学实践为例,提出“适切的情境”“开放性的探究活动”和“具体的实际应用”三个积累数学基本活动经验的途径,确保学生在亲身经历中积累更多的直接经验、间接经验和思维经验,从而使学生的能力在经验的积淀中获得更多的提升。
[关键词] 数学基本活动经验;直接经验;间接经验;思维经验
传统课堂教学中,教师好似演员,整节课不停地表演,使得讲解和分析占据整个课堂;而学生好似观众,只需“静坐观课”,很少主动参与知识的探究与学习。在这样的教学模式下,学生只能掌握数学知识的“皮毛”,无法真正领悟知识的内涵与外延,更不要说灵活运用知识了。
新课程强调的是学习方式的变革,倡导学习主体的转变,给予学生足够的时空思考数学问题,研究数学逻辑,探索数学奥秘,交流数学应用,如此灵动的数学课堂,需要学生具有一定的“经验”。因此,教师应设计适切的教学活动,让学生亲历操作、思考和探究,实现从感性认识到理性认识的飞跃,使得活动经验的内涵越发丰富,从而积累充足而有效的活动经验。下面笔者以自己的具体教学实践为例,从多个角度着手谈谈在教学中积累基本活动经验的教学思路。
一、依托适切的情境,积淀直接经验
1. 游戏情境
喜欢游戏是儿童的天性,教师设计数学活动可以将游戏融入其中,为数学知识增添活力,为数学课堂增添生机,这样则可激发小学生的学习兴趣,使其兴致勃勃地参与活动,获得直观体验,自主地吸收活动经验,有效地积淀直接经验。
案例1 立体图形的认识
游戏情境:找朋友
(1)请带着长方体、正方体、圆柱、球的4名学生先到讲台上来。
(2)请大家带着你带来的生活用品依次到讲台上来“找朋友”。
(3)请找到朋友的学生说一说,为什么你们是“朋友”。
(4)摸一摸你的“朋友”,并说一说它们有何特征。
设计意图:通过“找朋友”的游戏情境进行切入,使得枯燥的数学知识变得生动,使得数学概念融于学生喜闻乐见的游戏中,丰富他们的内心体验,让学生用多感官去感知各种立体图形的形状特征,从而探寻到立体图形的本质,自然地积淀直接经验。
2. 操作情境
活動经验的积淀与数学知识的学习密不可分,而积累活动经验必须让多感官参与其中,学生在手、口、脑的参与下才能丰富操作经验。基于此,教师应提供丰富的素材去设计和构造操作活动,帮助学生积淀直接经验。
案例2 分数的初步认识
活动1:取出准备好的长方形纸片,通过折和涂,表示出它的1/2。
要求:同桌两人一组应生成不同的折法,并交流“它的1/2是如何得到的”。(学生积极投入操作,直观感受1/2,同桌两人交流折法,并在思考与交流后有了一定的认识)
活动2:是否还存在其他不同的表示方法?(为了让学生叠加体验,又一次开展了更加深入的操作活动)
活动3:试着通过折和涂,表示出长方形、圆形和等边三角形的1/2。(以问题引导学生继续折和画,以外显的行为操作,深化学生对分数本质的理解)
设计意图:以操作情境为指引,在轻松愉悦的课堂氛围中让学生自主探究和合作交流,进一步明晰“分数的本质属性是无论图形如何变化,只需将其平均分成2份,其中的任意一份就是它的1/2”。这样的活动过程耗时不多,但学生在动手、动脑和动口中愉快体验,获得了更加形象的分数概念,并为进一步探索1/4、1/8等分数的本质特征奠定了操作基础,积淀了直接经验。
二、依托开放性的探究活动,积累间接经验
间接经验的获取直接指向问题的解决,它需要的是一种开放的、创造性的活动,让学生在活动中有经历、有体验、有数学思考,这样才能实现对经验的获取与积累。因此,教师应时常抛出特定情境下的特定问题,组织适度的开放性的探究活动,激发学生的探究意识,让学生进行外显的行为操作与思维层面的操作活动,积累充分而有效的间接经验。
案例3 三角形三边的关系
活动1:试着用3根小棒围出一个三角形,并思考任意的三根小棒都可以吗?
活动2:用四组长度不同的小棒验证刚才的猜想,并说一说你的发现。(学生经过探究与交流,很快有了新的发现)
活动3:是否只需要两根小棒的长度之和大于另一根小棒,就能围成三角形呢?请再一次通过操作进行验证。
设计意图:整个探究活动的设计环环相扣,为学生的主动探究搭起了桥梁,不断促进思考的深入。此时的操作与探究成了学生自主的需求,由于学生对探索的结果充满渴望,因此在探究活动中,学生所积累的经验也会因个体的强烈感知而更具有生命活力。就这样,既有独立思考的成分,又有合作学习的融入,新知在操作中变得清晰,在数学思考中逐步深入,逐渐形成间接经验。
三、依托具体的实际应用,增强思维经验
思维经验的积累是伴随着思维活动的过程而产生的,但这样的认知体验是碎片式的,也是不稳定的。因此,教师需要在教学中有意识地固化学生的认知体验,让学生最终形成根深蒂固的思维经验。依托具体的实际应用可以帮助学生构建“思维链”,这对于思维经验的积累十分有益。在问题解决的过程中激活已有的“思维经验”,在反思活动中进行经验的整合,并逐步形成新的“思维经验”,进而增强思维经验。
案例4 找规律
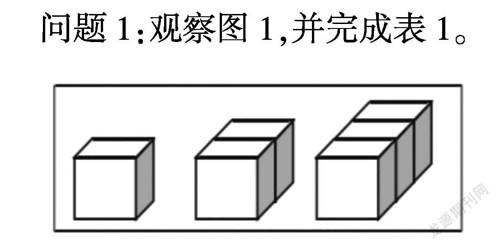
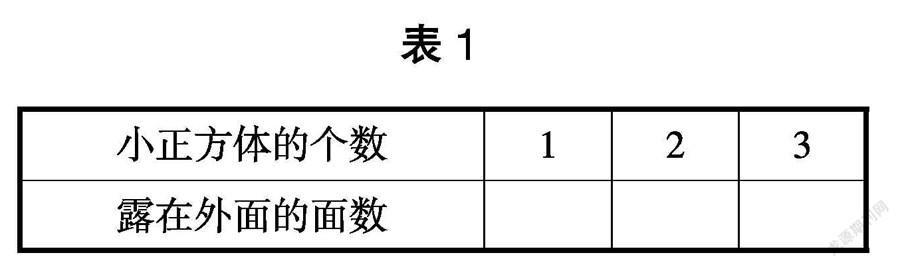
问题1:观察图1,并完成表1。
(在直接经验的影响下,学生借助图形轻松且快速地完成了表格的填写。)
问题2:结合问题1的图示与表格,继续完成表2。
(在直接经验的基础之上,融合间接经验,学生完成了表2的填写)
问题3:当小正方体的个数逐步增加到n个时,露在外面的面数又会是多少?
(此问题虽难度较大,但学生也能从直接经验与间接经验中找到方法,教师抛出这一问题后应大胆放手,让学生进行深层次的思考。学生深入观察图1,在经历思考、探究、讨论、思辨后可以得出“图1中的三个图的前后面露在外面的面数都是1;除去这两个面,每个小正方体的上面、左面和右面也露在外面”,进而得出:1个小正方体露出的面数是3×1+2,2个小正方体露出的面数是3×2+2,3个小正方体露出的面数是3×3+2”。以此类推,可以得出n个小正方体露出的面数是3×n+2。)
设计意图:为了解决找规律问题,教师采用了层层递进的思路,帮助学生感受规律,化解对这类问题的疑虑,实现让学生掌握解决这类问题的方法的教学目标。本设计旨在引导学生经历问题探究从低维到高维的升级过程,让学生产生拓展思维空间的主观愿望,在轻松愉悦的小组合作学习中找寻规律,从而获得对规律问题的全新理解,积累解决问题的方法,发展抽象思维能力。
总之,数学活动经验的积累需要教师在日常教学中一以贯之地提供“源泉”。从适切的情境的创设、开放性的探究活动和具体的实际应用的设计着手,基于教学内容与学生实际,促使学生产生思维的碰撞,让学生在亲身经历中积累更多的直接经验、间接经验和思维经验,使学生的能力在经验的积淀中获得更大的提升。
作者简介:王静(1993—),教育学硕士,小学二级教师,从事小学数学教学工作,曾获江苏省教师现代教育技术应用作品大赛二等奖、江苏省蓝天杯教学设计二等奖。

