板块模型高考真题回顾与拓展

程会琴　张金龙

板块模型是高中物理的经典模型之一，它能够将物体的受力分析、运动过程分析、力与运动的关系及相关的运动图象等力学主干知识串起来进行考查，因而备受高考命题专家的青睐。本文以2021年全国高考乙卷第21题为例引入，总结分析板块模型中的情境并进行拓展，旨在引导学生分析、归纳、总结板块模型的特点及相应的分析方法。

一、高考真题回顾

（2021年全国乙卷第21题）水平地面上有一质量为m1的长木板，木板的左端上有一质量为m2的物块，如图1所示。用水平向右的拉力F作用在物块上，F随时间t的变化关系如图2所示，其中F1、F2分别为t1、t2时刻F的大小。木板的加速度a1随时间t的变化关系如图3所示。已知木板与地面间的动摩擦因数为μ1，物块与木板间的动摩擦因数为μ2。假设最大静摩擦力均与相应的滑动摩擦力相等，重力加速度大小为g。则（ ）

【解析】由图3可知，t1时物块与木板一起刚开始滑动，此时物块与木板相对静止，以整体为研究对象有F1=μ1（m1+m2）g，故A错误。由图3可知，t2时物块与木板刚要发生相对滑动，以整体为研究对象，根据牛顿第二定律，有F2-μ1（m1+m2）g=（m1+m2）a;以木板为研究对象，根据牛顿第二定律，有μ2m2g-μ1（m1+m2）g=m1a>0，解得F2=（μ2-μ1）g，μ2> μ1，故BC正确。由图3可知，0～t2这段时间物块与木板相对静止，所以有相同的加速度，故D正确。

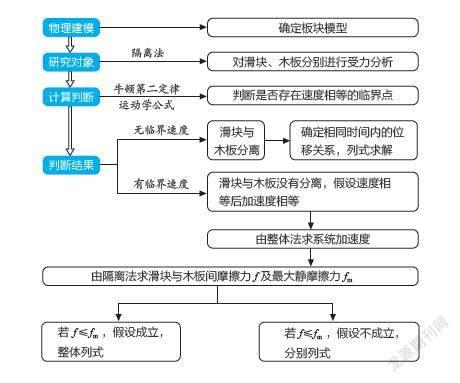
二、板块模型分析的思路总结

三、拓展训练

【情境1】地面和木板均粗糙，物块与木板均不受外力作用。设木板足够长，取v1为正方向，m和M同向运动。

（1） v1>v2时，对物块m，由μ1mg=ma1得知物块以a1= μ1g做匀减速直线运动;对木板M，由μ1mg-μ2（m+M）g= Ma2得知木板以a2= 做匀加速直线运动。

（2） v1

共速后，对于物块，最大加速度am=μ1g，需要考虑物块和木板是否会出现相对运动，先假设无相对滑动，二者加速度相同，对整体有μ2（m+M）g=（m+M）a，a=μ2g。若a≤am，即μ1≤μ2时，二者以共同的加速度a=μ2g做匀减速直线运动;若a>am，即μ1>μ2时，物块以较小的加速度a1=μ1g做匀减速直线运动，而由μ2（m+M）g-μ1mg=Ma2得知，木板以a2= 做匀减速直线运动，不可能出现与物块同步运动的情况。

【例1】如图5，一长木板在水平地面上运动，在某时刻（t=0）将一物块轻放到木板上，已知物块与木板的质量相等，物块与木板间及木板与地面间均有摩擦，物块与木板间的最大静摩擦力等于滑动摩擦力，且物块始终在木板上。在物块放到木板上之后，木板运动的速度-时间图象可能是下列选项中的（ ）

【解析】设在木板与物块未达到相同速度之前，木板的加速度为a1，物块与木板间的动摩擦因数为μ1，木板与地面间的动摩擦因数为μ2。对木板应用牛顿第二定律得-μ1mg-μ2·2mg=ma1，解得a1=-（μ1+2μ2）g。设物块与木板达到相同速度之后，木板的加速度为a2，对整体有-μ2·2mg=2ma2，a2=-μ2g，可知|a1|>|a2|，由v-t图象的斜率表示加速度大小可知A正确。

【情境2】地面与木板均粗糙，物块受外力F作用，物块初速度小于木板速度。设木板足够长，取v1为正方向，m和M开始时运动方向相同，且v1μ1mg>μ2（m+M）g时，物块速度反超木板;当F>μ1mg，μ1mg<μ2（m+M）g时，物块做匀加速直线运动，木板做匀减速直线运动;当F<μ1mg，μ1mg<μ2（m+M）g时，物块与木板均做匀减速直线运动。

【例2】在光滑水平面上有一质量为m1的足够长的木板，其上叠放一质量为m2的木块。假定木块和木板之间的最大静摩擦力和滑动摩擦力相等。现给木块施加一随时间t增大的水平力F=kt（k是常数），木板和木块加速度的大小分别为a1和a2，下列反映a1和a2变化的图象中正确的是（ ）

【解析】木块和木板之间相对静止时，所受的摩擦力均为静摩擦力，在达到最大静摩擦力前，木块和木板以相同加速度运动，根据牛顿第二定律知a= ;木块和木板相对运动时，a1=恒定不变，a2=-μg，a2是t的线性函数，t增大，a2也增大。由于< ，则木块与木板相对滑动后a2图象斜率大于a1图象斜率，故A正确。

【情境3】地面和木板粗糙，木板受外力F作用，物块初速度小于木板初速度。物块与木板共速前，对于物块m有μ1mg=ma1，物块以加速度a1=μ1g做匀加速直线运动;对于木板M有F-μ2（m+M）g- μ1mg=Ma2，加速度a2=。当a2=0时，F=μ2（m+M）g+μ1mg，物块以加速度a1做匀加速直线运动，木板做匀速直线运动，物块与木板可共速;当a2>0时，F>μ2（m+M）g+μ1mg，物块和木板均做匀加速直线运动，而木板加速度a2=≥a1时，即当F≥（μ1+μ2）（m+M）g时物块与木板不可能共速;当a2

【例3】如图8，一长L=2m、质量M=4kg的薄木板（厚度不计）静止在粗糙的水平台面上，其右端距平台边缘l=5m，木板的正中央放有一质量为m=1 kg的小物块（可视为质点）。已知木板与水平台面、物块与木板间的动摩擦因数均为μ1=0.4，现对木板施加一水平向右的恒力F，其大小为48N，g取10m/s2，求：

（1）F作用了1.2s时，木板的右端离平台边缘的距离;

（2）要使物块最终不能从平台上滑出去，则物块与平台间的动摩擦因数μ2应满足的条件。

【解析】（1）假设开始时物块与木板会相对滑动，由牛顿第二定律，对木板有F-μ1（M+m）g-μ1mg=Ma1，解得a1=6m/s2;对物块有μ1mg=ma2，解得a2=4m/s2。因为a2

设F作用时间t后，物块恰好从木板左端滑离，则有=a1t2-a2t2，代入数据解得t=1 s（另一解不符合题意，舍去）。在此过程中，木板的位移为x1=a1t2=×6×12 m=3 m，末速度为v1=a1t=6×1 m/s=6 m/s;物块的位移为x2=a2t2= × 4×12 m=2 m，末速度为v2=a2t=4×1 m/s=4 m/s。

在物块从木板上滑落后的t0=0.2 s内，由牛顿第二定律，对木板有F-μ1mg=ma2′，解得a2′=8 m/s2，木板发生的位移为x1′=v1t0+a1′t02，解得x1′=1.36 m。此时木板右端距平台边缘的距离为Δx=l-x1-x1′=（5-3-1.36） m=0.64 m。

（2）物块滑至平台后，做匀减速直线运动，由牛顿第二定律可知，对物块有μ2mg=ma2′，解得a2′=μ2g。若物块在平台上速度减为零，则通过的位移为x2′=，要使物块最终不会从平台上掉下去需满足l+≥x2+x2′，联立解得μ2≥0.2。