反应性双射流中标量输运和化学反应特性
李岩,田阿慧,周毅
(南京理工大学能源与动力工程学院,江苏南京 210094)
引 言
双射流和多束射流广泛存在于工业领域,如锅炉燃烧器、排气烟囱、发动机燃烧室等。双射流作为多束射流研究的基础模型是众多学者的研究对象。与均匀各向同性湍流相比,双射流的时空演化机理更为复杂,涉及诸多湍流过程(界面层卷吸、噪声的产生、射流拟序结构演化以及射流模态等)[1]。双射流流动往往伴随着化学反应,流动过程影响着标量的输运,而化学反应则决定了标量的产生及耗散。故研究双射流间相互作用和双射流间化学反应中的标量特性具有重要意义。
目前国内外学者在双射流流场统计特性[2-4]和射流间相互作用[4-7]等领域开展了一系列实验和数值模拟研究。在实验方面,Miller 等[6]、Tanaka[7]开展了关于双射流流场特性的开创性研究,将双射流流场结构分为收敛区、混合区和合并区三个区域。此后,学者多分析不同射流口间距[2-5]和不同射流口形状[4,8]对流场混合点位置、合并点位置和射流宽度的影响以探究双射流间相互作用。刘鹏远等[4]利用粒子图像测速技术(particle image velocity, PIV) 实验获得双射流速度场和湍流强度的分布,研究了高雷诺数下不同射流口间距对平行射流合并点位置的影响。Tanaka[7]对不同射流口间距的双射流流场开展了实验研究,分析了射流口间距对合并点后射流宽度的影响。与此同时,前人也利用数值模拟方法来研究流场特性,Mondal 等[9]对二维双射流进行了数值模拟,指出混合点位置与射流口间距存在线性关系。Li 等[10]在对双圆柱射流的大涡模拟数值研究中指出射流口间距和混合点之间存在指数对应关系。Zhou 等[5]根据直接数值模拟结果提出了双射流中射流流场相互作用尺度(jet-interaction length scale),指出该尺度可以预测双射流流场特性并根据该尺度解释了射流口间距与混合点位置的线性关系。
除流动空间演化特性相关研究外,工业中所遇到的射流问题往往涉及两个或更多不同组分标量的扩散、混合和化学反应,对此部分研究人员进行了相关实验研究[11-14]和数值模拟[15-18],旨在预测相关过程中混合速率以及控制化学反应速率。Stapountzis 等[11]采用化学敏感激光诱导荧光技术(laser-induced fluorescence, LIF)研究了反应性双平面射流,指出标量混合程度取决于射流口间距和射流轴向位置且流向最大平均浓度位置按照幂律增长。Soltys 等[12]使用双通道平面激光诱导荧光(planar laser-induced fluorescence, PLIF)系统量化了双圆孔射流从发射到合并过程中两个独立标量的瞬时协方差空间结构,研究了标量协方差空间结构对混合过程以及化学反应的影响。Watanabe等[13]基于光吸收光谱法浓度测量系统实验研究了反应性平面液体射流,结果表明反应物的浓度相关性越大平均反应速率越小。Cai 等[14]采用平面激光诱导荧光法和瑞利散射法实验研究了湍流同轴射流中的三标量混合,利用标量平均值、方差、相关系数、联合概率密度分布(joint probability distribution function, JPDF)等详细分析了近场流动中的混合过程,为理解和模拟反应流中的多尺度混合提供了基础。就湍流化学反应的数值模拟而言,考虑复杂详细机理会导致控制方程庞大,故用单步反应来简化详细化学反应机理以降低求解难度[19-20]。早在1962 年,Toor[21]进行了化学反应简化机理的研究,将传质-反应方程组简化为无反应传质方程并分析了具有等扩散系数的低浓度物质间快速均匀不可逆反应的传质过程。Bilger[22]针对非预混射流火焰发展了流体混合和化学反应的理论,用一个守恒的标量来充分描述混合,导出了任意组分的瞬时反应速率的表达式。但目前关于反应性双射流的数值模拟研究很少,仅有部分关于反应性单射流的相关模拟。DesJardin 等[15]对非预混反应单射流进行了大涡模拟,评估了几种亚格子模型的优缺点。Watanabe 等[16-18]对具有二级等温化学反应(A+BP)的平面单射流进行了系列数值模拟,分析了近场湍流/非湍流界面层附近的标量特性。
据文献统计,前人关于反应性双射流的研究大都基于实验分析,缺乏对反应性双射流中射流相互作用和组分相互作用影响机理的认识,亟待开展双平行射流标量输运和化学反应特性的数值模拟研究。本文对分别包含两种反应物的双射流之间的二级非平衡基元反应(A+BR)进行数值模拟,探究射流相互作用尺度在双平行反应性射流标量场的适用性,研究化学反应方程非稳态项、对流项、扩散项和化学反应源项对标量生成、消耗和输运的影响,旨在为射流混合及化学反应等领域的优化设计提供指导。
1 数值方法
1.1 流场计算
研究基于OpenFOAM 中pimpleFoam 求解器中结合非迭代瞬态PISO算法的PIMPLE算法。采用大涡模拟方法,滤波后的不可压缩流动控制方程组表达如下:

1.2 标量场计算
数值模拟使用类似于对动量方程的处理方式对化学反应控制标量输运方程进行求解。滤波后的化学反应控制标量输运方程表达如下:

式中,k为该二级反应的反应速率常数。
1.3 计算模型和参数
研究具体考虑分别含有不同反应物的两股射流之间的化学反应,不考虑射流与环境流的反应。图1 为化学反应流场和坐标系的示意图。反应物A和B 分别预先混合到射流Ⅰ和Ⅱ中。射流Ⅰ、Ⅱ通过宽度为d、射流口间距为Ld的两个狭缝喷射到环境流中。反应物A和B随着双射流在收敛区以对流和扩散的方式向周围环境及下游输运,在中心线附近反应物相互接触产生二级非平衡基元反应A+BR。
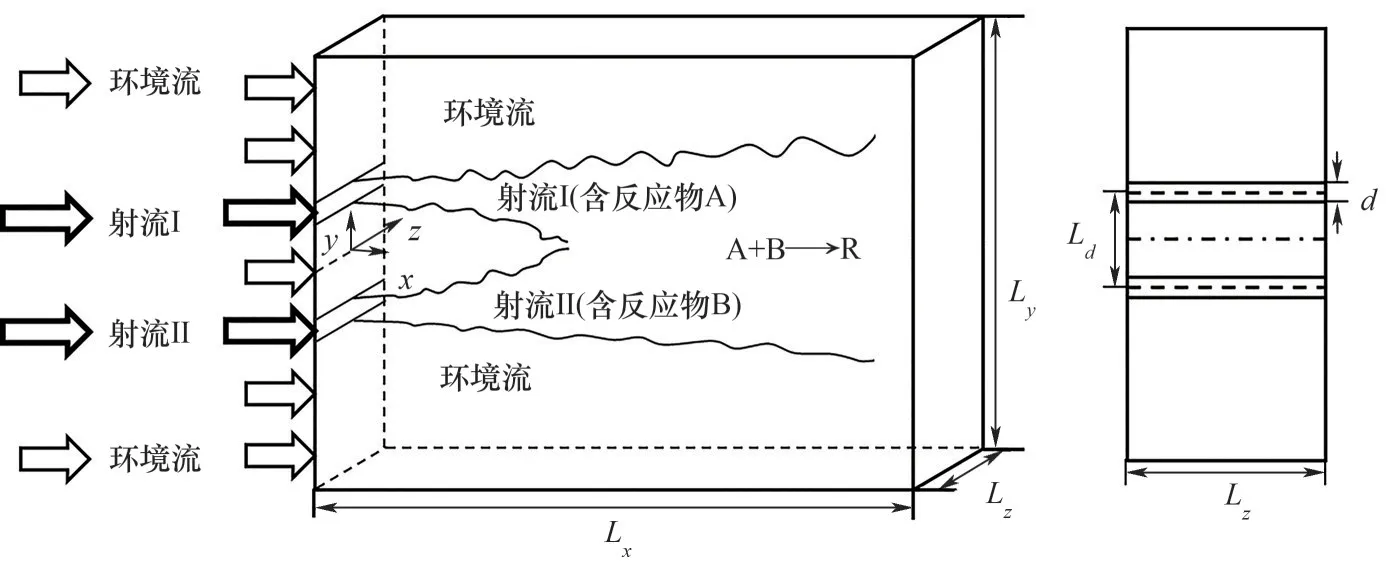
图1 数值模拟示意图Fig.1 Schematic diagram of the simulation
本文对不同射流口间距的三个双射流工况进行模拟,以探究射流口间距对流动-化学反应耦合过程的影响。表1为具体的计算参数及流场网格节点设置,Run J4、Run J6和Run J8分别对应射流口间距Ld/d=4, 6 和8。其中,雷诺数基于射流口平均流向速度UJ和射流口宽度d,Red=UJd/ν。UA为环境流速度,ΓA0和ΓB0分别为反应物A 和反应物B 的初始浓度。Damköhler 数(Da)是表示流动时间尺度和化学反应时间尺度之比的无量纲数,本文中其值由Da=k(ΓA0+ΓB0)d/UJ定义。设置计算条件如下:对于流场,射流口设置两个相等的平均流向速度UJ=UJetⅠ=UJetⅡ。为使双射流模拟尽快达到湍流状态,采用白噪声脉动法(“white noise”fluctuations)[23]在两个射流口处x,y和z方向添加速度脉动。本文中两个射流口处三个方向上添加的速度脉动均服从(-0.05, 0.05)均匀分布,其均方根值为Urms=Vrms=Wrms=0.029,该值小于Watanabe 等[18]研究中的射流口速度脉动均方根值最大值0.1,满足白噪声脉动法添加速度脉动的原则,即该值既能触发层流向湍流转换,又能保证其对流场统计结果影响不大。为降低环境流速度对射流运动的影响,研究采用与Zhou等[5]和Stanley 等[24]直接数值模拟中相同的环境流速度(UA/UJ=0.1)。流向出口采用对流流出边界条件,法向边界采用自由滑移边界条件,展向边界采用周期性边界条件。对于组分浓度场,设置初始浓度比ΓA0/ΓB0=2,产物初始浓度为0。设置施密特数Sc=0.71。采用OpenFOAM 中时间离散和空间离散格式。其中,时间递进采用二阶隐式backward,流场对流格式采用Gauss linear,标量场对流格式采用Gauss limitedLinear,扩散格式采用Gauss linear corrected,化学反应源项采用自动显式隐式fvm::SuSp。为节省计算资源同时精确捕捉双射流法向流场及标量场特性,在双射流法向发展范围即y方向(-10,10)范围内采用加密网格。
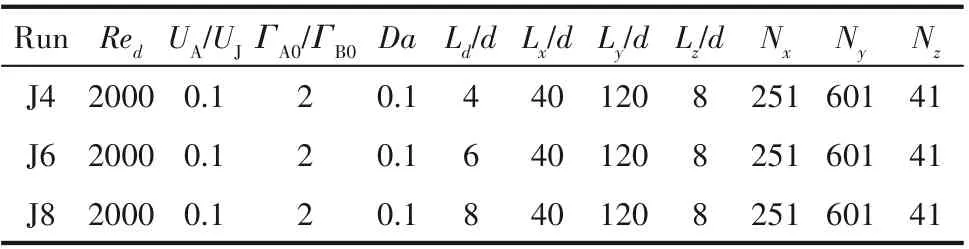
表1 反应性双射流计算参数及节点设置Table 1 Simulation parameters and node settings of reactive dual jets
2 数值方法验证
截至目前,国内外学术界尚未有关于两股射流之间化学反应的数值模拟或实验研究,无法直接验证数值方法的准确性。单射流和双射流同属于自由剪切射流且均存在湍流/非湍流界面,有类似的标量输运和化学反应特性,本文认为进行反应性单射流算例模拟并将模拟结果与前人研究结果进行对比同样能够证明当前数值方法的准确性。单射流算例中携带反应物A 的射流通过宽度为d的射流口射入到包含反应物B 的环境流中,随着流场发展单射流与环境流发生化学反应,计算条件设置与双射流算例相同。
图2为单射流算例无量纲平均流向速度的法向分布及其与前人的实验结果[25-26]和数值模拟结果[17]对比。其中,符号“〈〉”表示对时间以及z方向平均,UC为射流中心线上平均速度,bU为基于流向速度U的射流半宽,图中的Zone-averaged 表示达到自相似后对空间平均(z方向平均、x方向平均或y方向折叠平均)。当前流场在下游x/d=20 和x/d=30 处达到自相似,且与前人实验结果[25-26]和数值模拟结果[17]一致。图3 为无量纲速度脉动均方根值的法向分布,由于速度脉动均方根法向分布受初始场影响很大,前人实验结果[25-27]和数值模拟结果[24,28-30]中速度脉动均方根法向分布在一定范围变化,而当前模拟结果在该范围内表现出良好一致性。流向速度和速度脉动均方根的法向分布均与前人结果达到良好吻合,验证了流场模拟的准确性。
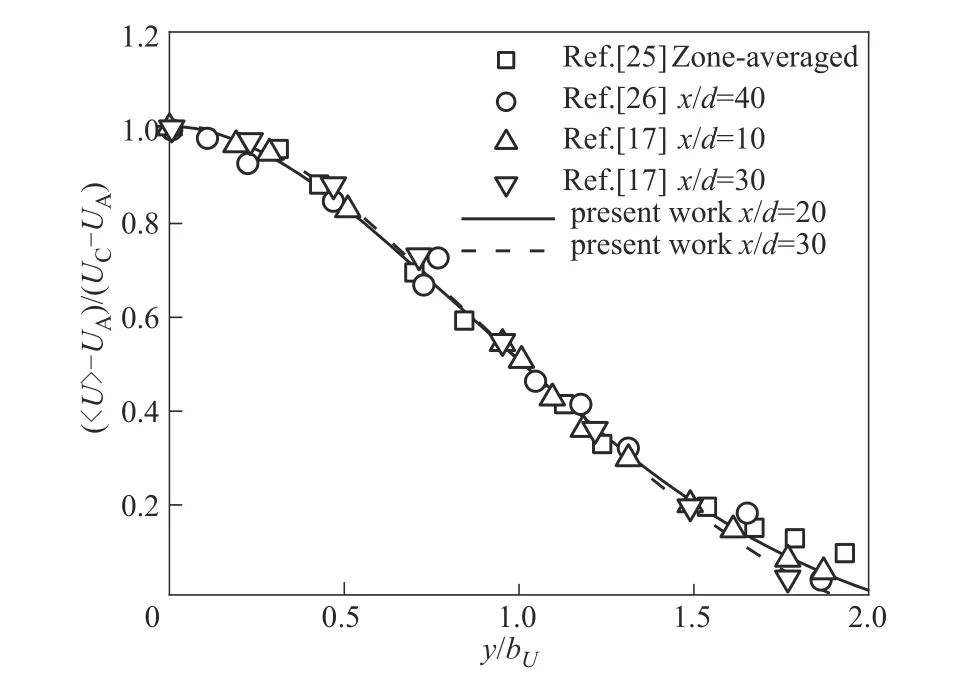
图2 单束反应射流无量纲平均流向速度法向分布Fig.2 Vertical distribution of normalized mean streamwise velocity of a reactive jet

图3 单束反应射流无量纲速度脉动均方根法向分布Fig.3 Vertical distribution of normalized turbulence rms value of a reactive jet
为了进一步验证化学反应模拟的准确性,验证混合浓度分数ξ的标量统计,ξ由式(6)给出:
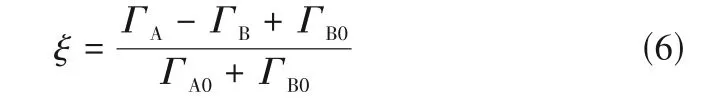
在相关数值计算中ξ可以提高化学反应与组分混合的计算效率。反应物A 和B的瞬时浓度可以由混合浓度分数和产物浓度表达如下:
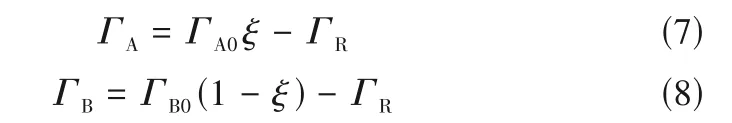
图4(a)为无量纲平均混合浓度分数ξ的法向分布。ξ以射流中心线上的平均混合浓度分数〈ξ〉C无量纲,法向坐标y以基于ξ的射流半宽bξ无量纲。混合浓度分数在下游达到自相似且与Watanabe 等[18]的结果吻合。图4(b)为混合浓度分数脉动均方根的法向分布。混合浓度分数脉动均方根与Watanabe等[18]数值模拟结果略有偏差,这一偏差是由验证算例所加射流口初始速度脉动强度与Watanabe 等[18]数值模拟所加速度脉动强度不同造成的。由此可见,当前标量场也与前人结果吻合较好,验证了化学反应模拟的准确性。
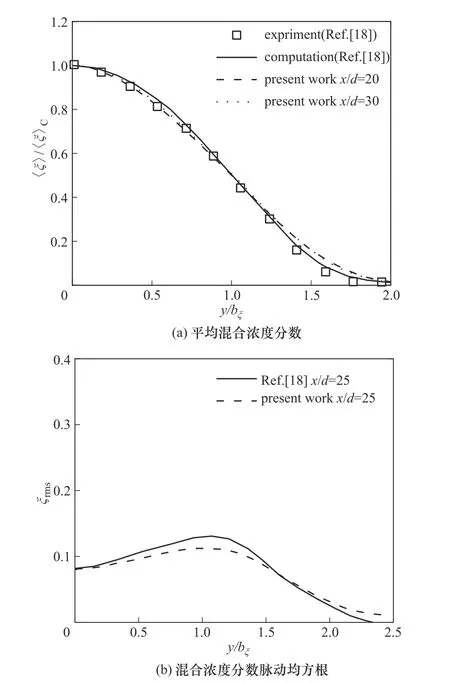
图4 单束反应射流无量纲平均混合浓度分数和混合浓度分数脉动均方根法向分布Fig.4 Vertical distribution of mean mixture fraction and mixture fraction fluctuation rms of a reactive jet
3 结果分析与讨论
3.1 流场和标量场可视化
研究人员根据混合点和合并点的位置将双射流流场结构分为收敛区、混合区和合并区三个区域[6-7],图5为典型的双射流流场结构图。其中,流场中回流出现且流向速度为零的点为准滞止点xqsp,回流消失且流向速度为零的点为混合点xmp,流场中心线流向平均速度最大的点为合并点xcp。收敛区指混合点之前的区域,该区域内射流对环境流的卷吸作用会使两股射流间形成低压区。混合区指混合点与合并点之间的区域。两股射流激烈碰撞剧烈混合会形成高压区。由高压区和低压区综合作用会导致在混合点前形成回流区。合并区指合并点之后的区域,合并区内两股射流完全合并为单射流并呈一定单射流特性[31]。
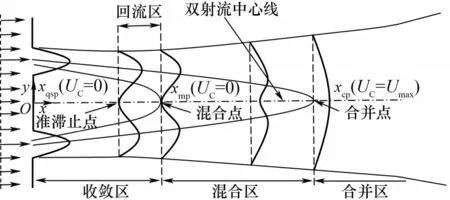
图5 双射流流场结构图Fig.5 Structure diagram of dual jet flow field
双射流中心线上两股射流间相互作用以及化学反应最为剧烈,中心线上的统计特性能直观地反映射流相互作用和组分相互作用对双射流流动和化学反应耦合过程的影响,因此下文考察双射流沿中心线上的流场统计量和标量场统计量的流向演化。图6为三种射流口间距下中心线上平均流向速度流向演化。随着流场的发展平均流向速度均有先减小后增大的趋势,并在上游都有负值出现,这说明在三种不同射流口间距的情况下,均会出现回流现象。表2 给出图6 三种射流口间距下准滞止点位置xqsp、混合点位置xmp和合并点位置xcp,可以看出准滞止点位置xqsp、混合点位置xmp和合并点位置xcp都随着射流口间距的增大而增大,且呈一定线性规律。
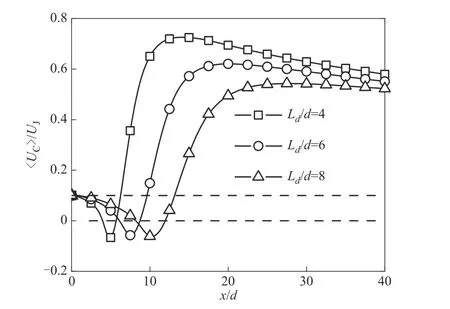
图6 中心线上平均流向速度流向演化Fig.6 Streamwise evolution of the mean streamwise velocity along the center line
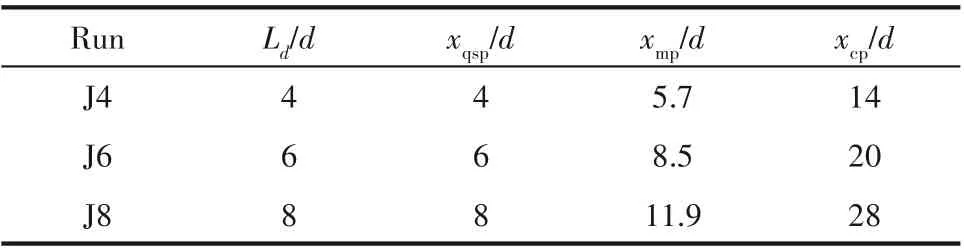
表2 三种射流口间距下准滞止点位置xqsp、混合点位置xmp和合并点位置xcpTable 2 The quasi stagnation point xqsp,locations of the merge point xmp,and the combine point xcp in the three cases of different jet separation distances
图7(a)为算例Run J4、Run J6 和Run J8 的中心线上流向速度脉动均方根的流向演化,流向速度脉动均方根在混合区内均有一个峰值,该点的射流相互作用极强。图7(b)为三种射流口间距下平均压力的流向演化。整个回流区均为负压,前人的研究中指出该负压是由中心线上的湍流/非湍流界面和被包围的非湍流区域之间的卷吸作用引起的[6-7]。同时,在回流区后存在一个高压区,其是由两股射流在混合点碰撞冲击引起的。
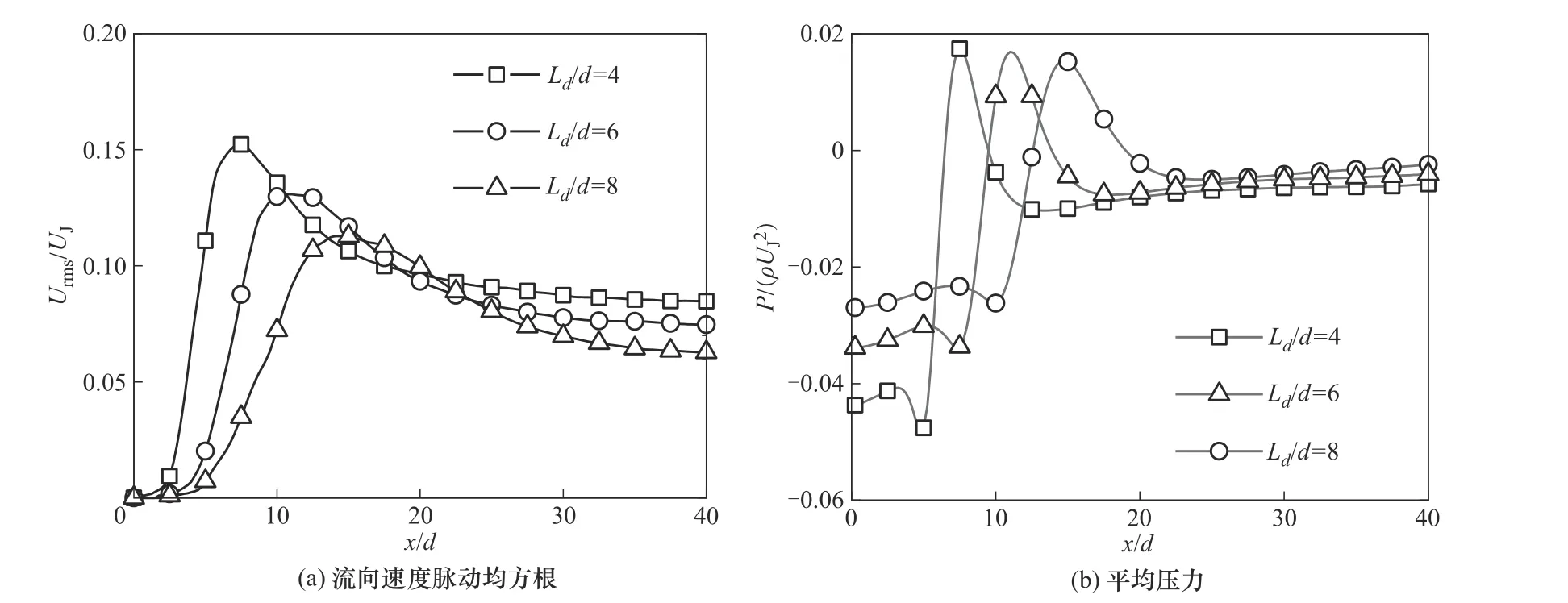
图7 中心线上流场统计特性流向演化Fig.7 Streamwise evolution of the flow characteristics along the center line
在分析三种射流口间距下中心线上流场统计特性后,本文将探究反应物和生成物的标量统计特性。图8~图10分别为射流口间距Ld/d=6下各组分同一时刻瞬时浓度云图和平均浓度云图。反应物A、B和产物R浓度分别以ГA0、ГB0和ГR0=ГA0ГB0/(ГA0+ГB0)无量纲化,这与Watanabe等的研究[16]中无量纲过程相同。图中黑色分别代表反应物A 的浓度为ГA/ГA0=1、反应物B的浓度为ГB/ГB0=1以及产物R的浓度为ГR/ГR0=1,两条黑色虚线代表回流区两端位置。从图8~图10中可以看出,射流Ⅰ中的反应物A和射流Ⅱ中的反应物B随着流场发展在中心线上接触混合并扩散到彼此射流内部,在此过程中发生化学反应并产生产物R,回流区内产物浓度明显高于其附近区域,且回流区后随着流场发展产物的法向分布更为广泛。

图8 反应物A的瞬时浓度和平均浓度Fig.8 Instantaneous concentration and mean concentration of reactant A
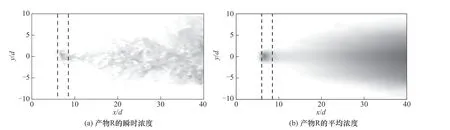
图10 生成物R的瞬时浓度和平均浓度Fig.10 Instantaneous concentration and mean concentration of product R
根据Watanabe 等[17]的单束反应性射流标量场可视化研究,瞬时化学反应速率可以表达为W^R=DaГAГB/(ГA0ГB0),图11 为关于产物R 的瞬时化学反应速率W^R云图。图中白色代表W^R= 0,黑色代表W^R= 0.01,三条黑色竖虚线分别代表准滞止点位置、混合点位置和合并点位置,黑色横虚线代表流场中心线。由图11可知,回流区和混合区化学反应主要发生在流场中心线附近,而在混合点后化学反应发生在围绕流场中心线法向更广的范围,且在流场下游化学反应较弱。
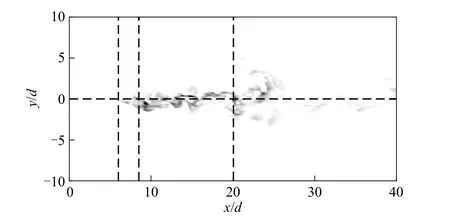
图11 瞬时化学反应速率Fig.11 Instantaneous chemical reaction rate
图12(a)、(b)为三种射流口间距下中心线上反应物A 和B 无量纲平均浓度ГA/ГA0和ГB/ГB0流向演化。反应物浓度在回流区内急剧升高,在混合点后维持在较高水平,这是因为回流作用将混合点附近双射流携带的反应物输运到回流区前部,混合点后随着流场发展反应物不断向中心线上输运。图12(c)为三种射流口间距下中心线上产物R的无量纲平均浓度ГR/ГR0流向演化,产物浓度沿中心线在回流区内存在一个峰值。结合图7(b)、图8、图9,回流区内反应物A和B会充分混合并产生产物R,而混合点两股射流碰撞产生的高压区会阻碍产物向下游输运,从而导致存在上述峰值。此外,随着射流口间距增大,反应物平均浓度峰值减小且峰值位置后移,产物平均浓度峰值增大且峰值位置后移。
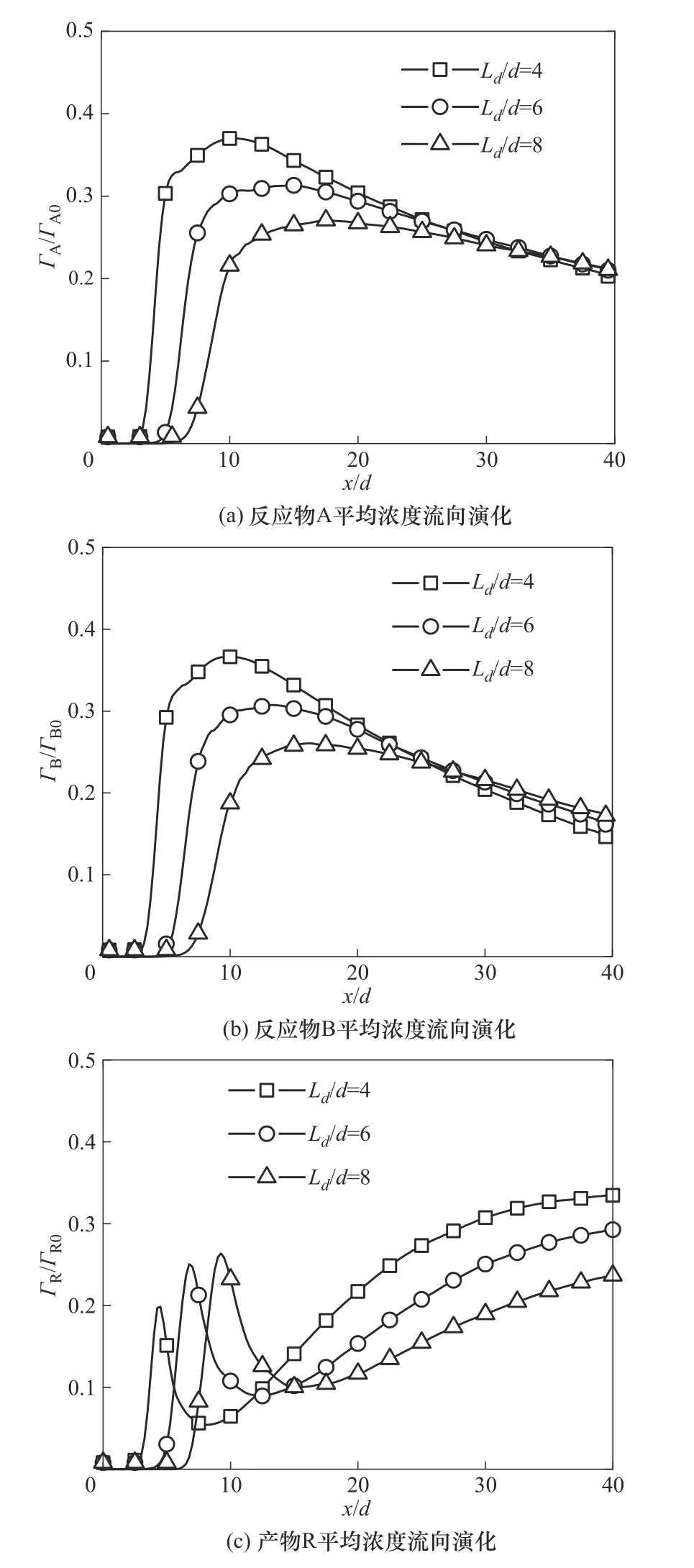
图12 中心线上平均反应物浓度和平均产物浓度流向演化Fig.12 Streamwise evolution of the mean concentration of reactant and product along the center line
图13(a)、(b)分别为三种射流口间距下反应物A和反应物B的无量纲浓度脉动均方根ГArms/ГA0和ГBrms/ГB0沿中心线的流向演化。反应物浓度脉动均方根在回流区急剧增加,这与前人关于双射流湍动能研究中湍动能流向演化趋势类似[32],该急剧变化是由回流区卷吸作用的扰动所引起的。图13(c)为三种射流口间距下产物R无量纲浓度脉动均方根ГRrms/ГR0沿中心线的流向演化。产物浓度脉动均方根在流场上游存在两个峰值且峰值位置分别与准滞止点和混合点接近。第一个峰值出现的原因是回流区前反应物A 和B 在准滞止点附近一个反应-不反应界面刚开始接触并发生反应,此时产物R 浓度脉动极强。第二个峰值出现的原因是混合点附近反应物A和B随着两股射流碰撞剧烈反应。上述演化都是对流、化学反应、扩散过程综合作用的结果,3.3节将结合标量输运方程给出详细分析。本节对流场和标量场的分析表明,随着射流口间距的改变反应物和产物的标量场都呈一定规律的改变,流动在准滞止点和混合点附近的行为直接影响着化学反应。
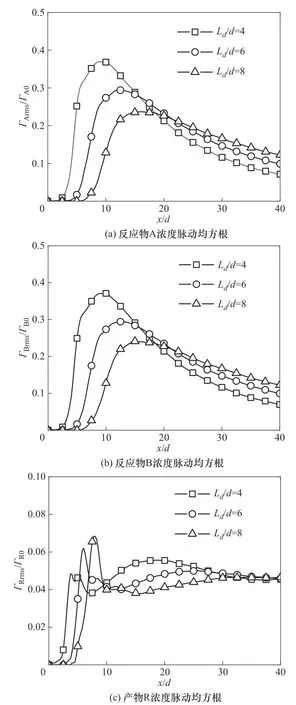
图13 中心线上反应物浓度脉动均方根和产物浓度脉动均方根流向演化Fig.13 Streamwise evolution of concentration fluctuation rms value of reactant and product along the center line
3.2 射流相互作用尺度
3.1 节分析发现中心线上湍流流场和标量场统计量的流向演化与射流口间距存在一定规律。Zhou等[5]基于单射流幂率和湍流/非湍流界面层概率密度函数首次提出射流相互作用尺度x*(x*=Ld),指出不同射流口间距下湍流特性的流向演化均以x*为尺度,即当以x*对流向距离x无量纲时不同射流口间距下中心线上湍流统计量的流向演化曲线会重合。本节将射流相互作用尺度引入反应性双射流,探究反应性双射流中标量统计量的空间演化是否遵循上述规律。
图14(a)、(b)分别为三种射流口间距下中心线上无量纲反应物A 平均浓度〈ГA〉/〈ГA〉max和反应物B 平均浓度〈ГB〉/〈ГB〉max的流向演化,其中流向距离x以x*无量纲化。在流场中心线上整个流域无量纲反应物平均浓度曲线有相当好的重合,这表明x*可以作为潜在的描述反应物标量统计量的相互作用尺度。为了充分考察x*在反应物标量场的适用性,图15(a)、(b)给出了三种射流口间距下中心线上无量纲反应物浓度脉动均方根ГArms/ГArms,max和ГBrms/ГBrms,max流向演化情况,其中流向距离x以x*无量纲化。从两图可以看出反应物浓度脉动均方根三条曲线在整个流域也均有相当好的重合,这表明x*可以作为描述反应物标量统计量的相互作用尺度。值得一提的是,Run J4 的曲线与Run J6 和Run J8 的曲线略有偏差,本文认为这是由射流口间距过小进而出现了Mondal 等[9]提出的周期性涡脱落现象所导致的,这与射流口间距在6<Ld<8 范围内反应物标量统计量的空间演化规律并不冲突。
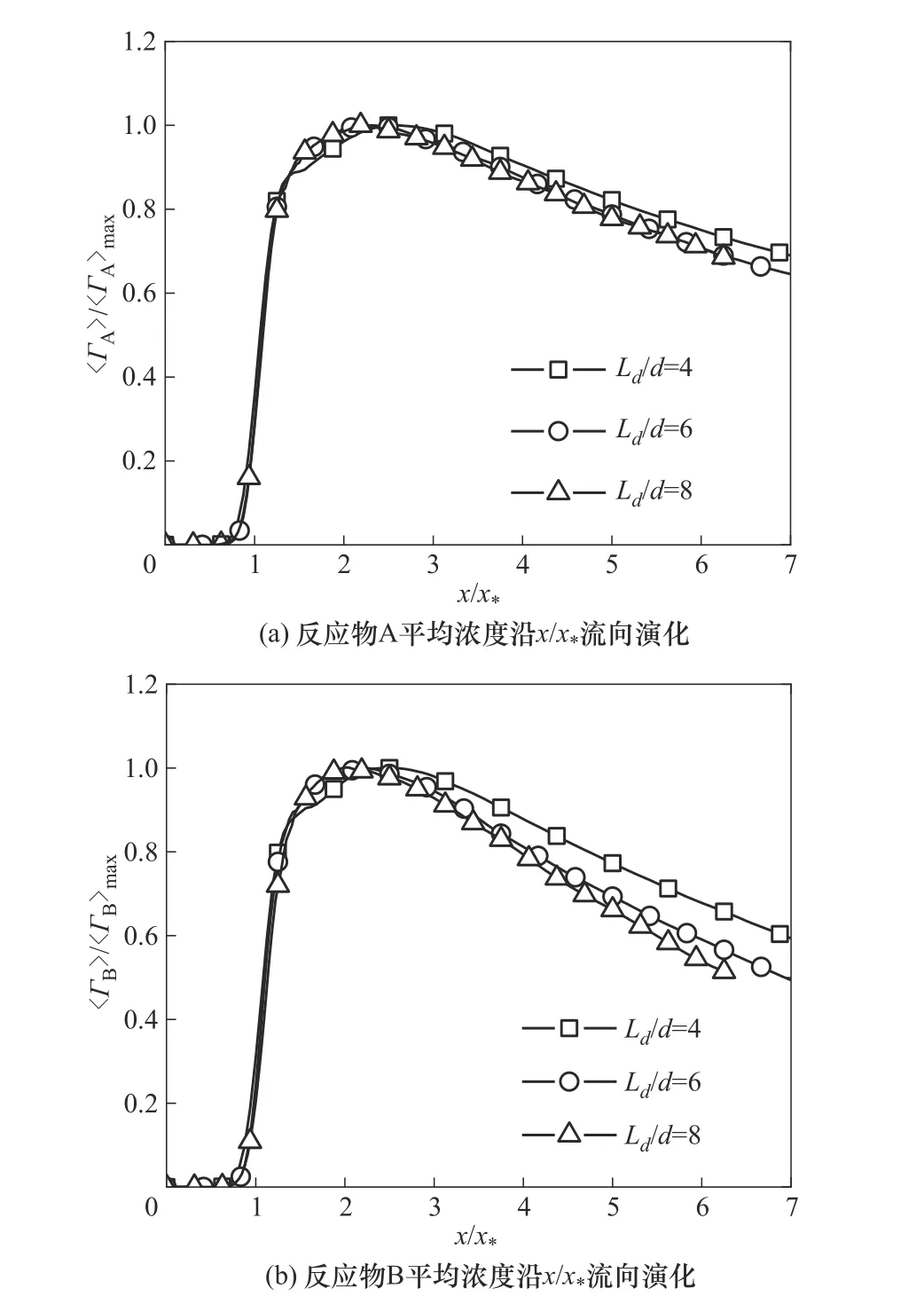
图14 反应物A和反应物B平均浓度沿着中心线上x/x*的流向演化Fig.14 Streamwise evolution of the mean concentration of reactant A and reactant B along x/x*on the center line
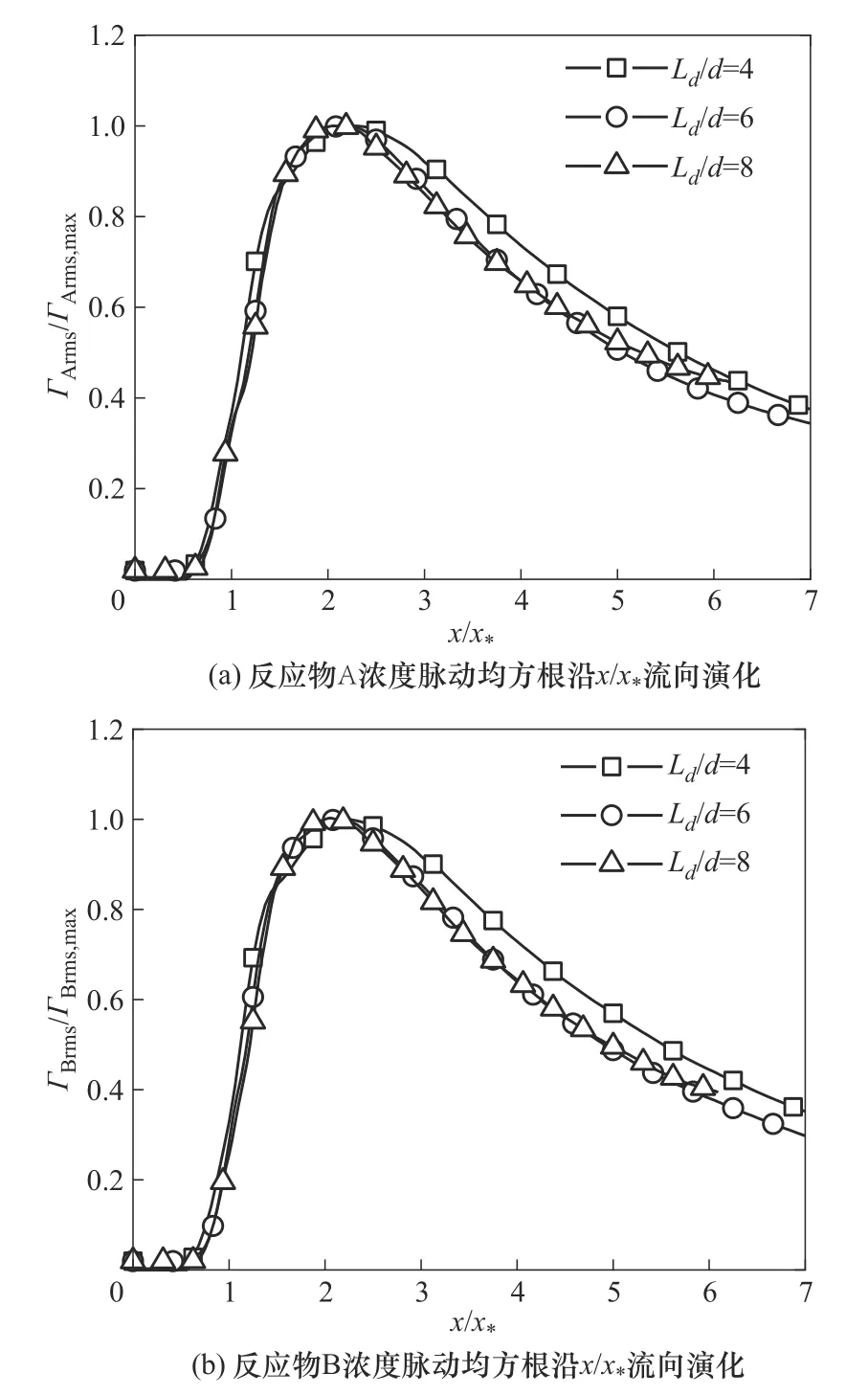
图15 反应物A和反应物B浓度脉动均方根沿着中心线上x/x*的流向演化Fig.15 Streamwise evolution of reactant A and reactant B concentration fluctuation rms value along x/x*on the center line
图16(a)、(b)分别为三种射流口间距下中心线上无量纲产物R 平均浓度〈ГR〉/〈ГR〉max和浓度脉动均方根ГRrms/ГRrms,max的流向演化,其中流向距离x以x*无量纲化。图16(a)中Run J6 和Run J8 的无量纲平均产物浓度曲线在整个流域内有良好重合,表明x*可以作为潜在的描述产物标量统计量的相互作用尺度。图16(b)中Run J6 和Run J8 的无量纲产物浓度脉动均方根曲线在流场上游(x/x*<1.2)有较好重合,这表明x*可以作为描述产物标量统计量在上游演化的相互作用尺度。此外,Run J4 的曲线与Run J6 和Run J8 的曲线在下游偏差较大,这表明周期性涡脱落现象对产物浓度脉动的影响比对反应物浓度脉动的影响更大。
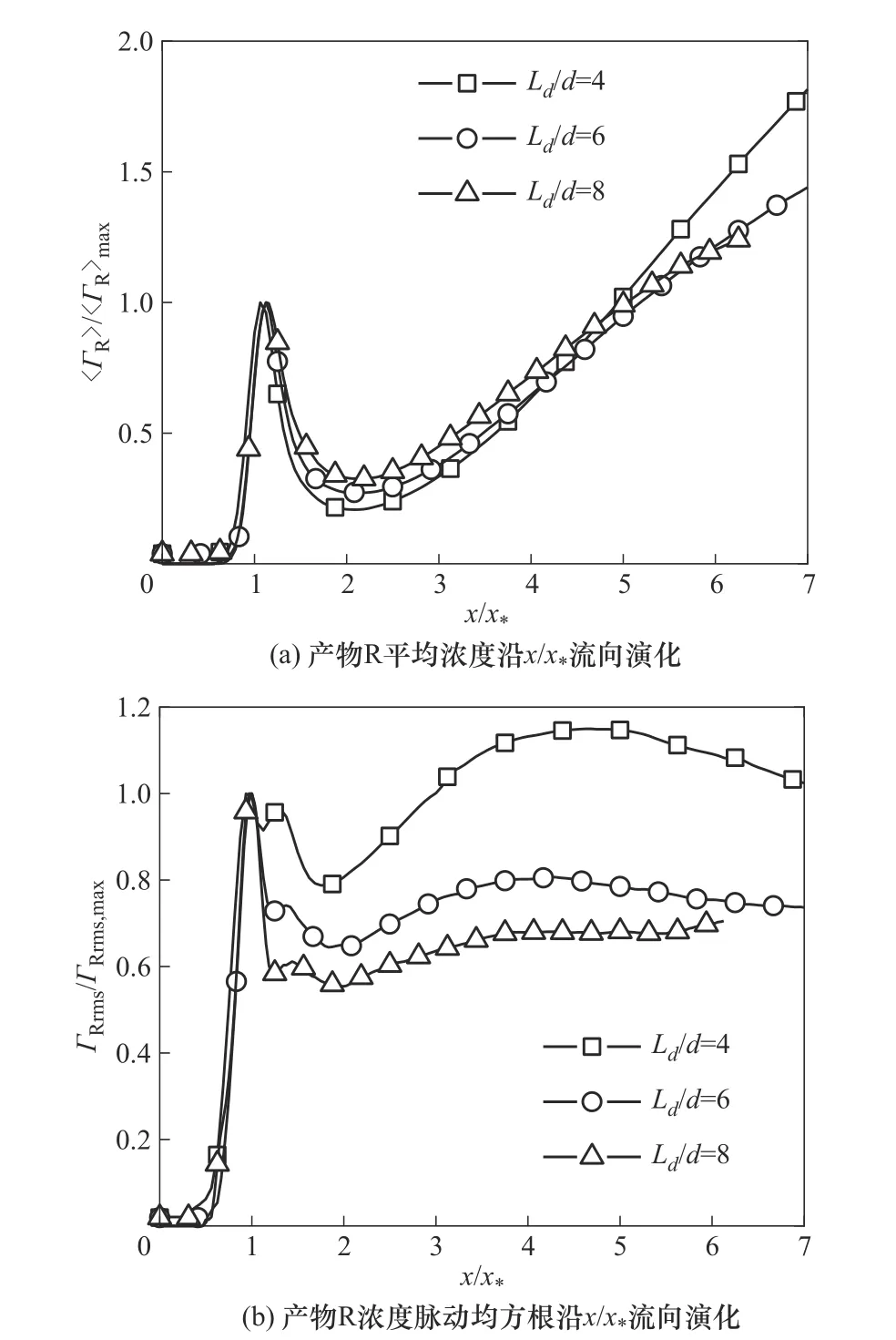
图16 产物R平均浓度和浓度脉动均方根沿着中心线上x/x*的流向演化Fig.16 Streamwise evolution of concentration and concentration fluctuation rms value of product R along x/x*on the center line
表3给出了三种射流口间距下无量纲射流相互作用尺度x*、反应物A 浓度脉动均方根峰值位置xpeak、产物R 浓度脉动均方根峰值位置(xpeak1和xpeak2)和对应的无量纲化比值。其中,比值分别由Run J4算例的对应值(x*1,xpeak1,xpeak1,1和xpeak2,1)无量纲化。可以看出反应物浓度脉动峰值位置xpeak和产物浓度脉动峰值位置(xpeak1和xpeak2)均与射流相互作用尺度x*呈一定的线性关系。此外,本文也以xpeak等尺度对流向距离无量纲化得到了不同射流口间距下的反应物和产物标量统计量的流向演化曲线,其结果与图14~图16 中曲线类似,在此不再赘述。上述结果表明xpeak,xpeak1和xpeak2也可以作为描述反应性双射流中标量统计量的相互作用尺度。
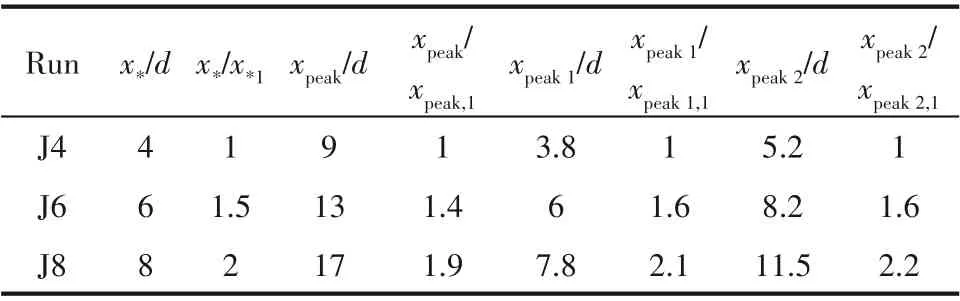
表3 无量纲射流相互作用尺度x*、反应物浓度脉动均方根峰值位置xpeak和产物浓度脉动均方根峰值位置xpeak 1、xpeak 2Table 3 Normalized wake-interaction scale x*,locations of reactant concentration fluctuation rms peak xpeakandproduct concentration fluctuation rms peak xpeak 1,xpeak 2
由于本文考虑的是Da=0.1 的弱化学反应过程,反应物标量特性主要受双射流间相互作用影响,当前双射流相互作用尺度可以预测整个流域的反应物平均浓度和反应物浓度脉动均方根的流向演化。产物标量特性受射流间相互作用和标量相互作用影响,故产物平均浓度和产物浓度脉动均方根的流向演化较为复杂。尽管如此,当前相互作用尺度也可以预测上游(x/x*<1.2)的产物标量统计量的流向演化。综上讨论,在一定的射流口间距范围内(6<Ld<8),如果使用适当的尺度(如本文中的x*和xpeak等)对流向距离无量纲化,不同射流口间距下射流相互作用中的标量统计特性演化遵循相似的规律。因此,下文的研究只考虑Ld/d=6一种情况。
3.3 标量产生、消耗和输运
3.3.1 化学反应标量输运方程 化学反应标量输运方程是研究标量产生、消耗和输运的重要方法。反应物A、B 和产物R 的化学反应标量输运方程分别为:


图17(a)、(b)分别为关于反应物A 和B 的化学反应标量输运方程中各项瞬时值的流向演化。RHS为残差项表示公式左右两侧代数差。RHS 在中心线流向上几乎为0,表明标量场统计结果有良好收敛性。图中三条虚线分别代表流场的准滞止点位置(Ld/d=6)、混合点位置(Ld/d=8.5)和合并点位置(Ld/d=20)。因为两束射流所携带的反应物还没有被输运到流场中心线,化学反应尚未发生,所以在流场上游回流区前(x/d<6)标量输运方程中各项均为0。当x/d>6 时,对流项A和非稳态项At沿着中心线呈正负值交替变化,而扩散项D和化学反应源项S相对于对流项A和非稳态项At可以忽略。这表明对流输运作用主导反应物浓度变化,而化学反应和扩散作用较弱且对反应物浓度标量的输运几乎没有影响,故式(9)和式(10)可以分别简化为:

此外,在图17(a)、(b)中还可以看出回流区内(6<x/d<8.5)对流项的值比混合区(8.5<x/d<20)和合并区(x/d>20)对流项的值小得多。这是因为两股射流在混合点直接碰撞,碰撞前回流引起的输运作用较小而碰撞后对流作用较强。
图18 为产物R 的化学反应标量输运控制方程中各项瞬时值的流向演化。当x/d>6 时,对流项AR和非稳态项AtR沿着中心线呈正负值交替变化,化学反应源项SR相对于对流项AR和非稳态项AtR较小,扩散项DR可以忽略。这表明化学反应产生的产物被对流作用输运,对流作用仍主导反应物浓度变化,扩散作用对产物的输运几乎没有影响,故式(11)可以简化为:

由式(12)~式(14)、图17、图18 可以看出对流作用和非稳态变化之间存在一定负相关性,引入相关系数ρ[33]以定量探究对流项和非稳态项的相关性以及控制方程中其他各项彼此间相关性。以对流项A和非稳态项At为例,相关系数由式(15)给出:
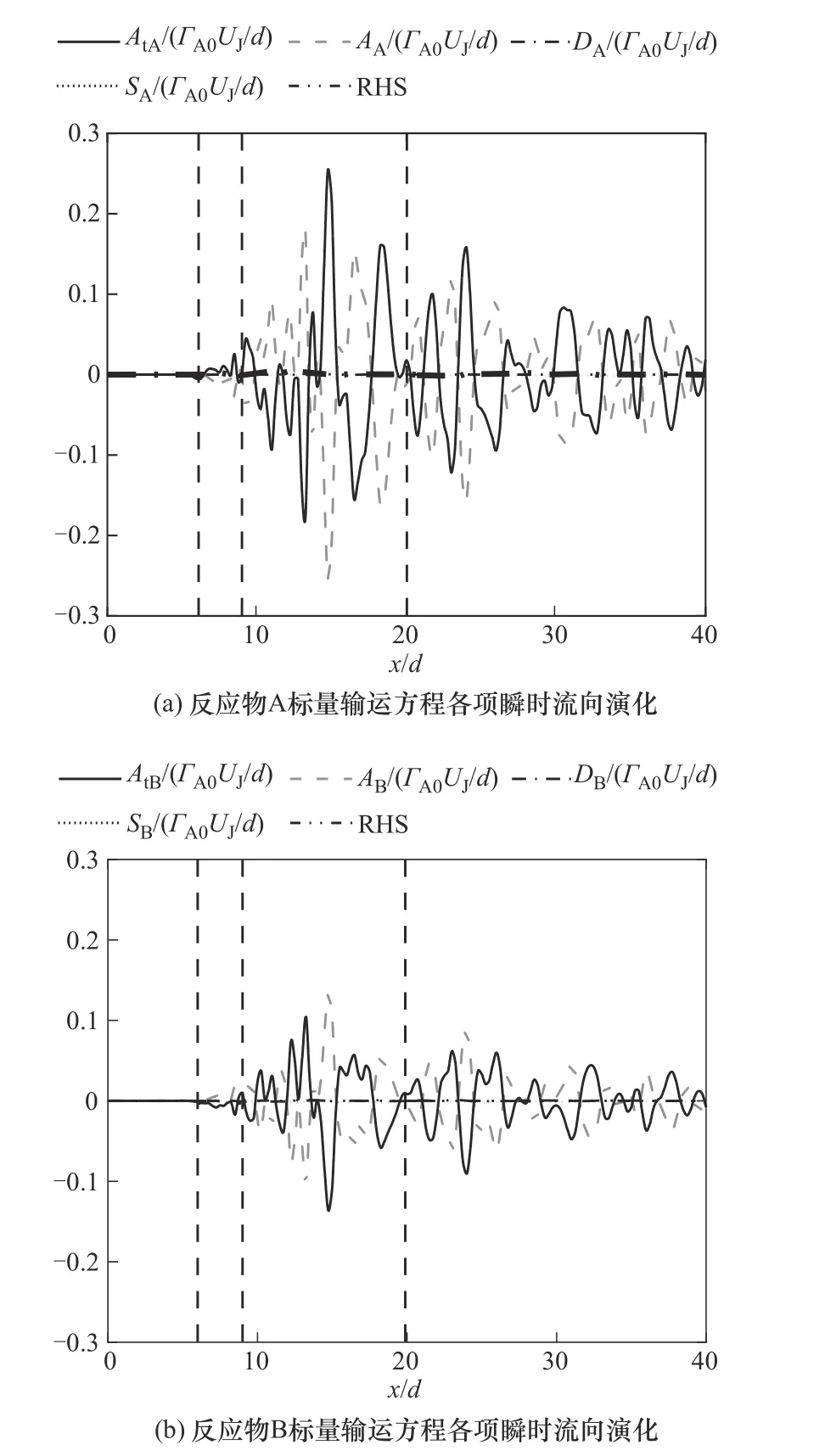
图17 反应物标量输运方程各项沿着中心线的瞬时流向演化Fig.17 Streamwise evolution of the instantaneous terms in reactant scalar transport equation along the center line
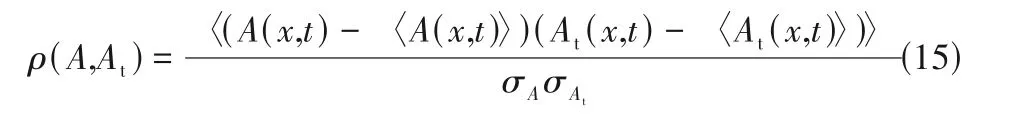
式中,σ为标准差。由于x/d<6时各项均为0,本文研究x/d>6 时反应物和产物标量输运方程中各项之间相关性。图19(a)、(b)分别为反应物A 和B 标量输运方程中各项间相关系数在中心线上流向演化,ρ(AA,AtA)和ρ(AB,AtB)几乎保持在-1,ρ(DA,AtA)、ρ(DB,AtB)、ρ(SA,AtA) 和ρ(SB,AtB)几乎为0,这表明反应物浓度非稳态变化几乎由对流过程主导,与上文图18的分析一致。反应物标量输运方程中其他各项间相关 系 数[ρ(AA,DA)、ρ(AA,SA)、ρ(DA,SA)、ρ(AB,DB)、ρ(AB,SB)和ρ(DB,SB)]很小,说明扩散过程、化学反应过程和对流过程彼此间影响很小。图19(c)为产物R标量输运方程中各项相关系数在中心线上流向演化。ρ(AR,AtR)几乎保持在-1,表明产物R浓度非稳态变化也几乎由对流过程主导。ρ(SR,AtR)相关系数在混合区(8.5<x/d<20)的值大于其他区域,表明混合区化学反应较为剧烈,对产物R 浓度非稳态变化的影响减弱。此外,ρ(DR,SR)维持在-0.4~-0.15 之间,表明化学反应产生的产物R也由扩散过程输运。
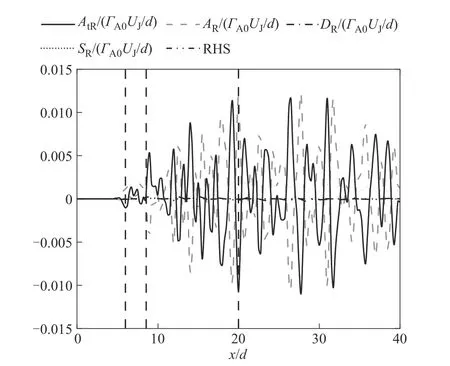
图18 产物标量输运方程各项沿着中心线的瞬时流向演化Fig.18 Streamwise evolution of the instantaneous terms in product scalar transport equation along the center line
上文提到图19(c)中的ρ(AR,AtR)几乎保持在-1,对流项与非稳态项呈强烈负相关特性,为进一步探究这一负相关性,图20 给出了非稳态项脉动AtR-〈AtR〉与对流项脉动AR-〈AR〉在x/d=10,20和30处的联合概率密度分布(JPDF)。标示的六个等值线的值分别为0.3,0.1,0.03,0.01,0.003 和0.001。AtR-〈AtR〉与AR-〈AR〉在三个位置的JPDF 几乎均挤压在y=-x直线上,印证了产物R 浓度非稳态变化也几乎由对流过程主导。该JPDF在x/d=10处被挤压效果不如在x/d=20和30处明显,这是因为x/d=10所在的混合区化学反应相对较强,此时非稳态项和对流项间相关性较弱。
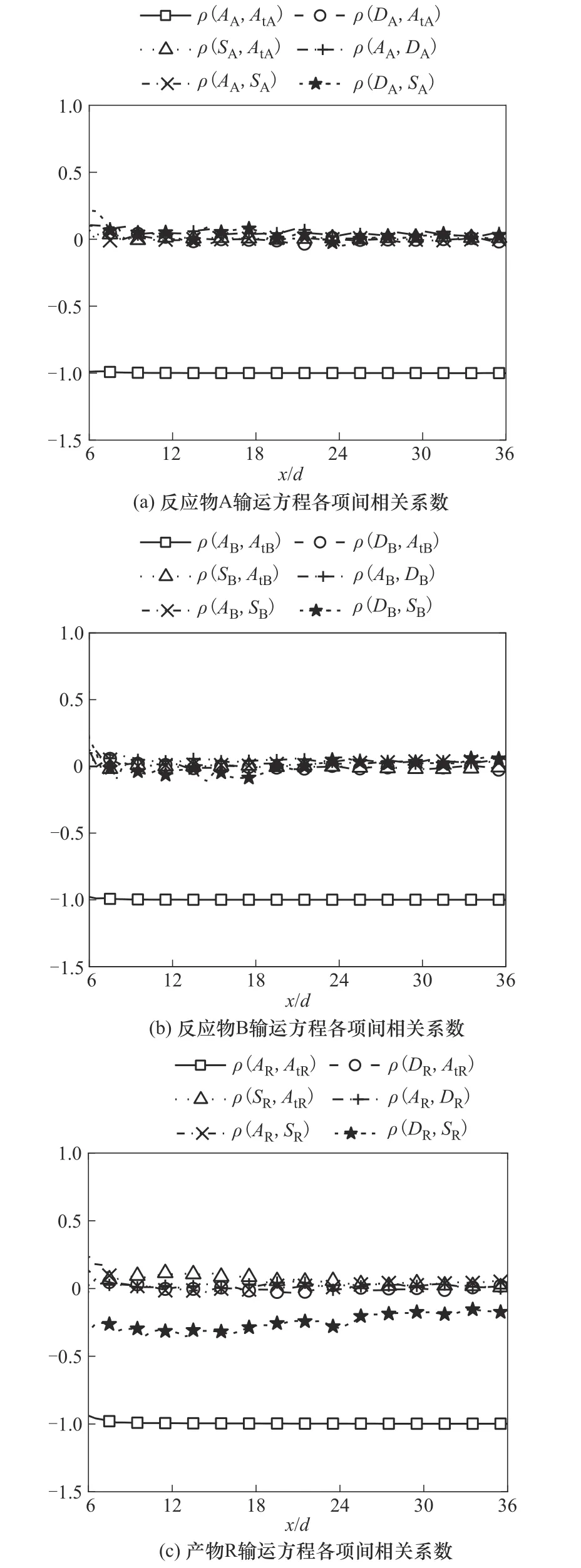
图19 化学反应输运方程各项间相关系数沿着中心线的流向演化Fig.19 Streamwise evolution of the correlation coefficient between items of the chemical reaction transport equation along the center line
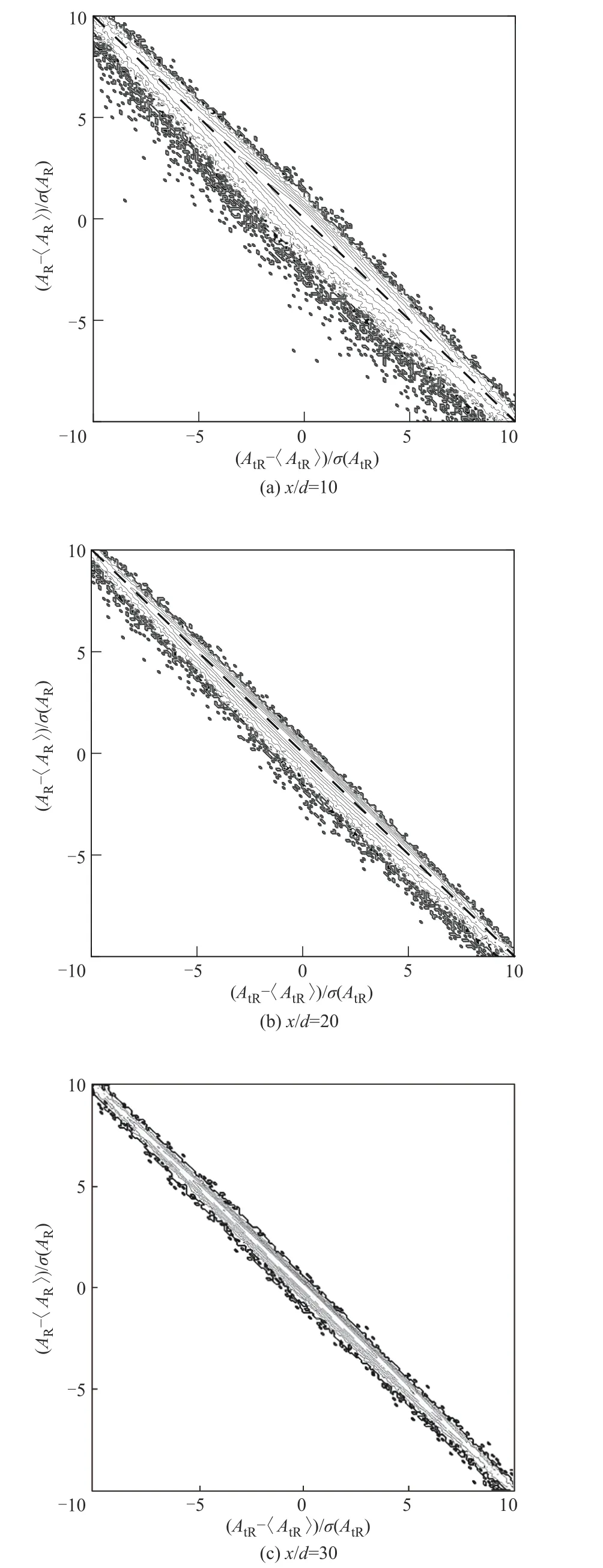
图20 AtR-〈AtR〉和AR-〈AR〉在x/d=10,20和30处的联合概率密度分布Fig.20 JPDF of AtR-〈AtR〉and AR-〈AR〉at x/d=10,20,and 30
对图19(c)的分析中还指出ρ(DR,SR)维持在-0.4~-0.15 之间,扩散项与化学反应源项有弱负相关性。同样,为进一步探究这一负相关性,图21 给出扩散项脉动DR-〈DR〉与化学反应源项脉动SR-〈SR〉在x/d= 10, 20 和30 处的联合概率密度分布。标示的五个等值线的值分别为0.1,0.03,0.01,0.003 和0.001。可以看出JPDF 在流向三个位置关于y= -x都有一定的对称性,这与相关系数ρ(DR,SR)的流向演化相符。
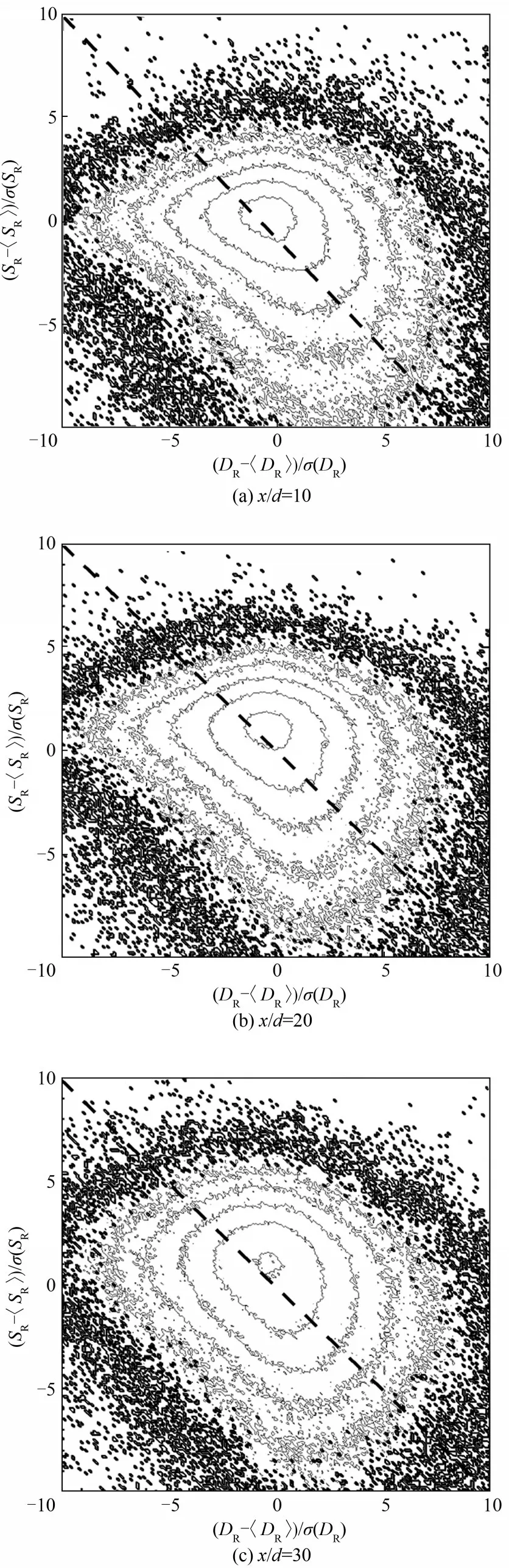
图21 DR-〈DR〉和SR-〈SR〉在x/d=10,20和30处的联合概率密度分布Fig.21 JPDF of DR-〈DR〉and SR-〈SR〉at x/d=10,20,and 30
图22(a)~(c)为各项平均值的流向演化。对流项〈A〉和化学反应源项〈S〉的值在整个流域几乎相等,这表明对流运动与化学反应引起的产物R的浓度变化收支平衡。关于产物R的稳态方程可以写为:
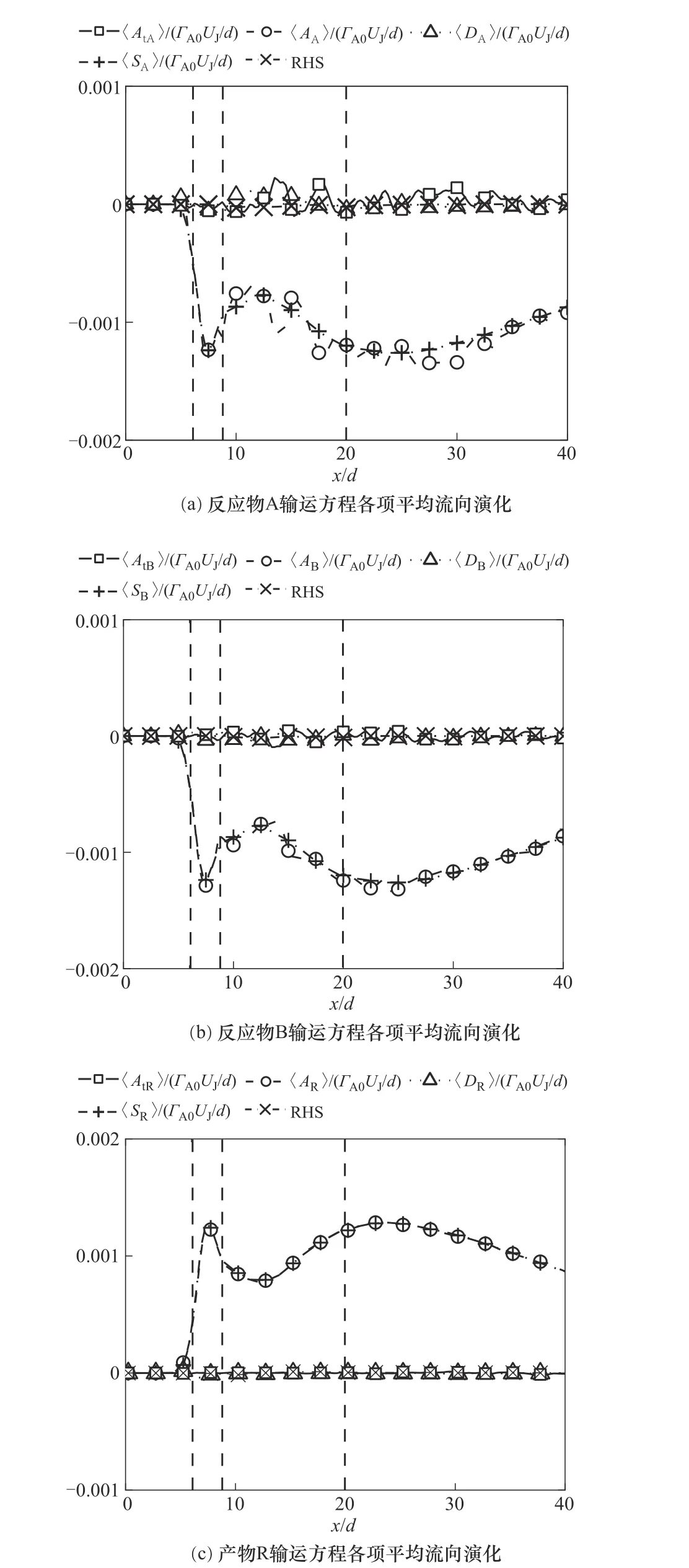
图22 化学反应标量输运方程中各项平均值沿着中心线的流向演化Fig.22 Streamwise evolution of the mean value of each term in chemical reaction scalar transport equation along the center line

此外,沿着流场中心线有两个化学反应较强的峰值点。回流作用使反应物A 和B 不能向下游输运,在混合点前充分混合并反应,回流区域内出现第一个峰值。随着流场发展两股射流逐渐吸引,在混合点合并为一股射流后对流作用不再增强,合并点后出现第二个峰值。
在当前研究中(Da=0.1 且Sc=0.71)双射流标量特性受化学反应影响相对较弱。从图17、图18瞬态输运方程各项的流向演化可以看出,由双射流携带的反应物A 和B 几乎由对流过程输运,化学反应引起反应物消耗很小,由化学反应产生的产物R 也几乎由对流过程输运。从图22 输运方程各项平均值的流向演化可以看出,对流项与化学反应源项相互抵消,混合点前回流作用使化学反应增强。流场上游化学反应最为剧烈的点存在于回流区内回流速度最大的点附近,流场下游化学反应较为剧烈的点出现在合并点后一段距离。
3.3.2 反应物和产物浓度相关性 反应物和产物各浓度间相关性可以反映出流动与化学反应的耦合关系。图23 为各组分浓度相关系数在中心线上的流向演化,反应物A 瞬时浓度和反应物B 瞬时浓度相关系数ρ(ΓA,ΓB)维持在-0.9,呈现强烈负相关特性。图24 为反应物输运方程中对流项AA和AB间相关系数ρ(AA,AB)的流向演化。自混合区后对流项AA和对流项AB呈负相关,这导致了反应物A 和反应物B 浓度呈负相关,这一结果与图17 的结论相符。反应物浓度的负相关特性表明随着化学反应的发生混合区后射流中心线上反应物A的出现会引起反应物B 的减少,同时反应物B 的出现也会引起反应物A 的减少。此外,反应物A 和产物R 浓度之间相关系数ρ(ΓA,ΓR)维持在0 左右,这是因为组分浓度间的相关性与化学反应有关,而射流中心线上反应物A浓度变化主要由对流作用引起且化学反应对反应物浓度影响较弱,故反应物A 和产物R 浓度之间相关性很弱。反应物B和产物R 浓度之间相关系数ρ(ΓB,ΓR)在-0.25~0 之间变化,同样呈一定弱负相关特性。ρ(ΓA,ΓR)和ρ(ΓB,ΓR)的值不同是由反应物B的初始浓度比反应物A的初始浓度小导致的。
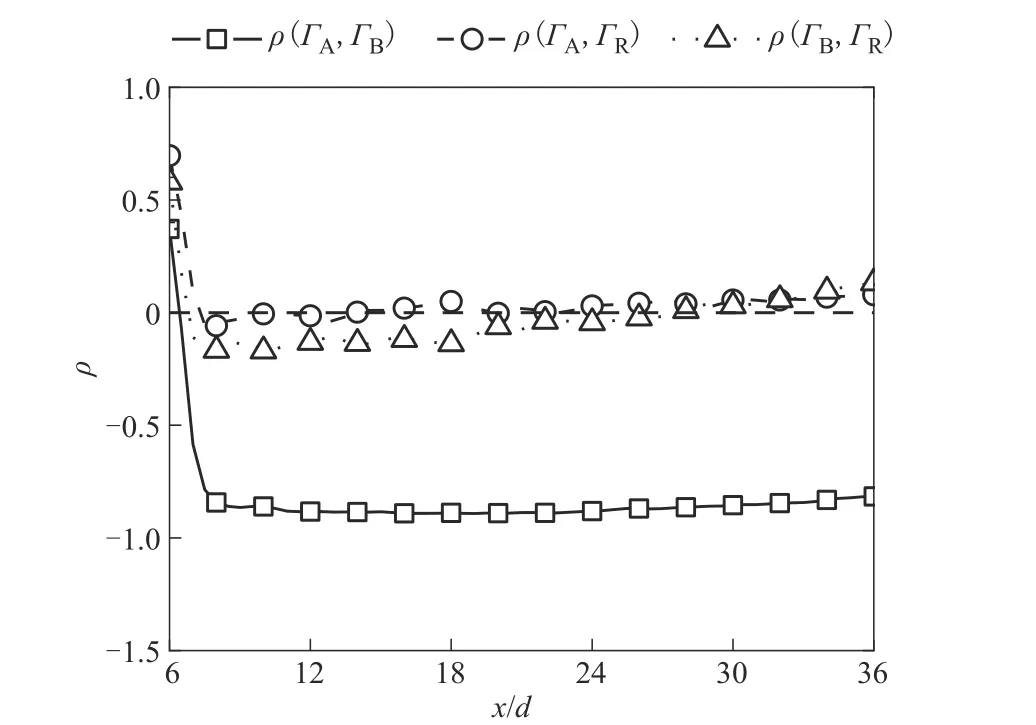
图23 组分浓度间相关系数沿着中心线的流向演化Fig.23 Streamwise evolution of the correlation coefficient between the component concentrations along the center line
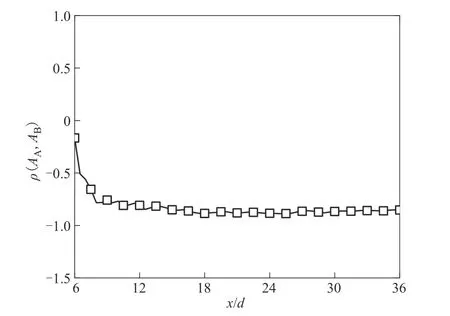
图24 反应物输运方程中对流项AA和AB间相关系数ρ(AA,AB)沿着中心线的流向演化Fig.24 Streamwise evolution of the correlation coefficient ρ(AA,AB)between the advection term AA and AB in the transport equation of reactant along the center line
反应物浓度脉动和产物浓度脉动的联合概率密度分布一定程度上可以反映化学反应对各组分浓度的影响。图25 给出了反应物A 和产物R 浓度脉动之间的JPDF,标示的五个等值线的值分别为0.1, 0.03, 0.01 , 0.003 和0.001。在x/d=10,20 和30处,该JPDF 呈“心形”。此外,反应物B 和产物R 浓度脉动之间JPDF的形状与其几乎相同,本文不再给出。从JPDF 可以看出在三个位置处反应物A 浓度和反应物B 浓度脉动较大时,产物R 浓度大概率维持在较低水平。只有反应物A 瞬时浓度和反应物B瞬时浓度都在平均值时,产物R 浓度有较大概率维持在较高水平,有利于化学反应的发生。
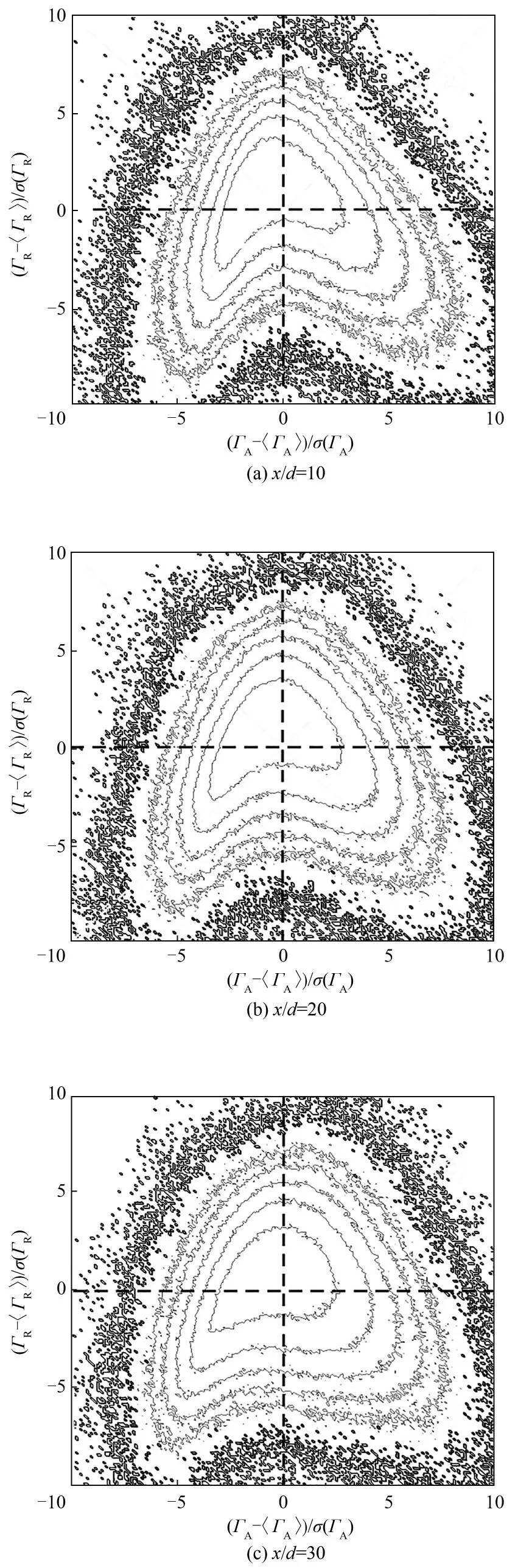
图25 ΓA-〈ΓA〉和ΓR-〈ΓR〉在x/d=10,20 和30 处的联合概率密度分布Fig.25 JPDF of ΓA-〈ΓA〉and ΓR-〈ΓR〉at x/d=10,20,and 30
4 结 论
对具有二级非平衡基元反应的双射流进行了数值模拟研究,具体研究了三种射流口间距下在Da= 0.1、Sc= 0.71 时化学反应、对流作用和扩散作用对反应物消耗、产物产生和组分输运的影响。主要结论如下。
(1)流动在准滞止点和混合点的行为直接影响着化学反应。流场上游产物浓度均方根脉动有两个峰值,两个峰值位置分别在准滞止点xqsp和混合点xmp附近。
(2)x*可以作为预测反应性双射流中标量输运特性的射流相互作用尺度。在一定的射流口间距范围内,使用适当的尺度(如x*和xpeak)对流向距离无量纲化,不同射流口间距下标量统计量演化遵循相似规律。
(3)在Da=0.1 且Sc=0.71 时,双射流标量输运特性受化学反应影响较弱。由双射流携带的反应物A和B几乎由对流过程输运(AtA=-AA,AtB=-AB),由化学反应产生的产物R 也几乎由对流过程输运(AtR=-AR+SR)。统计平均下对流运动与化学反应引起的产物R的浓度变化收支平衡(〈AR〉=〈SR〉)。
(4) 反应物A 浓度脉动和反应物B 浓度脉动具有较强负相关性。反应物A瞬时浓度和反应物B瞬时浓度均在平均值时,产物R 浓度有较大概率维持在较高水平,有利于化学反应的发生。
符 号 说 明
A——对流项
At——非稳态项
D——扩散项
Dα——分子扩散系数,m2/s
P——压力,Pa
S——化学反应源项
t——时间,s
Ui——i方向上的速度U、V和W,m/s
xi——x、y和z方向坐标,m
Γ——物质的量浓度,mol/L
ν——运动黏度,m2/s
下角标
C——双射流中心线
i——自由指标
j——哑指标
α——反应物或产物组分A、B或R

