高中数学教学中逻辑推理素养的培养路径
孟 伟
(安徽省蒙城县第六中学 233500)
高中数学课程标准明确指出逻辑推理素养是核心素养的主要构成部分,并介绍了有关逻辑推理素养的相关知识以及在教学中的具体要求.教学实践中应充分学习与把握逻辑推理素养内涵,将逻辑推理素养培养纳入教学工作的重点.
1 灌输逻辑推理理论
高中数学教学中为更好地培养学生的逻辑推理素养应使学生认识到什么是逻辑推理,逻辑推理包含哪些形式,提升逻辑推理素养的必要性等,使其更加积极地配合培养工作.一方面,为学生介绍归纳推理、类比推理、演绎推理等不同的推理形式,使其认识到这些推理形式均是逻辑推理的范畴,尤其针对相关的数学问题应与学生一起分析应用的是何种推理形式,使学生搞清楚数学结论的来龙去脉,进一步加深其印象的同时体会逻辑推理的整个过程.另一方面,为使学生搞清楚推理形式之间的区别,加深学生对逻辑推理理论的理解,课堂上注重与学生进行互动,尤其注重提问学生代表,并纠正其认识与理解上的不足.
归纳推理是高中数学中的常见逻辑推理形式,在解答高中数学习题中有着广泛的应用,为学生讲解相关理论知识后可结合以下数学问题,为学生剖析归纳推理的过程:
例1数列{an}满足an+1+(-1)n+1an=2n,则数列{an}的前60项的和为( ).
A.1830 B.1820 C.1810 D.1800
该题是一道典型的数列习题.解题时可通过给出的等式关系,尝试着求解出前几项,而后通过归纳推理,得到相关项数之和的关系,再运用数列前n项和求和公式进行计算.
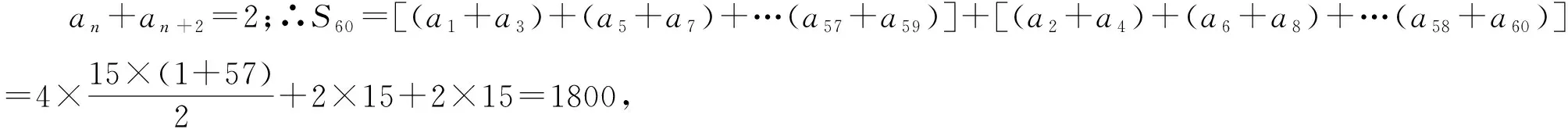
2 讲解逻辑推理例题
为使学生更好地把握运用逻辑推理解答数学习题的思路,锻炼学生的学以致用意识与能力,完成理论知识灌输后应注重结合具体教学内容做好相关例题讲解,使其更好地把握逻辑推理的精髓以及细节.一方面,高中数学习题灵活多变,解题应用的逻辑推理方法不尽相同,实践中应注重结合逻辑推理培养目标做好相关例题的认真筛选与设计,使学生不仅掌握破题的相关技巧,而且能够在推理的过程中全面地考虑问题.另一方面,讲解例题的过程中既要注重设计问题给学生带来启发,又要做好其过程的板书.不仅如此,在完成例题讲解后要让学生做好听课总结,总结数学问题是如何进行转化的,多扪心自问,认真揣摩与体会,把握逻辑推理的关键点,确保逻辑推理科学严谨,上下连贯.
函数是高中数学的重点与难点.在进行该部分知识教学中为使学生把握相关参数之间的内在联系,灵活的运用相关的逻辑推理方式进行解题,可为学生讲解如下例题:
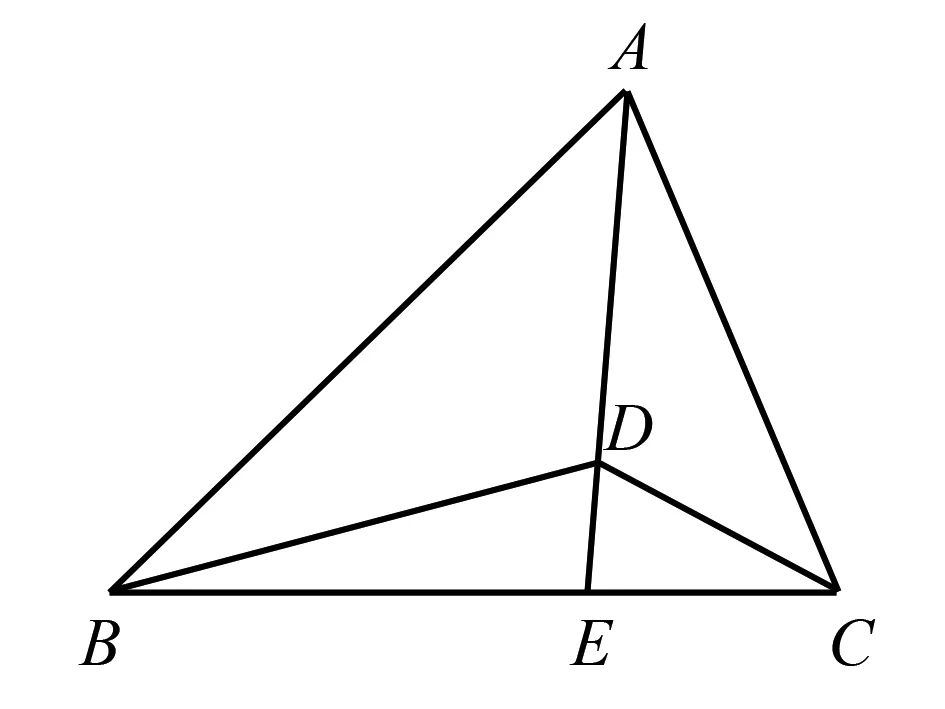
例2已知函数f(x)=log2x+1的定义域为[1,2],g(x)=f2(x)+f(x2)+m,若存在实数a、b、c∈{y|y=g(x)},使得a+b 在讲解该例题时应注重启发学生用换元法进行转化,达到化繁为简,有效解题的目的.不仅如此,要求学生认识到运用换元法进行推理时应确保换元前后参数取值范围一致,既不能扩大也不能缩小. ∵存在实数a、b、c∈{y|y=g(x)},使得a+b 逻辑推理对学生的认知推理能力具有一定要求,高中数学实践中培养学生的逻辑推理并不能一蹴而就,应注重将培养工作融入到日常的教学活动中,尤其积极组织学生开展逻辑推理训练活动,使学生能够针对不同的数学习题情境收集与挖掘推理的证据,积累逻辑推理的相关经验.一方面,开展逻辑推理训练活动时应注重与高中数学的重点知识结合在一起,尤其在训练习题的难度时应注重进行严格地把控,按照由易到难循序渐进的原则,如此既不会挫伤学生的积极性又能巩固学生所学,使逻辑推理能力得到针对性的锻炼.另一方面,课堂上完成逻辑推理训练后注重给学生预留讨论与交流的时间,使学生相互交流训练心得,借鉴他人逻辑推理时的相关技巧,不断提升自身的逻辑推理水平. 向量是高中数学的重要知识点,习题情境更是复杂多变.在高考中既可以单独出题,也可与其他知识点结合起来出题,只有熟练掌握基础知识以及相关的逻辑推理方法,才能高效地突破相关习题.在完成向量知识讲解后,为更好地锻炼学生的逻辑推理能力,可围绕以下习题组织学生开展课堂训练活动: 该题给出的已知条件较少.推理的过程中既需要应用向量的线性运算,又需要积极联系所学,根据习题情境合理的设出相关参数,寻找推理的切入点. 图1 高中数学教学中为确保逻辑推理素养培养目标的顺利达成,不能满足于学生已经掌握相关的推理技能,应注重结合学生实际做好学生推理能力拓展.一方面,做好学生学习现状的分析,总结学生的逻辑推理素养还有哪方面可提升的空间,做好针对性的教学设计,尤其要通过增加教学内容的难度,更好地拓展学生视野.另一方面,拓展学生推理能力时应注重多给予学生引导与启发,使其能够真正地从听课中顿悟,在明确自身逻辑推理不足的同时,真正的将所学转化为自身能力. 构造法是进行逻辑推理的常用方法.教学实践中,为使学生掌握运用构造法进行逻辑推理的思路,应注重在课堂上为学生讲解如下习题,进一步拓展学生的逻辑推理能力. 例4若asina-bsinb=b2-a2-1,则以下有关a、b的关系正确的是( ). A.a>bB.a 该题给出的已知条件较少,需要学生具备较强的逻辑推理能力.通过该习题的讲解,能达到拓展学生推理能力的目的. ∵asina-bsinb=b2-a2-1,∴asina+a2=bsinb+b2-1,令f(x)=xsinx+x2,∵f(-x)=(-x)sin(-x)+(-x)2=xsinx+x2=f(x),∴f(x)是偶函数,又∵f′(x)=sinx+xcosx+2x=x(cosx+1)+(sinx+x),令g(x)=sinx+x,则g′(x)=cosx+1≥0,则函数g(x)单调递增.当x≥0时,g(x)≥g(0)=0,∴当x>0时,f′(x)>0,函数f(x)单调递增.而因其为偶函数,则在x<0时,函数f(x)单调递减.∵f(a)=asina+a2,f(b)=bsinb+b2,而f(a)=f(b)-1,∴f(a) 高中数学教学中培养学生的逻辑推理素养是一个较为漫长的过程,需要渗透至教学的各个环节与教学内容之中,因此教学实践中应做好培养工作规划,积极寻找教学内容与培养工作之间的契合点,传授相关数学知识的同时通过讲解例题、开展训练以及拓展活动,使学生掌握逻辑推理丰富知识以及不同数学题型推理的有效切入点.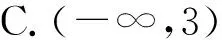
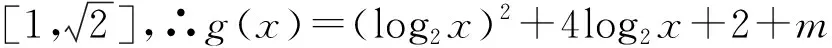
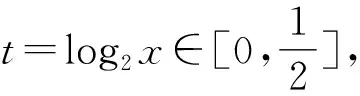
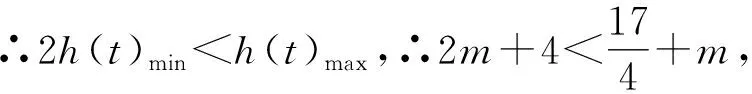
3 开展逻辑推理训练
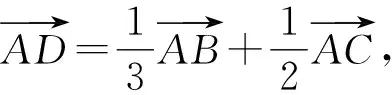
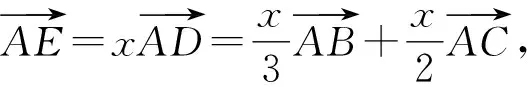
4 做好推理能力拓展

