构造函数在高中数学解题中的应用
魏春华
(福建省福州格致中学鼓山校区 350014)
函数是高中的重要内容,也是学生学习的一个难点,它贯穿于整个高中学习过程,数学中的构造函数是指基于对数学问题的合理抽象、深入理解,以及对初高中所学过的基本初等函数的认识,运用一个新的函数对原函数进行转化,以达到顺利求解问题的一种方法.构造函数是高中数学的重点与难点,对于学生的分析问题和解决问题的能力要求比较高,许多学生对题目理解困难,找不到破题之处,为使学生更好的掌握这一方法,既要做好相关理论知识的讲解,提高学生运用构造函数解题的意识,又要注重为学生展示其在解题中的具体应用过程,使学生更好的把握相关的应用细节与应用技巧,在这个过程中需要渗透构造的数学思维,并且需提升学生的运算能力.
例1(2020年全国数学高考一卷的21题)已知函数的f(x)=aex-1-lnx+lna(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;(2)若f(x)≥1,求a的取值范围.
此题的第二小题,很多学生在考试时候,由于题干十分的简单,不知该如何下手,直接求解不等式,似乎很难作答,然而如果尝试移项方式转化成恒成立问题,通过解决最值问题,就简化了求解的思路,进而可以快速的解出问题的答案.
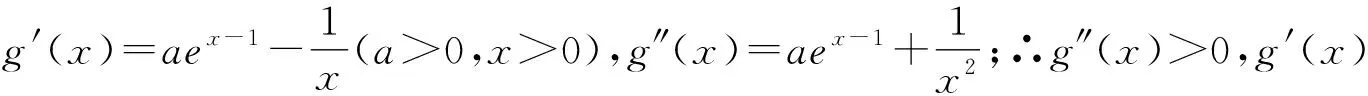
当x→0时,g′(x)→-∞,当x→+∞时,g′(x)→+∞,
∴存在唯一的x0使得g′(x0)=0,即在(0,x0)上g′(x)<0,(x0,+∞)上g′(x)>0
∴g(x)min=g(x0)=aex0-1-lnx0+lna-1
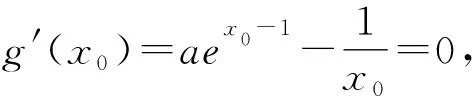
方法二:∵f(x)=aex-1-lnx+lna,∴f(x)=elnaex-1-lnx+lna=elna+x-1-lnx+lna≥1
∴elna+x-1+lna+x-1≥lnx+x=elnx+lnx,令g(x)=ex+x,即g(lna+x-1)≥g(lnx)
显然g(x)单调递增,所以lna+x-1≥lnx,即lna≥lnx-x+1,

∴h(x)max=h(1)=0,lna≥0,a≥1.
构造函数问题很具有挑战性,需要学生细心的观察能力和运算的能力,找到问题的突破口,构造出合理的函数从而解决问题.构造函数的问题应用十分的广泛,构造函数是对所学函数知识的综合应用,所有的基本初等函数都是构造问题的基础.构造满足条件的函数,要求对所有的基本初等函数的性质有深刻的理解,并能灵活的运用,常见的有以下几种情况:
1 利用构造函数分析极值点
极值点问题是高中数学函数部分的常见问题.运用构造函数分析极值点问题时需要明确原函数与导函数之间的关系,通过求导进行合理的转化,众所周知,一些原函数通过求导往往可转化成二次函数,而二次函数的根与函数的极值点相对应,认识到这一点也就不难分析出原函数极值点个数、极值点分布以及相关参数的范围.
例2设函数f(x)=x2+mln(1+x)有两个极值点,则实数m的取值范围是( ).

分析解答该题可按照如下思路进行:两个极值点→导函数在定义域内存在不同的两根→构造函数→结合函数性质进行解答.
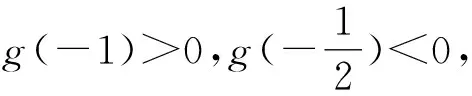
2 利用构造函数研究函数性质
研究函数的性质有两种思路:思路一,将函数转化为基本函数;思路二,构造新的函数,运用导数进行研究.高中数学中,有些题目并未给出函数的具体表达式,对于这种抽象函数,需要学生运用所学,通过认真审题,借助构造函数巧妙的切入,在此基础上借助导函数的相关性质,分析原函数的单调性、极值情况.
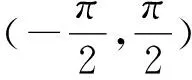
A.f(x)是增函数 B.f(x)是减函数
C.f(x)有极大值 D.f(x)有极小值
分析此题为抽象函数问题,题中没有明确的函数解析式,需要学生认真审题,对已知条件进行等价转换,运用求导的逆运算,确定原函数以及导函数的具体表达式,通过计算、比较其与零的大小关系,确定其是递增的还是递减的以及是否存在极值.
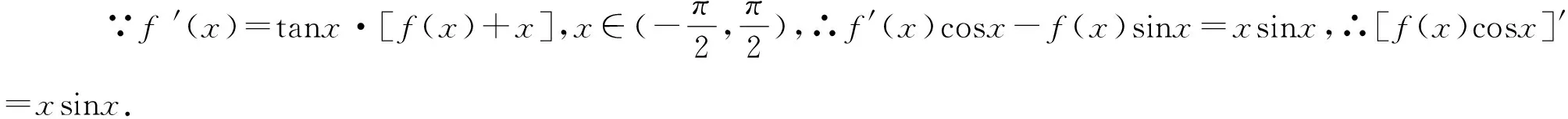

3 利用构造函数求解或证明参数范围
求解参数范围是高中数学的热门题型.不同习题的解题思路不尽相同,需要学生深入的理解给出的已知条件,通过构造新的函数化陌生为熟悉.其中对于题干中形式相同的已知条件,往往需要采用“同构”的思路进行分析.通过对已知条件进行变形,构建新的函数,通过对新函数性质的研究,得出要求解的参数范围.
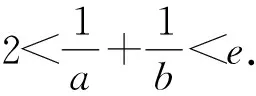
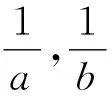

4 利用构造函数计算变量的值
计算变量的值在高中数学中较为常见.解答该类型题常常需要借助函数的单调性,因此,灵活运用多种手段正确的判断函数在定义域内的单调性是解题的关键.其中对于较为复杂的数学习题需要构建新的函数,以降低解决问题的难度.
例5 已知实数x,y满足ln(4x+3y-6)-ex+y-2≥3x+2y-6,则x+y的值为( ).
A.0 B.1 C.2 D.3
分析该题干虽然较为简单,但却是指数与对数的综合,难度较大,如思路不正确难以得出正确答案.解答该题需要对已知的条件进行变形,由不同到相同,从无形到形似,构建出两个新的函数,通过对两个新函数单调性的分析,找到两个函数特殊的点,问题便迎刃而解.
解析∵ln(4x+3y-6)-ex+y-2≥3x+2y-6,∴ln(4x+3y-6)≥ex+y-2+3x+2y-6
∴ln(4x+3y-6)-(4x+3y-6)≥ex+y-2-(x+y-2)-2
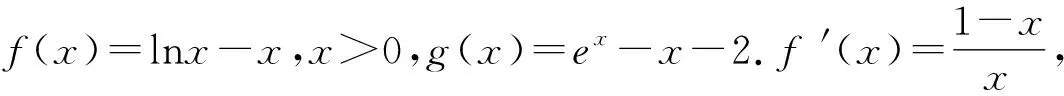
当0
g(x)min=g(0)=-1,又∵f(x)≥g(x),∴f(x)=g(x)=-1,此时4x+3y-6=1,x+y-2=0,解得x=1,y=1,则x+y=2,选择C项.
高中数学构造函数思路灵活多变,难度较大,在构建函数过程中,需要对问题仔细的分析,对函数的表达式认真的观察,明确解题的思路和方向,从而有效的解决数学问题.构造函数法是高中数学解题中的一种重要方式,教师教学中既要注重不同构造思路的讲解,也要在平时的教学过程中让学生亲身体会构造函数的具体应用过程.同时,鼓励学生做好解题的总结与反思,使其在训练中吸取经验教训,不断的提高构造函数的应用水平,使学生在提高解题能力的同时,发展其数学核心素养,从而实现综合能力的提升.

