综采工作面液压支架立柱挠度影响因素试验分析及其仿真

张浩春

山西省晋神能源有限公司 山西忻州 036599

随 着煤矿井下开采技术的不断提高和采煤装备 的不断升级换代，工作面采高的增大，工作面液压支架的支撑高度和支撑力也随之提高，因此，在液压支架构件中起着主要承载作用的液压立柱安全可靠性显得尤为重要[1]。目前，我国煤矿井下采煤工作面的最大采高已达到 8.8 m，而在采煤工作面起着支护作用的液压支架其最大支护高度也增加到了 8.8 m，同时其配套的支架立柱内径增大到 630 mm。液压支架在工作面支护顶板时，工作面顶板会对支架立柱施加轴向载荷和偏心载荷，而当立柱受到偏心载荷作用时，会产生横向挠度变化，其大小取决于立柱产生的横向挠曲量和立柱在轴向受到的载荷大小[2]。目前已有很多关于液压支架立柱方面的研究，但对于立柱在偏心载荷作用下挠度变化情况的研究不是很多，且有关支架立柱挠度计算的研究较少。笔者运用量纲分析法与仿真技术，对立柱在偏心载荷作用下挠度变化情况进行分析研究，提出一种立柱挠度值计算方法。

1 支架立柱的量纲分析

量纲分析法是在经验和试验的基础上，利用物理定律的量纲齐次原则研究确定各物理量之间的关系，此方法被广泛应用于工程和自然学科的研究中。

液压支架立柱挠度变化主要受 7 个方面的因素影响：①立柱缸体的长度l；② 立柱缸体的截面抵抗矩I；③立柱缸体材料的弹性模量E；④ 在立柱缸体内流动的乳化液运动黏度ν；⑤ 乳化液的密度ρ；⑥ 立柱缸体内的初撑力p；⑦ 偏心载荷弯矩B。

为描述上述 7 个影响因素的量纲，选取质量M、时间T和长度L这 3 个基本量为量纲，则以上 7 个因素的量纲式分别是：

(1) 缸体的长度l，其量纲 [l]=L；

(2) 立柱缸体的截面抵抗矩I，其量纲 [I]=L4；

(3) 立柱缸体的弹性模量E，其量纲 [E]=ML-1T-2；

(4) 乳化液运动黏度ν，其量纲 [ν]=ML-1T-1；

(5) 乳化液的密度ρ，其量纲 [ρ]=ML-3；

(6) 缸体内部的初撑力p，其量纲 [p]=ML-1T-2；

(7) 偏心载荷弯矩B，其量纲 [B]=ML2T-2。

立柱的挠度用y来表示，其量纲采用长度L表示。根据量纲分析理论，立柱挠度y与以上几个影响因素的关系可以用下式来表示。

式中：k为常数；幂次指数a～g为未知量。

将量纲代入式 (1)，可得

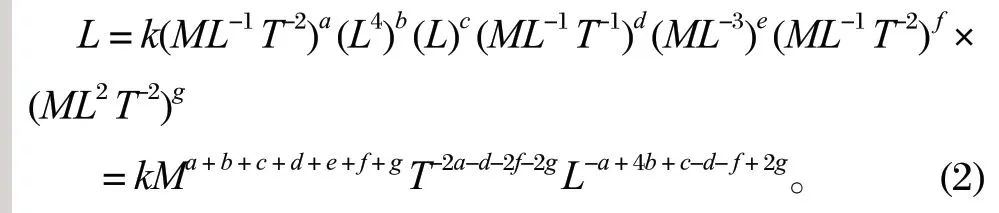
式 (2) 中，两边对应的量纲指数是相等的，即量纲M的指数为 0，量纲T的指数为 0，量纲L的指数为 1，因此可以得到

利用式 (3)～(5)，不能求解出a～g7 个未知量。因此，若将a、b、e、g4 个未知量假设成为已知量，则可以将c、d、f求解出来，得出如下结果

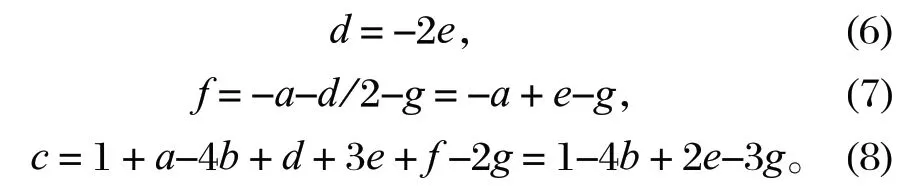
将式 (6)、(7)、(8) 代入式 (1)，可以得到支架立柱挠度量纲分析式

或

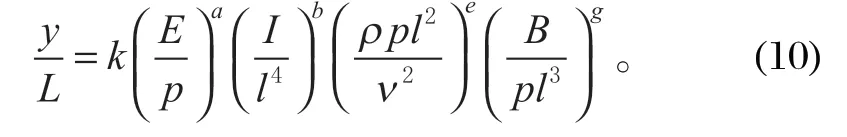
对式 (10) 两边取对数进行求导，可得

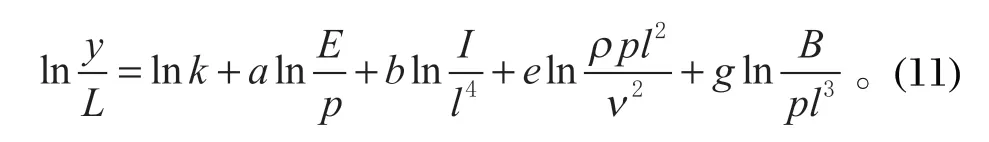
该线性方程中共有 4 个未知变量。

为求解式 (12) 中的K、a、b、e、g5 个未知量纲值，笔者选取 3 种缸径，分别为φ230、φ250 和φ500 mm 的双伸缩立柱来开展数值仿真试验，将仿真结果代入式 (12)，并运用多元线性回归方法进行分析，从而求出K、a、b、e、g5 个未知量。

2 立柱的有限元数值仿真

笔者联合运用有限单元法 (FEM) 和光滑粒子流体动力学 (SPH) 仿真技术，对支架立柱在受到偏心载荷后挠度变化情况进行仿真。

FEM 主要运用于固体域中的求解，SPH 主要运用于流体域的求解[3]。为便于解决乳化液与支柱缸体之间的流固耦合问题，笔者采用 SPH 将支柱缸体内使用的乳化液用赋予与乳化液相同物理量的质点来表示。

2.1 立柱的有限元三维模型

双伸缩液压立柱主要由缸体、导向套和活柱等部件构成。在计算支架立柱挠度时，应按照立柱全部伸出达到最大高度计算。立柱缸体中的乳化液视作 SPH 光滑粒子。双伸缩液压立柱达到最大伸出长度时的有限元模型如图 1 所示。3 种规格立柱的主要结构特征参数如表 1 所列。

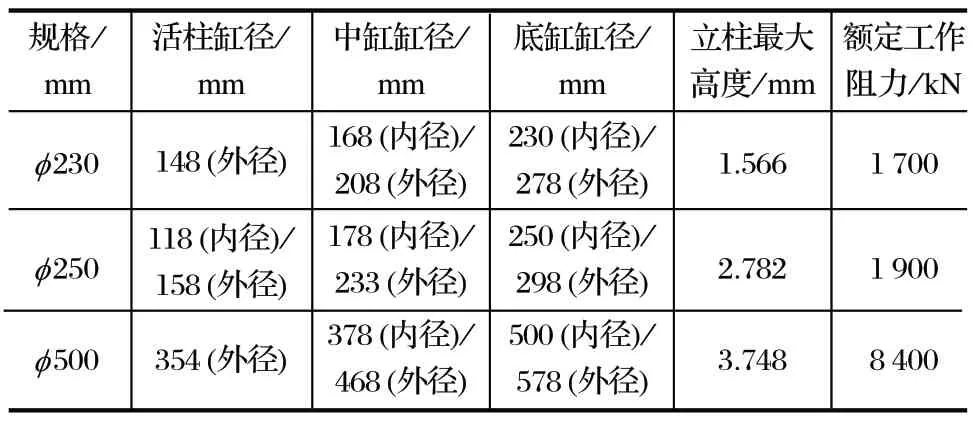
表1 3 种规格立柱主要结构特征参数Tab.1 Main structural feature parameters of three sizes of column

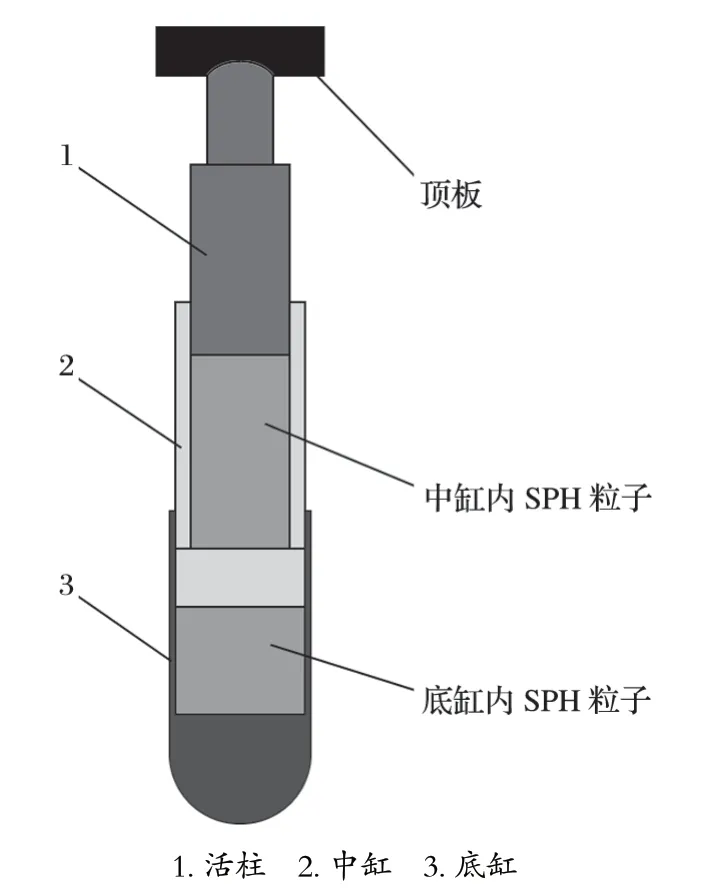
图1 立柱达到最大伸出长度时的有限元模型Fig.1 Finite element model of column while it reaching maximum length

立柱缸体的主要材料为 30CrMnSiA 合金结构钢，立柱导向套的主要材料为 42CrMo 超高强度钢，30CrMnSiA 和 42CrMo 的密度、弹性模量、泊松比均相同，分别为 7 850 kg/m3、207 GPa 和 0.3。

2.2 立柱仿真约束条件

在对立柱进行数值仿真技术分析时，假设立柱工作时的初撑力与乳化液泵站所供的压力相等。为了使分析结果具有一般代表性，规格为φ500 mm 的立柱工作时乳化液泵站压力设定为 37.5 MPa，规格为φ230 和φ250 mm 的液压立柱工作时乳化液泵站的压力不低于 31.5 MPa。

按照 GB 25974.2—2010《煤矿用液压支架 第 2 部分：立柱和千斤顶技术条件》要求，在液压支架立柱顶部加载一个偏心载荷，其大小为 1.1 倍支架额定工作阻力，此时立柱的偏心距是立柱活柱顶部圆头半径的 0.3 倍。据此可知，φ230 mm 立柱的偏心载荷为 1 870 kN，偏心距为 20.5 mm；φ250 mm 立柱的偏心载荷为 2 090 kN，偏心距为 23.2 mm；φ500 mm 立柱的偏心载荷为 9 240 kN，偏心距为 41.5 mm。为了使加载在立柱顶端的偏心载荷更加精准，在立柱活柱顶部安装一个加载模块，如图 2 所示。

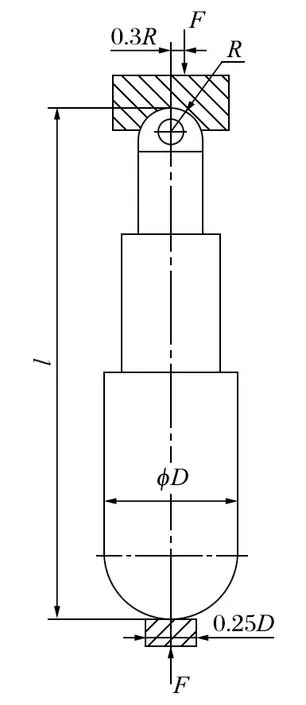
图2 立柱偏心载荷加载示意Fig.2 Sketch of eccentric load on column

约束条件：①在立柱底部缸体下端圆头外表面上的节点施加 6 个自由度的固定约束；② 在立柱活柱上部的圆头和加载模块之间、立柱导向套和立柱缸体之间均施加黏结约束；③在立柱活塞和立柱缸体内表面之间、导向套和立柱活塞杆之间施加接触约束。

2.3 立柱挠度影响因素分析

液压支架立柱的挠度受立柱的初撑力、缸体活塞与立柱缸体内壁之间的相对摩擦运动、立柱缸体变形量等因素影响[4-7]。在计算式 (12) 中的未知量时，假设立柱挠度值为已知量，同时将支架立柱划分为活柱段、中缸段和底缸段进行计算，其中各段的计算长度分别为lA、lB、lC，具体分段如图 3 所示。

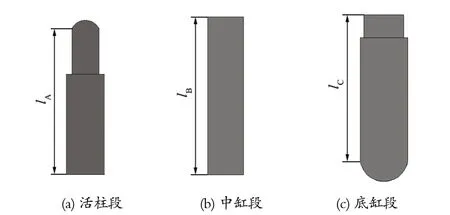
图3 立柱分段示意Fig.3 Segmented sketch of column

仿真所用 3 种规格的立柱相关参数如表 2 所列。

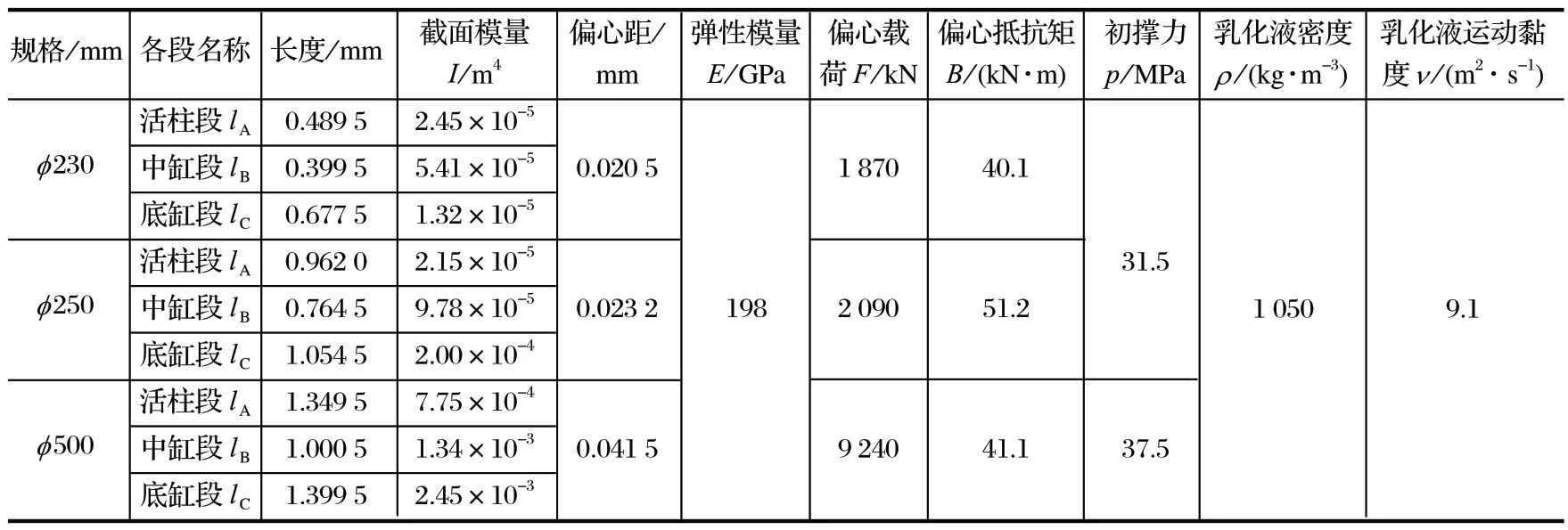
表2 3 种规格立柱各段相关参数Tab.2 Relative parameters of each segment of three sizes of column

利用上述相关条件和数值，对 3 种不同规格的支架立柱分别进行仿真，可求解得出各段挠度，如表 3 所列。

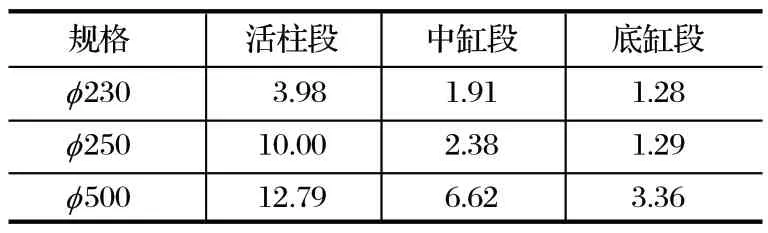
表3 3 种规格立柱各段仿真挠度Tab.3 Deflection simulations of each segment of three sizes of column mm

将以上数据代入式 (12) 中，采用多元线性回归方法进行分析计算，可得出K=-19.271，a=-0.028，b=-0.912，e=0.416，g=1.665。因K=lnk，故有k=eK=4.627×10-9。

将上述得出的数值代入到式 (9)，可得

将上述已得出的数值代入到式 (6)、(7)、(8)，可分别求解得到f=-1.219，d=-0.833，c=0.487。

根据上述计算得到所有数据如表 4 所列。

表4 各数据求解结果Tab.4 Solutions of each data

将表 4 中的各数据代入式 (1)，可得

通过式 (14)，可以分析每个因素对立柱挠度的影响。

选取初撑力p作为对立柱挠度影响因素进行研究分析，把其他参数设成不变量，初撑力由p变至p1，同时对应的立柱挠度由y变至y1，则由式 (14) 可得

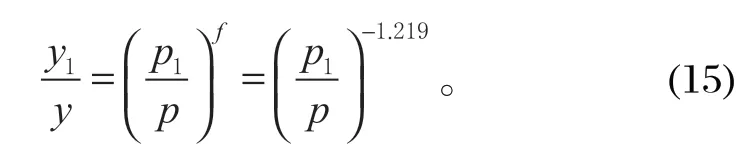
同理，可得出其他几个因素对立柱挠度的影响情况，

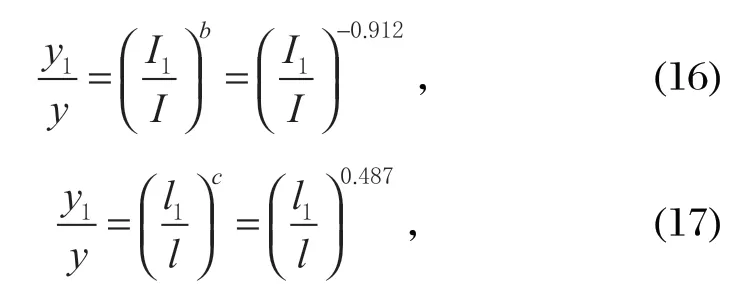
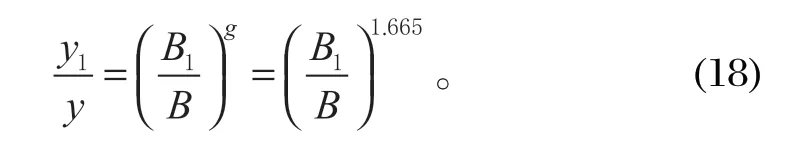
根据式 (15)～(18) 计算结果，可得立柱的挠度比值与参数之间的关系，如图 4 所示。

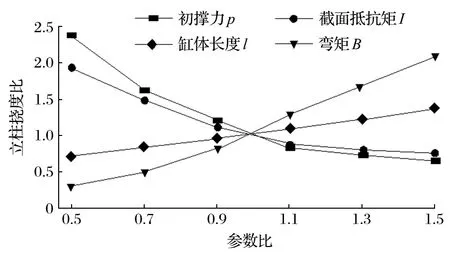
图4 立柱的挠度比与参数比之间的关系Fig.4 Relationship between deflection ratio and parameter ratio of column

由图 4 可以看出，当支柱初撑力p和截面抵抗矩I逐渐增大时，其对应的立柱挠度比值逐渐减小，而当立柱的长度l和弯矩B逐渐增大时，其对应的立柱挠度比值也随之逐渐增大。其中，支柱初撑力p和弯矩B的引起的变化率最大。由此可知，当加大支架立柱的初撑力时，等于增加了支架立柱的抗弯刚度。

在仿真模拟过程中，上述几个参数往往是同时发生变化，因此，可以把B、p、l和I这 4 个参数看作同时发生变化，变化后得到的变量值为B′、p′、l′和I′，由式 (14) 可以得到

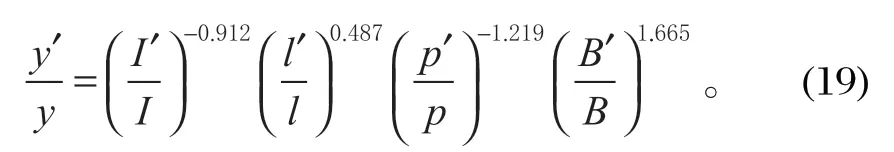
根据式 (19)，可以分析研究立柱挠度与上述参数之间的关系。

假定在其他参数不变的情况下，增加支架的初撑力和工作阻力，同时将它们提升 10%，将数值代入到式 (19)，可以求解出立柱的挠度比值为 1.039，说明立柱的挠度增加了 3.9%。当只将立柱的工作阻力增加 10% 时，立柱挠度则增加了 16.8%。因此，在实际应用过程中，提高支架立柱的初撑力，可以大大减小工作阻力增加时对立柱挠度的影响。

3 量纲分析式的有效性检验

为了检验式 (14) 的有效性，先运用该式将上述 3 种不同缸径立柱的挠度求解出来，然后任意选取一根不同缸径的立柱，假设缸径为φ400 mm，其结构参数如表 5 所列，采用式 (14) 对该立柱的挠度求解并进行仿真计算。最后将以上 4 种不同缸径立柱的量纲值、仿真值进行对比分析研究，结果如表 6 所列。

表5 φ400 mm 缸径立柱各段相关参数Tab.5 Relative parameters of each segment of φ400 mm cylinder column

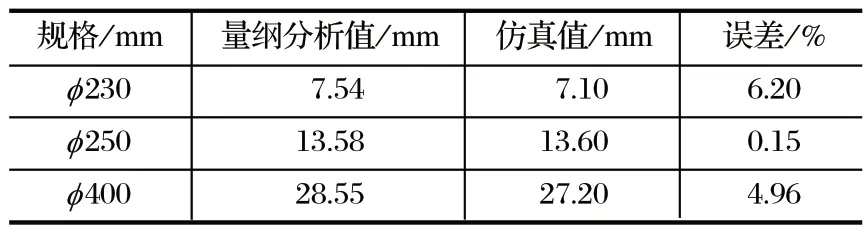
表6 不同规格立柱挠度的量纲分析值与仿真值对比Tab.6 Comparison of dimensional analysis results and simulation ones of deflection of various column

由表 6 可知，采用量纲分析得到的数值与采用仿真技术得到的数值最大误差约为 6%，两者吻合比较好。因此，立柱挠度值可以采用式 (14) 进行预估。

4 结语

通过运用量纲分析法和仿真模拟技术，建立了立柱挠度与影响其数值的几个因素之间的无量纲关系式，并得到了计算立柱挠度的公式。根据公式可知，增加支架初撑力和立柱截面抵抗矩，可以降低立柱挠度，而加大立柱弯矩和缸体长度时，立柱挠度随之增大。初撑力和立柱弯矩的变化对立柱挠度的影响最大，而立柱缸体的长度和截面模量变化对挠度值影响相对较小。在实际应用过程中，提高支架立柱的初撑力，可以大大减小工作阻力增加对立柱挠度变化的影响。