2021年全国乙卷理科第21题探析与思考

⦿满洲里远方中学 王 彬 金 铭

1 引言

2021年全国乙卷理科数学第21题是“切点弦”，“直曲联立”，“点到直线距离”，“二次函数最值”问题，题目难度中等偏上属于综合性强的题型.第一问计算出p难度较低，第二问难度中等偏上计算量较大，在实际的教学展示过程中，需要将第二问作为解析教学的重点进行展示，帮助学生找出有效解答的方法.

2 试题呈现

图1

如图1，已知抛物线C:x2=2py(p>0)的焦点F，且F与圆M:x2+(y+4)2=1上点的距离的最小值为4.

(1)求p；

(2)若点P在M上，PA,PB是C的两条切线，A,B是切点，求△PAB面积的最大值.

3 解法探析

3.1 第二小题的常用解法及评析

由于涉及切点问题，常见思路如下思维导图(图2),并以此探究第二小题的几种思路：第一是通性通法,设点的坐标，求切点弦所在直线，联立抛物线方程转化成含参的一元二次方程，求出弦长再利用点到直线距离公式求出三角形高最后求出最大面积；第二种是设直线方程与抛物线联立方程，利用韦达定理求出弦长，利用切线方程求两条切线公共点的坐标，再利用点到直线距离公式求出三角形面积最大值.

图2

3.2 通性通法

思路1用如下思维导图(图 3)来表示：

图3

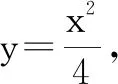
设点A(x1,y1),B(x2,y2),P(x0,y0).

x1x-2y1-2y=0.

同理，直线PB的方程为x2x-2y2-2y=0.

由于点P为直线PA，PB的公共点，则

所以，直线AB的方程x0x-2y-2y0=0.

x2-2x0x+4y0=0.

由韦达定理，可得x1+x2=2x0,x1x2=4y0.

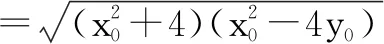
Δ=16(k2+b)>0,

又x1+x2=4k,x1x2=-4b,所以

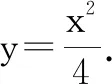
则P(2k,-b).

因为点P在M上，所以4k2+(4-b)2=1,于是-1≤4-b≤1,即3≤b≤5，则

4k2+4b=-b2+12b-15=-(b-6)2+21≤-(5-6)2+21=20.

所以，当b=5时(4k2+4b)取得最大值，此时满足k2+b>0,所以

在解法1求值过程中计算量大，解法2则要求学生掌握二次函数求最值问题，因此考虑学生知识掌握的程度要降低此题难度，给出解法3和解法4.

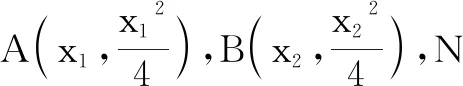
图4

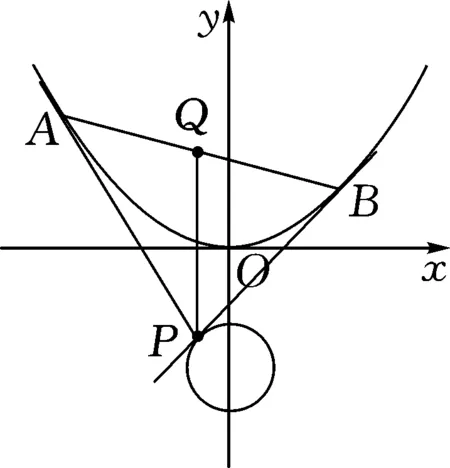
图5

由Δ=0知，16k2-4×1×(4ka-4b)=0⟹k2-ak+b=0.

设直线PA,PB的斜率分别为k1,k2.

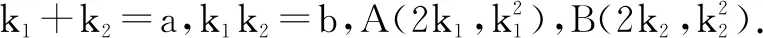
所以AB方程为

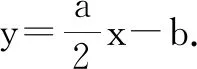
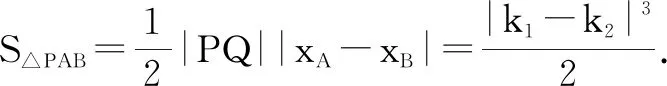
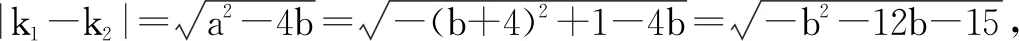
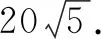
评析：此法虽然运用学生所掌握的参数法，但在求弦长时运算量仍然很大，多数学生在计算过程中可能出现错误.

3.2 秒杀法

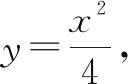
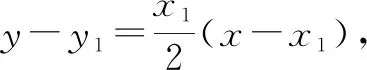
x1x-2y1-2y=0.

同理，直线PB的方程为x2x-2y2-2y=0.

所以同构lAB:mx=2(y+n).

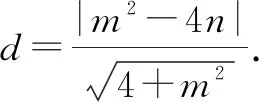
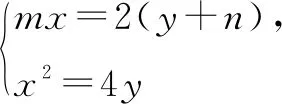
所以

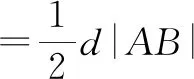
因为P在圆上，所以m2+(n+4)2=1，即m2=1-(n+4)2,所以

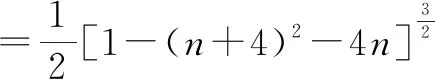
评析：由圆锥曲线切线切点弦理论的解题思路，通过简单的运算、推理找到问题的正确答案，达到减缩思维过程、降低推算难度的目的.

4 总结

本题在知识点方面考查圆与抛物线的方程、性质及三角形面积的最值，具有一定的难度，在学生能力考查上则指向逻辑推理及数学运算的核心素养.其中逻辑推理的考查体现在抛物线、直线方程的求解和三角形面积最大值的确定上，而数学运算则主要体现在第二问.学生在该题目的解答过程中需要注意的关键点为P在圆上，其横坐标与纵坐标的范围有着一定的限制.若这一点被忽视，就很容易出现解答错误.教师在教学也需要强调，在解析几何中求与动点或动直线有关的三角形面积最值，一般需要先把面积表示为某个变量的函数，再利用函数性质或均值不等式求最值.Z