数形结合改变视角 多元变量主元思想
——2021年天津导数题解法研究
⦿天津市宁河区芦台第一中学 张振山
1 引言
导数是联系高等数学与初等数学的纽带,是学习微积分的基础.导数定量地刻画了函数的局部变化,是研究函数性质的基本工具.在高考试题中,导数的考查知识十分广泛,通常考查函数的几何意义、函数的极值、单调性,并结合不等式、数列、三角函数等知识进行综合考查.通过这些知识的考查,进而考查学生的数学抽象、数学运算、直观想象和逻辑推理的数学核心素养.本文中就2021年天津高考导数题解答方法和基本数学思想加以研究.
2 题目呈现
题目(2021年天津高考第20题)已知函数f(x)=ax-xex(a>0).
(Ⅰ)求f(x)在点(0,f(0))处的切线方程;
(Ⅱ)证明f(x)存在唯一的极值点;
(Ⅲ)若存在a,使f(x)≤a+b对任意x∈R成立,求b的取值范围.
3 题目解析
第Ⅰ问略,第(Ⅱ)、(Ⅲ)问分别分析及解答如下.
3.1 第(Ⅱ)问分析及解答
分析:要证明f(x)存在唯一的极值点,即证f′(x)=a-(x+1)ex有且仅有一个零点,且在该零点的左右f′(x)的函数值符号相反.由于a是正数,于是当x<-1时,f′(x)>0.那么唯一的零点一定在区间(-1,+∞)内,只要证明f′(x)在(-1,+∞)上有唯一的零点即可.证明零点存在有两个思路:一是利用零点存在定理;二是通过画出相关函数的图象,观察交点是否存在.相应思维导图如图1所示,下面结合本思维导图给出2种解题思路6种具体证明方法.
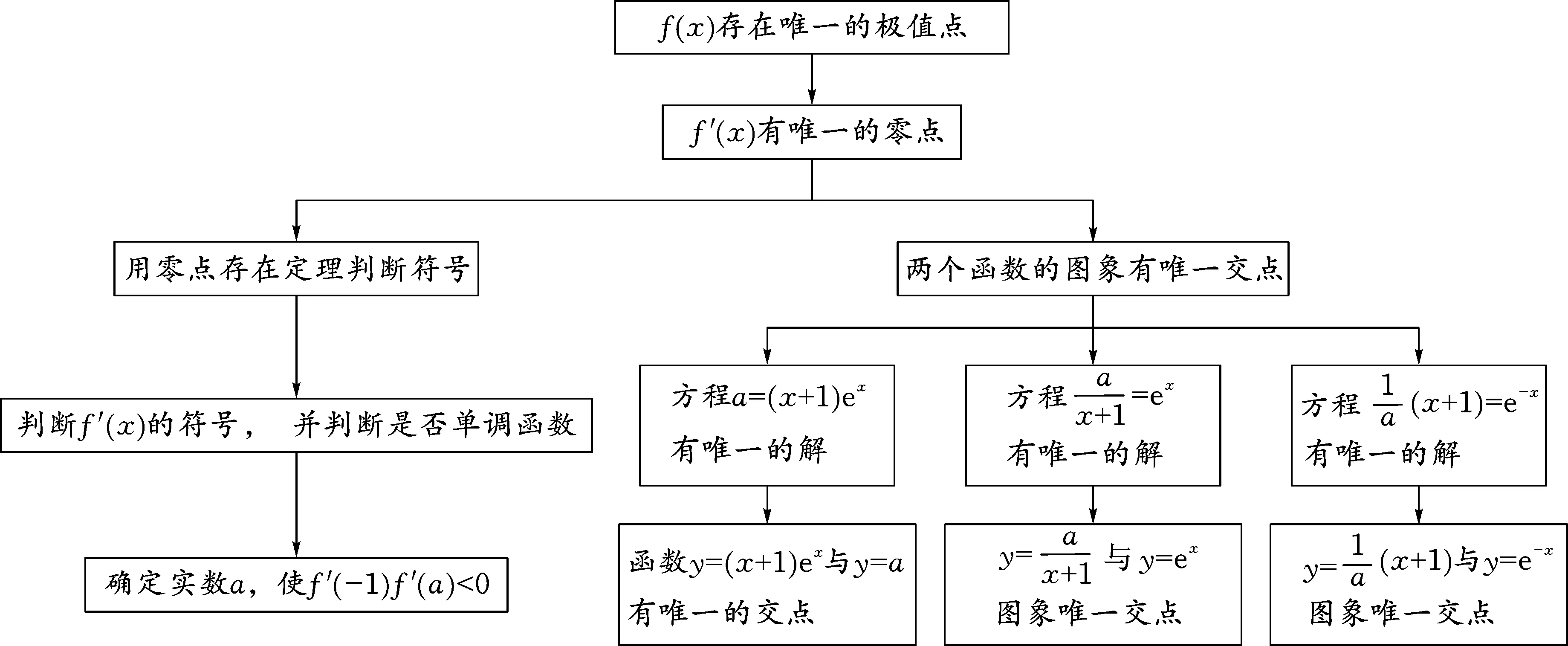
图1
解答思路1:利用零点存在定理,确定隐零点.
证法1:函数f(x)的导数f′(x)=a-ex-xex=a-(x+1)ex,f″(x)=-(x+2)ex.
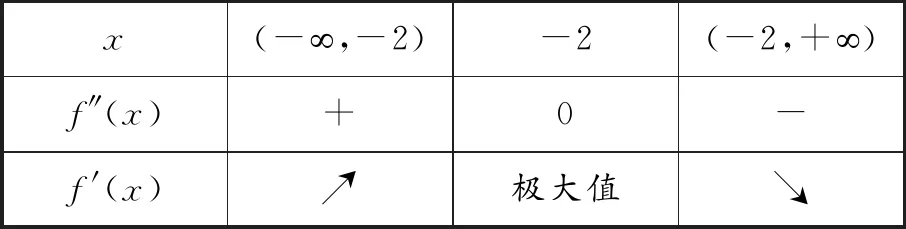
x(-朠,-2)-2(-2,+朠)f″(x)+0-f'(x)↗极大值↘
当x<-1时,(x+1)ex<0,又a>0,所以f′(x)>0.
又f′(-1)=a-(-1+1)ea=a>0,f′(a)=a-(a+1)ea=a(1-ea)-ea<0,
则f′(-1)f′(a)<0.
因此∃x0∈(-1,a),使f′(x0)=0.
所以x∈(-1,x0),f′(x)>0;x∈(x0,a),f′(x)<0.
则f(x)在(-1,x0)单调递增,在(x0,a)单调递减.
因此,f(x)存在唯一的极值点x0.
证法2:先放缩ea≥a+1>a,进而消去f′(a)中的ea,将超越函数转化为二次函数.
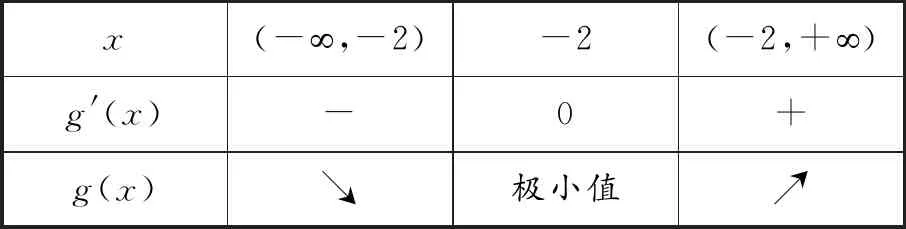
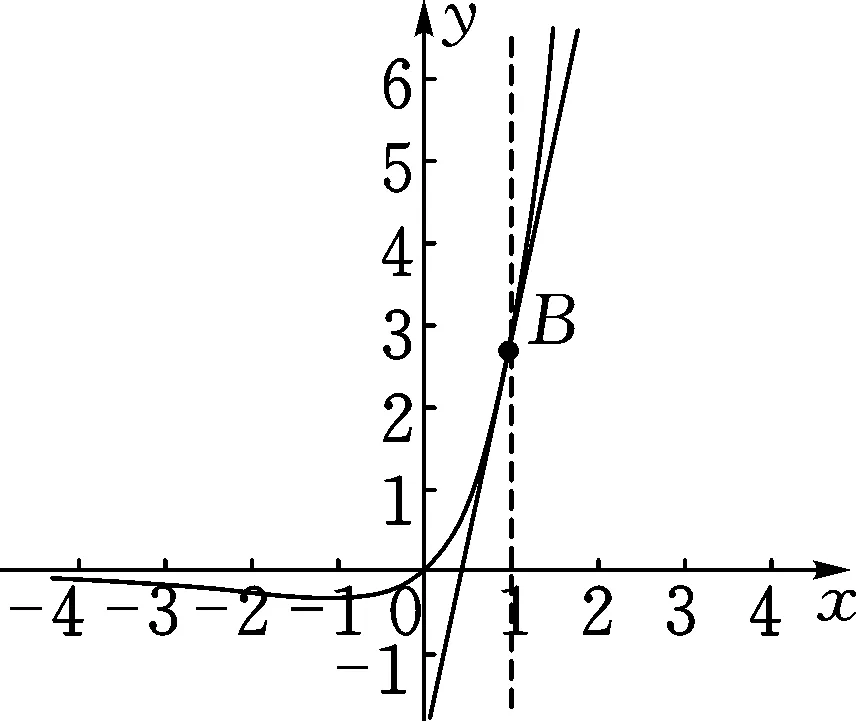
f′(a)=a-(a+1)ea 下同证法1. 证法3:将f′(x)变形,f′(x)=a-ex-xex=a-xex-ex. 令h(x)=-xex,则h′(x)=-(x+1)ex. x(-朠,-1)-1(-1,+朠)h'(x)+0-h(x)↗极大值↘ 由证法1知f′(x)在(-1,+∞)单调递减,只要确定一个实数m,使f′(m)<0即可. 下同证法1. 解答思路2:构造函数,使图象存在唯一交点. 证法4(秒杀法1):将f′(x)=a-(x+1)ex的零点等价转化. f′(x)=a-(x+1)ex有唯一零点⟺方程a=(x+1)ex有唯一的解⟺函数y=(x+1)ex的图象与y=a(a>0)有唯一的交点. 令g(x)=(x+1)ex,则g′(x)=(x+2)ex. x(-朠,-2)-2(-2,+朠)g'(x)-0+g(x)↘极小值↗ 图2 又g(-1)=0,观察图象(如图2),显然函数y=(x+1)ex的图象与y=a(a>0)有唯一的交点. 证法5(秒杀法2):由a>0及a=(x+1)ex,可判断x>-1.将a=(x+1)ex等价转化: 图3 即x0是f(x)唯一的极值点. 图4 归纳总结:对f(x)求导得f′(x)=a-(x+1)ex,即证f′(x)有且仅有一个变号零点.思路1的证明比较严谨,先判断单调函数,再寻找两个异号的函数值,进而得到零点所在位置;而思路2虽然能形象直观观察出存在唯一零点,但表述不严谨,一般在证明时不建议使用. 分析:对于多元含参不等式恒(能)成立问题,要抓住两个关键词,即“多元”“恒(能)成立”.对“多元变量”的出现,可以通过消元减少变量,也可以将某一变量当作主元,其余变量为常数,采取逐一突破的办法来实现;对于“恒(能)成立”问题,要优先考虑将参数分离.思维导图如图5所示,下面结合本思维导图给出4种解题思路5种具体解法. 图5 思路1:确定主元. 解法1:以x为主元,视为x的超越函数. f(x)≤a+b恒成立⟺f(x)max≤a+b,下面研究f(x)的最大值. 由第(Ⅱ)问可知,f(x)在(-∞,x0)单调递增,在(x0,+∞)单调递减. 所以f(x)max=f(x0)=ax0-x0ex0.于是 将a=(x0+1)ex0代入①式,整理得 因为a>0,所以(x0+1)ex0>0,即x0>-1. 令h(x)=ex(x2-x-1)(x>-1).则h′(x)=ex(x2+x-2)=ex(x+2)(x-1). x(-1,1)1(1,+朠)h'(x)-0+h(x)↘极小值↗ 所以h(x)min=h(1)=e1(1-1-1)=-e. 因为存在实数a,使f(x)≤a+b恒成立, 所以b≥-e. 解法2:以a为主元,视为a一次函数. ∀x∈R,∃a>0,使得f(x)≤a+b⟺ax-xex-a≤b⟺(x-1)a-xex-b≤0. 将a视为主元,则转化为关于a的一元一次不等式,令m(a)=(x-1)a-xex-b. 当x>1时,m(a)在(0,+∞)单调递增,则m(0)=(x-1)×0-xex-b=-xex-b<0,即b>-xex(x>1).因为φ(x)=-xex在(1,+∞)单调递减,所以φ(x)<φ(1)=-e,故b≥-e. 当x=1时,m(a)为常函数,则-e-b≤0,故b≥-e. 当x<1时,∃a>0,m(a)=(x-1)a-xex-b≤0,即(x-1)a-xex≤b. 令u(x)=(x2-x-1)ex+e,则u′(x)=(x2+x-2)ex=(x+2)(x-1)×ex<0. 所以u(x)在(-∞,1)单调递减,u(x)>u(1)=0. 于是存在a=2e,使不等式(x-1)a-xex<-e成立. 故当b≥-e时(x-1)a-xex≤b成立. 思路2:寻求必要条件,再检验. 解法2中,当x<1时并没有求b的取值范围,而是在b≥-e这个必要条件下,加已验证即可.按此思路,得出以下方法. 解法3:由于x具有任意性,先取x=1,得b≥-e. 由第(Ⅱ)问知,当a=2e时,f′(x)=a-(x+1)ex有唯一的零点1,即f(x)有唯一的极值点x0=1,且f(x)≤f(1)=e.因此只要b≥-e,则存在a=2e使得f(x)≤f(1)=e≤a+b对任意x∈R成立. 思路3:参数分离. (1)将不等式中变量b分离. 若存在实数a,使f(x)≤a+b恒成立,即b≥f(x)-a恒成立. 令g(x)=f(x)-a(a>0),则g′(x)=f′(x)=a-ex(x+1). 则[g(x)]max=[f(x)]max-a=f(x0)-a=ax0-x0ex0-a=a(x0-1)-x0ex0. 下同解法1和解法2. (2)将不等式中变量a分离. 若存在实数a,使f(x)≤a+b恒成立,即xex+b≥a(x-1)恒成立. 当x=1时,则e+b≥0,故b≥-e. 综上,b≥-e. 思路4:构造切线不等式. 受第(Ⅰ)问的启发,将y=xex与该曲线某点处的切线结合起来,把超越不等式恒成立问题转化为多项式不等式恒成立问题. 解法5:∀x∈R,∃a>0,使得f(x)≤a+b⟺ax-xex-a≤b⟺xex-ax+a+b≥0. 令h(x)=xex-ax+a+b=(xex-2ex+e)+(2e-a)(x-1)+b+e. 因为xex-2ex+e≥0,当且仅当x=1时取等号, 所以(2e-a)(x-1)+b+e≥0恒成立即可. 当b+e≥0时,即b≥-e,∃a=2e对∀x∈R,都有h(x)=xex-ax+a+b≥0,满足题意. 当b+e<0时,即b<-e,有h(1)=e+b<0,不合题意. 所以b≥-e. 图6 这里对于任意x∈R,xex≥a(x-1)-b恒成立,从几何图形分析,函数y=xex的图形不会在直线y=a(x-1)-b的下方.考察y=xex在x=1时的切线(如图6): 函数思想贯穿于整个高中数学之中,本题通过运用函数知识、函数思想、函数方法解决问题.题目对数学知识的迁移、组合、融会的程度,显示出学生个体理性思维的广度和深度.试题的解答方法灵活多变,多问设置由易到难,多角度多层次考查.试题兼顾基础性、综合性,突出对数学抽象、逻辑推理、直观想象、数学运算等数学核心素养的考查.Z
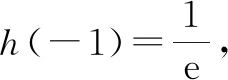
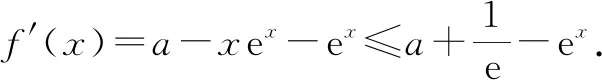
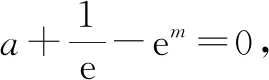
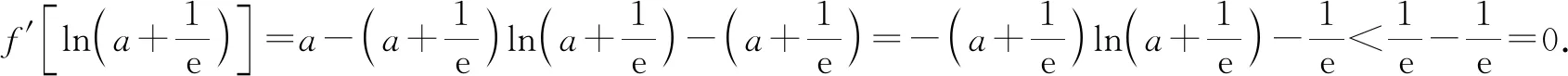

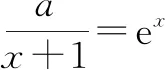

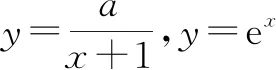
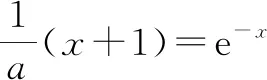
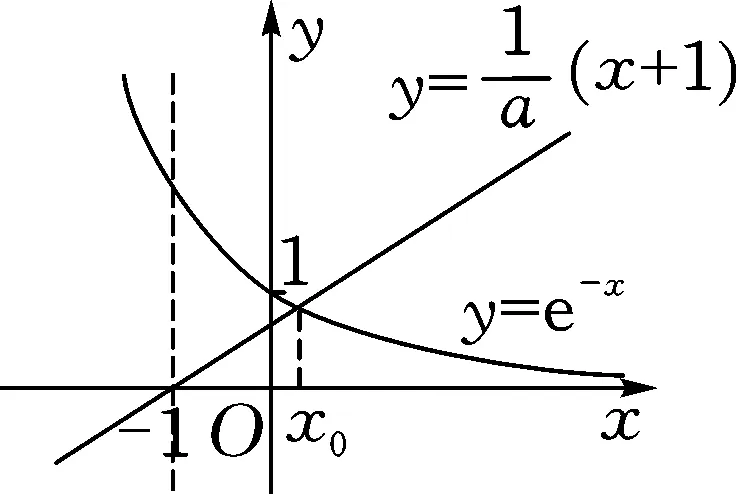
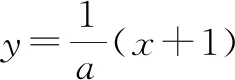
3.2 第(Ⅲ)问分析及解答
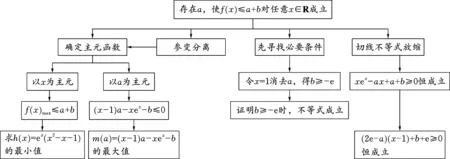

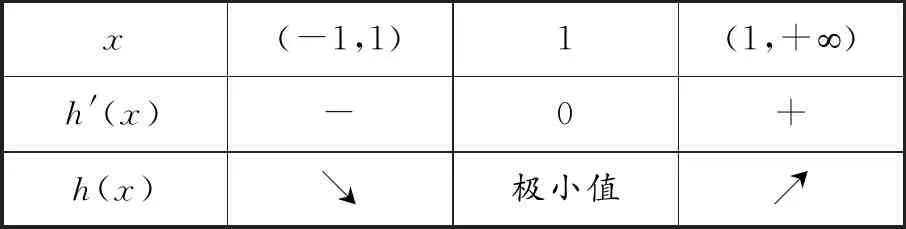
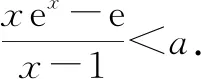
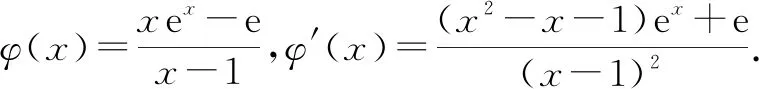
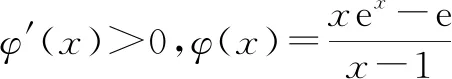
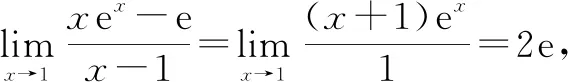

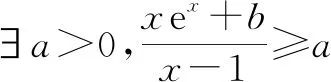
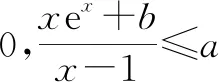
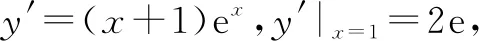
4 总结

