基于理解性学习视角下高中生态课堂构建——以“双曲线的概念”教学为例

⦿江苏省常熟市浒浦高级中学 苏 燕

1 引言

理解性学习是以“理解数学”为目标指向，引领学生迁移和运用先前知识和学习经验，在新的课堂情境中对所学内容进行有效加工，并不断获得相关知识本质的深刻理解和核心素养发展的过程[1].相比其他教学理论，理解性学习更加注重师生以及外在环境间的有机整合.而生态课堂的构建是以实现理解性学习为内涵的学习过程[2]，而且，高中某一具体数学知识都有一个结构，而这个结构能够提供相关知识潜在的简约性，从而达到理解相关本质的目的.因此，在高中生态课堂构建中，如果将学生经验性的理解逐渐上升为形式化理解，最终达到结构化理解的程度，则就能实现对这个具体知识所在内在意义的真正理解.

2 立足经验性理解，重温旧理解图式

经验性理解通常发生在学习的初始阶段，主要包括学习经验和生活经验，其中前者主要是指学生已有的数学思想、数学方法以及数学知识等等，后者主要是指学生自己对日常生活、客观对象的认知与感悟.在以理解性学习为内涵的生态课堂构建中，教师应根据学生原有的知识状况和旧理解图式，不断引导学生分析“自身经验”，有效展现与此相关知识的起始性理解.

以“双曲线的概念”教学为例，在向学生呈现双曲线“自然”的定义教学之前，分析学生的“自身经验”，再根据历届学生易出现的问题障碍点设计了如下问题串进行引导和启发.

(1)教材上是如何引导学生绘制椭圆图象的？

设计意图：明晰椭圆是应用椭圆的几何性质绘制出来的，进而为双曲线图象的绘制提供可以借鉴的途径.

(2)圆锥曲线有哪几种，椭圆是如何定义的？

设计意图：通过回顾切割圆锥模型的场景，引发学生对椭圆、双曲线等“同源性”的思考，并通过回顾椭圆的定义过程，引导学生将椭圆学习过程中的经验自然迁移到双曲线概念学习过程之中.

(3)椭圆的定义中涉及到了哪些几何元素？

设计意图：通过分析椭圆定义中的几何要素，进而类比椭圆的定义方式，有效解决没有能力直接绘制双曲线的问题.

(4)椭圆就是平面内到两定点距离之和等于定长(大于两定点间的距离)的点的轨迹，能否对其进行改造？

设计意图：由“和”猜想出“差”是比较自然的思维过程，在此前提下进行几何画板展示和动手操作，则能进一步引导学生发现双曲线概念的本质，进而获得双曲线的定义.

值得说明的是，经验化理解是最为低层的理解，往往具有易错、模糊、不确定的特点，并且，还常常包含有较多的个人经验成分.例如，由“和”联想到“差”肯定有着一定的运气成分.所以，在高中生态课堂构建中，教师还需要将经验化理解上升到形式化理解，逐步引导学生发现双曲线概念的本质.

3 注重形式化理解，构建知识获得路径

形式化理解实质上是要求学生重新整理、组织、概括和表征自身知识经验，从而达到深刻认识形式化语言和符号的目的.在以理解性学习为内涵的生态课堂构建中，教师应以生为本，充分发挥学生的主观能动性，鼓励学生通过数学实验等方式发现未知的事物及其规律，并用数学语言表述自己的再创造性思维，有效深化形式化理解的层次.

以双曲线的概念教学为例，在形式化理解环节，教师应创设如下类似实验，要求学生以小组的形式再发现、再创造.

实验1：如图1所示，在一张正方形的白纸上画一个圆F1,并在圆F1上任取一点P1，在圆F1之外任取一个定点F2，然后对折纸片使得F2与P1重合，获得一条折痕，再选取圆F1之上的其他点P2,使得点F2与P2重合，从而获得另一条折痕，重复上述操作直至获得较多的折痕，最后连接这些折痕，如图2所示，并观察所形成的图形.

图1

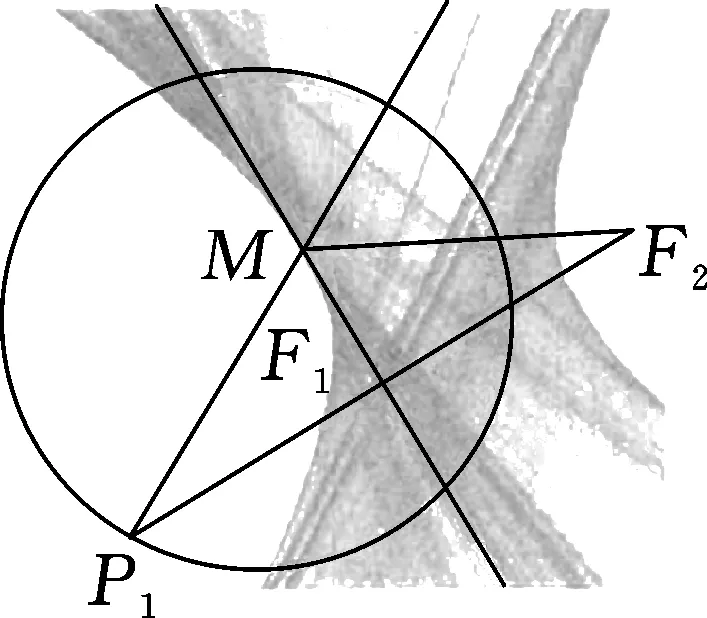
图2

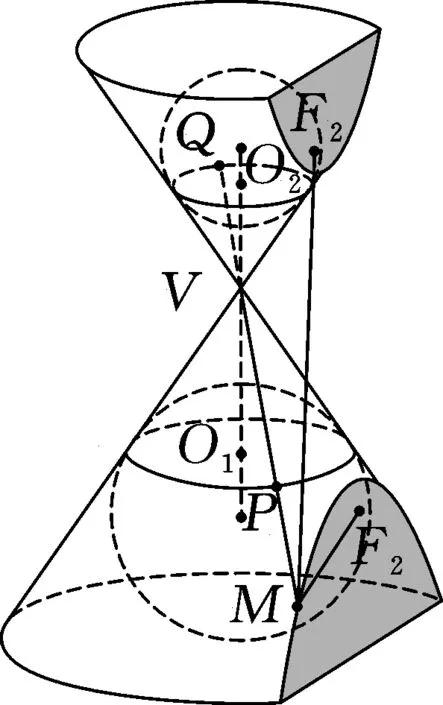
图3 旦德林双球模型

实验2：描述旦德林双球模型，如图3所示，并通过实验演示的方式引导学生得出旦德林双球模型中PF′-PF=PM-PQ=QM,其中QM为定值.

设计意图：折纸游戏的实践，以及旦德林双球模型的呈现，不仅激发了学生学习的兴趣，也深化了学生对双曲线定义的形式化理解，有效将抽象的知识具体化，进而帮助学生获得对圆锥曲线定义的统一认知.

值得一提的是，尽管形式化理解在理解层次上有了很大进步，但无法精准地揭示出该定义的外延，并在其相关知识本质理解的精细化、关联性以及丰富性等方面仍有不足.因此，在生态课堂构建中，教师还应将形式化的理解进一步转化为结构化理解，以实现相关知识所在内在意义的真正理解.

4 聚焦结构化理解，揭示外延结构体系

结构化理解意味着要在一种知识的关系脉络中有效把握相关知识的本质与内涵，在一定程度上可以认为是一种结构关联性理解，但这种理解往往需要学生自己去赋予相关的意义.因此，在以理解性学习为内涵的生态课堂构建中，教师应通过变式训练，进一步揭示具体知识所蕴含的丰富的外延体系结构[3]，最后自然生成新的理解，并在新旧理解之间构建实质性的联系.

以双曲线的概念教学为例，在学习该概念之前，学生就已经认知到了反比例函数的图象也是双曲线，但对于该双曲线与本节课程所要学习到的圆锥曲线所对应的双曲线两者之间是否存在联系，许多学生不能准确地给出相应的答案.因此，教师可以以该问题为契机，引导学生从双曲线标准方程的结构中进行解答.

同时，为了进一步深化学生对双曲线概念的认识，促使学生经历从形式到结构的飞跃，教师还应按照差异性、层次性、多元化的原则，呈现如下函数，要求判断该函数图象是否是双曲线，若是双曲线，则要求说出它的渐近线，并试着描绘出相应的图象.

(3)x2+xy-2y2+3y-4=0.

5 结论

总之，基于理解性学习视角下的高中生态课堂构建并不是以高层次的思维代替低层次的思维，而是要求以较低层次的思维作为高层次思维发展的前提和基础，也就是说在具体教学实践中教师要不断促进和带动低层次思维向高层次发展，有效将学生的经验性理解上升为结构化理解[4].因此，基于理解性学习视角下的高中生态课堂构建是自我完善、自我发展、自我建构的过程，这也正是理解性学习理论的核心所在.