用研讨学教法讲新高考原题*

⦿海南昌江中学 廖明艳 林瑞记

1 引言

在2021年高考结束之后，很多老师都在感叹：“今年的高考题怎一个‘新’字了得！”无论是试题命制的创新度、效度或是区分度，都达到了很高的标准，特别是创新度，很好地考查了学生运用数学知识来解决实际问题的综合能力，达到了高考的选拔性功能和目的.在新高考原题的启发下，我们要应用适当的讲解方法，积极引导学生深度思考和剖析试题，从通法到秒杀，由点及面地把握新高考的脉络.

2 先通法后秒杀

2.1 2021年全国新高考Ⅱ卷第12题

2.1.1 题目及分析

设正整数n=a0·20+a1·21+…+ak-1·2k-1+ak·2k,其中ai∈{0,1}(i=0,1,2,…,k),记ω(n)=a0+a1+…+ak，则( ).

A.ω(2n)=ω(n) B.ω(2n+3)=ω(n)+1

C.ω(8n+5)=ω(4n+3) D.ω(2n-1)=n

试题分析：考生可以先观察表达式n=a0·20+a1·21+…+ak-1·2k-1+ak·2k的特点，ω(n)=a0+a1+…+ak实际上是每项2n(n=1,2,3,…,k)前的系数和，并结合选项做适当的变换，得出表达式中的系数和，即可自然而然地得出正确答案.其思维导图如图1.

图1

实际上，在基数b的位置记数系统(其中b是一个正自然数，叫做基数)，b个基本符号(或者叫数字)对应于包括0的最小b个自然数.要产生其他的数，符号在数中的位置要被用到.最后一位的符号用它本身的值，向左一位其值乘以b.一般来讲，若b是基底，我们在b进制系统中的数表示为a0·b0+a1·b1+…+ak-1·bk-1+ak·bk的形式，并按次序写下数字a0a1…ak-1ak.这些数字是0到b-1的自然数.

一般来讲，b进制系统中的数有如下形式：

数bk和b-k是相应数字的比重.

2.1.2 具体解答

通法1：因为2n=0·20+a0·21+a1·22+…+ak-1·2k+ak·2k+1，所以有ω(2n)=0+a0+a1+…+ak-1+ak=ω(n)，故A答案正确；

当n=2时，2n+3=7=1·20+1·21+1·22，所以ω(7)=3，又2=0·20+1·21，所以有ω(2)=0+1=1，于是有ω(7)≠ω(2)+1，故B选项错误；

因为8n+5=a0·23+a1·24+…+ak-1·2k+2+ak·2k+3+5=1·20+0·21+1·22+a0·23+a1·24+…+ak-1·2k+2+ak·2k+3，

所以ω(8n+5)=a0+a1+…+ak+2，又4n+3=a0·22+a1·23+…+ak-1·2k+1+ak·2k+2+3=1·20+1·21+a0·22+a1·23+…+ak-1·2k+1+ak·2k+2，所以ω(4n+3)=a0+a1+…+ak+2=ω(8n+5)，故C选项正确；

因为2n-1=1·20+1·21+1·22+…+1·2n-2+1·2n-1，所以ω(2n-1)=n，故D选项正确.

综上所述，故选：ACD.

通法2：根据二进制计数法则可知，任何正整数n=(akak-1…a1a0)2，均可用二进制加权系数的形式表示.如5=(101)2=1×20+0×21+1×22，即任何正整数n都可以表示2k的多项式，ω(n)=a0+a1+…+ak表示其系数的和，理解上述这两点，则

2n=0·20+a0·21+a1·22+…+ak-1·2k

+ak·2k+1,

于是ω(2n)=0+a0+a1+…+ak-1+ak=ω(n).选项A正确；

因为2n+3=1×20+a0·21+a1·22+…+ak-1·2k+ak·2k+1+2,所以选项B不正确；

因为8n+5=1·20+0·21+1·22+a0·23+a1·24+…+ak-1·2k+2+ak·2k+3,所以ω(8n+5)=ω(n)+2,4n+3=1·20+1·21+a0·22+a1·23+…+ak-1·2k+1+ak·2k+2,所以ω(4n+3)=ω(n)+2.选项C正确；

秒杀法：因为n=(akak-1…a1a0)2，则2n=(akak-1…a1a00)2，于是ω(2n)=ω(n),A正确；

2n+3=(akak-1…a1a00)2+3=(akak-1…a1a01)2+2，当a0=0,ω(2n+3)=ω(n)+2,所以B不正确；

8n+5=(akak-1…a1a0000)2+1·22+0·21+1·20=(akak-1…a1a0101)2，4n+3=(akak-1…a1a000)2+1·21+1·20=(akak-1…a1a011)2，所以C正确；

教学启示：2021年作为海南新高考的第二年考了这么一道题，实属意料之外，又确在情理之中，如醍醐灌顶般给了我们中学一线教师很多启发.倘若在教学中只停留于课本教常规的知识点已很难满足现实的需求，一昧的灌输也很难适应现在的考题，这也不符合新课改提倡的培养学生学科核心素养的要求.授人鱼更要授人以渔，在对这一类型题目的讲解教学过程中，研讨式教学法可以很好地发挥作用，便于培养学生的发散性思维，举一隅以三隅，立足于学生的发展，有利于学生构建自己的知识框架，将学到的数学知识提炼出思想并内化为能力，这于学生的终身发展至关重要.

2.2 2021年全国新高考Ⅱ卷第16题

2.2.1 题目

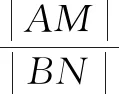
2.2.2 思维导图

其解法的思维导图如图2所示.

图2

2.2.3 具体解答

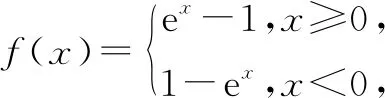
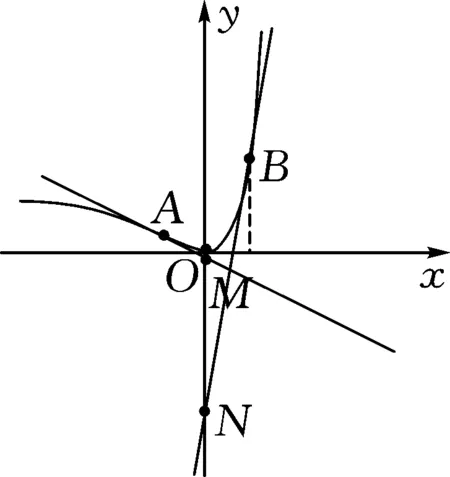
图3

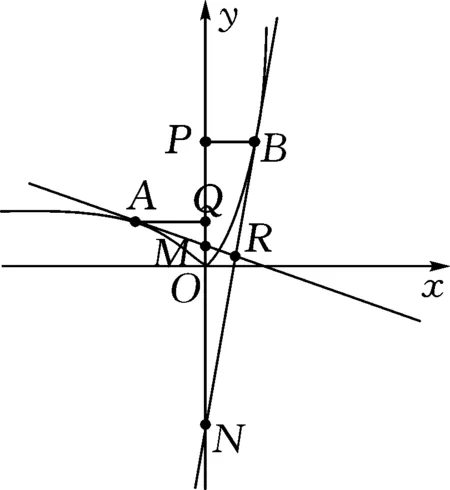
图4

秒杀法：如图4，因为两条切线相互垂直，有kAM×kBN=-ex1ex2=-ex1+x2=-1⟹x1+x2=0⟹x1=-x2.过A,B两点分别做y轴的垂线，垂足分别为Q,P，于是有AQ=PB，∠ARN=∠NPB，且有∠NMR=∠NBP，又有对顶角∠NMR=∠AMQ，故△AMQ∽△NBP.

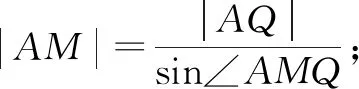
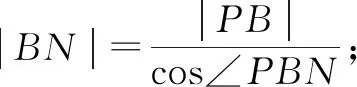
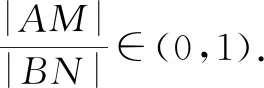
3 总结

虽然数学解题方法千变万化，但是方法只有繁简之分而无好坏之别，毕竟条条大路通罗马.在日常的课堂教学中往往复杂的解法能获得意料不到的效果，能做到有效地锻炼学生的数学运算能力，能很好地培养学生的学科核心素养，这对学生获得扎实的运算能力助益良多，甚至会启发学生思索出更加简洁且有创造性的方法.新课改提倡教师角色应当由“教书匠”转化为“研究者”，由“指导者”转化为“促进者”等等.在日常的数学课堂上应用研讨学教法，于关键处启发学生，于学生于教师均收获良多，教师更应该是学生学习的合作者，不断与时俱进，化作一眼活泉，为学生涌现出更加丰富多彩的数学知识和缤纷世界.Z