返璞归真 直观想象
——立体几何中的截面问题
⦿安徽省临泉田家炳实验中学 于飞洋
1 引言
用一个平面(或不共线的三点、两平行直线等)去截空间几何体,此平面与空间几何体的交集叫做这个空间几何体的截面.涉及立体几何中空间几何体的截面问题,沟通“二维”与“三维”之间的联系,链接起空间几何体中点、直线、平面等要素“动”与“静”之间的联系,实现“平面”与“立体”之间的转化,是历年高考数学试卷中比较常见的热点问题之一,创新新颖,应用性强,备受关注.
2 截面问题探究
2.1 截面作图
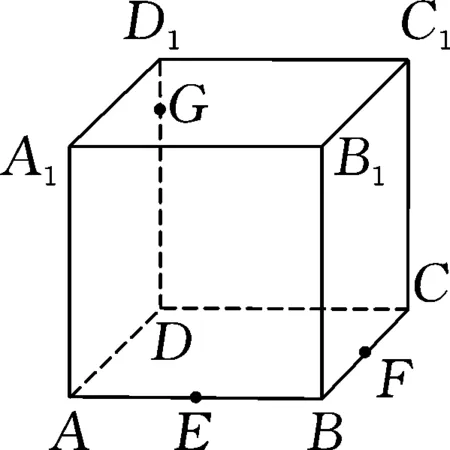
图1
例1如图1,在正方体ABCD-A1B1C1D1中,E,F,G分别在AB,BC,DD1上,求作过E,F,G三点的截面.
分析:从底面ABCD入手,确定直线EF与两个侧面AA1D1D和DD1C1C的交点情况,再通过连接相应的交点与点G的连线,进一步确定相应直线在正方体中的交点情况,从而得到对应的截面.

图2
作法:如图2,①在底面ABCD内,过E,F作直线EF,分别与DA,DC的延长线交于L,M;
②在侧面AA1D1D内,连接LG交AA1于K;
③在侧面DD1C1C内,连接GM交CC1于H;
④连接KE,FH,则五边形EFHGK即为所求的截面.
点评:此类涉及空间几何体的截面作图问题,破解的关键就是要“心中有图”,要求学生要有比较强的空间想象能力,结合对应的条件加以数形结合,直观想象.空间几何体的截面作图也为立体几何中的其他截面问题的分析与处理提供理论基础与条件.
2.2 截面判断
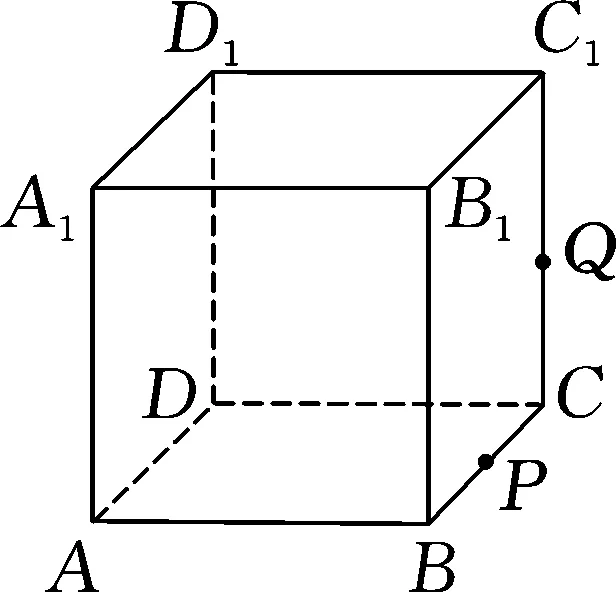
图3
例2(多选题)如图3,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是( ).
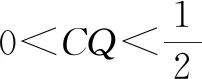
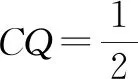
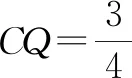
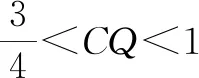
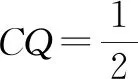
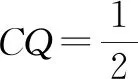
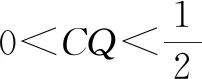
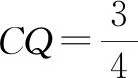
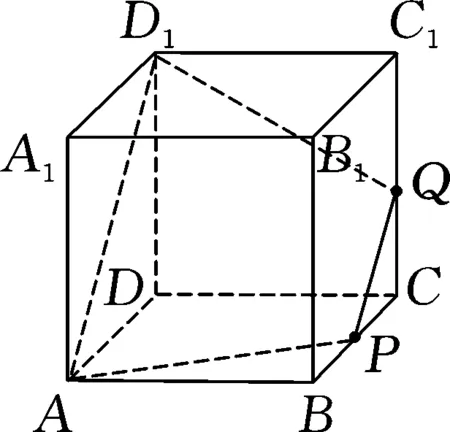
图4
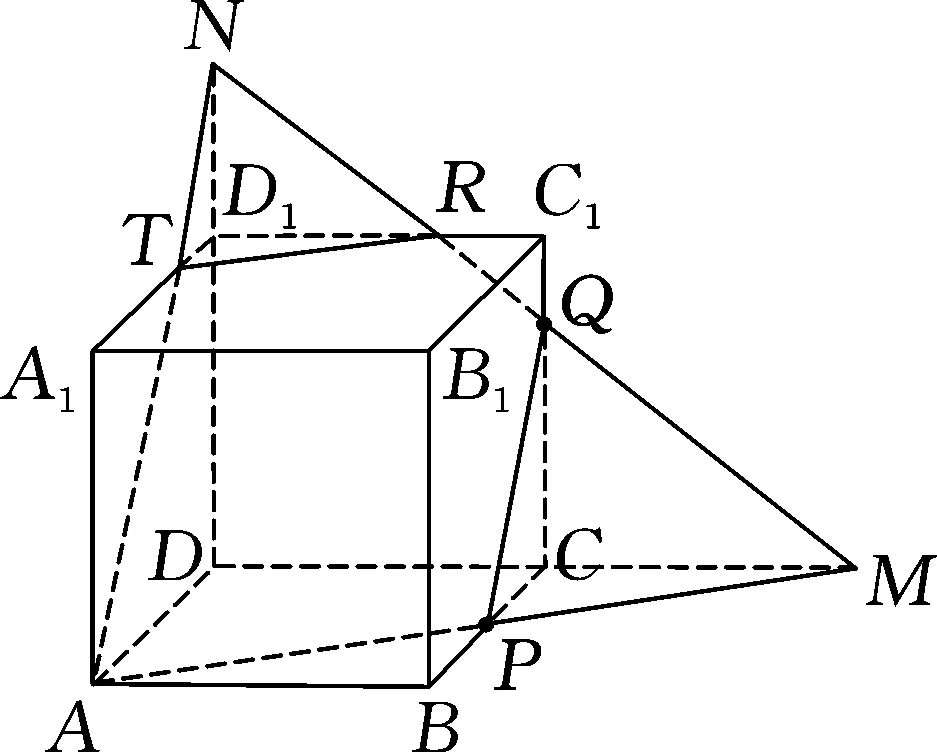
图5
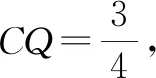
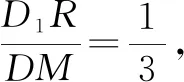
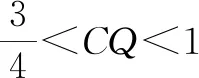
故选择答案:ABC.
点评:此类涉及空间几何体的截面形状以及相关几何性质的判断问题,破解的关键是利用条件作出对应的截面图形,综合线面位置关系的判定与性质加以分析与推理,同时数形结合,直观想象,合理确定截面几何图形所满足的特征性质,得以确定相应的截面图形的形状或几何性质等.
2.3 截面面积
例3已知正三棱柱ABC-A1B1C1的侧棱长为4,底面边长为2,用一个平面截此棱柱,与侧棱AA1,BB1,CC1分别交于点M,N,Q,若△MNQ为直角三角形,则△MNQ面积的最小值为( ).
分析:通过引入参数设出相应的边,结合正三棱柱的特征以及直角三角形的性质,找到相关边之间的等量关系式,借助三角形面积公式加以代数转化得到相应的关系式,利用代数关系式的特征,直接利用二次函数的图象与性质来分析.
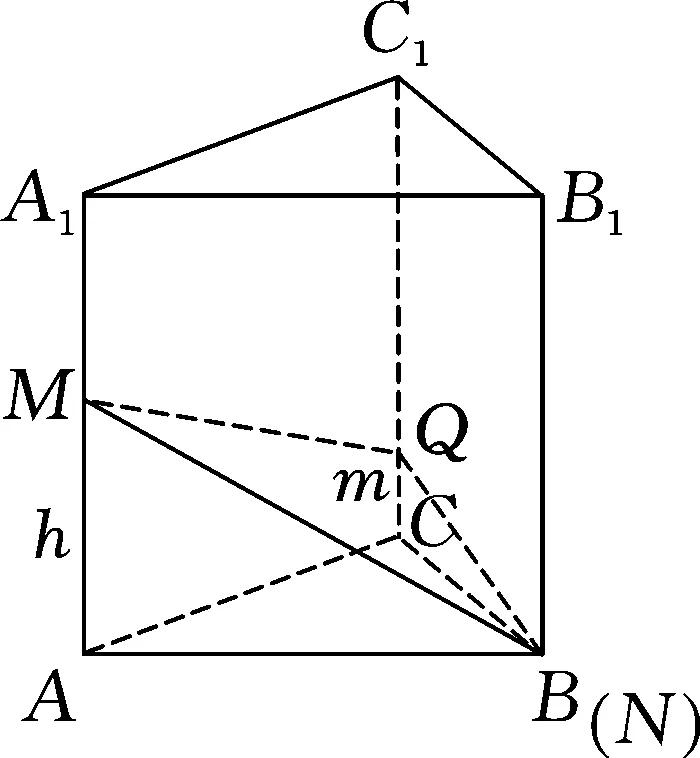
图6
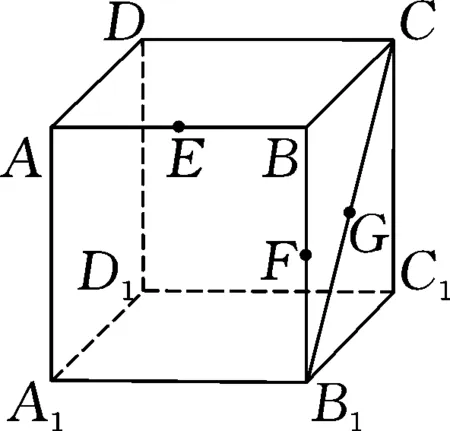
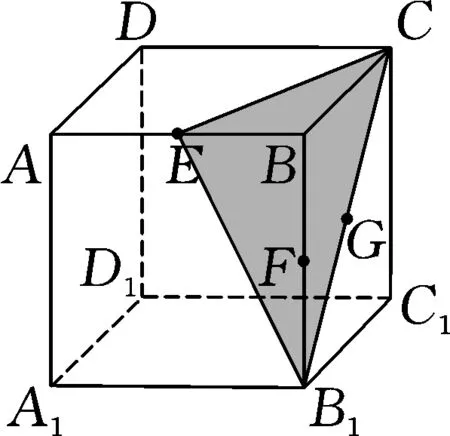
解析:如图6所示,不妨设点N在点B处,设|AM|=h,|CQ|=m,不失一般性,设0 则有|MN|2=h2+4,|NQ|2=m2+4,|MQ|2=(h-m)2+4. 结合判别式Δ=h2-8≥0,则有h2≥8,且h≤4,即 8≤h2≤16. =1+h2. 因为8≤h2≤16,所以S2=1+h2∈[9,17]. 故选择答案:A. 点评:此类涉及空间几何体的截面所对应的面积最值问题,破解时一方面可以“动”中取“静”,确定极端情况时动点的位置,利用直观想象与数形结合加以分析与处理;一方面可以引入参数(或角参或边参),结合条件构建截面所对应的面积关系式,利用函数的图象与性质加以分析与处理. 例4如图7所示,有一容积为1立方单位的正方体容器ABCD-A1B1C1D1,若在棱AB,BB1及对角线B1C的中点各有一小孔E,F,G,且此容器可以任意放置,则该容器可装水的最大容积是( ). 图7 图8 分析:先通过过E,B1,G三点的截面来确定对应的三棱锥,并求解此时三棱锥的体积,结合空间几何体的性质分析此时即为满足条件的该容器可装水的最大容积,进而得以求解最大容积问题. 故选择答案:C. 点评:此类涉及空间几何体的截面分隔开来的几何体的体积问题,破解的关键是确定满足条件的截面以及所分隔开来的几何体所对应的边长等数量信息,综合空间几何体的体积关系或体积公式来综合应用与处理. 其实,破解涉及立体几何中空间几何体的截面问题,合理利用平面的性质确定截面形状,其中确定截面的主要依据包括:平面的四个公理及推论,直线和平面平行的判定和性质,两个平面平行的性质以及球的截面的性质等.结合平面几何图形的性质特征来分析与转化是解决相应截面问题的关键.Z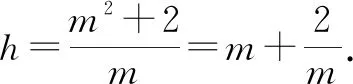
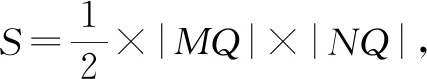
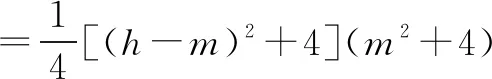
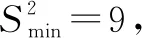
2.4 体积问题
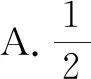
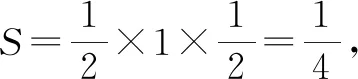
3 结语

