妙解排列组合里的涂色问题

⦿江苏省江安高级中学 肖雄伟

1 一分步，二分类

对于某些不复杂的涂色问题，使用分步计数原理处理会更加简便.如果题目所给的条件比较多的时候，此时就应该以题目的已知条件为依据，把分步计数原理和分类计数原理结合起来进行求解.在实际情况中，要牢记优先处理有特殊要求的色块.解题步骤为首先处理特殊的色块，再依据实际情况，如果附加要求多，那就先使用分步计数原理，再使用分类计数原理解答；如果是不难的涂色问题，就可以直接运用分步计数原理解题.

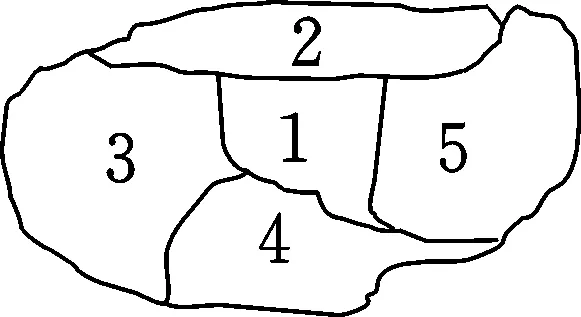
图1

例题1假设中国的某一个省由5个市区组成，这个省的市区分布如图1所示，现给地图上色，要求相邻区域使用的颜色不能相同，现有4种颜色可供选择，那么不同的上色方法一共有种.

分析：这个题目与很多题目都有相似的地方，但是图形是有变化的，因此就需要学生有较强的观察能力和分析能力.分析发现，市区1与其他市区不一样，它跟另外的四个市区都是相邻的，被其他四个市区包围着.因此在解答题目的时候，需要优先考虑分步计数的方法，即首先将市区1涂上颜色，那么市区1就有4种选择方法，再利用分类计数的方法，当市区2和市区4的颜色一样的时候，就有3种上色方法，那么总的上色方法就有4×3×2×2=48种；当市区2和市区4的颜色不一样的时候，优先给市区2上色的方法有3种，此时市区4就有两种上色方法，那么市区3和市区5就只有一种上色方法，因此此时上色的总方法数为：4×3×2×1×1=24种.所以，一共有24+48=72种上色方法.

图2

推广1如图2，用4种不同颜色给图中A，B，C，D，E，F六个点涂色，要求每个点都要涂一种颜色，且图中每条线段的两个端点涂不同的颜色，则不同的涂色方法有种.

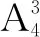
2 一分类，二分步

对于某些较为复杂繁琐的涂色问题，就需要首先以使用颜色的种类为依据进行分类，特别是不同的题目对于要求使用颜色的种类也不一样.当题目中出现要求三种颜色时就需要进行分类计数，如果没有出现最多使用三种颜色的要求，那么问题就更复杂了，还需要做深入的思考和处理，分类计数原理是处理此类复杂问题的首要方法.即解题步骤为首先分析题目要求的用色的种类，要求有最多使用三种颜色的就可以进行分类，如果没有最多三种颜色这个条件的要求，那么需要再思索.一般来说，中学阶段出现后面这种情况的题型很少.

图3

例题2

.

.

分析：分析题目信息可以知道，此题与例题1有共同的特点，就是结合使用分步和分类的方法来解题，但它明显比例题1复杂得多.因此对于此题应该首先以使用颜色的种类为依据来进行分类，这样就会简便许多，出错的几率也会相应减小.分类方式有两种：

因此，一共有30+360=390种上色方法.

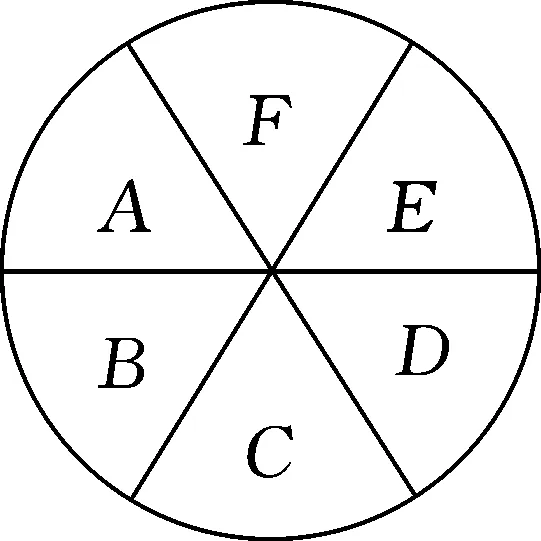
图4

推广2在一个正六边形的六个区域内栽种观赏植物，如图4，要求同一块区域内栽种同一种植物，相邻的两块区域种植不同的植物，现有4种不同的植物可供选择，则有种种植方案.

分析：对问题所给条件分析，不难发现解答该问题需要使用分类计数原理和分步计数原理.以种植植物的种类个数为依据计算，进而求解具体种植方案仍具有一定难度.应考虑局部分类法，即以不相邻区域的种植植物种类个数为分类依据，进一步计算种植方案.则该问题可以分为三类情况：

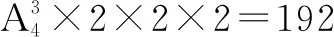
所以，一共有种植方案108+432+192=732种.

在此，通过以上对范式理论和集约相关理论的研究探讨，可将维修集约范式初步界定为：在资源优化配置和有效使用的原则下,通过综合组织、设计维修主体和维修程式，而形成的紧凑、高效、有序的维修活动组织及可持续发展模式。维修集约范式的内涵组成如图1所示。其中，维修主体是实施、管理和评价维修活动的作业单位；将维修主体开展的维修业务流程定义为维修程式，即将基于一定的维修资源,运用一定的维修策略,在一定的维修作业地点,对一定的维修对象开展的一系列维修活动。

3 一平面，二空间

对于一些很难掌握的点线面需要涂色的立体图形，由于相邻的地方比较多，因此就需要先把立体问题转化成为平面上的问题，然后再以使用颜色的种类为依据进行分类解答.即解题步骤为首先将立体图形转化成为平面图形，再根据题目情况分类，具体的分类情况由实际题目的要求决定，分类依据还是以使用的颜色种类为依据，分别进行讨论求解，最后所有情况相加就是需要求的总的情况数.

例题3已知有一个四棱锥P-ABCD，如图5所示，使用4种不同的颜色在四棱锥的每个面上上色，要求相邻的区域颜色不同，一共有多少种涂法？

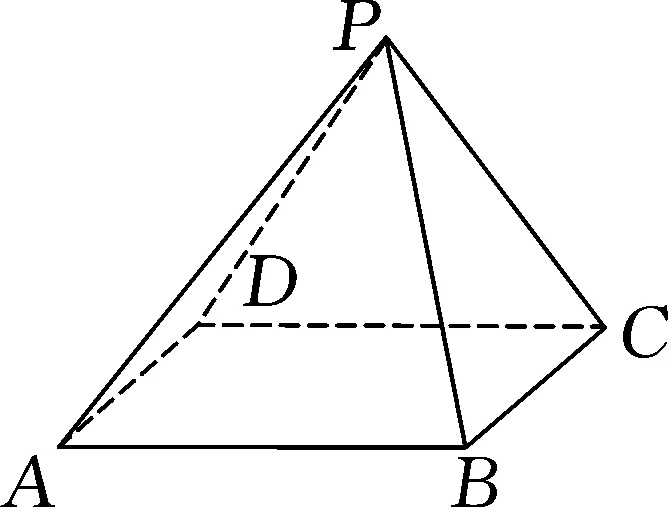
图5

图6

分析：分析可知，此题需要将立体图形转化成平面图形，在平面区域中涂色.如图6所示，区域1，2，3，4等价于四棱锥的侧面，区域5等价于底面.下面就以使用的颜色的种类来分类：

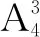
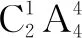
推广3用6种不同颜色给三棱柱ABC-DEF的面涂色，如图7所示，要求有公共棱的平面涂色不相同，则有多少种涂色方法?

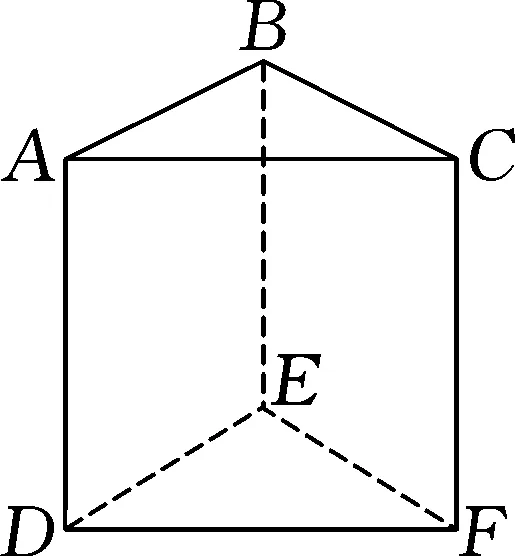
图7

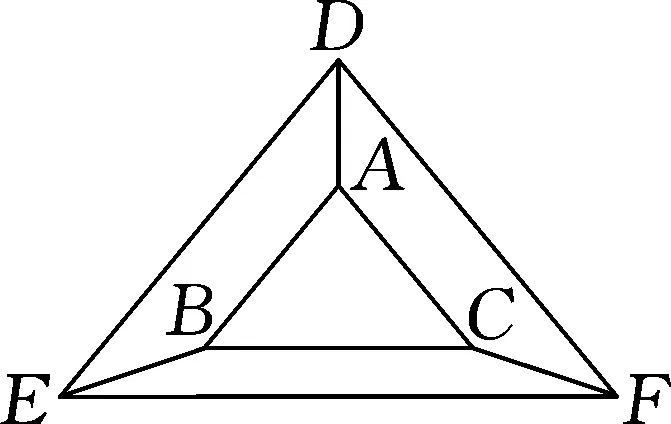
图8

分析：根据例题3可知，几何体有关于平面的涂色问题，解答时通常转化为平面图形进行求解.则该问题的求解思路与之类似，即将图7的三棱柱ABC-DEF转变为图8的平面图形，以涂色颜色的种类为依据分类进行求解，其中图7中三棱柱的底面DEF也需要涂色.由已知条件可知，至少需要上4种颜色，具体的解题过程为：

涂色方法计数问题是目前排列组合问题的重难点，要学会正确的解答思路.解决此类问题的策略，首先要分析题目，然后再根据题目选择合适的解题方法，正确使用分类和分步计数原理.对于排列组合的基础知识也需要掌握牢固，避免出现基础性的错误.