一道联赛椭圆试题的破解及拓展
⦿江苏省西亭高级中学 金 鑫
1 引言
圆锥曲线是高中数学中的基本知识之一,是高中数学联赛中常见考点之一.此类问题很好交汇代数与几何,“数”“形”融合,“动”“静”兼备,是数学多方面知识融合与交汇的一大重要场所,有效考查数学基础知识与数学关键能力,体现选拔与区分功能的主阵地之一.
2问题呈现
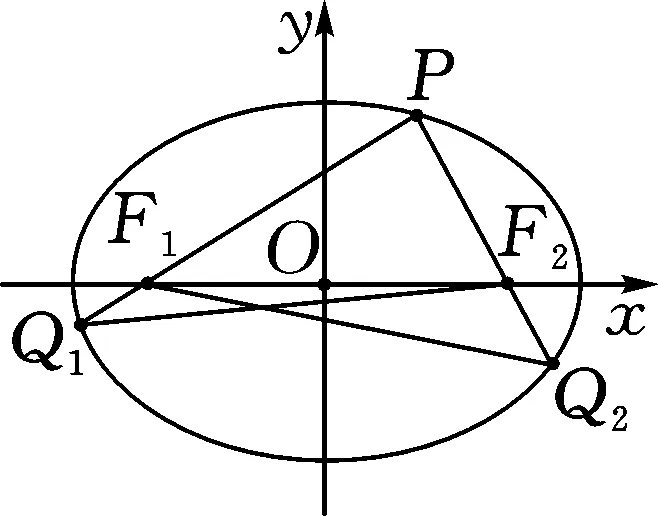
图1

此题为高中联赛一试解答题中的最后一题,难度比较大.以椭圆为问题背景,利用平面几何中对应三角形的内切圆来创设情境,结合基本不等式、三角函数等的应用来达到应用与破解的目的.
3 问题破解
方法1:官方参考答案——坐标法.
解析:易知F1(-1,0),F2(1,0),设P(x0,y0),Q1(x1,y1),Q2(x2,y2),由条件知x0,y0>0,y1<0,y2<0.
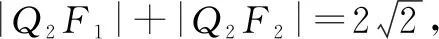





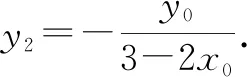


点评:根据条件设出对应点的坐标,利用椭圆的定义确定两对应三角形的周长,利用三角形的面积公式确定对应内切圆的半径,进而得到两半径差的关系式;结合直线与椭圆的方程联立,利用函数与方程思维,借助韦达定理加以转化,确定相关点的坐标之间的关系式,进而转化对应的关系式,结合基本不等式的应用,从而得以确定对应的最值问题.坐标法处理圆锥曲线问题,是破解此类问题是最常用的技巧方法之一.
方法2:单变量参数方程法.
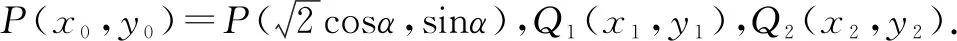
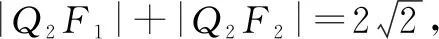
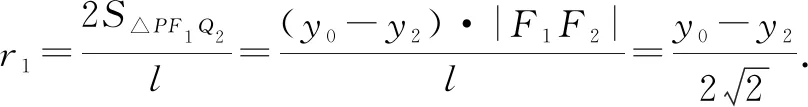



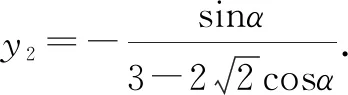


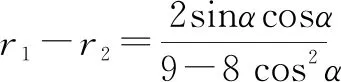
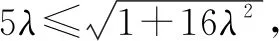
方法3:多变量参数方程法.
解析:易知F1(-1,0),F2(1,0).

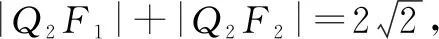
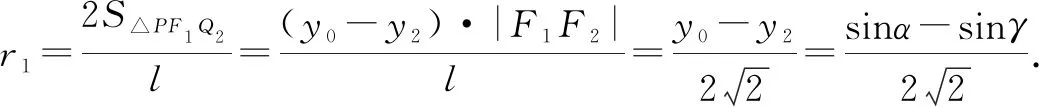
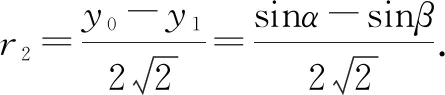
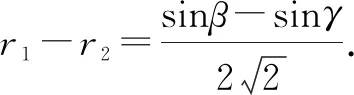

即
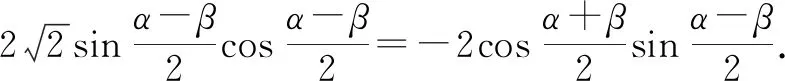

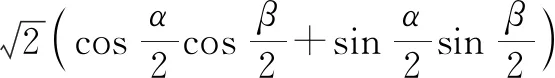

由万能公式得
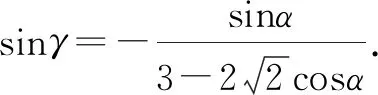
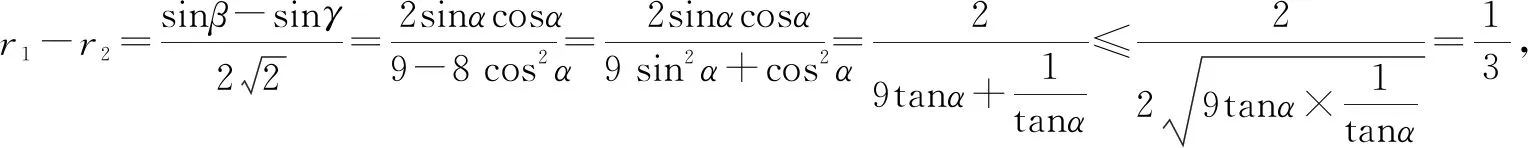

点评:根据题目条件,椭圆上的三个点引入对应的参数坐标,进而确定两对应三角形的内切圆半径之差r1-r2的三角函数关系式,结合三点共线构建三角函数关系式,并利用三角恒等变形加以转化与处理,最后再利用基本不等式来确定相应的最值问题.多参数引入,元素较多,要求具备非常好的数学运算与逻辑推理能力.
4 探究拓展
探究:保留题目创新背景,化特殊情况为一般情况,可以得到更具有一般性的普通性结论.
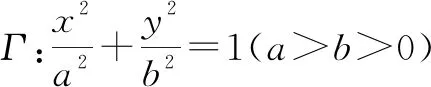
证明:易知F1(-c,0),F2(c,0).
设P(x0,y0),Q1(x1,y1),Q2(x2,y2),由条件知x0,y0>0,y1<0,y2<0.
由椭圆定义得|PF1|+|PF2|=|Q1F1|+|Q1F2|=|Q2F1|+|Q2F2|=2a,故△PF1Q2与△PF2Q1的周长均为l=4a.

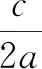






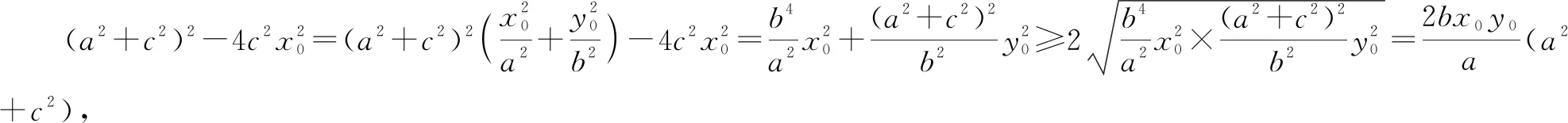
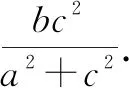

5 解后反思
涉及圆锥曲线中相关三角形的内切圆的性质及其应用,是圆锥曲线相关知识的进一步综合与应用,背景生动,创新新颖,内容丰富,综合性强,趣味规律.通过相应性质的理解与掌握,结合圆锥曲线的相关知识与基本性质加以合理转化,综合函数与方程、三角函数、不等式等其他相关的知识,巧妙处理,有效提升学生的逻辑推理能力、数学运算能力等,创新意识与创新应用,全面促进数学思维能力和思维品质的提高,增强数学关键能力,培养数学核心素养.Z

