基于深度学习的“直线与圆锥曲线位置关系”复习课微设计

⦿山东省临清市第一中学 姚继新

1 引言

直线与圆锥曲线的位置关系问题历来是高考的一个热点内容，更是一个难点内容.为了提高高三复习课的效率，笔者选择2021年4月份山东大联考试卷中的第21题作为这节课的“主打题”.该题是一道典型的直线与圆锥曲线的位置关系问题，特征明显，思路多样，于是笔者便“借题发挥”，在课堂上与学生就此展开了讨论.

2 教学过程微设计片段

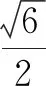
(1)求动点M的轨迹E的方程；

(2)点P为直线x=3上一动点，过P点作曲线E的切线，切点为Q，线段PQ的中点为N，问是否存在定点T，满足|PQ|=2|NT|？若存在，求出定点T的坐标；若不存在，请说明理由.

感想1：本题是这次联考试卷的倒数第二题，按惯常的思维考虑，应属于“难解”的大题范畴，甚至被有些考生“战略性放弃”的题目.但就如高考的“解析几何解答题”一样，近几年呈现出“难度下降”的特点，不再那么高不可攀，考生“攻克此题”亦从不可能变为可能.

感想2：本题从出题的角度及形式看，属于常规套路.第一问是常见的“求轨迹方程”，属于“白送分”.第二问要求考生就定点T的存在性进行探索，这种设计相较很多题目让考生直接“求定点T的坐标”的设计增加了迷惑性，对考生有明显的思维上的干扰(毕竟考生还并不是非常确定“定点T”就一定存在)，考查学生的数学探究能力，符合当前考查学生学科核心素养的命题导向.

生1：根据直线与椭圆的位置关系常用方法，联立方程组，根据相切关系可以设点依次求解.

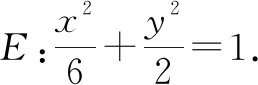
(2)由题意可知直线PQ的斜率一定存在，设直线PQ的方程为y=kx+m(m≠0)，Q(x0,y0).

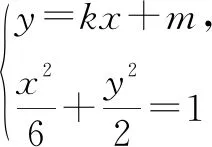
Δ=36k2m2-12(1+3k2)(m2-2)=0，

化简得

m2=2(3k2+1).

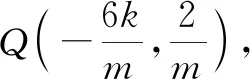
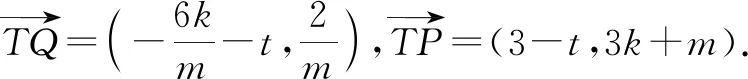
师：生1的解法非常好，是一个非常典型的解法，也可以算作是通性通法了.该方法的好处在于思路清晰，逻辑严密，便于方法的展开，但缺点也很明显，就是运算量偏大，过程稍显“繁琐”.大家再想一想，能否让过程变得更简捷？

生2：如果我们聚焦于“PQ是椭圆的切线”这个条件，则可以简化第二问的解题过程.

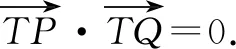
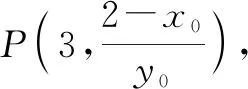
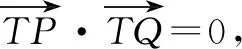
这时候，老师发现生3非常着急的样子，显然有话要说，于是示意生3也说一说.

生3：老师先前讲过“特殊化”的思想，在这里，如果我们先从特殊情况入手获得定点T，再证明该点对一般情况也适合，是不是也可以得解.

师：从特殊到一般来研究问题，快速找到突破点，这是很好的想法，大家不妨试一下.

数分钟后：

令y=0，可得x=1,或x=2.下面再检验一下一般情况.

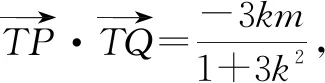
(2)若T(2,0)，此时……符合题意.

综上所述，存在定点T(2,0)满足|PQ|=2|NT|.

以上是笔者微设计的全部内容，但一路走下来，心里怪怪的，总有差那么一点的感觉，就在这时，生4同学举手示意，“老师，我还有一种想法”.

生4：老师，我发现利用椭圆的切点弦方程，本题还可以这样解.

师生不由得鼓起掌来，听到教室里面掌声响起来，刚才那种“怪怪的感觉”也烟消云散了.

3 结束语

美国数学家波利亚在《怎样解题》中说过,解题的价值不是答案的本身，而在于弄清“是怎样想到这个解法的？”、“是什么促使你这样想，这样做的？”这就是深度学习的基本特征之一:要“学透”知识，不仅知其然也要知其所以然，还要知其可能然.深度学习的另一个基本特征就是要“学活”知识，要做到活学活用，举一反三，并能够依据不同情境创造性的迁移和应用知识，灵活解决同一类型的不同问题.以上两个特征体现了深度学习“要关注知识、关注能力培养”，而深度学习的第三个基本特征则是要“参悟”知识，深度学习不止于文本，而是基于文本内容的新的生长和超越，这种生长和超越，既可以是对文本内容本身的拓展和深化，也可以是对文本内容新的思考和体悟，这第三个基本特征则是要“见人”了，在“参悟知识”过程中提升核心素养、实现“立德树人”的成长，这就是“解题教学”弥足珍贵的价值.Z