结合相似性测度与随机森林的个人信用评估模型

都珂珂， 张 玥， 赵 凯

(安徽工程大学 数理与金融学院，安徽 芜湖 241000)

0 引 言

随着大数据时代的到来，大数据技术卓越的数据采集和计算能力，使得数据信息更加完全但同时导致了数据结构变得复杂，数据处理难度也大大增加。客户信用数据项具有维度多、数量大、复杂性等问题[1]，处理起来众多且复杂。因此，通过量化和融合多视角信用信息度量客户之间的相似性是合理的，如何选择合适的度量工具是处理信用信息数据的基础。

近年来，由于机器学习和人工智能领域的快速发展，信用评估方法，特别是基于组合模型和集成学习的信用评估方法得到了广泛的应用[2-3]。Breiman[4]引入了基于个人信用评估的随机森林算法，发现所学习的集合模型精度高于任何单个模型；Harris[5]组合多支持向量机解决了非线性支持向量机的局限性，进一步拓展了模型组合的多样性；张棚[6]运用随机森林提取重要特征，并将其用于自适应模糊推理系统的输入数据，最终在UCI德国信用数据集上预测借贷人员的信用风险，分类效果良好，验证了随机森林优越的特征提取功能。组合模型方法依据应用场景的不同选择适宜的处理工具，弥补了各单一方法的局限性，是如今个人信用评估领域采用的主流研究方式。在模型组合的多样性方面，个人信用评估方法多基于弱分类器融合角度，很少有学者从相似性匹配角度来研究，这为探究新的组合方式提供了思路。基于测度的信用评估方法创新点在于能够细致地考虑不同信用数据的几何形状，多角度划分数据，并进行相似性匹配，用相对较小的相似距离度量作为评判标准，距离越小则相似性越大，二者划为同一类的偏向就越大。

假设特征空间是欧氏空间，本文针对可进行二值化转码的属性，引入Hamming 距离量化使用二进制编码产生的固定长度字符串之间的相似性[7]。针对可以数量度量的数据，本文提出使用向量空间中一致范数导出的Chebyshev距离度量，用表示向量之间角度的Cosine距离量化客户信用差异。此外，考虑到客户所携带的原始特征向量是高维的、稀疏的和冗余的，容易导致相似性匹配的性能退化，本文采用与特征提取具有高度自洽性的随机森林方法提取与信用状态密切相关的特征，从而产生重要的特征向量使得模型的准确性与稳健性同步得到提高。这样，将3个基于距离的度量分别进行相似性比较，使得个人信用风险评估结果由基于加权投票的方法融合而成。

1 研究方法与设计

不同的度量(距离度量或散度)是解决模式识别问题的有效工具，在分类、聚类和检索[8]等领域已被广泛地应用。在分析信用风险时，可以通过不同信用类别客户特征数据之间的差异来进行评估。这样，个人信用评估问题就变成了特征数据的相似性匹配问题。但是在选取3种常被用于分类的距离测度进行分类实验时，发现其分类的准确性还有很大的提升空间，分类结果如图1所示。为解决这一问题，采用投票分类的方式从多视角出发，将3种距离测度所产生的决策进行综合评估来提升模型的性能。除此之外，为了去除原始数据中冗余信息对评估准确性的干扰，从提取重要特征的需求出发，选择与这一需求具有自洽性的随机森林方法，提出了结合相似性测度与随机森林的个人信用评估模型。

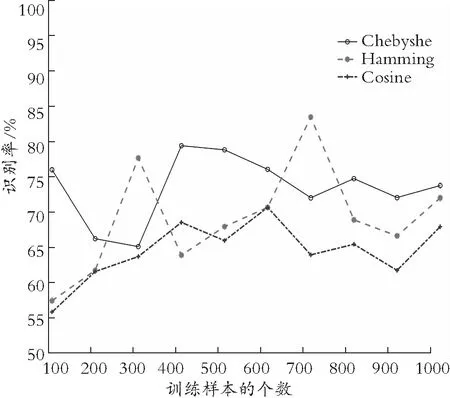
图1 原始数据集上相似性度量的性能比较

如图2所示，提出的多视角决策融合包含3个关键阶段: 重要特征的提取、基于随机森林的相似性匹配和决策融合。第一阶段运用随机森林的方法提取重要特征对原始数据进行降维；第二阶段在重要信用特征之间分别通过Hamming距离、Chebyshev距离和Cosine距离进行相似性匹配；最后阶段，通过加权投票进行多视角决策融合。在以下两节中，本文将逐步详细介绍所提出的方法。

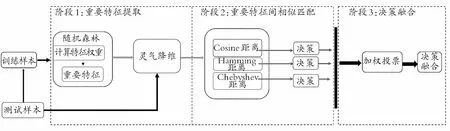
图2 模型框架

本文所涉及的Hamming距离、Chebyshev 距离与Cosine距离的具体数学表达形式在表1中罗列:

表1 3种距离度量的公式

1.1 基于随机森林的重要特征提取

原有的客户信用特征具有高维性、信息冗余性、稀疏性等特点[12]，直接使用基于距离的度量会导致风险评估方法的能力退化。为了弥补这些缺陷，采用随机森林方法，对每个特征赋予权重，然后依据权重对特征进行排列，设置权重的阈值，从训练样本中提取与信用具有强影响力的特征。进一步来说，通过重要特征提取实现了数据降维，解决冗余信息对分类的干扰，提升模型的分类效率。

1.2 基于距离的相似度匹配

在提取重要特征后，对测试样本和训练样本进行相似性匹配。为此，由3种测度对应的方程式分别计算测试样本与训练样本的重要信用特征之间的Hamming距离、Chebyshev距离和cosine距离。

1.3 多视角的决策融合

在完成上述步骤后，本文从3个方面获得了基于随机森林的决策，下一个是最终决策。在这一步中，采用加权投票补充基于度量决策的优点，并进一步提高决策的准确性，因此最终决策基于投票矩阵和决策方程产生。

2 实 验

在这一部分中，进行了几个实验来验证所提出方法的有效性。实验数据是德国信用数据集，其中每个数据点包含20个属性和类别标签，以表明在15万名贷款申请者范围内的良好信用或不良信用风险。评估任务在Matlab(Version2016a)编程环境下用Inteli5×8250u处理器在笔记本电脑上完成。

2.1 模型参数的设定

随机森林分类的准确度很大程度上受树棵数n的影响。选择过少的树棵数，会导致预测结果不理想；选择过多的树棵数，会降低分类准确率的提升效果，甚至延长计算速度、降低计算速率。本文选取100棵树，分别以MostPopular数据与ExcludingIn-bagObservation数据的袋外数据分类误差为评价指标，来探究树棵数的选取对判断准确性的影响，其结果如图3所示。

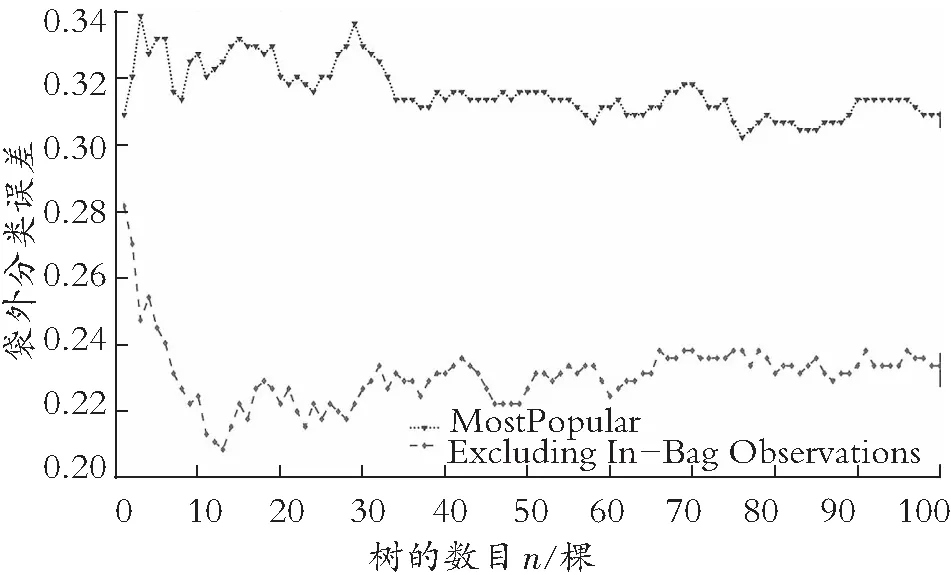
图3 两数据集的袋外分类误差变化折线图

图3中，折线图的横坐标表示树棵数，纵坐标表示模型的袋外数据分类误差率。可以看出，两条折线的转折点都在n=32左右。当n<32时，随着树数目的增多，Excluding In-bag Observations数据的错误率由28%下降到22%左右，Most Popular数据的判断错误率略有波动但差距极小；当n>32时，两组数据的错误率趋于平稳。故选择n=32作为随机森林模型树的数目。

2.2 重要特征的提取

计算单个特征变量的重要性是随机森林方法拥有的一个显著特性[13]，这使得随机森林方法与本模型所提取出的重要特征提取要求具有高度自洽性。随机森林方法比较特征变量重要性的评判标准通常采用袋外数据分类误差。这是因为生成随机决策树时采用随机有放回的方法采样，不会将所有的样本引入用于生成一棵树，这个过程使得袋外数据(OOB)得以产生。通过对比加入噪声后特征的袋外数据分类误差变化幅度来判断重要性，变化幅度越大则特征越重要。这种方法可以在模型生成过程中取得真实误差的无偏估计，且不损失训练数据量。具体的选择过程如下：

步骤1 计算每个特征的重要性；

步骤2 确定要剔除的比例，在此基础上依据特征重要性降序剔除冗余特征，得到一个新的特征集；

步骤3 用新的特征集重复上述过程，直到剩下事先设定的特征值的数目；

步骤4 对比上述过程提取的特征集的袋外误差率，选择袋外误差率最低的特征集。

使用随机森林方法，按照上述方式对特征进行权重赋值，并依据权重值对其降序排列，选取出23条评分较高的款项，其结果如图4所示。并以此图为评判依据选出重要的23个款项，对其进行属性划分后，最终提取13个重要特征，并实现数据的降维，具体属性如表2所示。

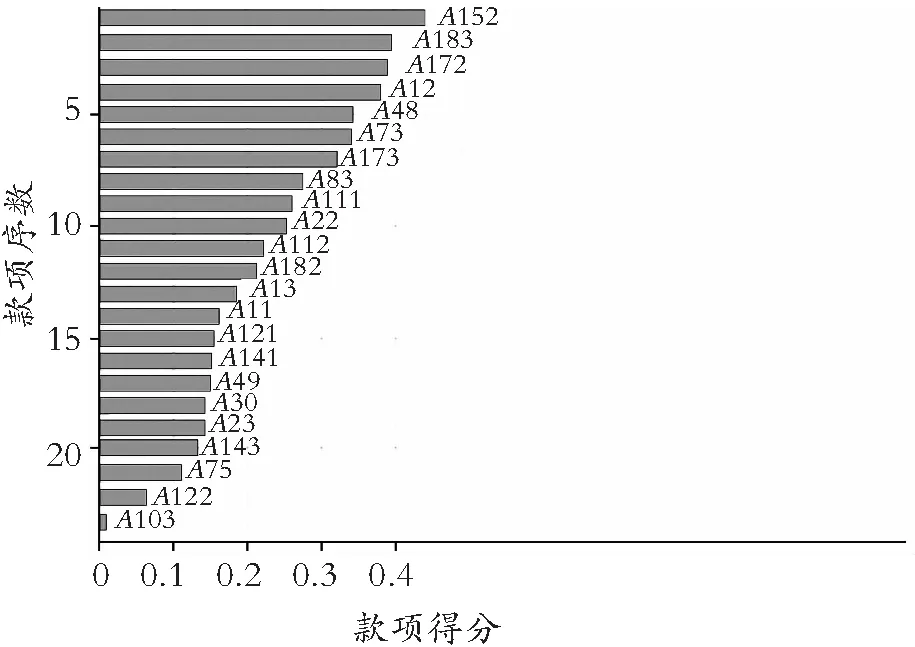
图4 重要款项得分

表2 德国个人信贷数据的重要特征

结合图4与表2，在德国信用数据集上，对信用影响最深的款项是贷款人当前住宅所有权情况。权重排名前两项的款项与借款人的个人背景信息相关，如住宅所有权、供养人数、工作年限等，而大部分的重要属性皆与个人征信信息相关，如分期付款率占可支配收入的百分比、信用历史、贷款目的等。表2依据实验结果选出与德国客户信用强相关性的重要特征，以此建立本文模型的信用评价指标以进行最终分类。此外，提取这些重要特征相关的数据进行分类实验，有效解决了信息的复杂性带来的分类困难。

2.3 异常值的处理

在重要特征提取后，考虑到原始数据中由于操作失误或者机械设备故障等原因导致的数据缺失情况。这种情况会造成数据出现不完整性、不适用性以及缺乏一致性等问题，因此需要对原始数据进行清洗，将无意义、缺失值较多的字段删除。本文在完成此步骤的基础上，为进一步优化模型的性能，通过计算个体数据间的相关性找到更具普遍代表意义的样本数据以避免个体差异较大的离群数据对实验结果的影响。使用matlab计算并绘制出显示数据间相关性程度的数量分布直方图，由图5表示。

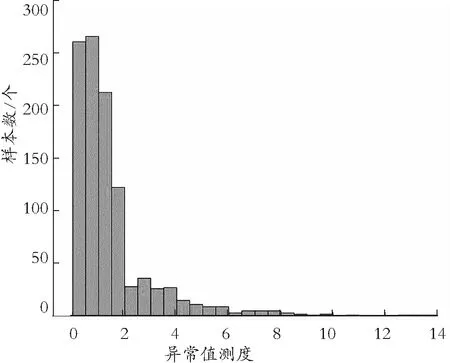
图5 数据相关性分布直方图

图5中，X轴代表数据的相关性程度，越靠近原点相关性越大；Y轴代表样本数据数量。由图5可以得知，当相关性值达到10之后，数据的个体差异性出现断层，离群性体现突出，因此在进行接下来的分类准确性实验比较之前，要去除这些离群数据，以保证模型性能的准确性。

2.4 特征提取后模型性能的比较

针对3种基于距离的相似度匹配分类性能较差的问题，利用inranked算法实现随机森林来提取重要特征，对原始信用特征进行降维和信息浓缩。本次实验中，在叶节点数为1, 决策树数为32的情况下运行inranked算法，然后在相同的实验环境下，对基于关键项和项集的样本风险性进行评估比较。实验结果如图6所示。

从图6所示的结果可以看出：3种距离测度在基于重要特征的相似性匹配性能均有明显提高。与图1相比，Chebyshev距离的识别率最高，其次是Hamming距离。当训练样本数为800时，Chebyshev距离、Hamming距离和Cosine距离的识别率分别达到88.25%,87.65%和86.75%。即使当样本量为700时，3种距离度量的谷值为76.77%，也表现出了优良的分类准确性。实验结果表明：在经过重要特征提取后的数据上，使用3个距离测度进行相似度匹配，大大提升了模型的分类性能。

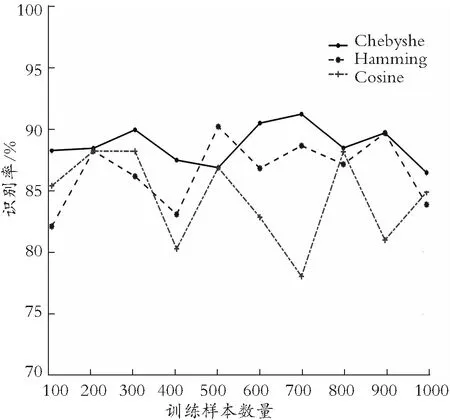
图6 3种测度在重要特征间的识别性能比较

2.5 与其他经典模型的比较

为了验证结合相似性测度与随机森林的多视角决策融合个人信用评估模型的改进效果，本文在拥有15条信用数据的德国信用数据集上随机选取1 000个训练样本，分别对8种方法进行了10次交叉验证，其平均识别率与标准差如表3所示。结果表明：本文算法平均识别率在93%以上，标准差为1.140 7，而3种基于差异的算法平均识别率均在90%以下，标准差均高于1.4，表明多视角决策融合方法具有可行性和有效性，且模型稳定性更佳。

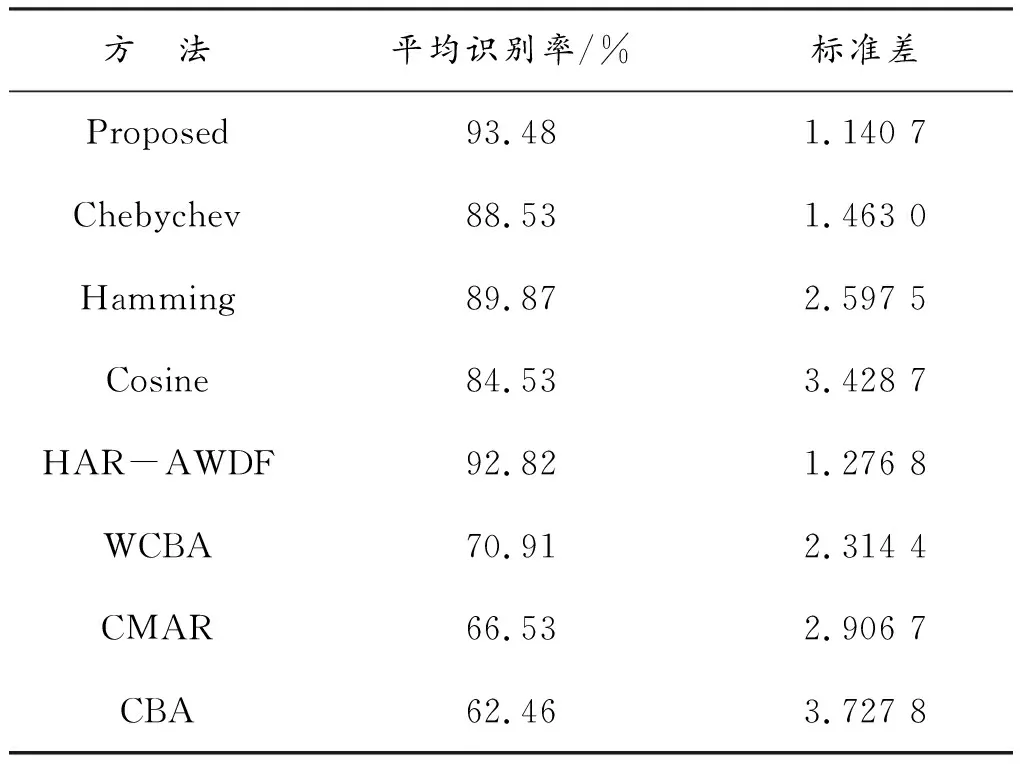
表3 与经典的方法比较

表3还表明:本文所提出的方法优于包含HAR-AWDF,CBA,WCBA和CMAR这4种具有代表性的基于重要特征提取的方法。在平均识别率方面，该算法的识别率最高为93.48%，其次是HAR-AWDF算法，识别率为92.82%，CBA算法的识别率最低，为62.46%。除了本文的模型算法和HAR-AWDF之外，基于3种不同距离度量的平均识别率都高于其他基于关联规则的分类算法。这进一步证实了准确测量客户信用调查数据之间的信用调查相似性能力对于评估个人信用调查至关重要。

3 结束语

结合随机森林方法建立的信用评价体系将3种测度与信用数据相似性匹配后得到信用风险预测的准确性。在UCI数据集中的德国信用数据集上的实验结果表明：随机森林方法自有的特征提取特性能够有效提取与分类结果有强关联性的信用特征。3种距离测度在进行特征提取与异常值去除后性能均得到了大幅提升，且识别率波动区间相对于数据预处理前显著缩小，表明了优化后的模型具有更强的稳健性。通过融合3种测度的决策可以多角度地综合信用信息，使得识别性能较单一测度显著优化， 且与其他经典组合方法比较性能更佳。将随机森林与距离测度相组合应用于个人信用评估领域为个人信用评估方法的多样性增添了新的经验。