基于EHO优化的BP神经网络污水处理出水COD预测模型

朱 琳， 李明河， 陈 园

(安徽工业大学 电气与信息工程学院， 安徽 马鞍山 243002)

0 引 言

随着近现代社会的发展，水资源缺乏、对环境保护和节能的需要、人们环保意识的加强都使得污水处理再一次成为公众讨论的热点。污水处理过程是一个干扰严重，变量繁杂多变，大时滞以及高度非线性的生化反应过程[1]。在污水处理过程中，化学需氧量(Chemical Oxygen Demand , COD)是衡量污水中有机物质含量高低的重要指标，当其数值越大，表明有机污染越严重，所以出水COD是检测出水标准的重要参数之一[2]。但是，由于COD的在线检测专用设备多采用进口元器件，价格昂贵，维护困难，而且对于化学试剂剂量添加过多可能会引起水质的二次污染且具有严重的滞后性[3]。随着产业升级推进，污水处理得到有关部门高度重视，制定了相关标准，严格要求企业排污达标，这也使得企业不得不提高标准。因此，对建立出水COD浓度预测模型的研究在水污染控制和水环境管理中具有必不可少的现实意义。

近年来，越来越多的学者开始利用建立优化后的预测模型解决污水处理中一些变量难以测量的问题。杨壮等[4]建立基于径向基神经网络与灰色理论两种模型相互结合的预测模型，并将 RBF 神经网络的预测残差用来补充灰色模型的预测结果，这样可以得到准确的 COD 预测，最后的仿真结果发现 GM-RBF 网络比常规的 RBF 网络以及 BP 网络有更高的稳定性与预测准确度。任忠铭等[5]针对污水处理中 BOD 难以测量的问题，先用搜索引力算法对数据进行特征选择，然后将选择好的特征子集作为递归 RBF 神经网络的输入来预测出水 BOD ，最后的仿真结果证明了其模型的有效性。胡赛飞等[6]提出一种出水 COD 浓度预测的模糊建模方法，将预测结果与 BSM1 模型结果进行对比，采用烟花算法优化模糊预测模型的结构与参数，实现结果发现优化后的模糊模型相对于初始模型对出水 COD 的预测更接近于 BSM1 模型，预测效果更好。陈英义等[7]建立 WT-CNN-LSTM 模型对鱼塘溶解氧进行预测，先利用小波变换将得到的样本数据进行处理，然后通过卷积神经网络与长短时记忆神经网络对数据进行拟合预测，比传统的 LSTM 以及 LSTM 的变形 GRU 的预测效果都好。顾杰等[8]利用 ARIMA 模型与改进的 BP 算法相结合，对污水水质进行全面预测，最后实验结果对比发现 ARIMA 结合 BP 神经网络的组合模型比传统的 ARIMA 预测模型精度更高，是科学、准确的河流水质指数预测方法之一。所以，建立预测模型能有效地预测污水中难以检测的参数，在一定程度上减少资源的浪费。

综上，针对污水处理中污水参数的预测建模，大多数学者更善于利用神经网络对预测过程进行相应的建模，但一般的神经网络都有着陷入局部最优解的风险，为了避免这种情况的发生，利用一般算法优化预测神经网络模型来提高模型的精确度。这种方法的优势在于可以对数据及时进行更好拟合，但上述所用的RBF 神经网络、模糊建模以及 LSTM 神经网络都较复杂，模糊建模缺乏自学习能力，并且 LSTM 网络更适用于大样本数据建模不适合小样本数据建模。BP 神经网络针对小数据样本在非线性逼近和泛化邻域更具有独特优势，利用优化算法优化改善其参数并提高寻优的能力，从而可以减少网络陷入最小值的风险，提高模型的预测能力，使其对数据进行更好地拟合，同时能对污水处理中的出水 COD 进行更加精准地预测。

BP 神经网络利用误差反向传播训练算法的特点使其具有很好的逼近非线性映射能力，该网络常被用于模式识别、系统辨识与函数拟合、对系统的最优预测和自适应控制等领域[9]，但是常规 BP 神经网络的预测模型会存在预测精度较低、收敛速度较慢等常见问题[10—12]，于是采用各种仿生群优化算法来优化 BP 神经网络参数成为了解决优化预测模型问题的方法之一。象群算法(Elephant Herding Optimization, EHO)[13]由于控制参数较少，很难陷入局部最小值，且易于实现的优点得到了人们广泛关注与研究。本文所使用的象群算法具有能很好解决参数寻优的特点，将其结合权重改进的粒子群优化算法(Particle Swarm Optimization, PSO)来优化 BP 神经网络的参数,再对污水处理中的出水 COD 进行预测能够提高预测的准确度。

1 算法优化改进

1.1 权重改进的粒子群算法

为了克服w线性递减造成的算法不能收敛到最优点的局限，选择权重改进的粒子群算法可以加快算法的收敛速度，并采用随机权重法将PSO中的惯性权重w设定为随机数。

惯性权重修改公式：

其中，N(0,1) 表示标准状态分布的随机数。

更新粒子的位移和速度：

xi,j(t+1)=xi,j(t)+vi,j(t+1)j=1,2,…,d

vi,j(t+1)=w·vi,j(t)+c1r1[pi,j-xi,j(t)]+

c2r2[pg,j-xi,j(t)]

1.2 改进的象群优化算法

EHO是由Wang等[14]在2015年提出并开发的一种群体智能优化算法，它的结构简单，参数少，易于和其他方法结合。大象是地球上哺乳动物中体型较大的动物，有自己的行为结构，体型更大，性格温顺。大象以氏群的形式生活，由一位母象首领领导，成年后，公象会离开自己的种群。大象的这种行为被表达为两种操作，分别是部族更新操作和分离操作[15-17]。

1.2.1 象群氏族更新

每一头象在氏族ci中的下一个位置都受到母象ci的影响。对于ci族中的大象j，可以更新为

Enew,ci,j=Eci,j+α(Ebest,ci-Eci,j)r

其中，Enew,ci,j、Eci,j分别是大象j在更新后的位置和上一代的位置，Ebest,ci是ci族中适应度最好的位置。α是比例因子，r为随机数。

ci族中女族长的位置Ebest,ci被定为

Ebest,ci=β×Ecenter,ci

氏族中心为

1.2.2 象群氏族分离

适应度最差的大象个体在每一代执行如下分离操作：

Eworst,ci=Emin+(Emax-Emin+1)×rand

该操作替换种群中适应度较差的个体，这种方式在某种程度上会使得算法的全局搜索能力降低，同时也不利于种群中适应度相对较差个体的去除，影响最终结果。于是，在分离机制中融合权重改进的粒子群算法来加快收敛速度，当粒子在起始阶段就接近最好点，随机得到的权值w可能会是在数据中最小的值，由此可以快速提高算法的收敛速度，同时也改善w线性递减造成的算法不能收敛到最好点的问题，增强了算法全局搜索能力。更新公式如下：

2 建立基于PSO-EHO算法优化的BP神经网络预测模型

2.1 建模过程

步骤1初始化。设置模型的各项参数，即BP神经网络结构、有学习率μ、训练误差ε以及动量因子α；随机初始化大象的位置Eci,j。

步骤2计算象群个体适应度。

步骤3执行氏族更新操作，更新个体大象的位置，若f(Enew,best,ci)>f(Ebest,ci)，更新Enew,best,ci；否则保留Eci。执行利用权值改进的SPO算法优化的氏族分离操作，若f(Enew,worst,ci)>f(Eworst,ci)更新Enew,best,ci，否则保留Eci。

步骤4针对BP神经网络中的参数权值w1、w2以及阈值b1、b2共同进行寻优，将其中适应度值的最小值确定为个体极值，得到的最优位置即为BP的权值与阈值。输入得到的数据训练样本对神经网络进行网络训练，并计算网络的实际输出和期望输出之间的误差,令其为error,即error=|y-ym|,y为实际输出，ym为期望输出。最小误差对应的大象的位置为最优个体位置，若最优个体位置满足算法结束条件，则最优位置对应神经网络的最佳权值、阈值，转步骤6。

步骤5重复步骤3和步骤4，当全局最优适应度值小于设定值的时候，转到步骤6，否则转到步骤3。

步骤6将算法寻优所获得的权值阈值设定为BP神经网络初始权值阈值，不断进行调整，直到迭代的次数达到最大的迭代次数，转到步骤7，否则转到步骤3。

步骤7根据所输入的测试样本对出水COD进行预测。

2.2 对比模型

小波神经网络是采用仿射小波变换的构造并且以小波基函数为神经非线性激活函数的神经网络[18-20]。小波网络和BP神经网络一样，通常包括3层：输入层、小波基层(即隐含层)以及输出层如图1所示。

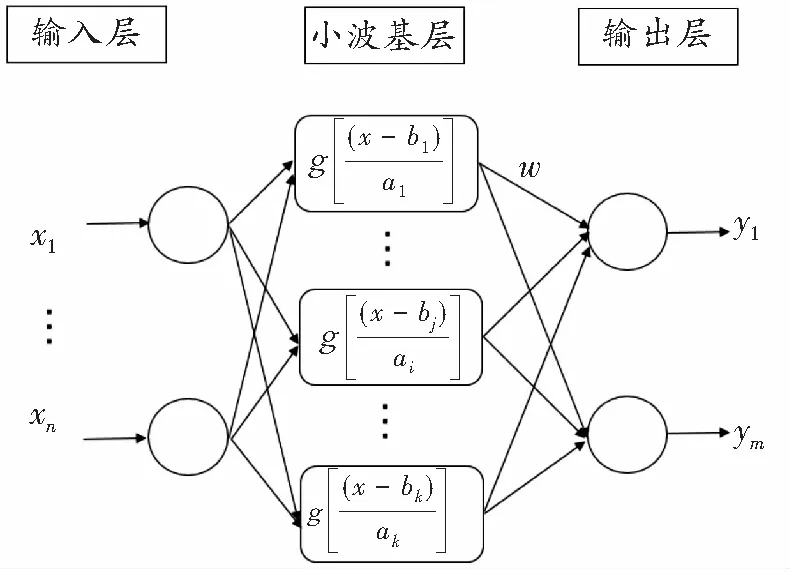
图1 小波神经网络结构

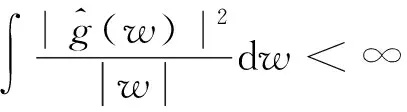
其中,a、b为实数，a不为0。

对于输入信号s(w)∈L2(R),小波变换的定义如下：

ws(a,b)≤s

小波神经网络的输入信号为

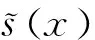
t=1,2,3,…,m

2.3 模型仿真

为了保证该模型的实际可应用性，本实验选取了某环保公司BAF 项目正常运作下各仪表现场检测的数据。为了保证建模的准确与便利，通过 SPSS 软件的数据比重分析，最终选择进水 COD 浓度、进水 NH3-N、溶解氧浓度3个变量作为输入，出水 COD 作为输出，共227组的实测数据。

将BP 网络的结构设定为3-8-1，其网络训练的最大迭代次数为300，目标训练误差为10-2，设定学习率为0.02。象群算法的参数设置：象群种群数为5，其最大迭代次数为200。

对数据的预处理包括数据样本中异常数据的剔除以及数据的归一化，首先异常数据的剔除采用的是3σ准则对超出范围的异常数据进行处理，其次为了保证消除输入输出数据间不同量纲的差异，将输入输出样本值保持在[0,1]，对训练数据进行归一化:

筛选出150组进行训练，77组进行预测，训练与预测完成后，BP 网络的输入值和输出值经过反归一化变换转换为原始数据对应实际值，其训练曲线与预测曲线的结果分别如图2、图3所示。

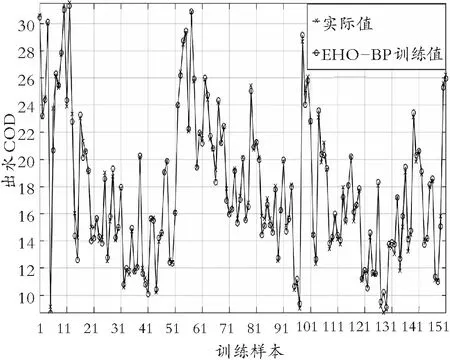
图2 EHO-BP训练曲线

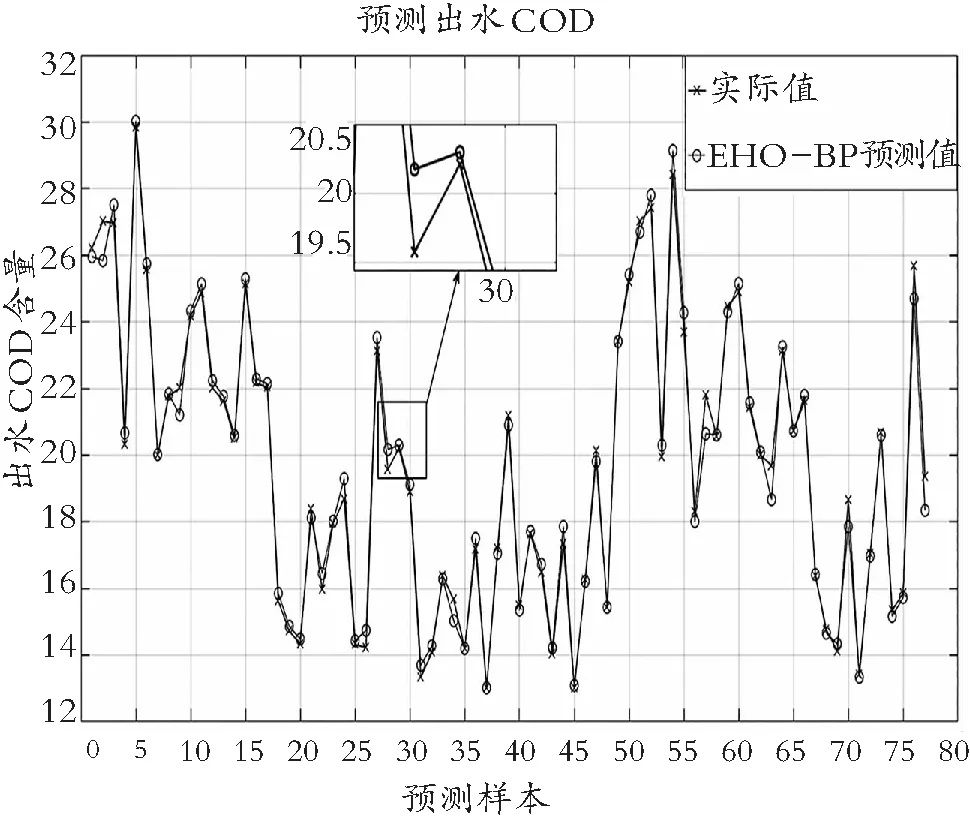
图3 EHO-BP预测曲线

因为要与建立的预测模型保持一致性，所以也将小波神经网络结构设置为3-8-1且其最大迭代次数设置成300，学习率1为0.01，学习率2为0.001，最后将小波神经网络输出的预测结果与 EHO-BP 模型预测结果进行对比，结果如图4所示。

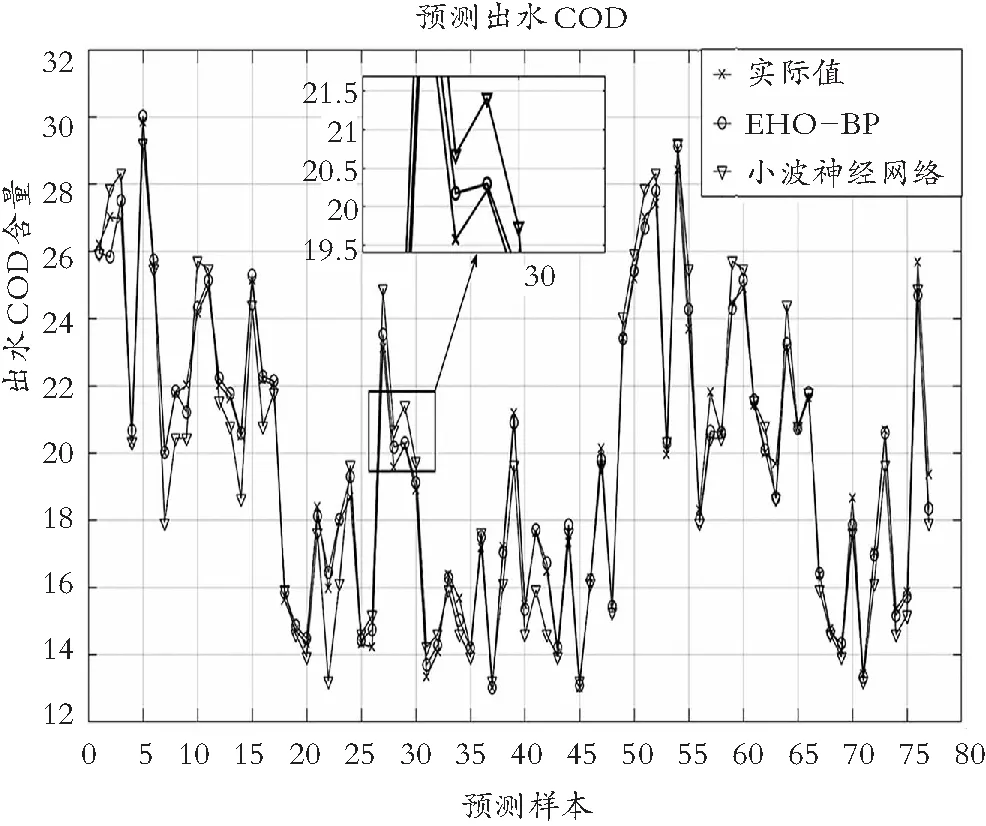
图4 EHO-BP与小波神经网络预测曲线对比图

为了进一步验证模型的预测效果，选择均方误差(MAE)和均方根误差(RMSE)来验证模型效果，公式如下：

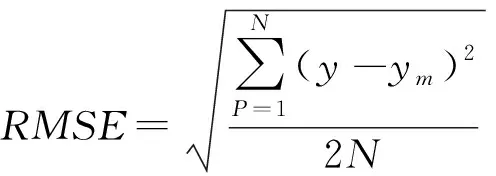
其中，N为训练样本数，y是实际的输出，ym是期望的输出，具体结果见表1。

表1 不同预测模型误差对比

由仿真实验可以看出：EHO-BP预测模型在一定程度上预测的出水COD值能达到预测标准，其预测结果相对于小波神经网络以及常规BP神经网络的准确度更高并且误差更小，所以建立的EHO-BP预测模型具有一定的可实行性。

3 结束语

本文将象群算法中的分离操作结合粒子群算法去除种群中适应度较差的个体，提高了算法寻找最优值的能力，结合BP神经网络对数据进行更好的逼近来提高预测模型预测的准确度。象群算法作为近些年来新开发的仿生算法，常被用于优化故障识别，将其与BP神经网络结合是一种新的尝试，最后的仿真结果验证了象群算法结合BP神经网络所建立的预测模型在一定程度上可以对污水处理中的出水COD进行比较准确的预测。

在后续工作中，可以将该模型放入具体的系统中进行更加完备的研究，本文只考虑了进水 COD与进水NH3-N以及溶解氧浓度这3个变量，实际的污水处理涉及的变量更多更复杂，下一步可以对流量、PH值等其他变量进行进一步研究。