非凸半无限多目标规划近似解的最优性条件

张 雯， 龙宪军, 黄应全

(重庆工商大学 数学与统计学院, 重庆 400067)

0 介 绍

半无限多目标规划问题是在约束函数个数无限的条件下研究有限多个目标函数的优化问题。它在数学、物理、工程设计、经济管理以及合作博弈等领域有着广泛的应用,目前已取得了许多研究成果[1-3]。

函数的凸性在优化理论中扮演着重要角色,特别是在建立解的充分最优性条件中起关键性作用。然而凸性条件在很多工程和经济问题中却很难满足。因此,很多学者从不同方面对凸函数进行推广,并研究了相应非凸优化问题。Golestani等[4]借助Clarke次微分在约束规格假设下得到了多目标规划问题局部(弱)有效解的必要最优性条件,并在不变凸函数的假设下,得到了多目标规划问题有效解的充分最优性条件；Chuong等[5]利用Mordukhovich次微分在极限约束规格和广义凸性条件下,分别得到了半无限多目标规划问题有效解和弱有效解的必要和充分条件。然而,在实际应用中,许多问题的精确解无法求得,利用数值算法大多只能获得其近似解。因此,研究近似解的最优性条件具有重要的理论价值和实际意义。Golestani等[6]将文献[4]中的有效解推广到近似解的情形,借助Clarke次微分在约束规格假设下得到了多目标规划问题局部ε-拟(弱)有效解的必要最优性条件,并在KT近似伪凸-仿射的条件下,得到了ε-拟(弱)有效解的必要条件；Jiao等[7]将文献[5]中的有效解推广到了近似解的情形,同样借助Mordukhovich次微分在极限约束规格和广义凸性条件下,获得了半无限单目标规划问题拟ε-有效解的必要和充分条件。值得注意的是,上述文献涉及的函数都是Lipschitz连续的。然而，在实际中许多函数并不满足局部Lipschitz这一较强的条件。如何在函数不满足局部Lipschitz假设下研究非凸半无限多目标规划问题近似解的最优性条件将是本文讨论的重点。

最近,Tung[8-9]利用切向次微分和正则条件获得了半无限多目标规划问题有效解的必要最优性条件,并在Dini-伪凸和Dini-拟凸假设下获得了(弱)有效解的充分条件；刘娟等[10]利用切向次微分研究了半无限多目标规划问题的混合型对偶。注意到,文献[8-10]中所涉及的函数不必是局部Lipschitz连续的。受文献[4-10]的启发,本文利用切向次微分研究了非凸半无限多目标规划问题近似解的最优性条件。首先引入(η,ε)-拟(弱)有效解的定义,并借助切向次微分,给出了Dini-拟不变凸函数、(η,ε)-伪不变凸函数以及严格(η,ε)-伪不变凸函数的定义。然后，利用正则条件和三类新的广义不变凸函数,获得了半无限多目标规划问题(η,ε)-拟(弱)有效解的必要和充分最优性条件。所得结果推广并改进了文献[8-9]中的主要结果。

1 预备知识

设Rn表示n维欧氏空间,用<·,·>与‖·‖分别表示Rn中的内积和范数。设S⊆Rn为非空子集,用intS，clS与coS分别表示S的内部、闭包与凸包;posS表示由S生成的凸锥；S的负极化锥和严格负极化锥分别定义为

S-:={x*∈Rn:≤0,∀x∈S}

Ss:={x*∈Rn:<0,∀x∈S}

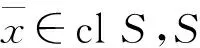
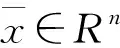
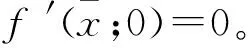
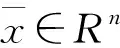
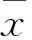
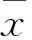
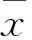
因此,有

条件C[13]设η:Rn×Rn→Rn,称函数η满足条件C,如果∀x,y∈S,∀t∈[0,1],有

η(x,x+tη(y,x))=-tη(y,x)

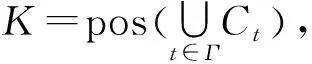
引理2[1]设S和P是两个任意的指标集(可能无限),as=a(s)=(a1(s),…,an(s))是从S到Rn的映射,ap=a(p)=(a1(p),…,an(p))是从P到Rn的映射。假设集合co{as,s∈S}+pos{ap,p∈P}是闭集,则如下表述等价:

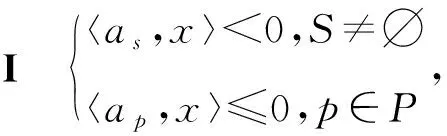
II0∈co{as,s∈S}+pos{ap,p∈P}。

2 最优性条件

考虑如下半无限多目标优化问题：

(P) minf(x)=(f1(x),…,fm(x))

s.t.gt(x)≤0,t∈T,x∈Rn

其中，fi:Rn→R,i∈I:={1,2，…,m}以及gt:Rn→R,t∈T,T是任意非空指标集(不必有限)。记问题(P)的可行集为Ω,即

Ω:={x∈Rn:gt(x)≤0,t∈T}

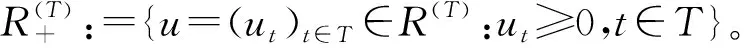
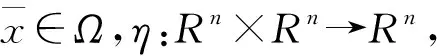
(i) 如果对任意的x∈Ω,下面不等式不成立:

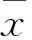
(ii) 如果对任意的x∈Ω,下面不等式不成立:

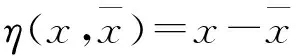
为了得到问题(P)的(η,ε)-拟弱有效解的必要最优性条件,需要如下正则条件:

首先证明如下引理:

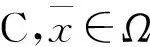
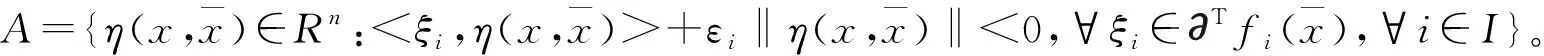
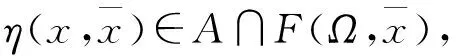
则有

(1)

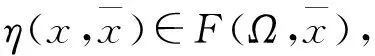
故存在N>0,对任意的k≥N,有

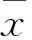
下面建立问题(P)的(η,ε)-拟弱有效解的必要最优性条件。

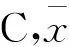
(2)

证明对任意的x∈Ω,由引理3，知

这可推得:

(3)

式(3)结合(RC1)，有

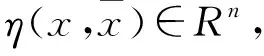
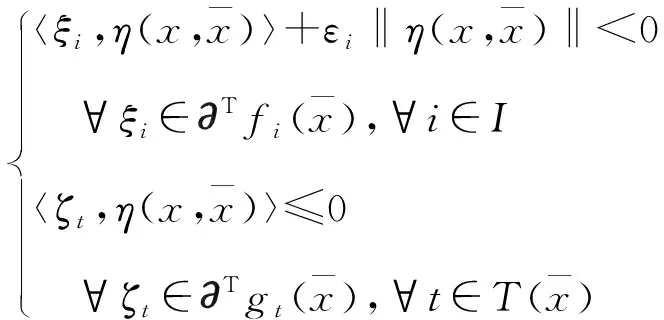
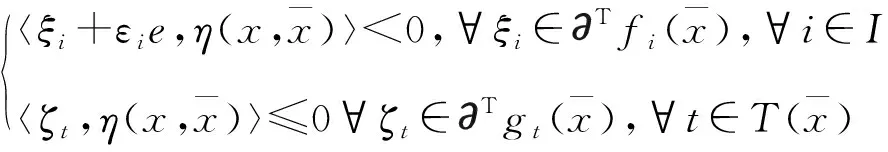
无解。由引理2，知

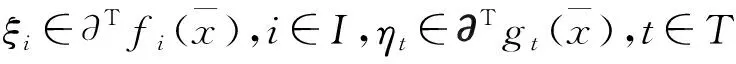
(4)

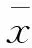
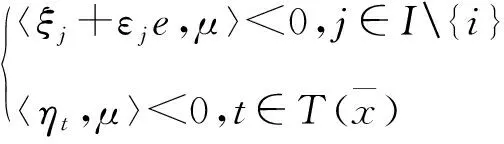
(5)

由式(5)，有

这与式(4)矛盾,因此λi>0,∀i∈I。

为了获得半无限多目标规划问题(η,ε)-拟(弱)有效解的充分最优性条件,定义如下3类广义不变凸函数。

定义3 设S⊂Rn是凸集,f:Rn→R在x∈S处是切凸的,称f在x处是

(i) Dini-拟不变凸函数,如果

f(y)≤f(x)⟹≤0
∀y∈S,∀x*∈∂Tf(x)

(ii) (η,ε)-伪不变凸函数,如果

f(y)<-ε‖η(y,x)‖
∀y∈S,∀x*∈∂Tf(x)

(iii) 严格(η,ε)-伪不变凸函数,如果

f(y)≤f(x)⟹<-ε‖η(y,x)‖
∀y∈S{x},∀x*∈∂Tf(x)

注2 当η(y,x)=y-x时,Dini-拟不变凸退化为文献[8-9]中的Dini-拟凸的定义。

下面建立问题(P)的(η,ε)-拟(弱)有效解的充分最优性条件。

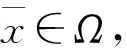
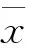
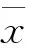
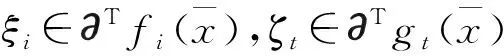
(6)

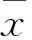
(7)

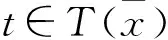
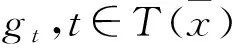
(8)

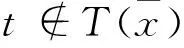
这与式(6)矛盾,故结论成立。

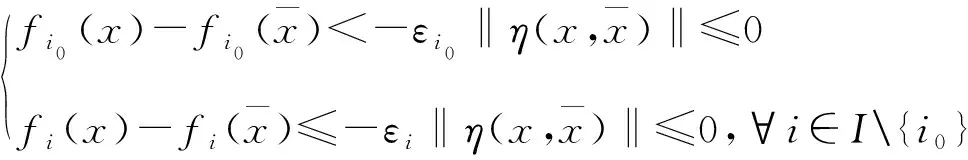
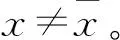
(9)

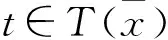
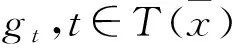
(10)

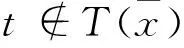
这与式(6)矛盾,故结论成立。

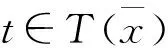
注4 定理1和定理2分别将文献[9]中的命题3.5和文献[8]中的命题3.5推广到了近似解情形。

3 结 论

利用切向次微分,研究了一类非凸半无限多目标规划问题。在正则条件下,获得了非凸半无限多目标规划问题(η,ε)-拟弱有效解的必要最优性条件。在广义不变凸性假设下,获得了非凸半无限多目标规划问题(η,ε)-拟(弱)有效解的充分最优性条件。所得结果改进了文献[8-9]中相应结果。