浅谈百分位数及其应用
2022-05-18 01:56张得志
中学生数理化·高一版 2022年5期
■张得志
新教材在统计内容中增加了“总体百分位数的估计”这一内容,这就要求同学们围绕百分位数充分了解其内涵与外延,认知其考查方向。
一、知识解读
1.第p百分位数的定义
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值。
2.计算一组n个数据的第p百分位数的步骤
第1步,按从小到大排列原始数据。第2步,计算i=n×p%。第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数。
3.四分位数
25%,50%,75%这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数,其中第25百分位数也称为第一四分位数或下四分位数,第75百分位数也称为第三四分位数或上四分位数。
二、考查方向分析
考向1:百分位数的计算
利用百分位数的概念,按照求第p百分位数的步骤求解。
例1 某车间12名工人一天生产某产品(单位:kg)的数量分别为13.8,13,13.5,15.7,13.6,14.8,14,14.6,15,15.2,15.8,15.4,则所给数据的第25,50,75 百分位数分别是____。
解:将12个数据按从小到大排序为13,13.5,13.6,13.8,14,14.6,14.8,15,15.2,15.4,15.7,15.8。


考向2:百分位数的综合应用
这类问题主要是利用频率分布直方图计算样本数据的百分位数。
例2 某年级120 名学生在一次百米测试中,成绩全部介于13s与18s之间。将测试结果分成5 组:[13,14),[14,15),[15,16),[16,17),[17,18],得到如图1所示的频率分布直方图。
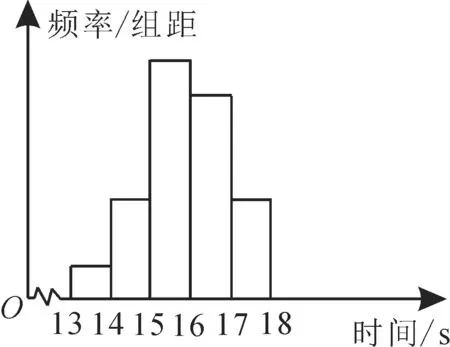
图1

猜你喜欢
湘潭大学自然科学学报(2022年2期)2022-07-28
数学年刊A辑(中文版)(2021年4期)2021-02-12
摄影之友(影像视觉)(2018年12期)2019-01-28
中等数学(2018年12期)2018-02-16
潍坊学院学报(2016年6期)2016-04-18
计算机工程(2015年8期)2015-07-03
航天返回与遥感(2014年4期)2014-07-31
河南科技(2014年11期)2014-02-27
河北工程大学学报(自然科学版)(2014年3期)2014-02-27
小朋友·快乐手工(2009年5期)2009-06-11

