统计知识核心考点综合演练
■欧阳亮 杨朝红 范俊杰
一、选择题
1.下列问题中,最适合用分层随机抽样抽取样本的是( )。
A.从10名同学中抽取3人参加座谈会
B.红星中学共有学生1600名,其中男生840名,防疫站对此校学生进行身体健康检查,抽取一个容量为200的样本
C.从2000名工人中,抽取100名调查上班途中所用时间
D.从生产流水线上,抽取样本检查产品质量
2.已知一组数据为20,30,40,50,50,60,70,80,其平均数,第60百分位数和众数的大小关系是( )。
A.平均数>第60百分位数>众数B.平均数<第60百分位数<众数
C.第60百分位数<众数<平均数
D.平均数=第60百分位数=众数
3.在发生某公共卫生事件期间,我国有关机构规定:该事件在一段时间没有发生规模群体感染的标志为“连续10天每天新增加疑似病例不超过7 人”。根据过去10 天甲,乙,丙,丁四地新增疑似病例数据,一定符合该标志的是( )。
A.甲地总体均值为3,中位数为4
B.乙地总体均值为2,总体方差大于0
C.丙地中位数为3,众数为3
D.丁地总体均值为2,总体方差为3
4.(多选题)某工厂生产A,B,C三种不同型号的产品,其相应产品数量之比为2∶5∶3,现用分层抽样方法抽出一个容量为n的样本,样本中A型号产品有16 件,则( )。
A.此样本的容量n为20
B.此样本的容量n为80
C.样本中B型号产品有40件
D.样本中B型号产品有24件
5.(多选题)某地区公共部门为了调查本地区中学生的吸烟情况,对随机抽出的编号为1~1000的1000名学生进行了调查。调查中使用了两个问题,问题1:你的编号是否为奇数? 问题2:你是否经常吸烟? 被调查者从设计好的随机装置(内有除颜色外完全相同的白球50个,红球50个)中摸出一个小球(摸完放回):摸到白球则如实回答问题1,摸到红球则如实回答问题2,回答“是”的人在一张白纸上画一个“√”,回答“否”的人什么都不用做。由于问题的答案只有“是”和“否”,而且回答的是哪个问题也是别人不知道的,因此被调查者可以毫无顾忌地给出真实的答案。最后统计得出,这1000人中,共有260 人回答“是”,则下列表述正确的是( )。
A.估计被调查者中约有510人吸烟
B.估计约有10 人对问题2 的回答为“是”
C.估计该地区约有2%的中学生吸烟
D.估计该地区约有1%的中学生吸烟
二、填空题


表1
已知在全年级中随机抽取1名学生,抽到二班女生的概率是0.2,则x=_____。现用分层抽样的方法在全年级抽取30名学生,则应在三班抽取的学生人数为____。
8.某校从参加高二年级学业水平测试的学生中抽出80 名学生,其数学成绩(均为整数)的频率分布直方图如图1所示,估计这次测试中数学成绩的平均分约为_____,众数约为_____,中位数约为_____。(结果不能整除的精确到0.1)
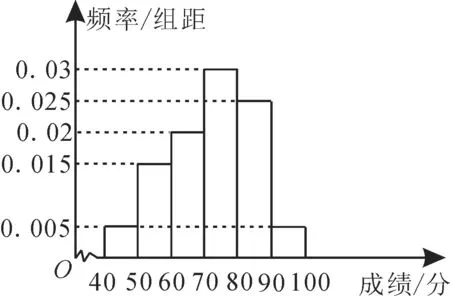
图1
三、解答题
9.某蛋糕店计划按天生产一种面包,每天生产量相同,生产成本每个6元,售价每个8元,未售出的面包降价处理,以每个5元的价格当天全部处理完。
(1)若该蛋糕店一天生产30 个这种面包,求当天的利润y(单位:元)关于当天需求量n(单位:个,n∈N)的函数解析式。
(2)蛋糕店记录了30天这种面包的日需求量(单位:个),整理得表2。

表2
假设蛋糕店在这30天内每天生产30个这种面包,求这30 天的日利润(单位:元)的平均数及方差。
(3)蛋糕店规定:若连续10 天的日需求量都不超过10个,则立即停止这种面包的生产,现给出连续10天日需求量的统计数据为“平均数为6,方差为2”,试根据该统计数据决策是否一定要停止这种面包的生产,请给出理由。
10.我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,居民生活用水定额管理,即确定一个居民月用水量(单位:t)标准x,用水量不超过x的部分按平价收费,超出x的部分按议价收费。图2是居民月均用水量的抽样频率分布直方图。
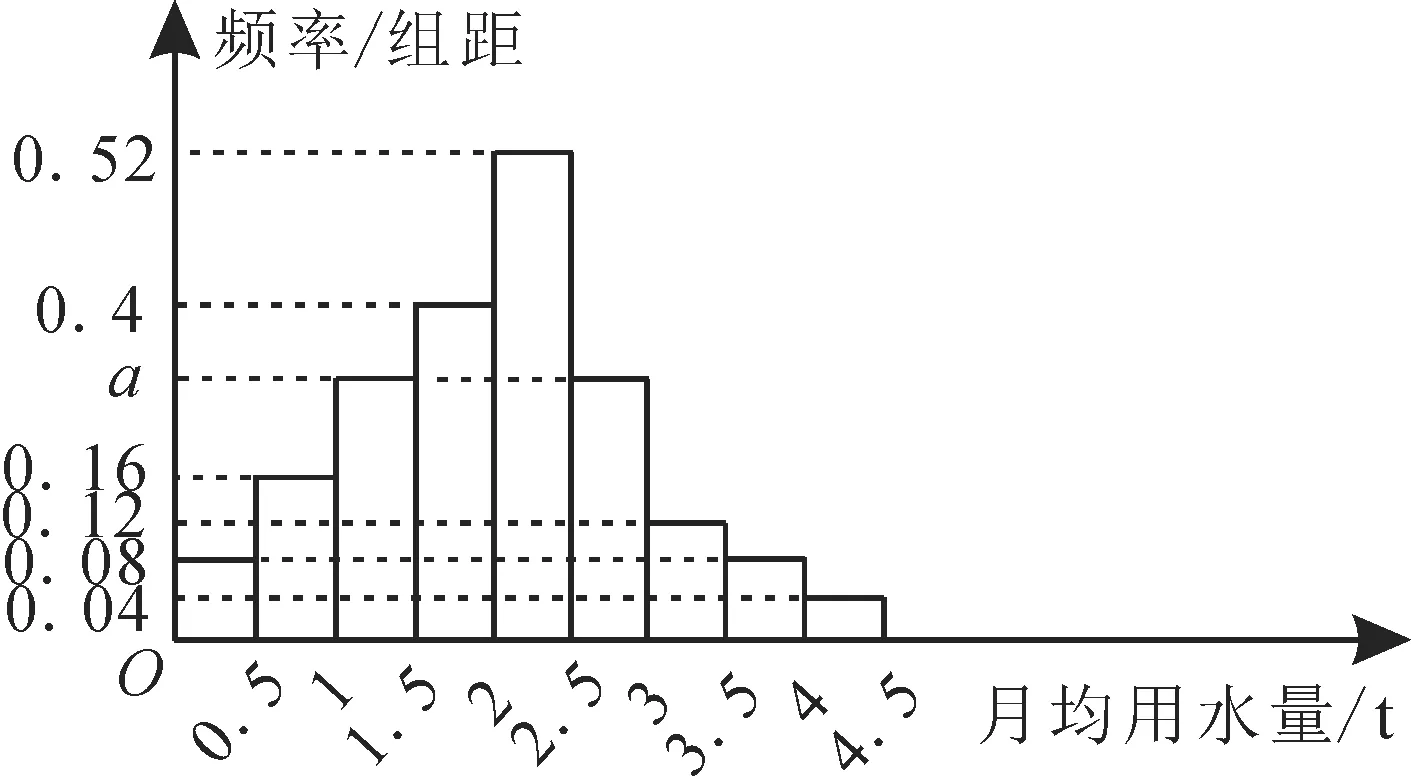
图2
(1)求频率分布直方图中a的值。
(2)试估计该市居民月均用水量的众数,平均数。
(3)设该市有30 万居民,估计全市居民中月均用水量不低于3t的人数,并说明理由。
(4)如果85%的居民希望月均用水量不超过标准x,那么标准x定为多少比较合理?
一、选择题
1.提示:B中总体个体差异明显,适合用分层随机抽样。应选B。
2.提示:易得平均数为50。因为8×60%=4.8,所以第5个数是50,即为第60百分位数。易得众数为50。应选D。


二、填空题

三、解答题



表3
由表可得这30天的日利润的平均数为59,方差为3.8。
(3)根据该统计数据,一定要停止这种面包的生产。理由如下:由方差公式得(x1-6)2+(x2-6)2+…+(x10-6)2=20,所以(xk-6)2≤20(1≤k≤10,k∈N,xk∈N),所以xk≤10,由此可以说明连续10 天的日需求量都不超过10个,即说明一定要停止这种面包的生产。
10.提示:(1)利用频率分布直方图中所有小矩形的面积之和为1,可得(0.08×2+0.16+2a+0.4+0.52+0.12+0.04)×0.5=1,解得a=0.3。

估计该市居民月均用水量的平均数为
0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.2+2.25×0.26+2.75×0.15+3.25×0.06+3.75×0.04+4.25×0.02=2.035(t)。
(3)由图知该市月均用水量不低于3t的居民的占比为(0.12+0.08+0.04)×0.5=0.12,据此估计全市居民中月均用水量不低于3t的人数为300000×0.12=36000。
(4)由图可知,月均用水量小于2.5t的居民人数所占的百分比为0.5×(0.08+0.16+0.3+0.4+0.52)=0.73,月均用水量低于3t的居民人数所占的百分比为0.73+0.5×0.3=0.88,所以x∈(2.5,3)。
由题意可得0.73+(x-2.5)×0.3=0.85,解得x=2.9。

