可转换公司债券定价中一类方程边值问题的求解

宋丽平， 姚旺进， 林建伟， 潘素娟

( 1.莆田学院 数学与金融学院， 福建 莆田 351100；2.金融数学福建省高校重点实验室， 福建 莆田 351100；3.福建商学院 信息工程学院， 福建 福州 350012 )

0 引言

研究如下形式的一个常微分方程的边值问题: 求f(x) ∈C[0，a]∩C2(0，a) ， 使得:

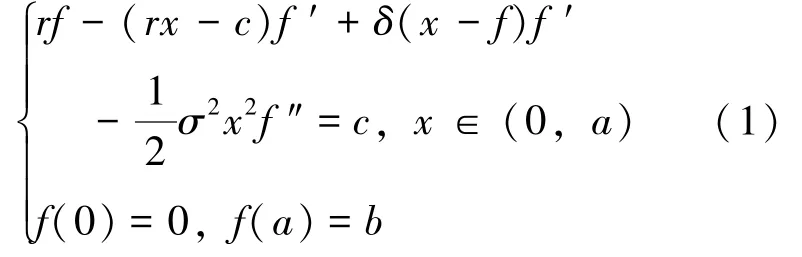
其中r，c，δ，σ，a，b均为常数， 且r ＞c≥0，r≥δ≥0，σ ＞0，a≥b ＞0。

这是一个非线性的二阶常微分方程的边值问题， 且在x ＝0 处退化， 源自Sirbu 等[1]对一类永久可转换公司债券定价问题的研究(文[1]研究的是问题(3)， 但可以证明问题(3) 等价于问题(1)， 见下文)。

特别地， 当δ＝c＝0 时，

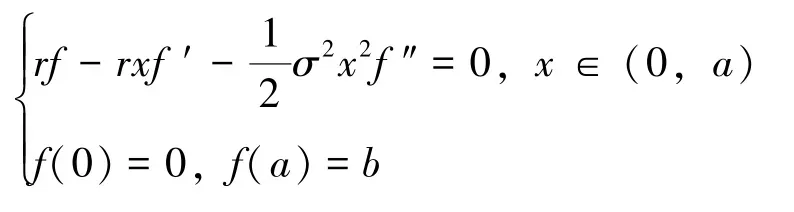
即:

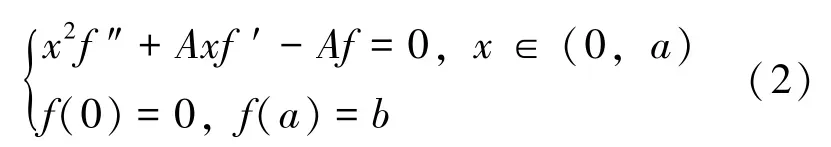
文[1]主要研究边值问题(3)(等价于问题(1))的解的存在唯一性(未求出解析解)， 本文拟研究边值问题(2)的求解方法， 并通过变量代换法与幂级数解法分别进行求解。

1 模型

可转换公司债券即可转换债券(简称可转债)， 它是一种极其复杂的信用衍生产品， 不但含有债权， 还包含着很多期权因素[2]。 在一定的条件下对公司债券进行定价是公司债券研究的重要问题之一[3]。 Brennan 等[4]、 Jonathan 等[5]通过Merton[6]的无套利定价理论和Black 等[7]的期权定价公式来研究可转债的定价问题。 然而，他们均没有考虑可转债可以提前实施， 因此没有涉及自由边界问题[8]。 此外， 也有学者应用有限元方法[9]、 蒙特卡罗模拟方法[10-11]、 三叉树方法[12]和双因子柳树方法[13-14]对可转债进行实证研究。

Sirbu 等[1]考虑可转债可以在到期日之前的任意时刻被转换或赎回。 为简单起见， 他们假设公司通过发行1 份股票和1 份可转债来融资， 且可转债为永久的， 从而可转债的价值满足一个非线性的常微分方程(如果是非永久的可转债，其价值就满足非线性的偏微分方程； 永久的情形将时间参数从问题中去掉， 则自由边界问题， 也即是关于最优转换与赎回问题， 就转化为一个自由点问题)。 下面对文[1]的模型进行简单介绍。

设某公司通过发行1 份股票和1 份可转债来融资。 可转债为永久的， 可以在任一时刻转换或赎回， 设1 份可转债可以转换为λ份股票， 即转换因子为

以X(t) 表示在t时刻转换或赎回之前的公司价值，X(t) 满足:

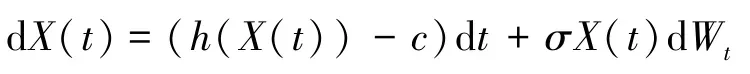
其中Wt为标准布朗(Brown) 运动，h(·) 为连续函数， 且h(0)＝0， 这里c是可转债的息票率，σ是股票的波动率，r为无风险利率，c，σ均为常数， 且r ＞c≥0，σ ＞0。

以S(t)表示t时刻的股票价值， 连续分红率为δ，r≥δ≥0； 以D(t) 表示t时刻的可转债的价值， 则X(t)＝S(t)＋D(t)。

设市场是完备和无套利的， 资产无限可分，无交易费用， 市场上存在3 种可交易资产: 股票、 可转债和无风险资产。

可转债转换和赎回方式为: 以c0和ca分别表示转换和赎回的临界值， 且c0＞0 和ca≥K(K为可转债的赎回价格) 为给定的两个数。 当X(t)≥c0时， 转换； 当X(t)≥ca时， 赎回。 一旦选定了c0＞0 和ca≥K， 关于可转债的价值D(t)有如下结论。

引理1[1]设c0＞0 和ca≥K已给定， 令a*＝c0∧ca，X(0) ∉(0，a*)，τ*＝inf{t≥0｜ X(t) ∉(0，a*)}。 则当t∈ ( 0，τ*) 时，D(t)＝f(X(t)) ， 其 中，f(x) ∈C[ 0，a*]∩C2(0，a*) 是下述边值问题的解:

其中，C[0，a*]表示[0，a*]上的连续函数的全体，C2(0，a*) 表示(0，a*) 上的二阶导数连续的函数的全体，r，c，δ，σ，γ均为常数，且r ＞c≥0，r≥δ≥0，σ ＞0，0＜γ ＜1，符号“∧” 表示“取最小值”， 符号“∨” 表示“取最大值”。

引理1 的证明见文[1]。

下面的定理1 给出边值问题(3) 与边值问题(1) 的等价性。

定理1设f(x) ∈C[0，a]∩C2(0，a)，则边值问题(3) 可表示为边值问题(1)， 即问题(3) 等价于问题(1)。

证令

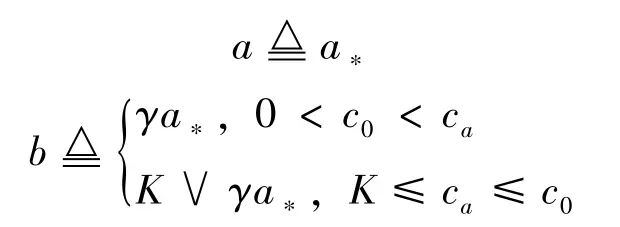
其中≜表示记为， 也就是将比较复杂的量或符号用另一个简单的符号来表示。

我们只需证明0＜b≤a。b ＞0 是显然的。下证b≤a。

当0＜c0＜ca时，

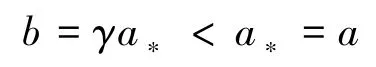
当K≤ca≤c0时，

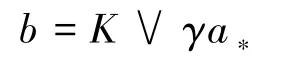
这时，

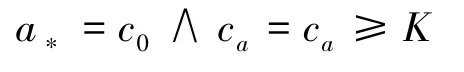
所以，

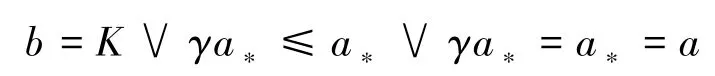
综上所述， 0＜b≤a成立。

2 变量代换法求解

本节通过变量代换将边值问题(2)转化为一个二阶常系数齐次线性方程， 进而求出边值问题(2)的解析解。 边值问题(2)的解的有关结论见定理2。

定理2设f(x) ∈C[0，a]∩C2(0，a)，则边值问题(2) 的解为:

证作变量代换x ＝et， 即t ＝lnx， 则:

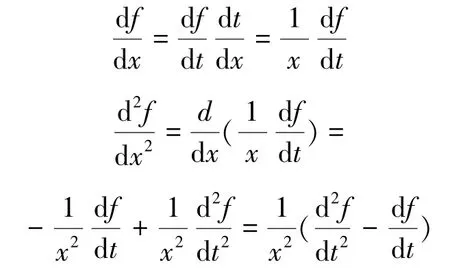
从而边值问题(2)化为:

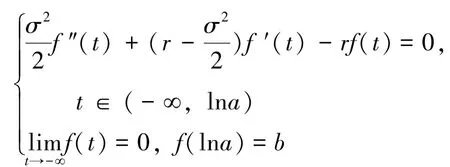
这是一个二阶常系数齐次线性方程， 其特征方程为:

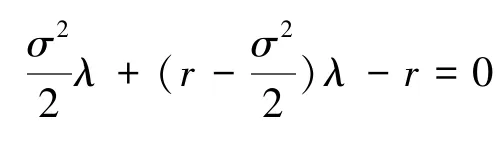
解得:

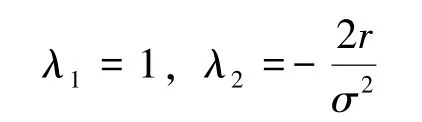
则通解为:

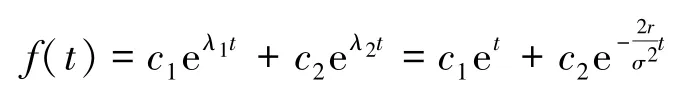
再结合定解条件， 可得:

由上面的第一个式子， 可得c2＝0； 代入上面的第二个式子， 可得

则可求得边值问题(2) 的解析解为:

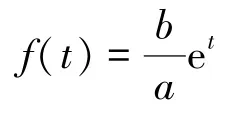
即:

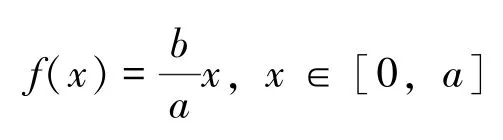
3 幂级数解法求解

本节不进行变量代换， 而是通过二阶线性微分方程的幂级数解法， 求出边值问题(2)的解析解。

首先介绍两个引理， 其中引理2 可以参见文[15]中第158～159 页的定理11， 引理3 可以参见文[15]中第153 页的内容(文[15]只对引理3的结论进行简单描述， 下面以引理的形式给出，并进行详细的证明)。

引理2[15]考虑如下形式的二阶齐次线性方程:

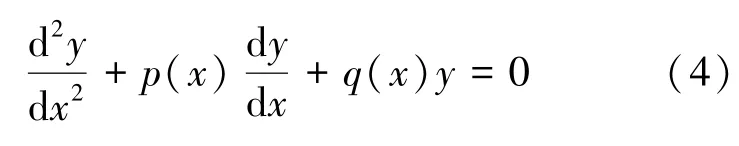
若xp(x)，x2q(x) 都能展开成x的幂级数， 且收敛区间为｜x ｜＜R， 则方程(4) 有形如

的特解， 也以｜x ｜＜R为收敛区间。 这里R为某一正常数或＋∞，a0≠0，α是一个待定的常数。

引理3[15]设y ＝y1≠0 是二阶齐次线性方程(4) 的解， 则方程(4) 的通解为:

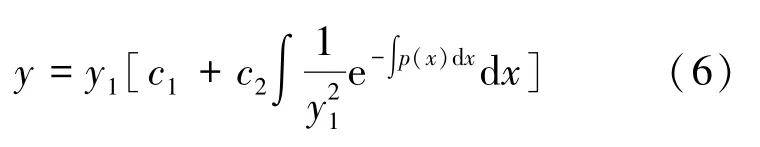
其中c1，c2为任意常数。

证令

则:

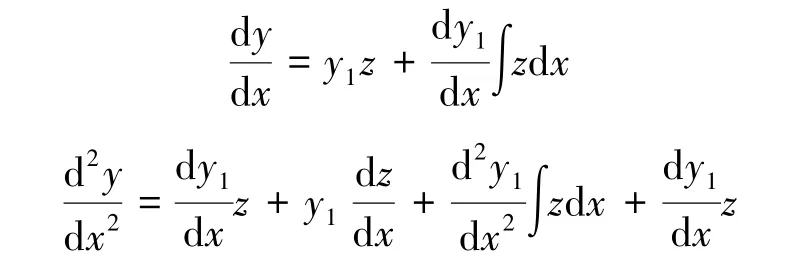
从而:

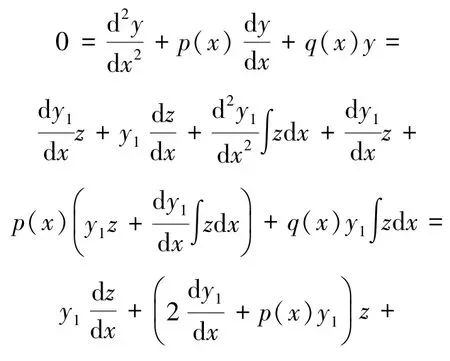
由于y ＝ y1≠0 是二阶齐次线性方程(4) 的解，故:

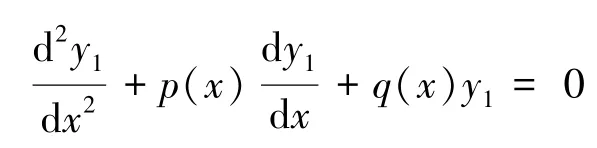
则方程(4)化为:

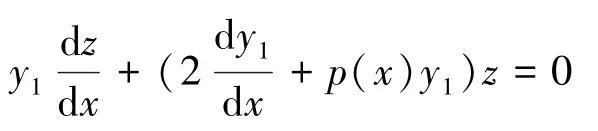
这是一个一阶常微分方程， 可变形为:

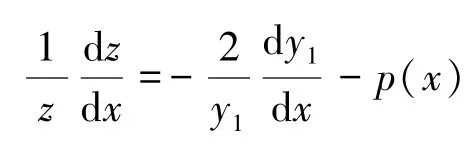
两边积分， 可求得:

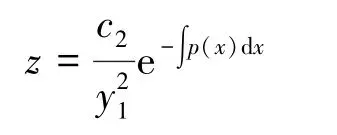
其中c2为任意常数。

从而由式(7) 可得:

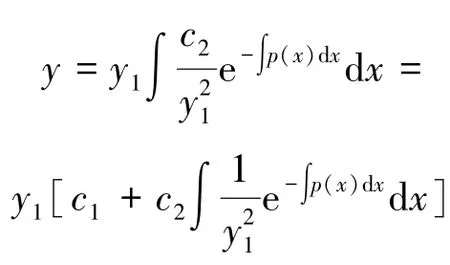
其中c1，c2为任意常数。

取c1＝0，c2＝1， 可得方程(4) 的一个特解:

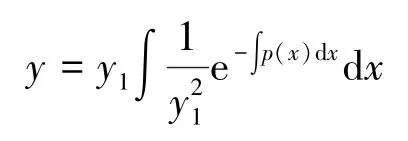
显然该特解与y1线性无关， 所以方程(4) 的通解为:

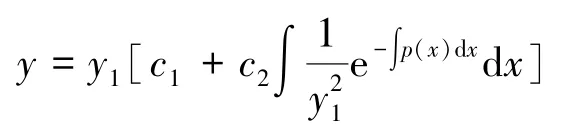
其中c1，c2为任意常数。

下面利用引理2 和引理3， 给出边值问题(2) 的幂级数解法， 即定理2 的另一种证法。

证将边值问题(2) 改写为:

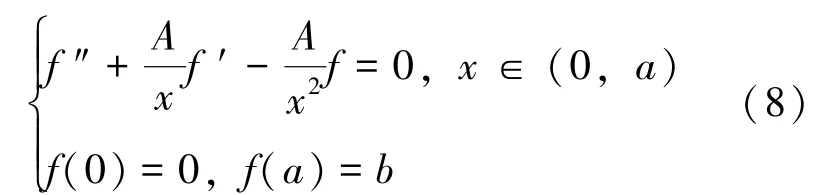
易知， 它满足引理2 的条件， 且xp(x)＝A，x2q(x)＝- A， 按x展开成的幂级数收敛区间为-∞＜x ＜＋∞， 则由引理2， 边值问题(8) 的解的形式为:

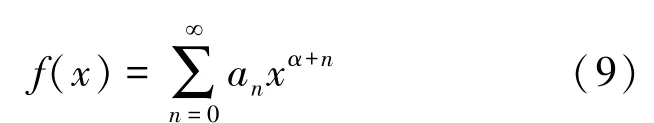
这里a0≠0， 且α，an(n ＝0， 1， 2， …) 均为待定常数。

将式(9) 代入边值问题(2) 中， 得:

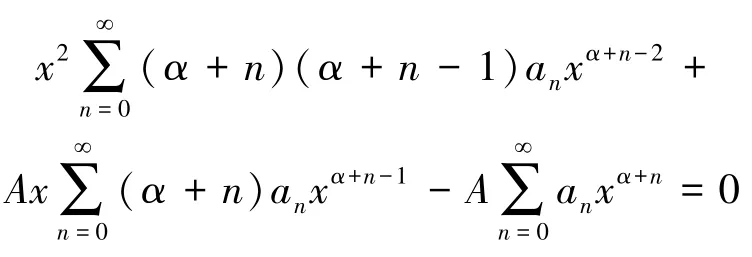
整理得:

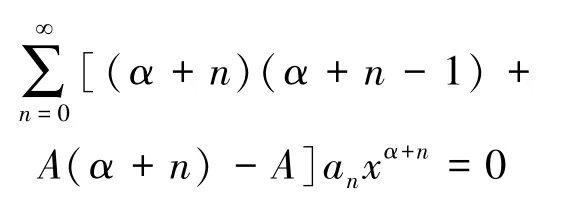
令上式中各项的系数等于零， 可得:

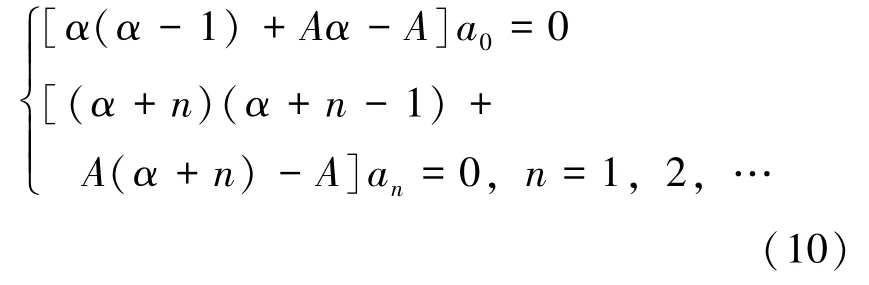
由于a0≠0， 则从(10)中的第一个方程可求得α的两个解:

第一种情况: 当α ＝α1＝1 时， 则从(10)中的其他方程， 易得:

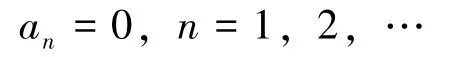
则由式(9)， 当α ＝α1＝1时， 边值问题(8)的解为

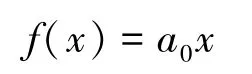
又由边值问题(8)中的定解条件

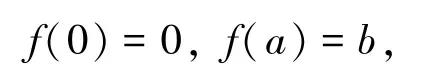
易求得:

第二种情况: 当α ＝α2＝- A时， 就不能从式(10)中来确定系数an(n ＝1， 2， …)， 因此不能像上面一样求得方程的解。 这时就只能利用引理3， 先求出边值问题(8) 的通解， 再用定解条件确定系数， 进而求出其解。

由式(6) 和上面求出的方程的特解， 可知边值问题(8) 的通解为:

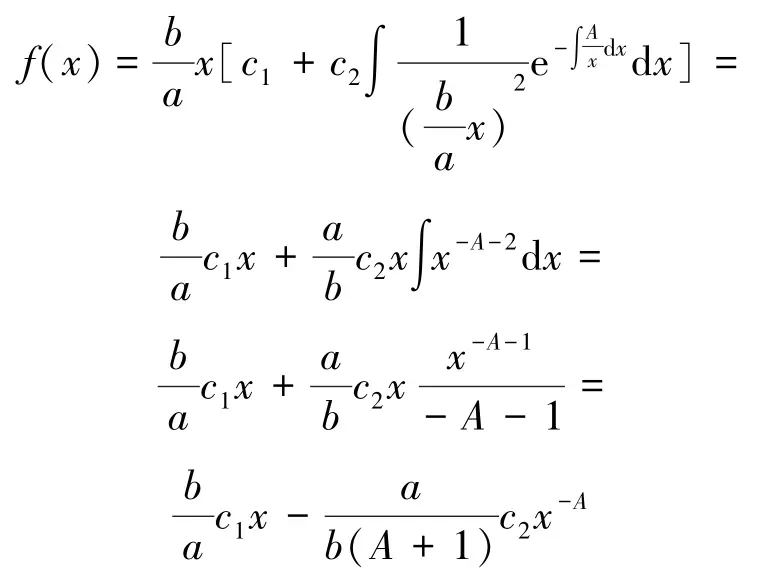
又由边值问题(8)中的定解条件f(0)＝0，f(a)＝b， 可得:

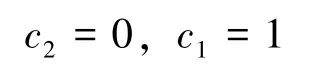
则边值问题(8)的解仍为:

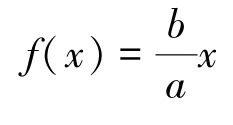
综上所述， 边值问题(8)也就是边值问题(2)的解为:

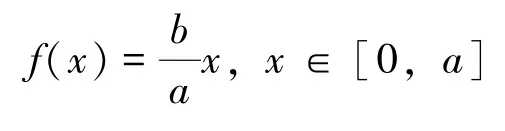
4 结论

本文主要研究如下形式的边值问题:

求f(x) ∈C[0，a]∩C2(0，a)， 使得:

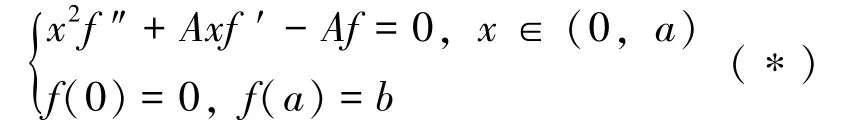
其中A，a，b均为常数， 且A ＞0， 0＜b≤a。

通过两种方法来求解边值问题(*)， 其一是利用变量代换将边值问题(*)转化为一个二阶常系数齐次线性方程， 进而求出它的解析解；其二是利用引理2 与引理3， 再通过二阶齐次线性微分方程的幂级数求解法求出边值问题(*)的解析解。

显然， 变量代换法更为简便， 但适用范围有限， 必须可以将方程转化为常系数的情形； 而幂级数求解法， 虽然更为繁琐， 但是适用范围较广， 只要是形如的二阶齐次线性微分方程， 其中xp(x)，x2q(x) 都能展开成x的幂级数， 就可以利用该方法并通过一定的计算进行求解。 此类边值问题的这两种求解方法可为可转债的合理定价提供理论基础。