二阶椭圆型方程的超定问题

阮其华

( 莆田学院 数学与金融学院， 福建 莆田 351100 )

0 引言

二阶椭圆型方程的超定问题是指二阶椭圆型方程同时满足Dirichlet 边界条件和Neumann 边界条件的这类问题。 对于一个偏微分方程， 如果区域的边界附加了太多的条件， 问题通常是不适定的， 并且方程解的存在性对区域的形状有很强的要求。 因此， 研究二阶椭圆型方程的超定问题， 就是研究在什么条件下方程的解存在。 若方程的解存在， 那么区域是什么形状。

设Ω是ℝn中光滑连通的有界区域， 考虑Ω中满足Dirichlet 和Neumann 边界条件的Poisson方程， 即:

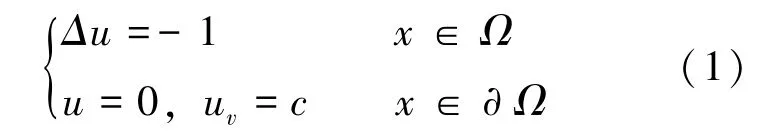
其中:v表示边界∂Ω的单位外法向向量，c是常数。

已知， 满足Dirichlet 或Neumann 边界条件的Poisson 方程的解存在， 但是同时满足Dirichlet 和Neumann 边界条件的解一般不存在， 除非区域Ω有特殊的形状。 在文[1]中， Serrin 对Poisson 方程的超定问题进行了开创性的研究， 证明了该超定问题的解存在， 当且仅当Ω是球形且u是径向函数。

近年来超定问题已成为偏微分方程研究的一个热点问题， 一些物理问题和现象可以用超定方程来描述。 在文[1-2]中， 学者给出了超定问题的物理解释， 即: Dirichlet 问题描述了一种黏性的不可压缩流体在给定截面的直管中做平行的直线运动。 如果建立直角坐标系(x，y，z)， 规定z轴为管道方向， 这时沿管道的流速u是关于x和y的函数， 并且满足Δu ＋k ＝0(其中k是与液体黏度和密度有关的常数)。 Serrin 的研究结果说明， 在附加Dirichlet 边界条件和Neumann 边界条件(即管壁上所有点在单位区域上的切向压力为常数， 表示为μuv， 其中μ是黏度) 当且仅当管的横截面是圆形， 此时水管才不易破裂。

Serrin 的研究结果极大地促进了超定问题的研究， 这里分3 个方面来介绍二阶椭圆型方程超定问题的发展。 首先， 在研究方法方面， Serrin主要利用移动平面法来证明， 随后Weinberger通过定义一个适当的辅助函数给出非常简单的证明[3]， 还有如域导数法和牛顿不等式法等其他证明方法[4-5]； 其次， 在研究区域方面， 一些学者将区域进行扩展， 如涉及缺乏边界正则性的区域[6]、 外域[7]和环形域[8]等； 再次， 在研究方程方面， 一些学者将方程进行扩展， 如比Poisson 方程更一般的退化椭圆型方程[9]、 抛物线型方程[10]和带权Laplacian 方程[11]等， 关于带权Laplacian 方程的相关研究可见文[12]。 然而也有一些学者研究非常数边界条件的超定问题， 如Neumann 边界条件非常数的超定问题[13]、 涉及边界曲率的超定问题[14]和常曲率空间中的超定问题[15]。 Bianchini 等在文[4]的基础上， 研究各向异性p-拉普拉斯方程的Serrin 型问题[16]。 有关超定问题的文献非常多， 在此不一一列出。

本文主要介绍二阶椭圆型方程超定问题的一些最新研究动态， 分3 个部分来介绍二阶椭圆型方程超定问题的发展， 分别为: 平面上一类超定问题[17]、 一类加权Poisson 方程的超定问题[11]和p-扭转刚性问题的形状优化[18]。

1 关于平面上一类超定问题

本节介绍解的Laplacian 算子不等于-1， 而是等于一般的函数- f(u)， 并且在边界上同时满足Dirichlet 和Nuemann 边界条件的超定问题， 即:

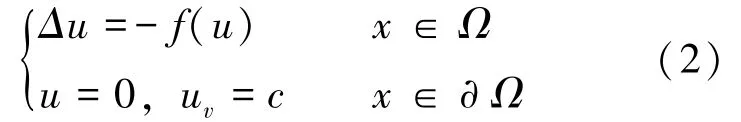
在文[19]中， Lakhdar 研究了平面上一类超定问题， 并给出了解存在的必要条件， 但这个条件要求比较高。 这里考虑降低文[19]中的条件， 得到相应超定问题解存在的必要条件。

定理1[17]设Ω是平面上光滑连通的有界区域，是超定问题(2) 的经典解， 如果f ＞0，f′≤0 并且表示Ω的面积，那么Ω是一个圆。

定理1 推广了文[19]中的结论， 利用定理1 可以得到如下推论:

推论1[17]设Ω是平面上光滑连通的有界区域，是超定问题(2) 的经典解， 如果f ＞0，f′≤0 并且uf(u) ≥c2＋1，那么Ω是一个圆。

定理2[17]设Ω是平面上光滑连通的有界区域，是超定问题(2) 的经典解， 如果f(u) ≤f(0) 并且边界的平均曲率H表示边界的弧长， 那么Ω是一个圆。

2 一类加权Poisson 方程的超定问题

本节介绍如下加权Poisson 方程的超定问题:

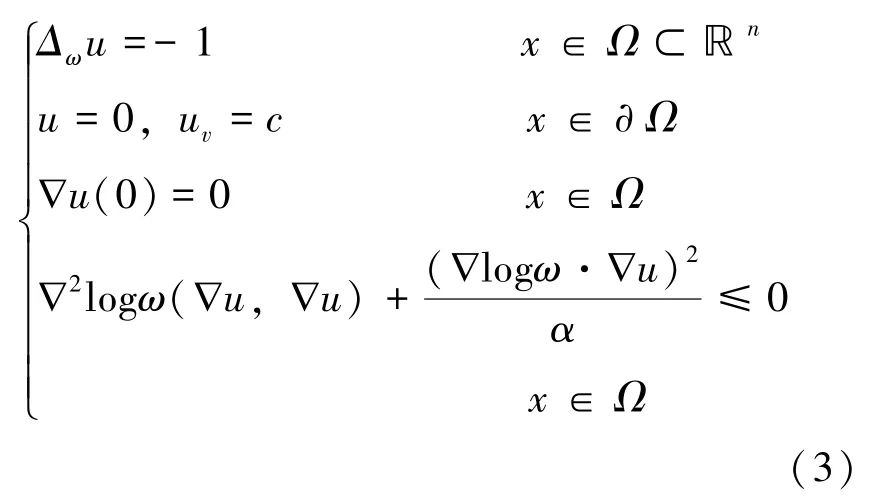
其中加权Laplacian 算子定义为Δω ＝Δ ＋∇logω·∇，ω∈C2，γ(ℝn＼ 0) 表示阶数为α ＞0 的齐次正函数， 即: ∇ω·x ＝αω(例如，ω ＝｜x ｜α)。

以下介绍加权Poisson 方程超定问题的若干研究结果。

定理3[11]设Ω是ℝn中边界光滑的连通有界区域， 若超定问题(3) 有解u∈C2(Ω)， 则区域Ω是以原点o为球心的球。

当u是径向对称解时， ∇ω·x ＝αω蕴含因此，得到如下推论:

推论2[11]设Ω是ℝn中边界光滑的连通有界区域， 若超定问题(3) 有径向解u∈C2(Ω)，则区域Ω是以原点o为球心的球。

下面给出超定问题(3) 的一个存在性结果:

定理4[11]设Ω是ℝn中以R为半径、o为球心的球， 则是超定问题(3)的解。

作为定理4 的应用， 可得到Ω中加权调和函数的一个平均值性质。 若Ω中函数h∈C2(Ω)满足Δωh ＝0， 则称其为加权调和函数。 如果加权函数ω为常数， 那么加权调和函数即为调和函数。 加权调和函数具有与调和函数相似的性质，例如， 欧式空间中的每一个有界调和函数都是一个常数[21]。

定理5[11]设在Ω ＝B(0，R)中加权函数ω满足∇ω·x ＝αω， 则对任意加权调和函数h∈C2(Ω)， 下面的平均值性质成立， 即:

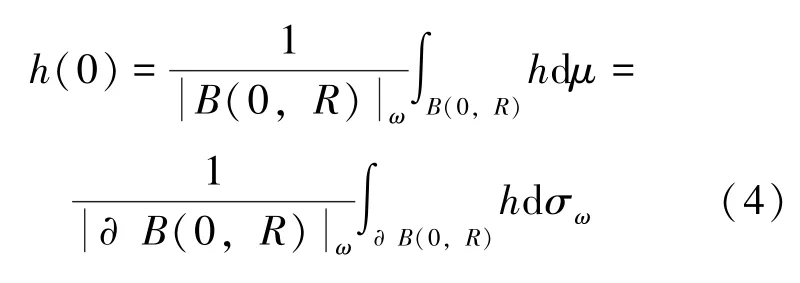
最后讨论Neumann 边界条件非常数的超定问题。 设Ω⊆ℝn为内部严格包含原点的有界区域， 对任意表示欧式空间中x与原点的距离函数。 在文[22]中， Tewodros 证明若如下超定问题有解u∈C2(Ω)，

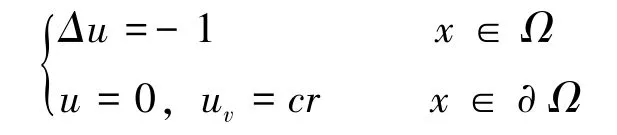
其中c是常数， 则区域Ω是一个球形。 上述证明主要是基于极大值原理和Pohožaev 恒等式[23]。这里不使用极大值原理， 而是使用了一些初等不等式和分部积分公式来证明上述结果同样适用于加权Poisson 方程的超定问题。

定理6[11]设Ω是ℝn中边界光滑的连通有界区域， 考虑如下超定问题:

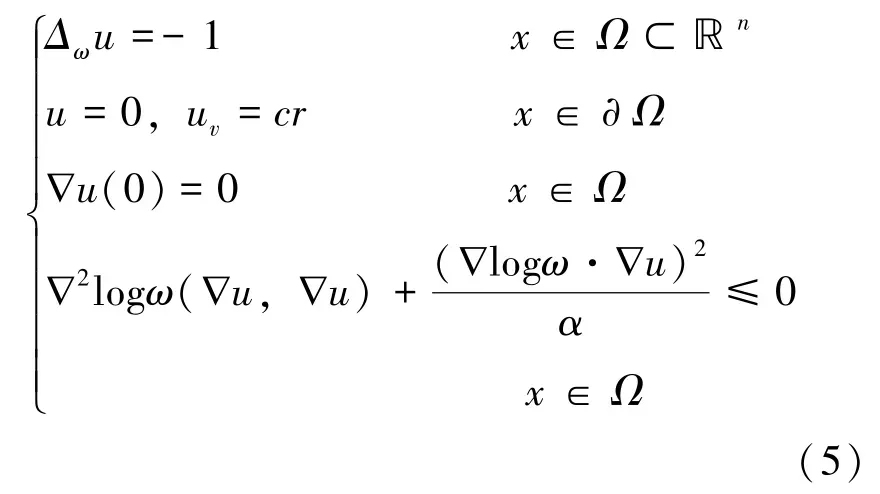
其中c是常数， 如果问题(5) 有解u∈C2(Ω)，那么区域Ω是一个球形。

3 关于p-扭转刚性问题的形状优化

设Ω是ℝn中具有光滑边界的连通有界区域， 考虑如下的p-扭转刚性问题:

定义1设φ∈(Ω)是任意具有紧支集的光滑函数， 称u∈，p(Ω) 是问题(6) 的弱解当且仅当

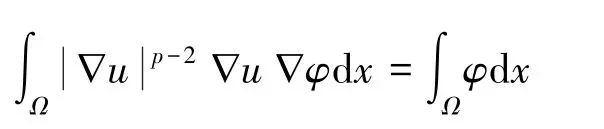
已知p-扭转刚性问题(6) 有唯一解u∈C1，α， 这里α∈(0， 1)， 具体可见文[24]。 一般地， 在∇u ＝0 处u不是C2(Ω) 的。

定义2设A是ℝn中具有光滑边界的所有连通有界区域集合， 若

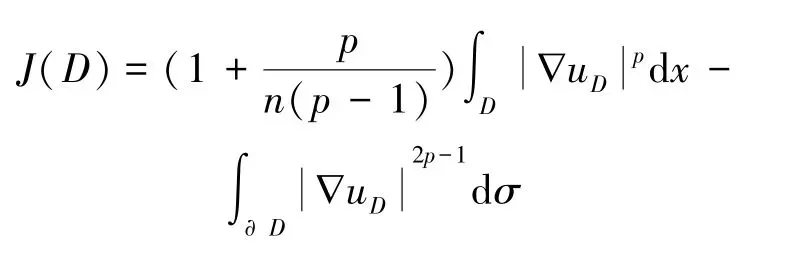
则称J(D) 是关于区域D的泛函， 简称域泛函。这里对每个D∈A，uD∈W1，p(D)∩C1(¯D)是p-扭转刚性问题(6) 的解。

考虑最优化问题:

2014 年Farjudian 等研究了定义在光滑有界的体积约束区域Aε ＝{D⊆ℝn:D为满足体积上p-扭转刚性问题的另一个域泛函， 定义为:他们推广了Talenti 在文[26]中的经典结果。

当p ＝2 时， Choulli 等在文[5]中利用域导数和Alexandrov 在文[27]中的定理给出了超定问题(8) 的另一个证明:

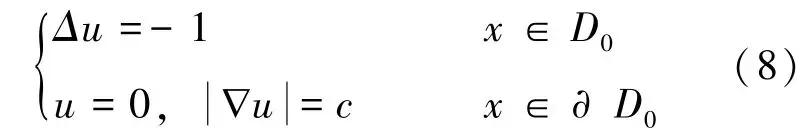
即D0是域泛函J(D)的最优形状当且仅当超定问题(8)有解， 那么由Serrin 的研究结果知，D0是球形。 事实上， 这个结果可以由文[5]直接推出， 因为在p ＝2 时， 文[5]的证明对任意D∈A，J(D)≥0 成立。 若存在区域D0使得J(D0)＝0 使得其中I表示单位矩阵， 因此， 所以根据Drichlet 边界条件知D0是球形。

研究p-扭转刚性问题(6)的最优区域， 不是简单地从p ＝2 推广到更一般的情况， 因为当p≠2 时， 不能从J(D0) 推出等式∇2u ＝-所以不能使用p ＝2 时获得的最优区域的办法。 为了克服这个困难， 需引进辅助函数， 利用Bernstein 的方法证明该函数在边界上是常数，那么由Dirichlet 边界条件可知在边界上是常数。

在文[9]中， Garofalo 等证明了如下p-扭转刚性超定问题:

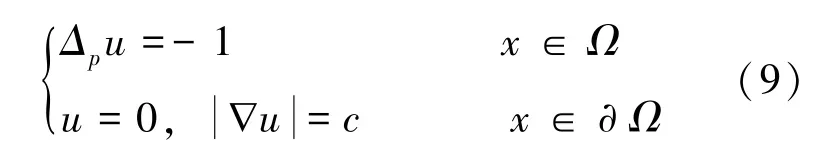
下面介绍得到关于p-扭转刚性问题的一些结果。

定理7[18]设D0是ℝn中具有光滑边界的连通有界区域， 假设u(x) ∈W1，p(D0) ∩C1(¯D0)是在Ω ＝D0中p-扭转刚性问题(6)的解， 那么D0是域泛函J(D)在A中的最优形状当且仅当u(x)是超定问题(9) 在Ω ＝D0中的解。

根据Garofalo 等在文[9]中的结果， 得到如下推论:

推论3[18]域泛函J(D)在A中的最优形状是球形。

超定问题(9) 最早由Garofalo 等在文[9]中利用Weinberger 的方法证明。 目前为止超定问题(9) 还没有其他的证明方法。 这里利用文[5]中域导数的方法， 给出了超定问题(9) 的另一个证明， 并得到如下结果:

定理8[18]设Ω ＝D0是ℝn中具有光滑边界的连通有界区域， 如果超定问题(9) 有解u∈W1，p(D0) ∩C1(¯D0)， 那么D0是球形。