具有破产重组条款公司最优红利分配问题

林建伟， 林 琦

(1.莆田学院 数学与金融学院， 福建 莆田 351100；2.金融数学福建省高校重点实验室， 福建 莆田 351100)

0 引言

红利分配是公司财务管理的一个核心问题。公司所采取的红利分配策略会直接影响公司未来的经营状况和融资能力， 同时也会深刻影响投资者的投资决策。 红利分配问题最早由De Finetti提出， 他认为选择最优红利策略的标准是: 公司通过这一红利分配策略将使得自己从初始时刻至破产时刻(公司资产盈余降为零)期间公司所获得的红利贴现值总和最大； 并在公司资产盈余演化过程服从离散布朗运动条件下， 证明了公司的最优红利分配策略为障碍策略[1]。 De Finetti 的工作具有开创性意义， 之后许多学者在该工作的基础上做进一步的推广。 Jeanblanc-Picque 等在公司资产盈余演化过程服从布朗运动条件下考虑了公司最优红利分配问题[2]； Avram 等在公司资产盈余演化过程服从Levy 过程下研究了公司最优红利分配问题， 同时考虑了固定交易费对于最优红利分配策略的影响[3-4]； Akyildirim 等在随机利率背景下考虑了公司最优红利分配问题[5]；Reppen 等在公司资产盈余演化过程服从带有随机收益率布朗运动模型下研究了公司最优红利分配问题[6]。 在实证研究方面， 刘琼芳分析了民生财政与社会分红理论的内在契合性[7]； 张英婕等探讨了国有企业红利分配与资本收益收取的关系[8]。 但上述研究都假定公司仅在公司资产盈余降为零时破产， 且不考虑公司破产重组的可能。 实际上， 公司碰到财务危机时， 往往在公司资产盈余降为零之前申请破产保护， 对公司的资产进行重组， 以期重整。 鉴于此， 文章将在文[2]的基础上， 基于自我协商破产重组模式， 推广考虑具有正的破产边界下公司最优红利分配问题。

1 最优红利分配问题的数学模型

1.1 基本假定

Ⅰ市场无风险利率为常数r。

Ⅱ公司为股份制公司， 假定公司投资人由一个大股东和一个小股东构成， 公司运行期间大小股东按股权比例获得红利收益。

Ⅲ在概率测度空间(Ω，Ft{ }t≥0，F，Q)上， 公司的资产盈余演化过程Xt服从:

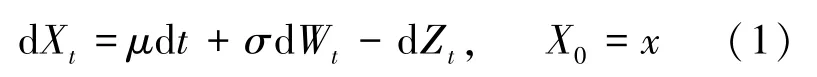
式(1)中，x≥0 表示公司的初始资产盈余，μ，σ分别表示公司资产盈余的收益率和波动率，Wt表示标准的布朗运动，Zt表示红利的累积过程。

ⅣZt演化过程服从:

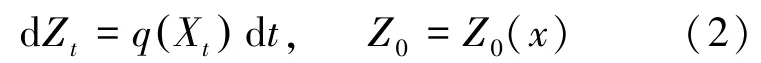
式(2)中，q ＝q(x)，Z0＝Z0(x) 是任意一个可测函数， 分别表示为单位时间内红利支付率和初始红利支付额， 两者满足限制条件为0≤q(x)≤K ＜∞， 0 ≤Z0(x) ≤x，K为最大的红利支付率。

Ⅴ最优红利分配策略选择标准: 大股东有权选择红利分配策略， 其选择的最优红利分配策略旨在保证公司从初始时刻至破产时刻期间公司所获得的红利贴现值总和和剩余公司资产盈余贴现值两部分之和最大。

Ⅵ自我协商破产重组模式: 当公司财务面临困难时， 大股东有权在公司资产盈余降为零之前， 即降到B(0 ≤B≤x) 时提前申请破产保护，同时大小股东自我协商对公司资产进行重组， 以期摆脱困境， 提高公司投资者的青睐程度， 并将公司向投资者出售获得B元。

1.2 数学模型

基于上述基本假定， 对于任意给定的B(0 ≤B≤x) ， 公司的破产时间τ定义为:

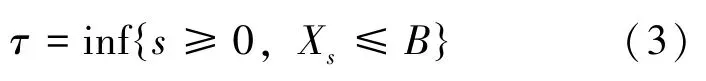
且规定t≥τ， dXt ＝dZt ＝0。

基于基本假定Ⅴ关于最优红利分配策略选择标准的界定和破产时间定义(3)， 公司最优红利分配问题的数学模型表示为:

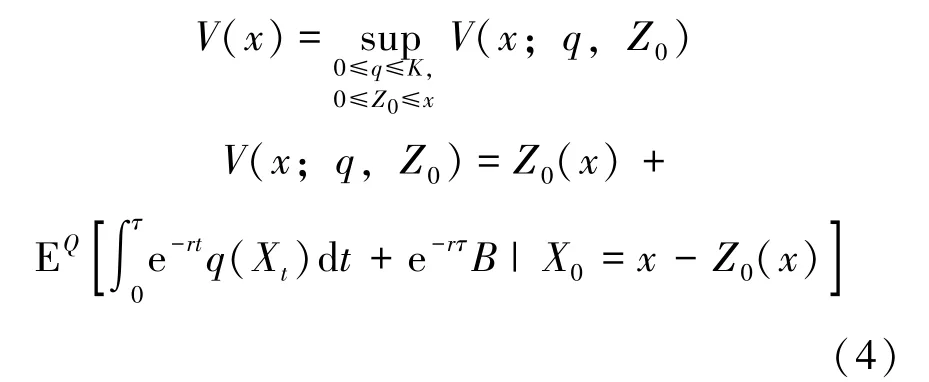
式(4)中，V(x) 表示在最优红利分配策略下的值函数，q，Z0为随机控制变量，V(x；q，Z0) 表示在给定一种红利分配策略下的值函数。

为了进一步简化问题， 数学模型(4)可等价转化为:

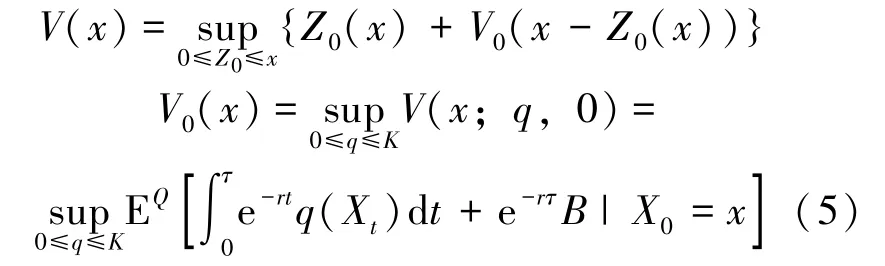
注意到V0(x) 为解决问题的关键， 其特征为Z0≡0。

2 值函数的求解和最优红利分配策略

2.1 值函数V0(x) 满足的H 问题

基于数学模型(5)， 运用动态规划原理， 可推出值函数V0(x) 满足的H 问题(HJB 方程和定解条件)。 通常记为满足H 问题的解， 然后通过验证定理证明就是值函数V0(x) 。满足的H 问题为:

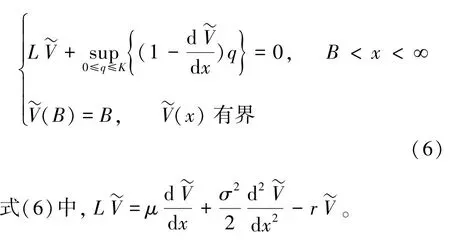
式(7)中，在x ＝b上满足的3 个连接条件分别解释为在b点连续、 光滑通过和二阶导数连续。

运用微分方程的方法和分析的技巧， 对¯H问题(7)进行求解， 得到如下结果。

定理1对于任意给定参数r，μ，σ， 当B时， 存在唯一b*(B ＜b*＜∞) ， 使得解的解析表达式为:

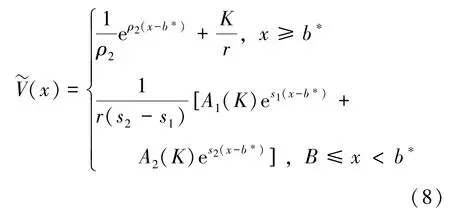
其中，

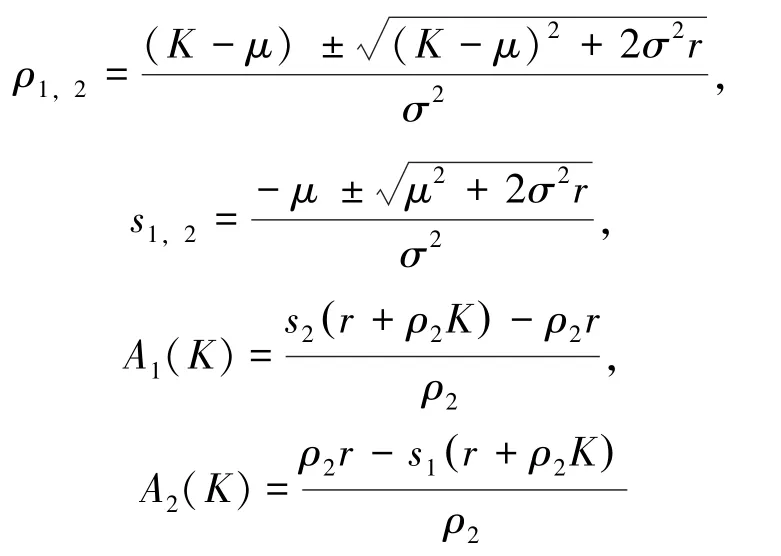
K*为关于K方程A1(K)＋A2(K)＋Br(s1- s2)＝0 唯一的正根，

b*为关于b方程唯一大于B的根。

证基于H 问题(7)， 当x ＞b时， 由V~(x)所满足的方程， 可知能表示为:由于有界， 当x→∞时， 可推出C1＝0。

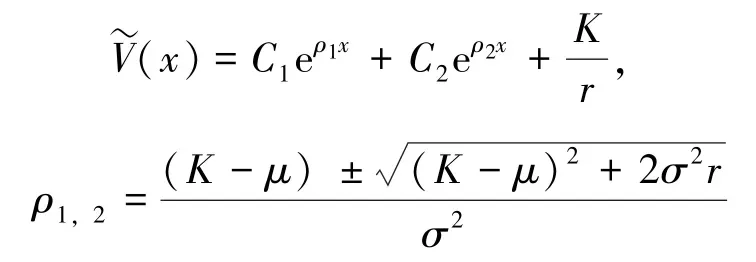
当B ＜x ＜b时， 由所满足的方程，可知V~(x) 能表示为:

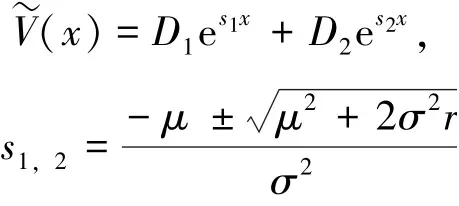
这 里

再由边界条件， 可得A1(K)es1(B-b)＋A2(K)es2(B-b)＋Br(s1- s2)＝0。

接下来的关键问题是要考虑什么条件下上述关于b的方程存在唯一大于B的根。

首先， 分析A1(K)，A2(K) 的性质， 可验证:

即μs2- r ＜A1(K) ≤0， 0＜r - μs1＜A2(K) ≤

其 次， 记f(b；K，B)＝ A1(K)es1(B-b)＋A2(K)es2(B-b)＋Br(s1-s2) ， 根 据A1(K) ≤0，A2(K)＞0，s1＞0，s2＜0， 可验证＞0。 为了使得方程f(b；K，B)＝0 在(B， ∞)上存在唯一的根， 其充要条件为f(B；K，B)＜0， 即A1(K)＋A2(K)＋Br(s1- s2)＜0。

最 后， 记(K)＝ A1(K)＋ A2(K)＋Br(s1- s2) ， 根据A1(K)，A2(K) 的性质， 可验证

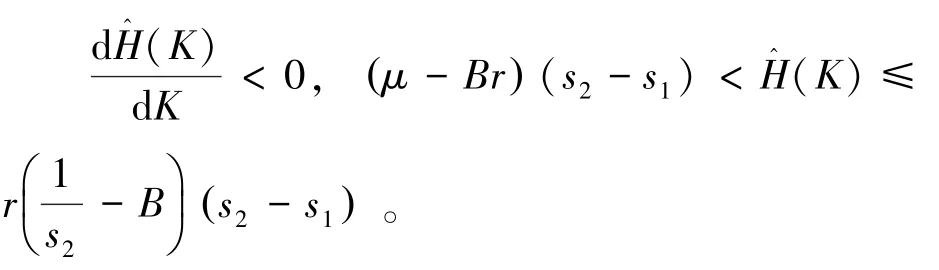
由公式(8)， 当x≥b*时，当B≤x ＜b*时，

现在将证明0(x) ， 且给出最优红利分配策略。 把结果形成如下定理。

定理2对于任意给定参数r，μ，σ， 当就是所要求的V0(x) ， 且获得最优红利分配策略为:Z0(x)＝0，x≥0 和这里，K*，b*的定义见定理1。

证对于应用Itô 公式， 可得:

由的表达式(8)， 可验证｜V~′(x)｜有界， 根据鞅的性质， 可知

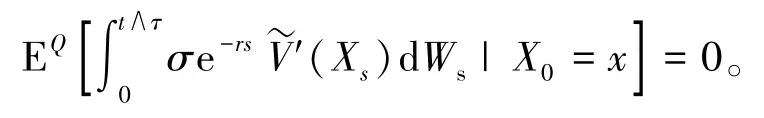
让

因此，≥V(x；q， 0) 。 由于q(x) 的任意性， 可证≥V0(x) 。

另 外， 取q(x)＝ q*(x) ， 对 于应用Itô 公式， 可得:

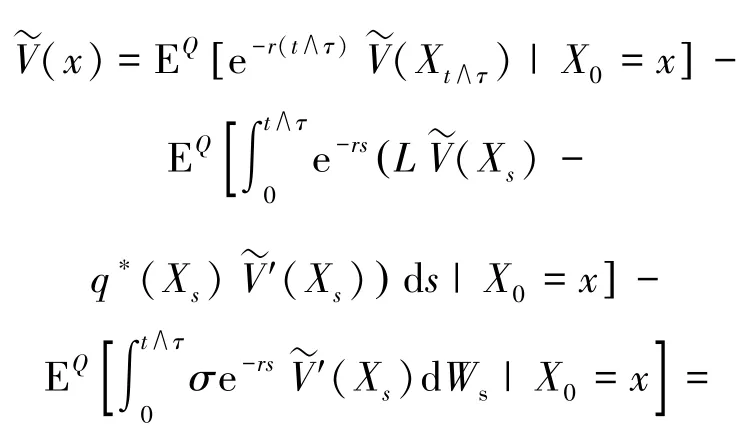
因此，(x；q*， 0)， 即≤V0(x) 。综上， 证明了0(x) ， 且获得的最优红利分配策略为q*(x) 。 定理2 证明完毕。

2.2 值函数V(x)和最优红利分配策略

根据式(5) 和0(x) ， 可得:

记f1(y)(x - y)， 0 ≤y≤x，f1′(y)＝1(x - y) 。

当B≤x ＜b*时，(x) ≥1，f1′(y) ≤0，因此， 此时选择Z0(x)＝0 时， 达到最大值， 即V(x)。

当x≥b*时，≤1，f1′(y) ≥0， 0 ≤y≤x -b*， 因此， 此时选择Z0(x)＝x -b*时，达到最大值； 同理f1′(y) ≤0，x -b*≤y≤x，因此， 此时也选择Z0(x)＝x - b*时， 达到最大值； 总之， 选择Z0(x)＝x -b*时， 达到最大值，V(x)＝x - b*(b*) 。

把上面分析结果形成定理如下。

定理3对于任意给定参数r，μ，σ， 当B ＜时， 存在唯一b*(B ＜b*＜∞) ， 使得最优红利分配策略为:

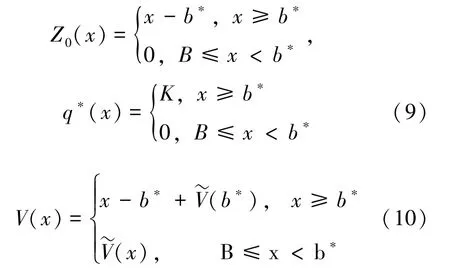
这里，K*，b*的定义和解的表达式见定理1。

注: 当B ＝0 时， 定理3 的结论退化为文[2]的结果。

3 结论

本文考虑到股东在公司资产盈余下降到零之前有权提前申请破产保护和进行自我协商破产重组特征， 在公司资产盈余演化过程服从布朗运动模型下， 利用随机控制的理论和方法， 建立了具有正的破产边界下公司最优红利分配策略的数学模型。 运用动态规划原理， 获得了数学模型中值函数所满足的H 问题(HJB 方程和定解条件)，并利用微分方程方法和分析的技巧， 获得了H问题解存在时破产边界和红利支付率上限所满足的限制条件， 进而求解出H 问题解的解析表达式。 最后， 采用Itô 公式和鞅的性质， 证明了H问题的解就是值函数的解， 并给出了最优红利分配策略。