一种再入飞行器结构的热流载荷反演方法

刘子昂，陈 强，吴邵庆，李彦斌，费庆国

(1. 东南大学机械工程学院，南京 211189；2. 东南大学江苏省空天机械装备工程研究中心，南京 211189)

0 引 言

再入飞行器在进出大气层时，其结构与外侧空气相互摩擦，表面将产生大量热能，形成强烈的气动加热效应。结构表面的热流会沿飞行器结构向内传递，进而影响飞行器结构静、动力学特性，严重时可导致结构发生强度破坏。因此，准确掌握再入飞行器结构在实际服役过程中所面临的热流载荷，对飞行器结构设计和评估至关重要。然而，直接测量服役状态下再入飞行器结构表面的热流载荷存在诸多难点：一方面，再入飞行器服役于严酷的力/热/振动/噪声等复杂环境，将热流传感器布置于飞行器外侧容易遭受多场载荷环境影响；另一方面，在再入飞行器表面的热防护结构中集成传感器的难度较大。预埋测温晶粒为一种对热防护结构影响小的测量方式，但此方法只能记录服役过程中的最高温度，难以准确反映温度随时间变化的特征。近年来所发展的载荷反演方法通过在再入飞行器内部布置温度传感器并测量其内壁面温度，进而求解传热学反问题(Inverse heat conduction problem, IHCP)得到外壁面热载荷，成为获取再入飞行器热流载荷的有效手段。

传热学反问题作为一类典型的不适定性问题，对定解数据的扰动极为敏感，国内外学者已通过各类数值方法开展了相关研究。钱炜祺等采用顺序函数法对简单平板结构表面瞬变热流进行反演，以当前时刻后若干时刻的结果对当前时刻热流进行反演，反演结果依赖于用于反演的时刻数量。Lu等基于共轭梯度法，利用弯管外侧布置的温度传感器获得的数据对薄壁弯管结构内部流体温度进行反演；在弯管内外温差不大的情况下共轭梯度法有着较好的反演结果。相比于顺序函数法，共轭梯度法中没有人为设定的参数，并且反演精度和计算速度与顺序函数法相当，因此共轭梯度法有着更好的适用性。黄少君等采用随机优化算法对热源位置进行反演。随机优化算法相比于梯度方法在跳出局部最优解上有着一定的优势，但由于其计算量大、计算时间长，难以用于复杂结构上的热流载荷反演。Lu等基于Tikhonov正则化方法以及共轭梯度法对三维瞬态热传导分析问题进行反演，通过正则化方法降低测量误差对反演结果的影响。对于较厚的结构，Khajehpour等采用域分解法，将结构沿厚度方向划分为若干个区域，分区域对热流进行识别，识别结果相比于对整个结构直接识别有更高的精度。现有研究大多针对简单的厚板、圆管等结构，采用一维传热模型进行热载荷反演，仅能考虑结构沿厚度方向的热量传递。而对于实际结构，热载荷不仅会沿厚度方向传递，同样会由于外表面温度的非均匀性使得热量沿面内方向传递。再入飞行器尺寸较大，并且外形复杂。采用再入飞行器结构简化传热模型时，其在实际工况下的计算结果将存在较大误差。

此外，现有研究大多采用较为简单的热载荷进行理论研究和仿真分析，取得了较好的识别效果，但这些方法在复杂热载荷工况下的稳定性和收敛性有待研究。Nakamura等基于顺序函数法以及奇异值分解法对飞行器再入阶段表面热流进行反演；通过在计算中引入奇异值分解法降低了测量噪声对反演结果的影响，使得反演结果不会由于过度拟合从而偏离真实值。邵元培等针对飞行器中的烧蚀情况，考虑结构表面几何域的变化反演其表面热流。

对于再入飞行器而言，其服役过程中结构处于上千摄氏度的高温中。此时材料的热导率、比热容相比于常温下有着很大的差异，材料热物性参数随温度的变化会引起传热的非线性特性。薛齐文等基于T形板结构,在考虑材料温变热物性参数的基础上，用共轭梯度法对热物性参数以及边界条件同时进行反演，基于数值仿真分析的手段探讨了测点数目、测量误差和变量初值对反演结果的影响。Bergagi等基于共轭梯度法求解边界上的温度，考虑了材料的温变热物性参数对反演结果的影响，证明了此方法可以较好地反演薄壁结构的温度边界载荷。Xiong等结合共轭梯度法以及顺序函数法的优点，提出了顺序共轭梯度法,当测量数据受较大噪声影响时，此方法具有高于传统顺序函数法的计算精度以及高于传统共轭梯度法的计算速度。

本文针对再入飞行器的热流载荷反演问题开展研究。首先，介绍基于共轭梯度法的热流载荷反演理论基础。进而，针对一维结构开展热流载荷反演的数值分析，讨论材料温变热物性参数、温度传感器测量误差等因素对反演结果的影响。然后，针对典型热防护结构和返回舱结构,结合有限元方法开展热流载荷反演的数值分析，并讨论测点位置对反演结果的影响。

1 热流载荷反演的理论基础

再入飞行器在服役过程中面临复杂的热流载荷，为了更好地拟合热流载荷变化，将整个时程均匀离散为若干个时程节点，其中各个节点之间的热流载荷由两个相邻节点的热流载荷差值获得。

假定结构所受热流时程曲线函数为()，分布规律的空间函数为()，则全域上热流载荷为：

(,)=()()

(1)

式中:为结构热流载荷所处边界上的位置矢量。

将传热过程均匀划分为个时间节点。在结构上选取个位置作为模拟布置传感器的位置，所受热流载荷边界上选取个位置。以此个位置的温度时程曲线为已知值，以个位置的热流时程曲线为反演值，建立优化目标函数：

(2)

式中：mea,,为第个传感器测量点时刻的测量温度，cal,,为第个传感器测量点时刻的反演结果计算值。当小于极小值之后，认为其收敛，得到反演结果。

,为第个点的热流时程曲线时刻的热流值，则目标函数对未知参量,求偏导数，可得到目标函数的梯度为：

=1,2,…,;=1,2,…,

(3)

热流时程曲线参量的迭代式为：

(,)+1=(,)-(,),

=1,2,…,;=1,2,…,

(4)

式中:表示迭代步数，(,)表示第次迭代计算中获得第个点的热流时程曲线时刻的热流值，表示迭代步长，,表示对第个热流时程曲线时刻热流值的迭代搜索方向。,由下式获得：

=1,2,…,;=1,2,…,

(5)

(6)

式中:为共轭系数；当=0时，=0。

计算中的迭代步长为：

=

(7)

2 热流载荷反演验证算例研究

为验证热流反演方法的准确性，并探讨影响反演结果的因素。针对如图1所示的一维传热模型，采用有限体积法(Finite volume method, FVM)进行瞬态传热正问题分析计算。以结构右侧的仿真温度结果，反演其左侧的热流载荷。

2.1 有限体积法瞬态传热计算

对于一维情况下采用有限体积法将总长度为的区域离散为长度为Δ的个控制体，如图1所示，其中=0处为热流入射面，=处为绝热面，以此处的仿真结果模拟温度传感器的测量值。

图1 有限体积法中的控制体离散Fig.1 Discretization of the control volume in finite volume method

依据能量守恒定律，对于每个控制体有：

(-)Δ=Δ

(8)

式中:为单个控制体的输入热流，为单个控制体的输出热流，为控制体面积，为材料密度，为材料比热容，Δ为时间间隔。

对于控制体,,…,-1其输入输出热流为：

(9)

式中:为材料热导率，为第个控制体的温度。

联立式(8)和式(9)，可得：

(10)

定义式(11)所示的傅里叶数，式(10)可简化为：

(11)

()(+1+-1-2)=1

(12)

依据实际工况设定第1个控制体与第个控制体为第二类边界条件。控制体1边界为外界热流输入面，控制体为绝热边界，则边界条件为：

(13)

式中:为环境输入热流。

2.2 热流载荷反演算例

对于如图1所示的一维结构在=0处施加如式(14)所示热流载荷：

()=-+300,0≤≤300

(14)

基于有限体积法计算热传导正问题获取控制体的仿真值。以此仿真值模拟结构内部的实际测量温度值。通过共轭梯度法对外侧热流载荷进行反演，计算流程图如图2所示。分别考虑材料热物性参数为常数和温变参数时的热流反演结果，如图3所示。

反演热流载荷的平均误差为：

(15)

式中：为真实热流值，为反演热流值。

图2 共轭梯度法反演热流载荷流程图Fig.2 Flow chart of heat flux identification using conjugate gradient method

由图3可知，材料热物性为常数时，反演热流平均误差为6.84 mW·mm；材料热物性为温变参数时，反演热流平均误差为3.88 mW·mm。当考虑材料热物性参数为常数时，其反演误差明显高于考虑材料热物性为温变参数的结果。同时，这一误差会随着结构整体温度的升高而增大。这是因为材料在高温时的热导率和比热容与常温时相比有着很大差异。因此很有必要在热流载荷反演中考虑材料热物性随温度的变化特征。

图3 热流载荷的反演结果Fig.3 Identification results of heat flux

为模拟温度传感器的测量误差，在仿真温度值的基础上施加方差为0.5、均值为0的随机误差。依据3σ准则，其误差所在区间为[-2.12 K, 2.12 K]。由于反演结果对测量误差的敏感性较高，且容易产生过拟合的情况。因此，需要对加噪声之后的数据进行降噪处理。采用降噪处理后的数据与未降噪处理的模拟温度测量数据对热流载荷进行反演，反演得到的热流载荷如图4所示。

图4 测量数据含噪声时热流反演结果Fig.4 Identified results of heat flux with noisy measurement data

表1中列出了在模拟测量结果上考虑不同测量误差情况下热流反演结果的误差。由表1和图4可知，当考虑温度传感器测量误差时，其反演结果会受到较大的影响，特别是这种误差会导致反演的结果在真值附近出现较大的震荡。为了减小这种由于测量误差所造成的反演误差，一方面需要采用降噪方法，降低测量误差对反演结果的影响；另一方面需要制定合适的收敛准则，使其不会因为迭代次数过多产生对测量数据的过度拟合。

表1 测量数据含噪声时热流反演误差Table 1 Error in identified heat flux with noisy measurement data

以测量噪声方差为0.5，均值为0的反演结果为例，分析反演过程中目标函数与热流误差的收敛过程，如图5所示。其中热流反演平均误差以式(15)计算。

图5 反演结果随迭代次数的变化Fig.5 Variation of the identified results with respect to the number of iterations

当考虑温度传感器测量误差时，随着迭代次数的增加,目标函数值不断减小，但热流反演结果的误差却不会一直减小。这说明目标函数值越小并不等同于反演结果越好。由于测量误差的存在，会导致共轭梯度法计算过程中各个时刻的搜寻方向出现误差，从而影响最终的反演结果。因此，在制定共轭梯度法的收敛准则时，不仅要设置目标函数达到的最小值，也需要考虑下降速率。当目标函数下降速率较低时需要停止计算，防止过拟合。

3 实际结构算例研究

为验证热流反演方法在再入飞行器上的运用，并探讨影响反演结果的因素。本节首先针对夹芯式热防护结构，反演二维结构表面均匀分布的热流载荷；进而，针对典型再入飞行器返回舱，反演三维结构上所受热流载荷。

3.1 热流载荷

再入飞行器在服役过程中所受热流载荷取决于飞行器的形状、上升轨迹和再入条件等因素。参考文献[21]中采用了如图6中真实值曲线所示的一种两级入轨飞行器在概念设计中采用的热流载荷。为使热流反演更贴近实际情况，在实际结构热流反演计算中采用此热流载荷作为结构的热流载荷。

图6 含测量误差时热流反演结果Fig.6 Identified results of heat flux with measurement error

3.2 夹芯式热防护结构热流载荷反演

本文所研究的夹芯式热防护结构，其从外至内分别包括复合材料面板结构、气凝胶结构、复合材料面板结构、胶层以及内侧金属底板。各层的厚度依次为2 mm、28 mm、0.5 mm、2 mm、5 mm，结构有限元模型如图7所示。

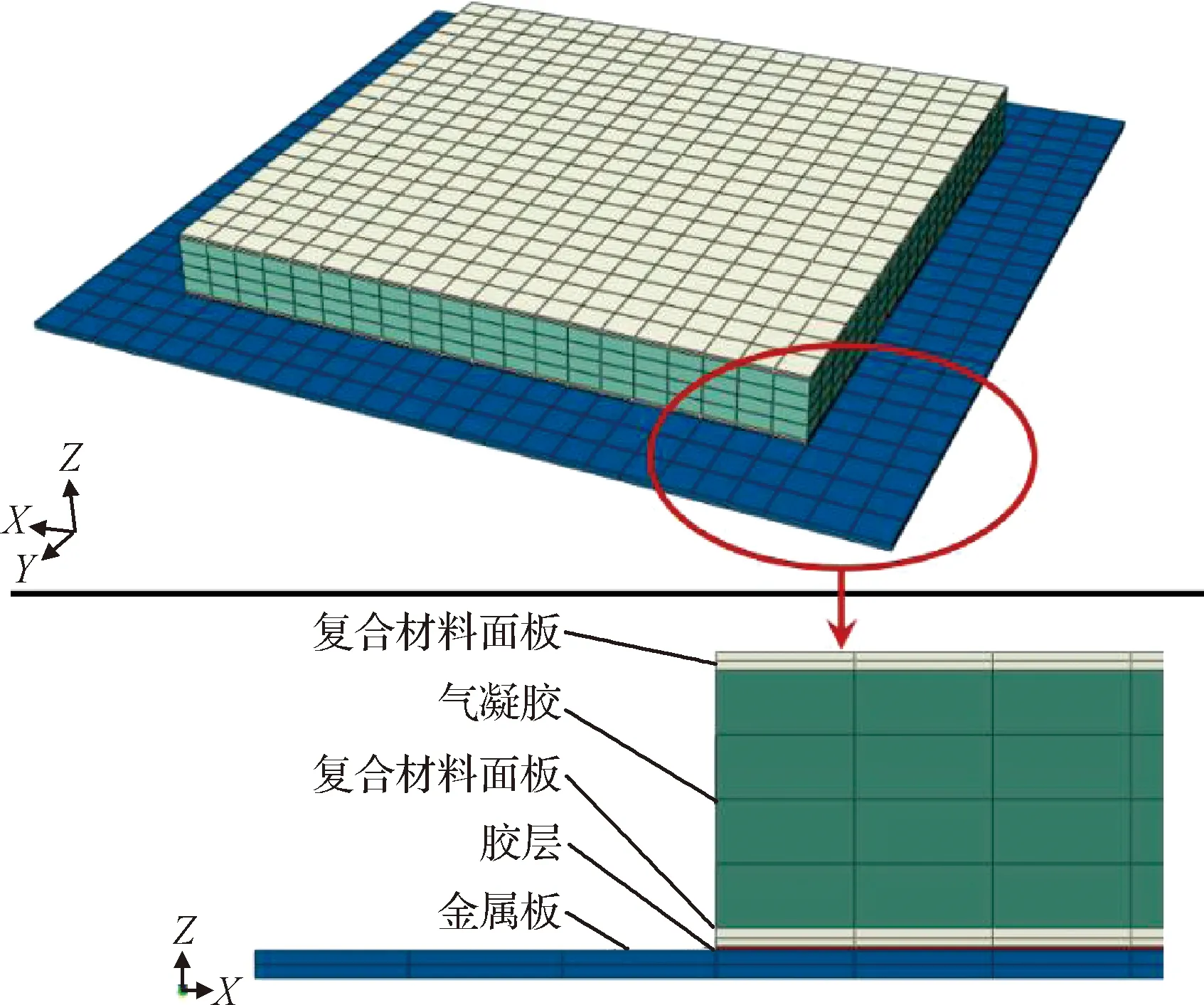
图7 夹芯式热防护结构有限元模型Fig.7 Finite element model of the sandwich thermal-protection structure

在实际工程应用中，其结构内部难以布置传感器，因此只能在其金属底板内侧布置传感器。其外表面受到空间上均匀分布的热流。以底部温度传感器获得的温度值，对外部热流载荷进行反演，获取结构外部施加的热流载荷。

当不考虑传感器的测量误差时，以底部金属板获得的数值仿真结果作为已知条件，反演其顶部输入热流，此时的热流反演平均误差为0.362 mW·mm。当使用不含噪声的温度测量数据反演时，热流的反演结果不会出现过拟合的情况，因此可以在设置收敛准则时设置一个较小的值，增加迭代次数。最终的反演结果能够很好的反映实际热流载荷。

在此基础上，考虑测量中由于传感器测量误差所造成的数据波动。分别在原模拟测量温度结果上加上方差分别为0.01、0.1,均值为0的正态分布随机误差。依据3σ准则，此两工况下误差分别在[-0.3 K, 0.3 K]与[-0.95 K, 0.95 K]之内。将模拟测量值进行降噪处理前后的结果分别用于反演其外表面所受热流，结果如图6所示。在考虑测量误差时，反演结果在整体的热流趋势上反演结果较好，但对于部分热流峰值的反演存在误差。

由表2可见，当不考虑传感器测量误差时，共轭梯度法能够有效地反演对复杂结构的热流载荷。而考虑传感器测量误差时，由于复合材料夹芯结构本身良好的隔热能力,温度传感器获取到的温度测量值较低,此时测量误差对于反演的结果有着很大的影响。因此，为了保证热流反演结果的精度，在布置传感器位置时应尽量选择温度较高的区域，以获取较大的灵敏度。

表2 含测量误差时热流反演平均误差Table 2 Average error in heat flux identification with measurement errors

3.3 再入飞行器结构热流反演

返回舱结构在再入大气过程中，与空气摩擦产生大量热量。本文以日本宇宙航空研究开发机构的PARTT返回舱结构为例展开研究，其结构如图8所示，分为返回舱主体、热防护结构、支撑结构和壳体四部分。并在结构内侧布置模拟传感器测点A与B，分别位于热防护结构的内侧与外侧。

图8 返回舱结构模型Fig.8 Structural model of the reentry capsule

对于复杂三维结构，由于其内侧各部分温差较大。在此采用不同位置的温度测量值作为输入，讨论测点位置对热流反演结果的影响。分别采用测点A与B的模拟测量结果作为输入，反演其所受热流载荷。反演结果如图9所示。当采用测点A的温度值作为反演输入数据时，热流反演平均误差为2.22 mW·mm;当采用测点B的温度值作为反演输入数据时，反演平均误差为1.30 mW·mm。

图9 测点不同时热流反演结果Fig.9 Identified results of heat flux with different sensor arrangement

由图9可见，当测点位置越靠近热流边界位置时，反演效果也越好。这是由于越靠近热载荷的位置，其结构温度越高，即灵敏度相对较高。此时误差相对于有效测量值的比例较低，测量误差对于反演结果的影响较小。因此在布置传感器时，需要尽量使其位置靠近热流边界。

在测点B处的结果上加上正态分布的随机误差模拟传感器的测量误差。分别加方差为1与2的误差，依据3σ准则,其误差所在区间分别为[-3 K, 3 K]与[-4.24 K, 4.24 K]。反演误差见表3，反演结果如图10所示。在考虑较大的测量误差下，热流反演结果与真实值相差较小，说明该反演方法具有良好的抗噪性。

表3 测量误差对热流反演结果的影响Table 3 Influence of measured error on the heat flux identification results

图10 不同测量误差时热流反演结果Fig.10 Identified results of heat flux with different measurement errors

4 结 论

本文针对再入飞行器结构开展热流载荷反演问题研究，采用共轭梯度法求解传热学反问题。在已知热流载荷作用区域和准确结构传热模型的基础上，通过结构内部区域布置的测温传感器反演了再入飞行器结构外部热流载荷变化过程。在此基础上探讨了材料热物性参数的温变特性、测点位置、传感器误差等因素对反演结果的影响，主要研究结论为：

1)共轭梯度法能够克服热流反演问题中的不适定性，可以较好地反演典型热防护结构和返回舱结构所受的热流载荷；

2)对于结构内部温度差异较大的结构，其热载荷反演过程中呈现出的非线性问题，通过修正灵敏度可以有效地提高识别精度。针对本文所研究的夹芯式热防护结构，考虑材料热物性为温变参数时，热流反演的平均误差从6.84 mW·mm降至3.88 mW·mm；

3)当反演复杂结构的热流载荷时，结构温度测点位置应尽量靠近主要入射热流位置，以提高计算中的灵敏度，从而提高反演精度。对于本文所研究的返回舱结构，当温度测点布置于热防护外侧时相比于测点布置于热防护结构内部，热流反演误差从2.22 mW·mm下降至1.30 mW·mm；

4)为了降低测量误差对反演结果的影响，需要采用合适的降噪手段并制定合适的收敛准则，从而防止反演结果出现过拟合。