卫星结构基础加速度激励及界面力识别试验研究

吴邵庆，尹 健，何子豪，何顶顶，陈树海

(1. 东南大学工程力学系，南京 211189；2. 东南大学江苏省空天机械装备工程研究中心，南京 211189；3. 上海卫星工程研究所，上海 201109)

0 引 言

当前卫星结构正朝着轻量化、高可靠性方向发展，对卫星整体及其部/组件在振动环境下的结构设计提出了更高要求。星-箭连接界面处的动载荷信息是卫星结构部/组件定量化设计的重要依据。发展星-箭结构界面力的高精度测量方法，对卫星整体结构及其部/组件的高精度定量化设计具有重要意义。

卫星界面力测量方法一般可分为直接测量和间接测量两种。直接在星-箭连接界面处布置力测量装置来获取界面力的方法会改变原有结构的动力学特征，一般只用于地面试验；发射段的界面力难以直接测量获取，常利用间接测量方法，这种方法也被称为载荷识别技术，其原理是基于结构模型构建激励与响应之间的传递关系，利用实测结构响应信号反演结构上的作用载荷。现有的界面力间接测量方法主要有两类。第一类是在星-箭连接环上粘贴应变片，利用星-箭连接环的理论模型和应变响应反演星-箭界面载荷；应变测量对主结构影响很小，方便实用；然而，由于该方法中使用了简化的理论模型模拟星-箭连接环,且应变响应对结构局部特征敏感，支撑连接环的隔板刚度对界面力识别的精度影响较大。第二类是利用星-箭结构有限元模型以及其上加速度响应来反演界面载荷；朱斯岩等采用Craig缩减动力学模型开展了由界面实测加速度响应识别星-箭界面载荷的仿真研究；尹健等利用卫星结构加速度响应和传递函数求逆法提出了星-箭连接界面处的环形分布动载荷识别方法，并开展了相关仿真研究。间接识别方法中，载荷识别结果精度依赖星-箭结构模型的精度。因此，高保真星-箭结构力学建模对界面力的准确识别尤为重要，有限元模型修正技术是获取高保真力学模型的重要方法。

现有基于结构响应的载荷反演技术主要专注于在获取了准确结构动力学模型的前提下发展新的动载荷识别方法，大多针对简单结构，在复杂卫星结构界面力识别中应用效果有待进一步研究，且界面力反演的试验研究极少。本文以某卫星结构模型为对象，开展了基于卫星结构实测响应识别基础加速度激励和星-箭连接界面力的试验研究。首先，为测量界面力，设计了卫星结构模型的力测量工装；其次，开展了自由和固定两种边界条件下的卫星结构模态试验和两阶段的模型修正，建立了卫星及其力测量工装的高保真动力学模型；最后，开展了卫星及其力测量工装的振动试验，利用实测卫星结构加速度响应反演基础加速度激励，并进一步将基础加速度激励施加于高保真卫星结构动力学模型求解界面力，利用力传感器测量得到的实际界面传递载荷验证识别结果的精度。论文的研究旨在为服役状态下的卫星结构振动载荷环境预测提供技术支持。

1 卫星结构模型与力测量工装设计

1.1 卫星结构有限元模型及连接参数化模拟

如图1所示,卫星结构由法兰盘、主承力筒、侧板、十字隔板、L型压条及M3螺钉连接件组成。构件材料和尺寸见表1。

图1 卫星结构模型Fig.1 Satellite structure model

表1 卫星结构主要构件尺寸Table 1 Dimensions of the main components in the satellite structure

建立卫星结构的有限元模型。结构上各部件采用六面体实体单元建模。采用等效线性化的薄层单元来模拟各部件之间的螺栓连接和接触，通过修正薄层单元的参数来准确模拟螺栓连接的力学行为，这种建模方法能在保证动力学模拟精度的同时提升分析效率。最终卫星结构有限元模型总共包含2003342个单元，14987622个自由度。

1.2 力测量工装设计

为测量振动试验中卫星结构所受到的激振力，设计了如图2所示的力测量工装，用于振动试验中振动台与卫星结构之间传递载荷的测量。

图2 力测量工装几何模型Fig.2 Force measuring tooling model

力测量工装中利用六个力传感器连接上方法兰盘和下方底座，底座通过M16螺栓与振动台台面连接。力传感器的量程根据卫星结构模型的质量以及基础激励加速度来确定。本研究中选用Maxwell A3D46三维力传感器。力传感器的选择需要保证力测量工装的刚度，使得工装底端固定在振动台时，基频大于卫星结构基频的5倍。力测量工装各部件的材料和尺寸见表2。建立力测量工装有限元模型，其中结构件和力传感器采用实体单元模拟，各螺栓连接和接触部位采用薄层单元模拟。将力传感器的等效材料参数和薄层单元参数作为有限元模型中的待修正参数。

表2 力测量工装材料及尺寸Table 2 Material and dimensions of the force measuring tooling

2 卫星结构高保真动力学建模

准确的动载荷识别结果依赖于高保真的结构动力学模型，因此在开展动载荷识别前，需要利用试验模态数据对建立的初始有限元模型进行修正，建立卫星结构的高保真动力学模型。利用单点测量、多点锤击的方法开展两阶段的模态试验：首先，开展自由悬吊状态下卫星结构的模态试验，获取结构的低阶自由振动模态；利用试验模态参数和基于灵敏度的有限元模型修正方法，获取能够准确模拟螺栓连接的薄层单元参数；进一步，将卫星结构及力测量工装组装并固定在振动台面上，开展固定状态下的卫星及力测量工装的模态试验，利用相同的模型修正方法获取力传感器结构的力学参数以及各接触部位螺栓连接的薄层单元参数。

2.1 自由模态试验与模型修正

选择基频低于试验结构基频1/5的弹性绳，用弹性绳将卫星模型倒挂，开展如图3所示的自由模态试验。所有模态试验的采样频率均为1000 Hz。在自由边界条件下测得卫星模型的前四阶整体模态，模态试验结果如图4所示。在自由边界条件下，卫星模型前两阶模态为对称的一阶弯曲振动模态，第三阶模态为一阶扭转振动模态，第四阶模态为整体纵向振动模态。由于加工误差等原因，两阶对称模态的固有频率存在一定偏差。

图3 卫星结构自由模态试验Fig.3 Free modal test of the satellite structure

图4 卫星结构自由模态试验振型图Fig.4 Mode shapes of satellite structure in free mode test

以自由模态试验的前四阶固有频率为修正目标，开展卫星结构有限元模型修正。修正参数主要包括：模拟螺栓连接的薄层单元弹性模量和泊松比。其中薄层单元根据描述的连接部位不同分为三类，上部立方体结构各构件之间、承力筒1与承力筒2之间、承力筒1与法兰盘之间的薄层单元分别定义为薄层单元1、2、3。开展各参数的灵敏度分析，选取灵敏度较大的参数作为待修正参数，进行迭代修正，参数初始值设定见表3，各参数的迭代收敛曲线如图5所示。图5(a)中给出了三种薄层单元弹性模量的迭代收敛曲线。薄层单元弹性模量初始值均设定为20 MPa，用于模拟界面间的接触。由于初值设定较小，不足以模拟各部件间实际的接触刚度，因此，随着迭代次数的增加，薄层单元1、2、3的弹性模量值均逐渐增大并分别收敛到15.3 MPa、630 MPa、630 MPa。图5(b)中给出了三种薄层单元泊松比的迭代收敛曲线。初始值均设定为0.3，从图中可以看出泊松比的收敛曲线由于薄层单元所模拟部位的受力特点不同而呈现两类不同形式。薄层单元1用于模拟上部立方体结构各构件之间的接触，泊松比收敛后在0.06和0.3之间振荡，表示薄层单元的剪切模量对上部立方体结构各构件之间的接触特征有影响，其影响在一定范围内波动；薄层单元2和3分别用于模拟承力筒1与承力筒2之间和承力筒1与法兰盘之间的接触，泊松比最后收敛到0.003，表示薄层单元的剪切模量对承力筒1与承力筒2之间和承力筒1与法兰盘之间的接触特性影响很小。模态频率在迭代过程中的误差收敛曲线如图6所示。从图中可以看出，自由状态下各阶模态固有频率值迅速收敛，收敛后曲线存在小幅振荡。自由模态试验状态下由于弹性绳悬挂边界条件等影响，待修正的各参数收敛后的数值呈现不同程度的小幅振荡，引起模态频率误差收敛曲线也存在类似现象。修正前后的模态频率与试验模态频率误差以及模态置信度(Modal assurance criterion, MAC)见表4，其中各阶主要振型MAC值匹配值分别为0.81、0.86、0.84，MAC值矩阵非对角元值均小于0.1。

表3 卫星有限元模型中薄层单元参数初始值Table 3 Initial values of thin-layer-element parameters in satellite’s finite element model

图5 卫星有限元模型上薄层单元参数收敛曲线Fig.5 Convergence curve of the thin-layer-element parameters on satellite’s finite element model

图6 自由边界下模态频率误差迭代收敛曲线Fig.6 Convergence curve of the modal frequency errors under free boundary condition during iteration

由表4中数据可知，修正后卫星模型的一阶弯曲、一阶扭转和一阶纵向模态的固有频率与试验频率误差均小于10%，修正后各振型匹配MAC值均大于0.8。值得注意的是，卫星结构模型具有对称性，一阶弯曲模态具有两个对称模态，两阶对称模态的固有频率计算值是完全相等的。由结果可知，修正后卫星有限元模型的计算模态参数与试验模态结果的匹配度较高，模型具有较高的精度。

表4 卫星有限元模型修正前后的模态参数与试验值对比Table 4 Comparison of modal parameters and experimental values before and after satellite finite element model updating

2.2 振动台固定模态试验与模型修正

将卫星结构通过力测量工装固定于振动台面，进一步开展底部固定工况下的模态试验。在固定边界条件下得到带力测量工装卫星结构的前四阶模态频率和对应振型，如图7所示。由图可知，在底端固定工况条件下，卫星结构及力测量工装的前两阶模态为对称的弯曲模态，第三阶模态为一阶扭转模态，第四阶模态为一阶纵向模态。试验中，两阶对称弯曲模态的固有频率会有一定偏差。

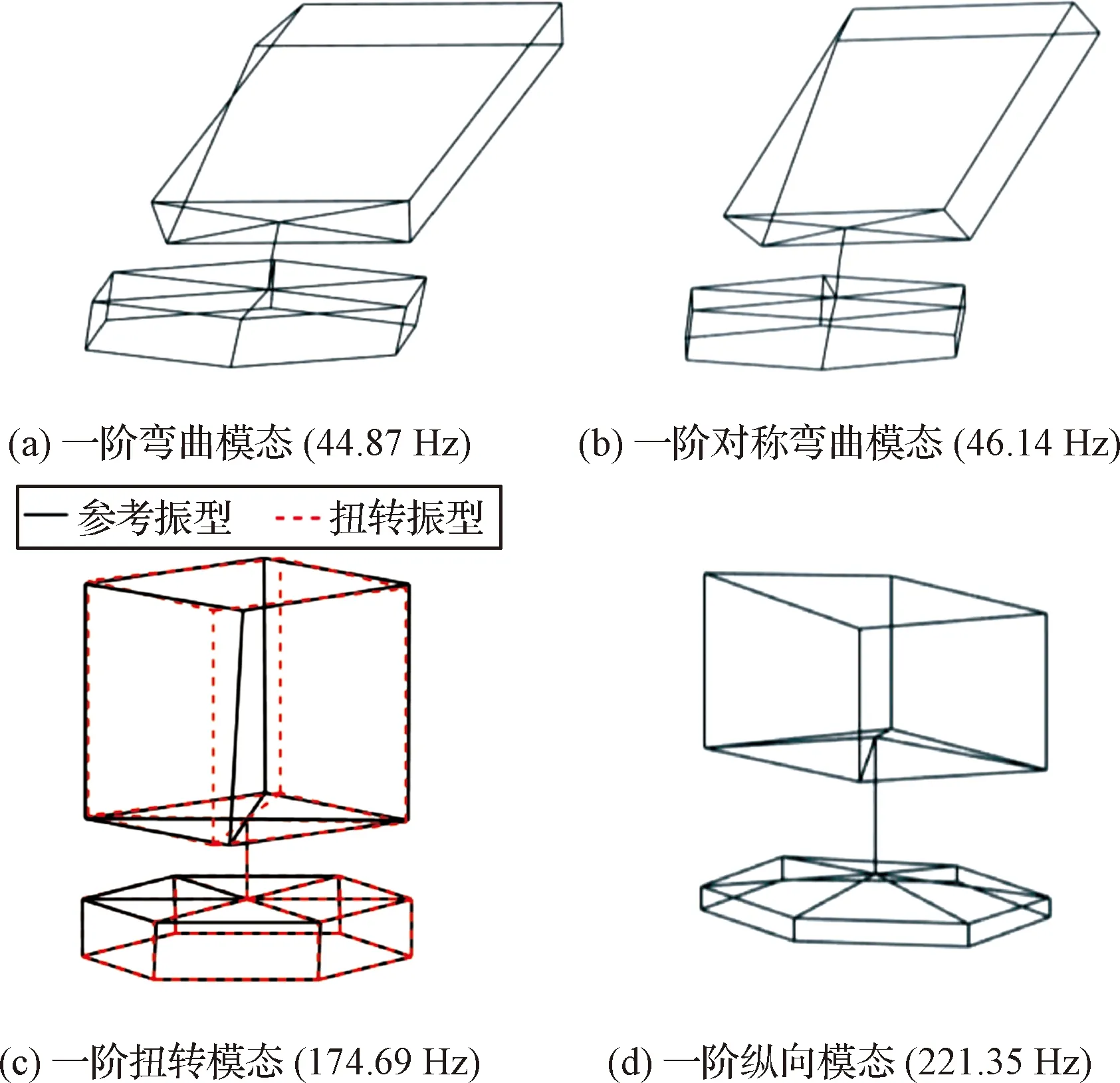
图7 底端固定带力测量工装卫星结构的试验模态振型图Fig.7 Experimental mode shapes of satellite structure with force measuring tooling under bottom-fixed scenario

在自由边界工况下的修正卫星结构有限元模型基础上，增加力测量工装的有限元模型，并以固定边界模态试验结果中的前四阶固有频率为修正目标，利用与2.1节中相同的方法开展模型修正。第二阶段模型修正参数包括力测量工装上模拟螺栓连接的各薄层单元及力传感器的弹性模量和泊松比。力传感器与法兰盘之间以及与工装之间的薄层单元分别定义为薄层单元4和5。力测量工装有限元模型薄层单元参数初始值见表5，各参数的迭代收敛曲线如图8所示。图8(a)中给出了薄层单元4和5的弹性模量迭代收敛曲线。初始弹性模量设定为20 MPa，薄层单元4的弹性模量随着迭代次数增加逐渐增大，最后收敛到69.6 MPa；薄层单元5的弹性模量随着迭代次数增加先增大后减小，最后收敛到18.1 MPa。可以看出，由于模型加工以及安装的误差等原因，力传感器与法兰盘之间和力传感器与工装之间的接触刚度并不一致，而薄层单元弹性模量较大表示较大的接触刚度。图8(c)中给出了薄层单元4和5的泊松比迭代收敛曲线，初始值取为0.1，随着迭代次数增加而增大，经过14次迭代分别收敛到0.34和0.35。图8(b)和(c)分别给出了力传感器等效弹性模量和等效泊松比的迭代收敛曲线，可以看出随着迭代次数增加，等效弹性模量和等效泊松比由初始值20 GPa和0.1逐渐增加并分别收敛到68.8 GPa和0.33。模态频率在迭代过程中的误差如图9所示。图9表明迭代过程中一阶弯曲模态所对应固有频率呈现先增后减，最后收敛的趋势，说明其受薄层单元4和5的弹性模量影响较大，而一阶纵向和一阶扭转模态对应于固有频率则呈现增大后收敛的趋势，受薄层单元4和5的弹性模量影响较小。修正前后的计算模态频率与试验模态频率误差见表6，其中各阶主要振型MAC值匹配值分别为0.95、0.94、0.88，MAC值矩阵非对角元值小于0.1。修正后模型的计算模态振型如图10所示。

图8 力测量工装模型中各修正参数收敛曲线Fig.8 Convergence curve of updating parameters in force measuring tooling model

图9 固定工况下模态频率迭代误差收敛曲线Fig.9 Convergence curve of modal frequency error under fixed scenario during iteration

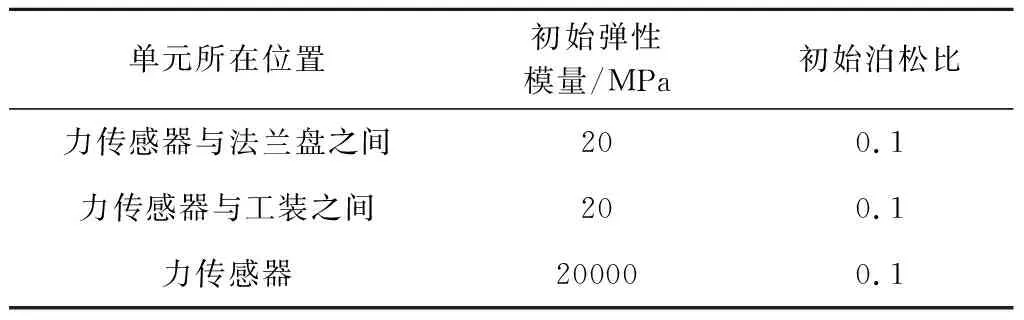
表5 力测量工装有限元模型薄层单元参数初始值Table 5 Initial values of thin-layer-element parameters in force measuring tooling’s finite element model

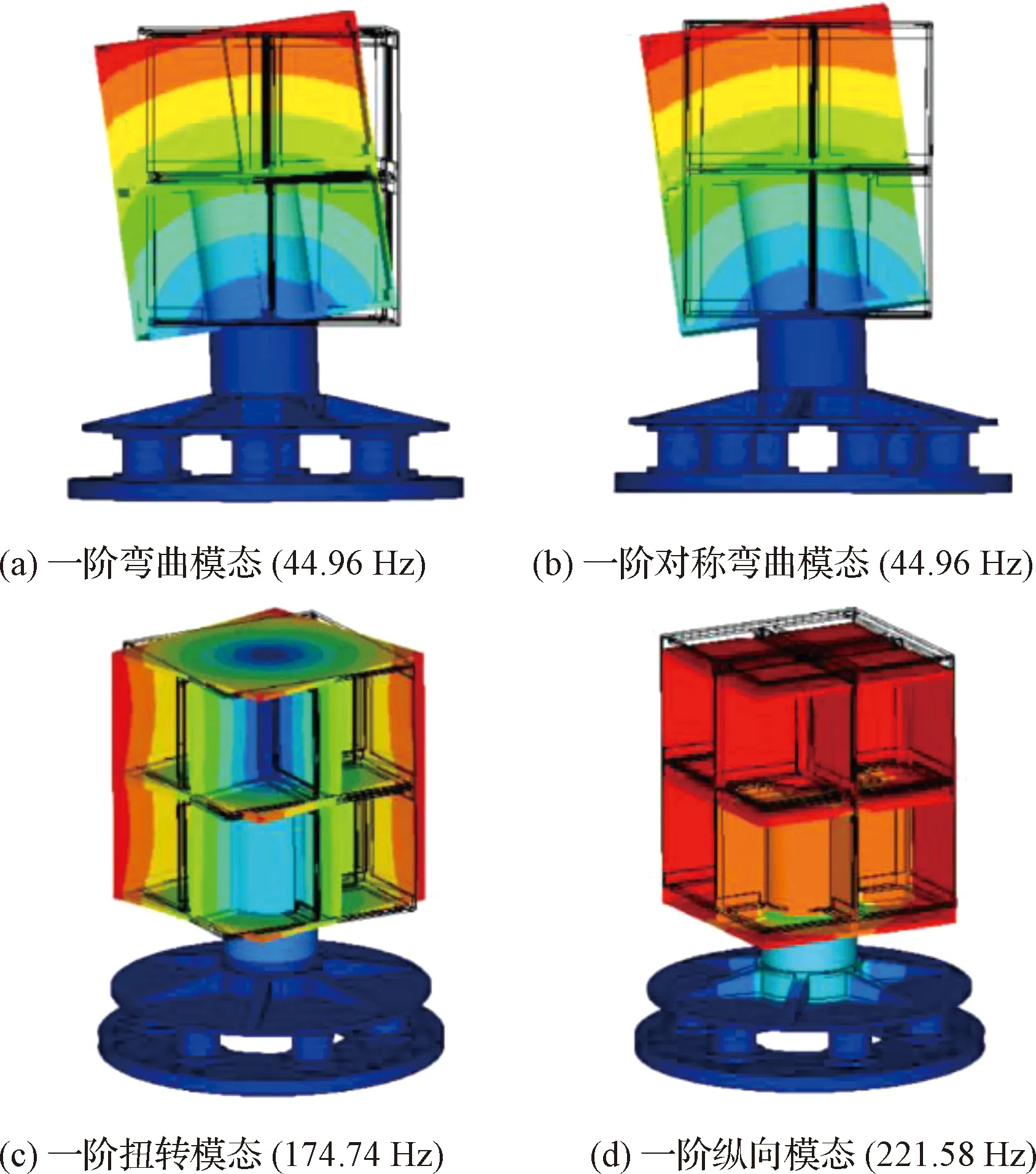
图10 底端固定工况下修正后结构的计算模态振型图Fig.10 Calculated mode shape diagram of the updated structure under bottom-fixed condition

由表6中的结果可知，修正后结构前四阶固有频率的误差均小于0.2%，振型MAC值的平均值大于0.9，修正后模型的主要低阶模态与试验结果吻合度非常高。底端固定工况下的模型修正进一步校准了力测量工装及其与卫星结构连接部位的有限元模型模拟精度，使得有限元模型能够高精度地表征结构的动力学特征，为后续的动载荷识别试验研究提供了带力测量工装卫星结构的高保真动力学模型。

表6 固定工况下修正前后的计算模态参数与试验值对比Table 6 Comparison of the calculated modal parameters and experimental values before and after updating under fixed scenario

3 振动台激振试验与基础激励反演验证

如图11所示，在底端固定的卫星结构模型上，利用三向加速度传感器测量卫星结构顶部以及振动台面的加速度信号，利用三向力传感器采集振动台与卫星结构间的传递载荷信号。基于实测结构加速度信号识别振动台基础激励和力测量工装上的传递载荷，并利用实测的振动台基础激励和力传感器测量载荷数据验证识别结果，完成试验研究。试验中共有6个加速度信号采集通道以及18个力信号采集通道。根据卫星结构所受激励的特点，利用振动台在水平方向施加频率为70 Hz，大小为0.5的正弦激励。

图11 卫星结构基础激励试验图Fig.11 Satellite structure base excitation test diagram

首先，基于格林函数矩阵求逆的基础加速度激励识别方法由实测卫星结构上测点1处的加速度反演振动台基础激励加速度，并与振动台面实测加速度对比。由算法可知，如果待识别的基础加速度激励为单一方向，最少只需构造一个识别方程，因此采用一个测点处的结构加速度响应信号即可满足要求。在载荷识别过程中，结构加速度响应中包含了振动台自身的固有频率信号以及测量噪声，如果将实测响应信号直接用于识别会引起激励识别结果的较大误差。利用信号滤波对实测结构加速度信号作了预处理，并将吉洪诺夫正则化方法应用于病态格林函数矩阵求逆，以提高激励识别的精度。识别结果取局部放大如图12所示。由图可知，识别的基础加速度激励时程曲线与实际施加的基础加速度时程曲线较为吻合，幅值误差较小，所识别的激振频率与试验值一致，但存在一定相位差。存在相位差的原因在于对实测结构加速度响应进行滤波处理时会影响其相位，进而引起基础加速度激励识别结果与实测值存在相位差。通过修正后卫星结构有限元模型识别的基础加速度激励与试验实测基础加速度激励的平均峰值误差为0.25 dB。

图12 振动台试验中基础加速度激励识别值与测量值对比Fig.12 Comparison between the identified and the measured base acceleration excitation values in shaking table test

进一步，将反演获得的基础激励施加于带力测量工装的卫星结构有限元模型，计算力测量工装处的传递动载荷时程曲线，并将计算得到的动载荷时程与力传感器实际测量时程进行对比，验证界面动载荷反演结果的精度。图13中给出了其中一个力传感器沿水平推力方向(向)，垂直水平推力方向(向)，竖直方向(向)的动载荷识别值与测量值在某一个时段内的对比结果。由图可知，识别得到的界面动载荷时程曲线与力传感器实测曲线吻合度较高，识别结果具有良好的精度。三个方向上的动载荷识别值与试验值峰值平均误差分别为1.53 dB、1.87 dB、2.14 dB。

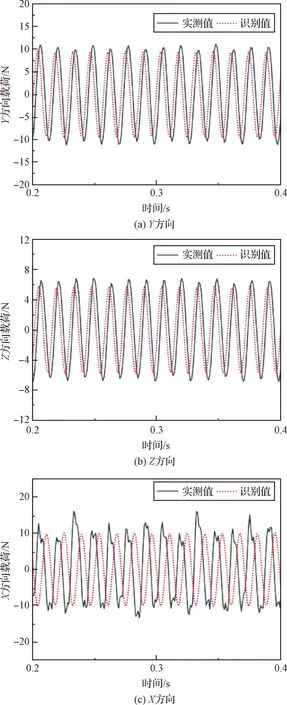
图13 识别动载荷时程与力传感器实测时程对比Fig.13 Comparison between the identified dynamic load time histories and the measured dynamic load time histories from force sensor

最后，由六个力传感器位置处的动载荷时程计算振动台与卫星结构之间传递的六自由度动载荷，验证界面传递六自由度载荷识别结果的精度。由于振动台加速度激励为沿方向的水平激励，六自由度载荷中，沿方向的水平合力与绕轴方向的弯矩为主要的载荷成份。图14中给出了，方向合力以及绕轴弯矩的识别值与试验参考值之间在某一个时段的对比结果。考虑所有力传感器的试验实测值,动载荷沿三个方向的合力时程曲线识别值与试验参考值峰值的平均误差分别为1.58 dB、1.77 dB和2.40 dB。由此可知，利用动载荷识别方法开展星-箭连接界面处传递动载荷的反演具有较好的精度；在水平激励下，由单点实测加速度激励即可实现整个界面上的六自由度动载荷识别，在实际工程应用中具有重要的应用价值。当存在多个方向的线振动和角振动时，可以通过增加测点的方式解决更为复杂振动激励下的六自由度动载荷识别问题。

图14 力传感器处六自由度载荷部分识别值与实测值对比Fig.14 Comparison between the partial identified and measured values of 6 DOF load at force sensor

4 结 论

论文以某卫星结构模型为研究对象，开展基于实测卫星结构加速度的振动台基础加速度激励和星-箭界面动载荷识别的试验研究。为保证基础加速度激励和界面动载荷识别的精度，开展了卫星结构模型的有限元建模和基于试验模态数据的模型修正，得到了能够准确反映其动力学特性的高保真有限元模型，并进一步结合格林函数求逆法和高保真结构有限元模型，由实测结构加速度响应识别了基础加速度激励和界面传递动载荷。研究表明：1)基于薄层单元的螺栓连接模拟方法应用于复杂卫星结构的有限元建模具有方法简单、计算高效等优点，配合多阶段的模型修正技术能够获得高保真的卫星结构动力学模型；2)在保证结构有限元模型精度的前提下，卫星基础加速度激励和界面动载荷的识别结果也具有较好的精度。

论文仅开展了单个方向基础加速度激励和相关界面力的识别，文中只采用了单个加速度传感器测量得到的结构加速度信号,如多个方向的线振动和角振动同时激振，则需要增加测点以构造更多的识别方程，解决多方向多形式振动激励下的六自由度动载荷识别问题。