运载火箭推力故障下在线计算轻量化任务重构方法
何 骁,谭述君,2,吴志刚,张立勇,刘玉玺
(1.大连理工大学工业装备结构分析国家重点实验室,大连 116024; 2.大连理工大学辽宁省空天飞行器前沿技术重点实验室,大连 116024;3. 大连理工大学电子与信息工程学院,大连 116024; 4.上海宇航系统工程研究所,上海 201109)
0 引 言
根据1980年至2004年世界航天器发射故障统计,推进系统故障占绝大多数。其中,美国31次发射失败中有16次是由推进系统故障引起的,俄罗斯65次发射失败中有37次是由推进系统故障引起的。近年来,推进系统故障中推力下降故障依旧不断,如2017年LM-5/Y2发射、2012年Delta 4发射和2012年SpaceX Falcon 9发射。当发动机发生推力下降故障时,跟踪地面设计的标称弹道是不可行的。我国的运载火箭的动力系统余量较小,推力下降故障会导致到目标轨道无法到达。为了解决运载火箭因推力下降故障而坠毁的问题,需要研究一种在线任务重构方法,或叫飞行任务降级方法,来求解最优救援轨道对应的飞行轨迹(最优轨迹)。
一般来说,求解航天器轨迹优化问题的主流方法是数值法,可分为直接法、间接法。由于直接法求解效率高,在航天器轨迹优化问题中得到了更多的应用。因此有学者用直接法来研究火箭推力故障下的轨迹规划问题。文献[10]提出了一种状态触发指标法(State-triggered indices, STI),解决了运载火箭推力下降时目标轨道和飞行轨迹的在线联合优化问题。在文献[11]中,利用凸优化方法,将原来的非凸优化问题转化为一种凸问题在线优化。文献[12]设计决策等级以确定任务目标,结合目标轨道根数的约束情况,采用自适应伪谱法规划出满足要求的飞行弹道。然而,在线用直接法求解任务重构问题存在在线求解计算消耗大的问题。计算消耗大主要体现在:1)在线计算需依次求解多个优化问题,能量高的轨道的最优轨迹求解依赖于能量低的轨道;2)轨迹优化问题的初值与最优解的偏差较大,迭代计算收敛慢。
近年来,随着机器学习技术的发展,将机器学习技术与传统的航天器研究方法结合是一大研究趋势。其中机器学习技术中的监督学习、强化学习在改进轨迹规划算法方面很有潜力。文献[17]提出了一种通过强化学习训练导弹制导律的新方法,与比例制导律相比,该制导律对控制器模型具有更好的鲁棒性。然而,由于需要与环境交互,强化学习的计算负担往往会影响在线应用的可行性。利用监督学习技术,在预先产生的数据集上训练神经网络,生成轨迹或导引律是一个可在线应用的方案。文献[19]提出了一种基于神经网络的非线性混合算法,在降低复杂度和成本的前提下为控制、制导系统提供反馈。文献[20-21]提出了基于径向基神经网络救援轨道决策的轨迹重规划方法,该方法可快速预测出救援轨道。径向基函数神经网络(Radial basis function neural network, RBFNN)是一种监督学习方法,在函数逼近中具有良好的非线性映射能力。与标准前向反馈传播的BP网络相比,RBFNN具有学习速度快、陷入局部极小点可能性小等优点。
针对在线计算轻量化的任务重构问题,本文提出一种基于径向基神经网络轨迹决策的在线任务重构方法。与传统的航天器轨迹优化方法不同,提出的方法在线应用时,不需要基于动力学模型迭代求解,只需将离线训练好的神经网络迁移到在线应用,即可快速决策最优救援轨道对应飞行轨迹的近似解。
1 问题描述
1.1 推力下降故障下的动力学方程
以两级运载火箭为研究对象,假设推力下降故障发生在二级飞行段。定义地心惯性坐标系:原点在地心,轴在赤道平面内指向发射时刻本初子午线方向,轴垂直赤道平面指向北极,轴满足右手定则。在地心惯性坐标系中建立火箭的上升段二级飞行动力学方程如下:

(1)

(2)
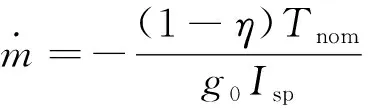
(3)
式中:=[,,],=[,,]为运载火箭的位置、速度向量;为地球引力常数;是火箭的总质量;为火箭的发动机比冲;=[,,]为发动机的推力单位矢量在地心惯性坐标系中的分量,是可控的;当发动机发生故障,推力下降的比例是,推力大小是(1-),是发动机标称推力;假设发动机比冲不变,若推力下降的比例是,那么推进剂的秒耗量下降;是海平面上的重力加速度。下文所有计算都是以式(1)~(3)作为状态方程,包含7个状态量=[,,]和3个控制量=[,,]。
1.2 任务重构问题
传统的运载火箭轨迹优化是一个最优控制问题,优化飞行轨迹使得运载火箭进入确定的目标轨道。然而,当推力下降故障严重时,运载火箭无法进入目标轨道。这种情况下,为了避免运载火箭坠入大气层,需要解决一个没有确定目标轨道的飞行任务重构问题。
在任务重构问题中,救援轨道和飞行轨迹同时被优化。任务重构问题的目标函数可表示为五个轨道要素绝对偏差的加权和,优化问题可表示为问题0,如下所示:

(4)

1.3 目前的任务重构问题求解策略
在问题0的目标函数中,由于轨道平面元素(,)和轨道形状元素(,,)之间的矛盾,导致解的搜索方向发散或搜索步长减小,从而大大降低了求解效率。文献[10]提出了一种状态触发指数(STI)策略来求解问题0,在STI策略中,从安全的角度出发,保证轨道高度是优先考虑的,只有当剩余运载能力大于某一阈值时,才考虑对轨道平面进行调整。参考STI策略,本文根据救援轨道的类型将问题0转化为两个子问题。
在故障较严重但非致命的情况,为保证救援轨道的高度,优先考虑提高轨道高度。即在故障发生时,寻找当前时刻同一轨道平面上的最高圆轨道。在这种情况下,问题0可转化为寻找最高圆救援轨道的最优控制问题1,如下所示:

(5)
其中,是弹道倾角,是飞行的总时间。用两个等效的终端约束代替=0,以减小位置、速度与轨道根数转换函数的非线性。两个等效终端约束的物理意义是弹道倾角等于0,重力提供向心加速度。
如果问题1的轨道高度大于目标轨道的近地点高度,则表明可以使用一定量的推进剂来减小轨道平面偏差。在这种情况下,在保持轨道高度的同时,调整轨道倾角和升交点赤经,问题0可转化为寻找最优椭圆救援轨道的优化问题2,如下所示:
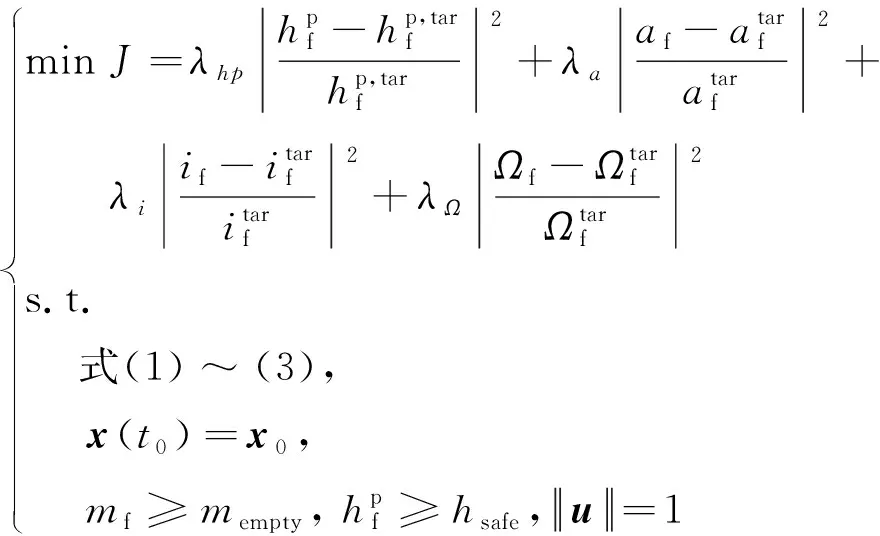
(6)

综上所述,原任务重构问题0转化为问题1和问题2,如图1所示。
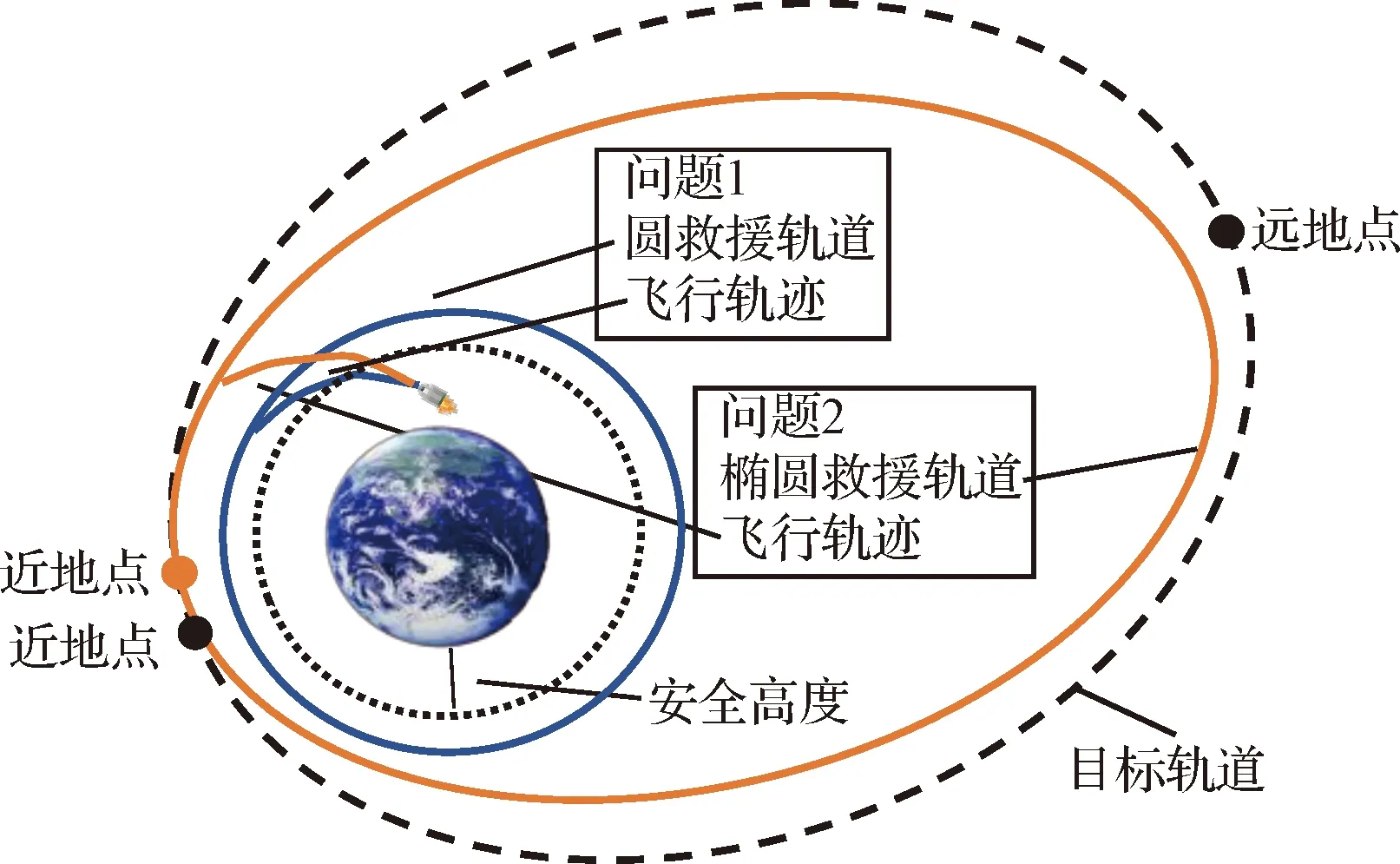
图1 任务重构的示意图Fig.1 Schematic of mission reconstruction
采用航天器轨迹优化的直接法,如自适应配点法或其改进方法,依次求解问题1和问题2可解决任务重构问题。然而,这种序列求解多个优化问题的策略有在线计算消耗大的问题。计算消耗大主要体现在:1)问题1和问题2的入轨轨道未知,很难设置合适的初始猜测值,这导致问题1和问题2求解计算消耗大;2)问题2飞行轨迹求解依赖于问题1轨道的飞行轨迹,需在线依次求解多个优化问题,这进一步增大了在线的计算消耗。
2 在线计算轻量化的智能任务重构方法
为了解决运载火箭推力故障下任务重构在线计算消耗大的问题,本文引入神经网络技术,采用离线学习“故障状态-最优轨迹”动力学关系,再迁移到在线决策最优轨迹近似解的策略,提出了一种在线计算轻量化的任务重构方法。整个任务重构方法的策略如图2所示。在离线部分,遍历大量的故障状态,采用凸优化与自适应配点法离线求解轨迹优化问题1和问题2,建立“故障状态-最优轨迹”数据集。以数据集为基础离线训练径向基神经网络,建立轨迹决策模型。在线部分,将轨迹决策模型迁移到在线应用,以实际飞行的故障状态作为输入,在线决策最优轨迹。与基于动力学模型迭代求解的方法相比,本文方法避免了在线求解一个难以构造合适初值的优化问题。同时,本文求解策略可直接获得最优轨迹的近似解,避免了一系列子问题的求解过程。

图2 在线任务重构策略Fig.2 Online mission reconstruction strategy
2.1 数据集产生
神经网络是通过训练来学习数据集中的知识与规律,数据集中轨迹的正确性必须要保证。为了获得最优的救援轨道与飞行轨迹,凸优化与自适应配点法结合的方法(Convex optimization and adaptive collocation method, CAC method)被用来求解问题1和问题2,以生成轨迹集。CAC方法是STI策略中采用的一种对救援轨道和飞行轨迹联合求解的方法。凸优化具有收敛性好,且不会陷入局部最小值的优点。采用凸优化的解提供初值,可保证数据集中轨迹的最优性。由于问题1和问题2轨迹的分布差异较大,将问题1和问题2的解保存到两个数据子集中,分别为数据子集1、数据子集2。
发生故障前,如果运载火箭能准确跟踪标称弹道,那么推力下降的大小、发生推力故障的时刻足以描述所有故障模式。实际飞行中,由于存在噪声干扰,火箭的位置、速度在标称弹道附近。为了更全面的描述故障,故障状态的特征是故障发生的时间、推力下降的比例、故障时的状态变量(位置、速度、质量)。


图3 数据集的求解流程图Fig.3 Flow chart of solving datasets


2.2 轨迹决策模型建立与训练
径向基神经网络(Radial basis function neural network, RBFNN)被用来决策最优轨迹近似解。RBFNN是一种局部逼近网络,通常由输入层、隐藏层、输出层三层网络构成。理论上,具有足够多隐层神经元的径向基神经网络能以任意精度逼近任意连续函数。
隐藏单元由基函数激活,本文采用高斯基函数,第个隐藏层的输出为:

(7)

输出层对径向基函数隐藏层的输出进行线性组合以生成预期的输出。输出层第个节点的输出为

(8)
式中:为第个隐层神经元到第个输出神经元的权重,为隐层神经元的数量。正交最小二乘法(Orthogonal least-squares, OLS)被用来训练径向基神经网络。OLS是一种由Chen等提出的一种选择RBFNN数据中心的方法,训练的网络规模小,隐藏层采用少量的神经元节点就能映射非线性关系。OLS形式的径向基神经网络中神经元数量参数较少,神经元连接权重参数也少。因此迁移到在线应用的神经网络模型占用的存储空间小,神经网络正向传播的计算消耗也少,适合用于轨迹决策。


图4 轨迹决策神经网络Fig.4 Neural network of trajectory decision-making
2.3 在线轨迹决策


图5 轨迹决策的示意图Fig.5 Schematic diagram of trajectory decision-making
3 仿真校验
在本节中,以运载火箭的二级飞行阶段为研究对象,发射参数见表1。地球引力系数设为3.986×10m/s,假设地球是一个均匀的球体,地球半径是6378140 m。第二阶段上升阶段为真空环境,其中是发动机比冲,海平面重力加速度设为9.8 m/s。

表1 发射参数Table 1 Launcher parameters
表2给出了地心惯性坐标系中的第二阶段初始状态。目标轨道的近地点和远地点高度分别为200 km和300 km。目标轨道的轨道要素见表3。安全轨道高度=160 km。

表2 二级的初始状态Table 2 Second stage initial states

表3 目标轨道的轨道根数Table 3 Target orbital elements
本文的数值仿真都是在英特尔酷睿i7-7700 CPU 3.60 GHz电脑上进行的,MATLAB版本为2018b。自适应配点法所采用的配点是正交Legendre多项式的零点。
3.1 数据集产生
因为标称情况下,二级段飞行时间是378 s。如果推力下降比例低于12%时,采用迭代制导仍然可以到达目标轨道,不需要在线任务重构。数据集的故障发生时间是0~378 s,步长为0.5 s;推力下降大小12%~30%,步长为0.1%。取值依据具体的飞行任务,本算例中近地点和远地点高度分别为200 km和300 km,Δ取5 km。在问题2中优先调整轨道平面,目标函数权重,,,取值10,10,10,10。数据子集1中共18494个圆救援轨道类型样本,数据子集2中有9350个椭圆救援轨道类型样本。在数据集中,随机抽取90%的数据作为训练集,剩余10%的数据作为测试集。
3.2 蒙特卡洛仿真
为了验证算法的正确性与在线计算效率的先进性,采用本文提出的方法和文献[10]的CAC方法求解在线任务重构问题。采用本文方法与CAC方法求解这些故障下的任务重构问题,用来对比验证本文方法的精度与在线计算的效率。文献[10]未明确说明自适应配点法的自适应规则与配点设置,本文CAC方法的复现工作采用经典自适应配点法。
..决策精度验证
为了验证轨迹决策的准确性,在测试集上仿真了本文方法决策的轨迹与CAC方法计算出的轨迹,并统计这两个方法结果的误差。轨迹中状态量的误差用所有时间节点上状态量的平均绝对误差(Mean absolute error, MAE)来刻画,其表达式为

(9)


(10)
误差采用盒状图表示,如图6所示。盒状图是一种统计数据分布的可视化方法,单个盒状图从下往上分别是数据的下限、下四分位数、中位数、上四分位数、上限。
数据子集1用来训练圆轨道救援的轨迹决策神经网络,径向基宽度是1,最终训练好的隐藏层神经元数量是100。圆轨道救援类型结果中的位置、速度、控制变量在测试集上的误差如图6(a)~(c)所示。可以看出,75%的位置误差在100 m以内,位置误差的上限是500 m。75%的速度误差在0.2 m/s以内,速度误差的上限是1.4 m/s。75%的控制变量误差在5×10以内,控制变量的上限是2.5×10。

图6 轨迹决策的误差Fig.6 Errors of trajectory decision-making
数据子集2用来训练椭圆轨道救援的轨迹决策神经网络,径向基宽度是1,最终训练好的隐藏层神经元数量是100。椭圆轨道救援类型结果中的位置、速度、控制变量在测试集上的误差如图6(d)~(f)所示。椭圆轨道救援轨迹决策的位置、速度与控制变量误差比圆轨道救援类型的大。这是因为椭圆轨道救援的优化问题中,目标函数包含多个变量,故障状态与最优轨迹的非线性关系更复杂。
通过统计、分析本文方法决策的轨迹与CAC方法计算出的轨迹之间的误差,验证了本文方法在多种圆、椭圆轨道救援情况下轨迹决策的误差小,建立的轨迹决策模型泛化能力强。
..在线计算时间对比验证
为了验证本文算法在线计算时间的先进性,仿真对比了本文方法和CAC方法的在线计算时间。为了绘图的清晰,图7和图8分别展示了100个故障对应的在线计算时间,这100个故障是在测试集中随机抽取的。

图7 在线任务重构CPU耗时(圆轨道)Fig.7 CPU time consuming of online mission reconfiguration (circular orbit)

图8 在线任务重构CPU耗时(椭圆轨道)Fig.8 CPU time consuming of online mission reconfiguration (elliptical orbit)
图7显示了本文方法与CAC方法在求解问题1的在线计算时间比较。与CAC方法相比,采用本文方法,在线任务重构的平均计算时间由1.06 s降至0.007 s。本文方法的平均计算时间比CAC方法节省了99.3%。
图8显示了本文方法与CAC方法在求解问题2的在线计算时间比较。与CAC方法相比,采用本文方法在线任务重构的平均计算时间由6.253 s降至0.006 s。本文方法的平均计算时间比CAC方法节省了99.9%。此外,图8中CAC方法在不同故障下的计算时间数量级差别大。这是因为椭圆情况下优化问题的初值敏感性高,自适应配点法在结果不满足精度的情况下,自适应地增加了配点,导致计算成本增长,计算时间变长。由此可见,本文提出的基于轨迹智能决策的在线任务重构方法显著地缩减了在线部分的计算时间。这是因为本文方法将离线训练好的神经网络迁移到在线应用,在线部分只需计算神经网络的正向传播,是简单的矩阵相乘、相加运算。航天器轨迹优化的直接法是基于动力学模型离散原问题,再利用迭代的方法去求解。而本文方法在线部分的计算无需迭代计算,有着更少的计算成本,因此在线计算时间更少。此外,本文方法的所有测试仿真的时间都在一个量级,计算时间更稳定。
3.3 算法的鲁棒性分析
为了分析本文算法重构的救援轨道与飞行轨迹的鲁棒性,在两种典型故障状态下,做了本文方法与文献[10]的CAC方法在不同工况下的仿真。由于飞行过程中存在不确定性的影响,运载火箭距离标称轨迹有一定的误差。因此,为了验证方法的鲁棒性,假设故障发生时刻的位置、速度有偏差。
在运载火箭二级飞行段,火箭的位置在地心惯性坐标系轴的变化少,分别设置正、负不确定性为:Δ=[5,05,5]km,Δ=[5,5,5]m/s,图例中表示为“+5 km,+5 m/s”;Δ=[-5,-05,-5]km,Δ=[-5,-5,-5]m/s,图例中表示为“-5 km,-5 m/s”。
假设在第二级飞行阶段,推力在110 s时减少25%。这种故障下的任务重构问题属于问题1,本文方法与CAC方法在不同工况下的结果如图9、图10和表4所示。图9是海拔高度曲线,图10是速度曲线。无偏差情况下,本文方法与CAC方法规划出的轨迹结果一致。存在偏差的情况下,本文方法与CAC方法的轨迹结果很接近。本文方法与CAC方法在线求解的救援轨道见表4。表4中几种工况下,救援轨道的偏心率是0,表示是圆救援轨道,而轨道倾角、升交点赤经为发生故障时的值,从而最大程度地利用推进剂能量来提高轨道高度。
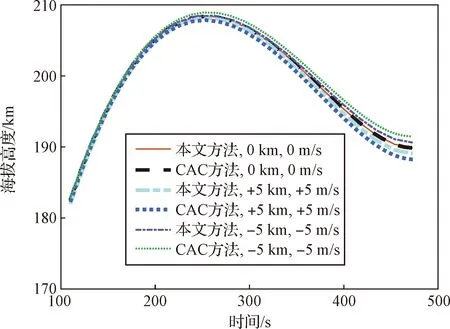
图9 海拔高度曲线(圆轨道)Fig.9 Altitude curve (circular orbit)

图10 速度曲线(圆轨道)Fig.10 Speed curve (circular orbit)

表4 入轨点轨道根数(圆轨道)Table 4 Orbital elements of injection point (circular orbit)
若推力在144.5 s下降25%,这种故障下的任务重构问题属于问题2,本文方法与CAC方法在不同工况下的结果如图11、图12和表5所示。

图11 海拔高度曲线(椭圆轨道)Fig.11 Altitude curve (circular orbit)
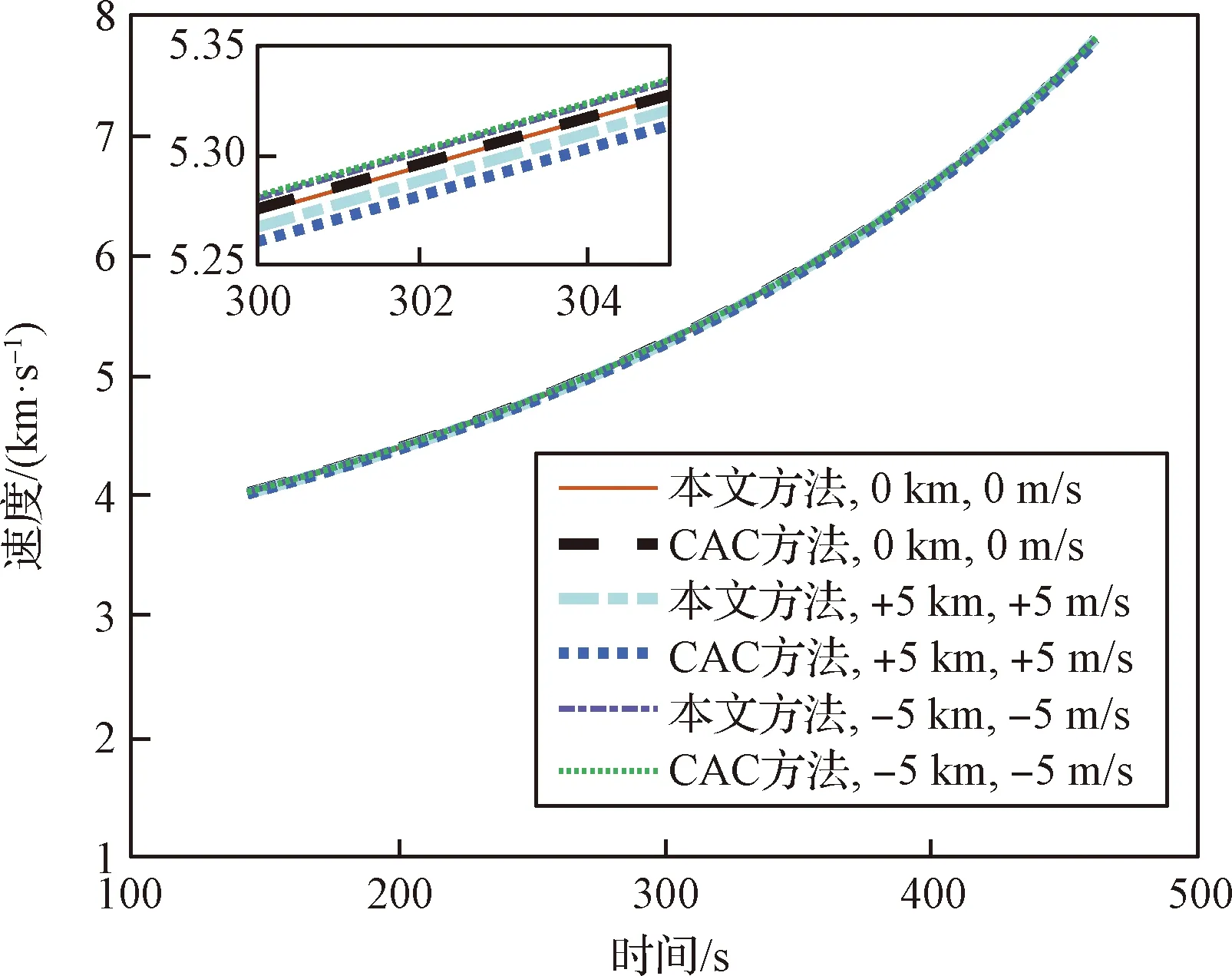
图12 速度曲线(椭圆轨道)Fig.12 Speed curve (elliptical orbit)

表5 入轨点轨道根数(椭圆轨道)Table 5 Orbital elements of injection point (elliptical orbit)
与问题1的结果类似,无偏差情况下,本文方法与CAC方法规划出的轨迹结果一致。存在偏差的情况下,本文方法与CAC方法的轨迹结果很接近。
因此,本文提出的基于轨迹智能决策的任务重构方法可以获得推力故障下任务重构问题近似最优解,并对于初始位置、速度的偏差有一定鲁棒性。
4 结 论
针对运载火箭推力下降故障下任务重构问题的在线计算轻量化需求,采用径向基神经网络离线学习“故障状态-最优轨迹”动力学关系,再迁移到在线应用,提出了一种基于轨迹智能决策的任务重构方法。得到如下结论:
1)通过“故障状态-最优轨迹”数据集训练径向基神经网络可得到轨迹决策模型,该模型能决策出近似最优的轨道与对应的飞行轨迹。此外轨迹决策方法对于初值点的位置、速度偏差有鲁棒性。
2)提出的基于轨迹智能决策的任务重构方法具有在线计算时间短、计算时间稳定的特点。与目前的轨迹优化方法CAC相比,对于圆、椭圆轨道救援类型,本文方法的平均在线计算时间减少了三个数量级,且本文方法的仿真计算时间均稳定在0.01 s以内。
上述结论表明,本文提出的基于轨迹决策的在线计算轻量化的任务重构方法可显著提高在线计算的效率、增强发射的可靠性,有很强的工程应用前景。

