嫦娥五号平动点拓展任务轨道方案研究

刘 磊，刘 勇，陈 明，谢剑锋，马传令

(北京航天飞行控制中心航天飞行动力学技术重点实验室，北京 100094)

0 引 言

2020年11月24日中国成功发射嫦娥五号(CE-5)月球探测器，并于12月17日成功回收CE-5返回器，实现了1976年苏联月球采样任务后人类再次获取月壤样品，同时标志着中国“绕落回”月球探测工程任务圆满结束，并成为美俄之后成功实施月球采样返回的国家。CE-5探测器采样返回时由返回器和轨道器组成，在探测器到达地球附近预定高度后，返回器和轨道器分离，返回器返回着陆场，轨道器则经过控制后进入地心大椭圆轨道。在轨道器状态良好的情况下，可以开展拓展飞行任务以实现对任务资源的最大利用，尤其为后续月球和深空探测任务探索关键技术和积累任务经验。

类似于中国月球探测再入返回飞行试验任务(嫦娥5T1)，受探测器状态和能力约束，CE-5轨道器拓展任务飞行范围选择日地和地月空间较为适宜。进一步，考虑到日地和地月平动点对深空探测任务具有重要应用价值，如日地L1点是对太阳和宇宙射线以及地磁场研究的绝佳位置，地月平动点可为地月空间尤其是月球附近的航天器提供稳定的导航和中继通信等任务支持，以及可作为未来月球自动采样返回和深空探测任务的转移中枢。因此，文章选择日地和地月平动点作为CE-5拓展任务的飞行目标，研究利用轨道器开展平动点拓展任务，设计相应的平动点轨道及其转移轨道，提出多个飞行控制方案供任务总体选择决策，其中包括应用广泛的日地Lissajous轨道、尚未开发应用的地月Lyapunov轨道、美国“深空门户”空间站拟采用的地月NRHO轨道等。

1 轨道动力学模型

CE-5平动点拓展任务设计采用两种轨道动力学模型：圆型限制性三体问题(CR3BP)模型和精确力模型。

1.1 CR3BP模型

设探测器质量为，两个大天体的质量分别为和，且有≪<。以和的共同质心为原点,绕的运动平面为惯性坐标系的平面，相对于运动的近拱点方向为轴指向，建立惯性坐标系-和会合坐标系-，如图1所示。

图1 CR3BP的惯性坐标系和会合坐标系Fig.1 Inertial and synodic coordinate system of CR3BP

选择质量单位为+，长度单位为绕运动的半长轴，时间单位为运动角速度的倒数，记=≤12，下文中地月系取0.01215，日地系取3×10，则探测器在-中的运动方程为

(1)

其中

(2)

在CR3BP下，三体系统存在3个共线平动点和2个三角平动点，且由式(1)可推导得到共线平动点附近线性运动的周期解为

(3)

式中:和分别是平动点轨道在和方向的运动幅值;和分别为和方向的相位角，二者相等时即Halo轨道;和分别为和方向的运动频率，与参数一起由三体系统确定。

1.2 精确力模型

CR3BP模型与真实力学环境存在一定偏差，因此需要采用含摄动因素的精确力模型修正设计轨道。与近地航天器相比，平动点轨道的精确力模型仅需考虑大天体引力和太阳辐射压等主要摄动因素即可满足任务设计需求。

1)大天体引力

轨道计算时一般选择较大的天体作为中心天体，建立惯性坐标系和动力学方程，如太阳系内选择太阳作为中心天体，太阳或太阳系质心作为惯性坐标系原点，地月系内则选择地球作为中心天体，地心作为惯性坐标系原点。

设全部大天体总数为，中心天体编号为1，其余天体编号为(=2,…,)，平动点探测器相对于中心天体和其余天体的位置矢量分别为和，则平动点探测器相对于中心天体的加速度为

(4)

2)太阳辐射压

对于太阳系内的平动点轨道，太阳辐射压是除大天体引力外最大的摄动力，也是导致平动点轨道自然漂移的最大摄动因素。

对于形状简单的探测器，太阳辐射压产生的加速度为

(5)

其中，为探测器表面反射系数;为垂直于辐射方向的探测器截面积;为探测器质量;AU=149597870 km,为AU处的光压通量;为光速;为从太阳到探测器的位置矢量;为阴影系数，平动点轨道设计时忽略阴影影响。轨道设计阶段,取1.2，取299792.458 km/s，取1。实际任务中，利用精确跟踪测量数据进一步精确估计和等参数。

对于形状复杂的探测器，可以将航天器表面分解处理的方法，相应计算较复杂，对于平动点轨道设计而言，式(5)即可满足一般需求。

此外，平动点轨道研究有时也采用双圆限制性四体问题模型，如日地月和探测器组成的双圆限制性四体问题,即考虑日地月质点引力、地月和日地月分别绕各自共同质心做圆周运动，其动力学精度介于上述两种力模型之间，综合计算精度和效率，本文未采用该模型。

2 拓展任务轨道设计

在利用月球探测器开展平动点拓展任务方面，2011年6月中国成功实施了嫦娥二号日地平动点拓展任务，实现了中国首次平动点飞行，探测器于2012年4月离开平动点飞越探测4179小行星，在国际上首次获取该小行星的近距离光学图像。2014年10月，中国成功实施嫦娥5T1地月平动点拓展飞行，实现了继美国ARTEMIS任务后唯一的地月平动点验证飞行任务，尤其为2018年嫦娥四号的鹊桥地月平动点中继通信卫星奠定了坚实技术基础，这些任务为CE-5平动点拓展任务轨道设计提供了有益参考和借鉴。

与返回器分离以后，CE-5轨道器进入地心大椭圆轨道，因此，拓展任务的轨道类型主要为日地或地月平动点轨道和沿地心大椭圆前往平动点的转移轨道。

2.1 平动点轨道设计

平动点附近的动力学混沌特性明显，L1/L2点附近的典型轨道类型有Lissajous轨道和周期性的Lyapunov轨道、Halo轨道、垂直周期轨道、轴向周期轨道等。

平动点轨道设计方法包括解析方法和数值方法，前者采用如林兹泰德-庞加莱方法构造高阶解析解，作为实际轨道的近似解，后者采用如微分修正方法或多级微分修正方法等数值方法逼近实际轨道。相比较而言，前者需要理论推导和构建高阶解析公式，难以对光压摄动等非保守力建模，后者则难以获取状态连续的多圈轨道。由于CE-5拓展任务的目标平动点轨道选择Lissajous轨道、Lyapunov和NRHO轨道，且设计阶段仅需获取1～2圈精确的平动点轨道即可，因而采用数值法设计平动点轨道。

设平动点轨道在初始时刻和终端时刻的状态依次为和

(6)

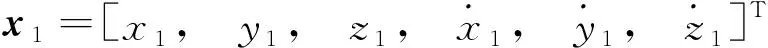
(7)

修正和飞行时间，使得达到期望值，即

(8)

式中:(,)为平动点轨道由至的状态转移矩阵。

平动点轨道设计时，一般使用CR3BP模型下的平动点轨道解作为初值，甚至直接使用线性解,即式(3)，然后在精确力模型下积分轨道，采取多次穿越平面的方式,利用式(8)修正初始状态，最终获取1～2圈精确的平动点轨道。

2.2 平动点转移轨道设计

目前平动点轨道的转移轨道设计主要基于不变流形方法，以达到节省能量的目的。不过，该方法需要计算平动点轨道流形，整体计算量较大。同时，由于拓展任务的初始轨道受主任务约束，运动状态可调整范围较小，若按照流形转移轨道设计思路，则修正计算难度较大。为此，基于嫦娥二号和嫦娥5T1平动点拓展任务设计经验，采取收敛性良好且计算量较小的平动点轨道直接转移与入轨方法，即修正轨道器的初始速度使之飞往目标平动点，同时得到相应的目标平动点轨道。

对于飞行时间较长的平动点转移轨道，直接利用微分改进方法有时难以收敛。或者，由于初始轨道历元和运动状态限制，无法通过仅调整初始速度实现自然转移并进入目标平动点轨道，此时必须增加轨道机动才可实现转移，以地月平动点轨道转移为例，如图2所示。

图2中，探测器离开地球前往日地平动点，一般可通过调整初始速度实现由日地平动点附近转移至地月平动点附近。若初始轨道历元和轨道参数偏差较大，仅调整初始速度可能无法实现转移，或者到达地月平动点轨道时需要很大的控制量才可进入平动点轨道，此时需要在转移过程中施加轨道机动，以确保探测器可以转移并进入地月平动点轨道，且总速度增量满足约束。

图2 施加中途轨道机动的平动点转移轨道Fig.2 Transfer trajectory with a mid-course maneuver to a libration point orbit

由此，平动点转移轨道设计的关键在于多个轨道机动时刻的选择问题，即选择合适的轨道机动时刻使得总转移能量最小，如图2中(,Δ)、(,Δ)和(,Δ)依次为初始转移轨道修正、中途轨道机动、平动点轨道机动的时刻和速度增量，即在给定时间约束范围内采用最优化方法求解使总速度增量Δ最优

(9)

3 拓展任务轨道设计结果

以与返回器分离后的CE-5轨道器轨道作为初始状态，设计平动点拓展任务，目标平动点轨道分别为日地Lissajous轨道、地月Lyapunov轨道和地月NRHO轨道。

3.1 日地Lissajous轨道

CE-5轨道器与返回器分离后，近地点高度较低，为了不影响返回器安全和挽救轨道器，需在分离后尽快施加规避机动抬升轨道器近地点高度。以近地点高度抬升至135 km为例，轨道器将进入周期约17.8天的地心大椭圆轨道，如图3中轨道“GDQ”所示。

进一步分析轨道器初始状态可知，若控制其逃逸地月空间则直接飞往日地L1点，因而选择日地L1点Lissajous轨道作为目标轨道。基于2.2节平动点转移轨道设计方法，采用精确力模型设计轨道器前往日地L1点的转移轨道，同时得到相应Lissajous轨道，如图3中轨道“SEL-1”所示，其中考虑地面测控需求，在近地点后10 h施加轨道机动，即图中▲所示，下文各图中的轨道机动位置均用此符号标记。

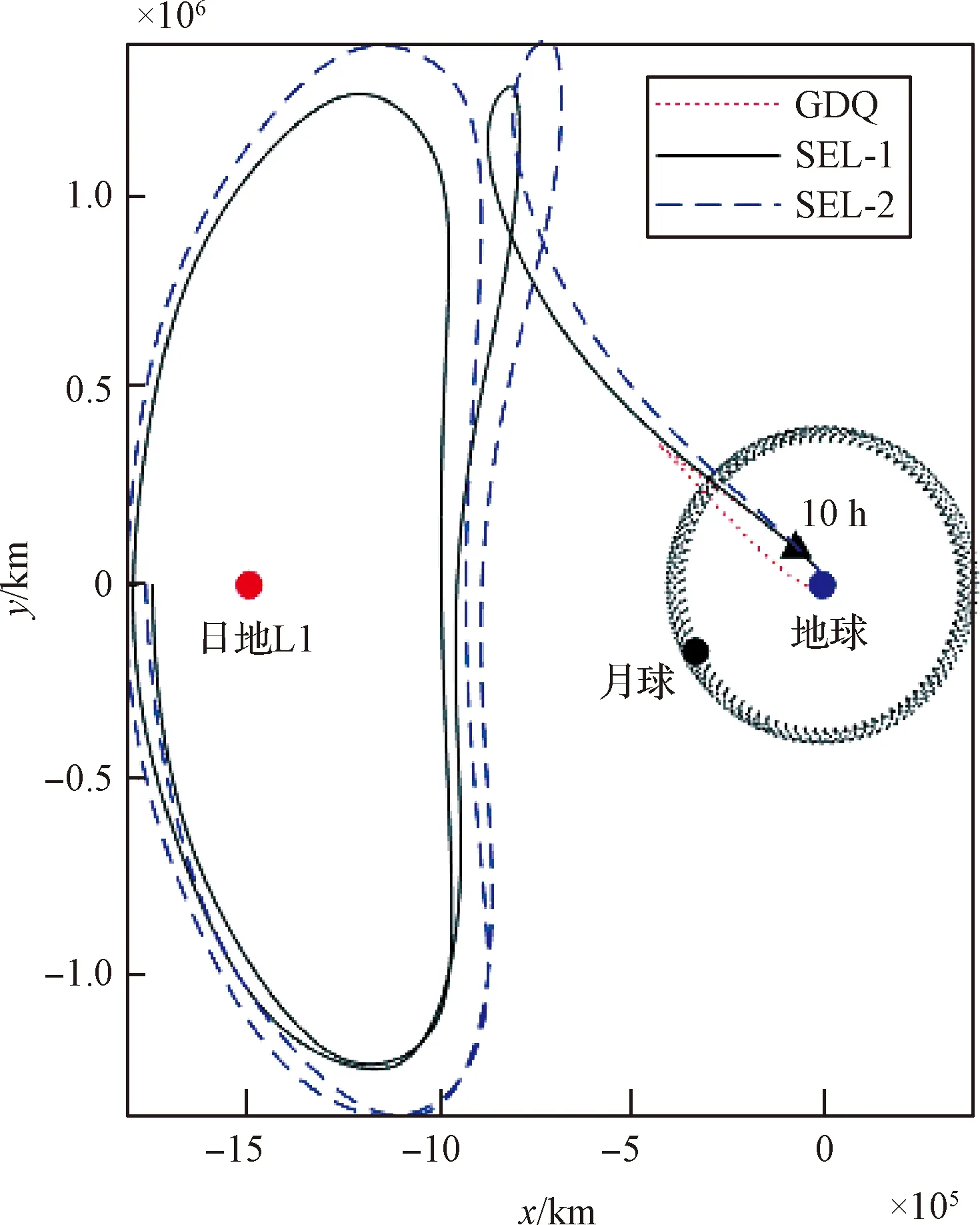
图3 CE-5轨道器日地Lissajous轨道拓展方案Fig.3 Scheme of Sun-Earth Lissajous orbit for the extended mission of CE-5 orbiter

作为对比给出轨道器近地点高度抬升至160 km，前往日地L1点的转移轨道及其Lissajous轨道，如图3中轨道“SEL-2”所示，图中日地Lissajous轨道绕日地L1点飞行1～2圈，可以根据实际任务需求延长飞行时间，平动点环绕飞行期间的轨道维持能量每年可优于10 m/s。

CE-5轨道器日地Lissajous轨道方案参数见表1，其中SEL-1的“轨道机动时机”为2次，依次为规避机动和近地点后10 h，SEL-2仅利用规避机动，事实上SEL-1也可以仅利用规避机动转移至日地L1点并进入Lissajous轨道，其速度增量即表中第三行给出的103 m/s。表1中的转移飞行时间为轨道器从近地点转移至日地L1点附近的平面所需时间。

2001年发射的日地L1点任务Genesis，在国际上首次采用了基于不变流形理论设计的低能量转移轨道，由地球发射至进入Halo轨道的转移时间约83天，表1中两个方案的飞行时间和转移轨道均与之接近，由此可见相应转移能量接近最优。

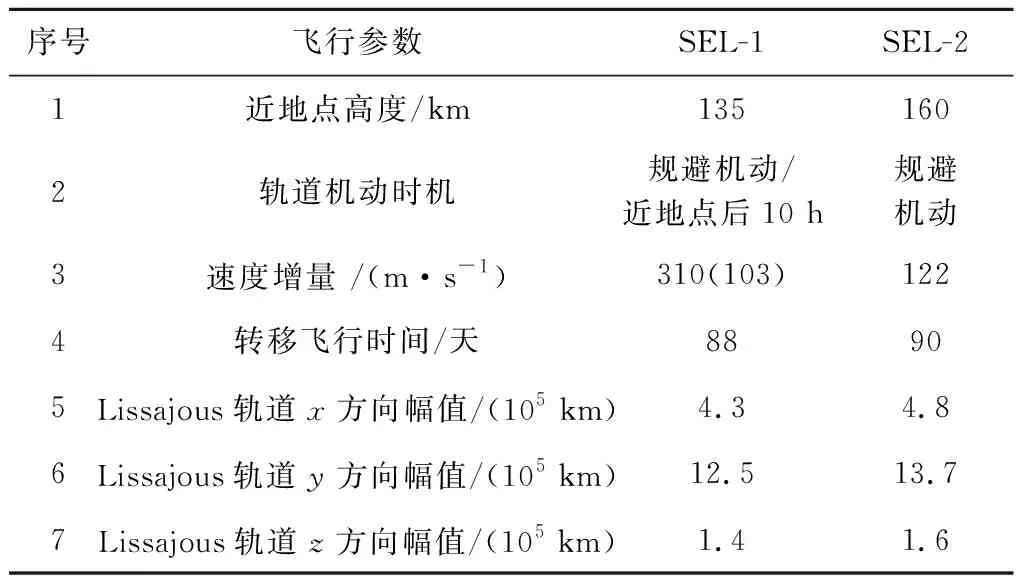
表1 CE-5轨道器日地Lissajous轨道方案参数Table 1 Scheme parameters of Sun-Earth Lissajous orbit for CE-5 orbiter

日地Lissajous拓展方案既可以实现对日地L1点的探测飞行，又可以为后续任务的规划、决策和实施提供时间缓冲，例如后续根据任务状态进一步开展日地L2点探测、地月空间探测、返回再入地球、地外天体探测等。

3.2 地月Lyapunov轨道

Lyapunov轨道是平动点动力学研究和任务设计的基础，目前尚未应用于实际任务，因此设计CE-5轨道器开展地月Lyapunov轨道验证飞行。

以前述近地点高度抬升至135 km的轨道作为初始轨道，设计轨道器前往地月Lyapunov轨道的飞行任务。借助月球近旁转向的方式，首先控制轨道器飞经1.5圈地心大椭圆轨道后与月球交会，期间包括规避机动控制和远地点轨道机动，飞行轨迹如图4(a)所示。然后，在近月点施加减速控制，轨道器前往地月L2点并自然进入Lyapunov轨道，在L2点绕飞半圈后进行轨道机动，轨道器将沿近似流形转移轨道逐渐离开地月L2点Lyapunov轨道，向地月L1点转移，期间将绕月球飞行1圈，截至环绕月球半圈的飞行轨迹如图4(b)所示。轨道器环绕月球1圈后转移至地月L1点并自然进入Lyapunov轨道，飞行轨迹如图4(c)所示。

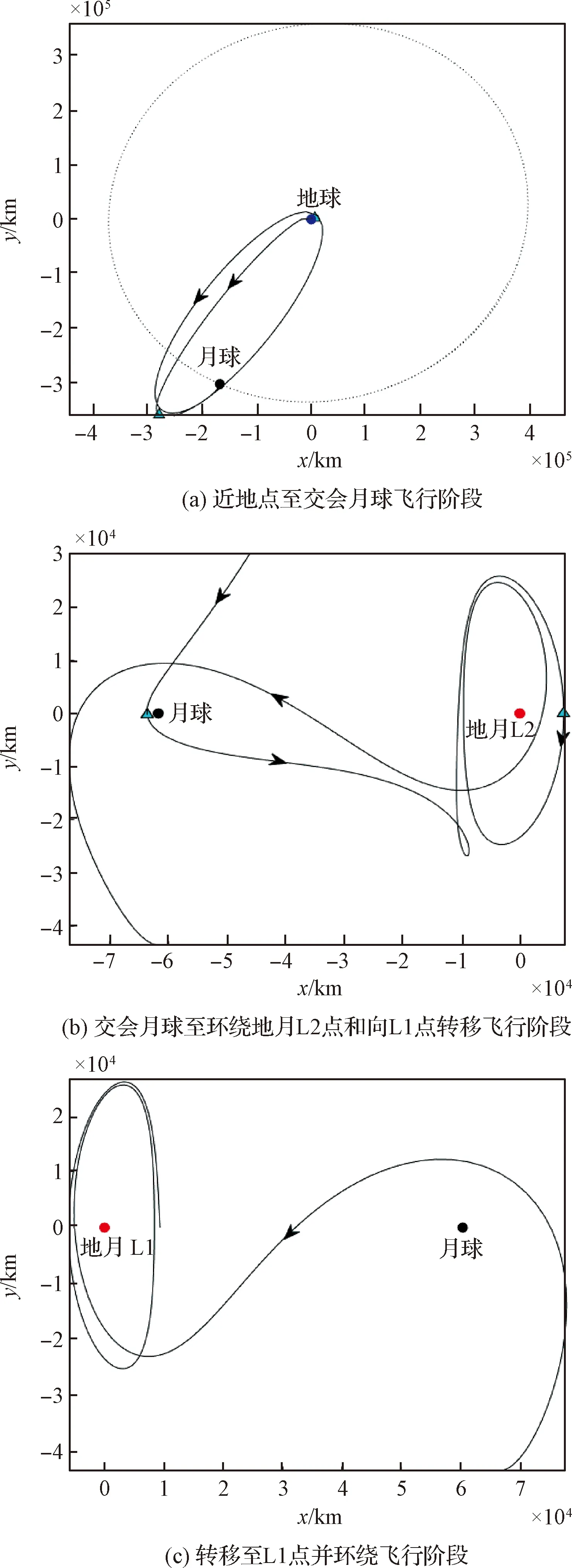
图4 CE-5轨道器地月Lyapunov轨道拓展方案Fig.4 Scheme of Earth-Moon Lyapunov orbit for the extended mission of CE-5 orbiter

CE-5轨道器地月Lyapunov轨道方案的飞行参数见表2。

表2 CE-5轨道器地月Lyapunov轨道方案参数Table 2 Scheme parameters of Earth-Moon Lyapunov orbit for CE-5 orbiter

该方案中地月Lyapunov轨道绕L1/L2点飞行1～2圈，可以根据实际任务需求延长飞行时间，平动点环绕飞行期间的轨道维持能量每年可以优于15 m/s。在地月Lyapunov轨道飞行后可以规划再拓展任务，如撞击月球终结使命、转移至地月和日地平动点开展探测、逃逸地月空间进入深空等。

该方案中由地球转移至近月点的飞行时间约10天，在近月点施加速度增量约259 m/s的控制后轨道器进入地月L2点Lyapunov轨道。文献[29]给出了前往地月L2点Lyapunov轨道的类似转移方式，根据目标轨道幅值不同所需的速度增量约220～540 m/s，但是仅考虑了CR3BP力模型。

3.3 地月NRHO轨道

NRHO轨道是距离月球较近的Halo轨道，是未来月球和深空探测空间站布设的首选轨道，目前美国“深空门户”空间站即采用NRHO轨道。

以近地点高度抬升至135 km的轨道作为初始轨道，设计轨道器前往地月NRHO轨道的拓展任务。考虑能量和飞行时间要求，给出2个轨道方案，其一为结合日地L1点探测飞行的地月NRHO轨道转移方案，即轨道器由近地点直接飞向日地L1点Lissajous轨道，进而转移返回地月系，进入地月NRHO轨道；其二为轨道器由近地点直接经深空机动返回地月系，然后进入地月NRHO轨道，二者对应的转移轨道和NRHO轨道分别如图5中的NRHO1和NRHO2所示。

图5 CE-5轨道器地月NRHO轨道拓展方案Fig.5 Scheme of Earth-Moon NRHO orbit for the extended mission of CE-5 orbiter

Folta计算了日地L2拟Halo轨道向地月L2点NRHO轨道的转移轨道，所需速度增量约128.5 m/s，转移时间约142天。与之相比，NRHO1方案由日地L1点转移至NRHO的总速度增量约288 m/s，但是转移时间仅85天;NRHO2方案由深空机动至NRHO的总速度增量约263 m/s，但是飞行时间仅为34.4天。因此，虽然本方案的能量消耗相对较大，但是却大大降低了作为空间任务尤其是拓展任务重要因素的飞行时间。

CE-5轨道器地月NRHO轨道方案的飞行参数见表3。

表3 CE-5轨道器地月NRHO轨道方案参数Table 3 Scheme parameters of Earth-Moon NRHO orbit for CE-5 orbiter

由表3可见，2个方案的NRHO轨道较为接近，其中转移飞行时间和能量可以根据实际任务需要做进一步优化。由于NRHO轨道的稳定性较好，可以在该轨道上做长期验证飞行，每年的轨道维持能量可以优于10 m/s，同时由于NRHO轨道的近月点较低，拓展任务结束后以较小能量即可实现撞月以终结使命，也可以较小能量返回地球或者前往深空。

4 结 论

文章研究了利用嫦娥五号轨道器的平动点拓展任务飞行方案，设计了包括日地Lissajous轨道、地月Lyapunov轨道和NRHO轨道在内的平动点轨道及其转移轨道，研究结果表明文中轨道动力学模型和轨道设计方法可以满足拓展任务设计需求，各方案所需速度增量不超过400 m/s，最小为103 m/s，转移至目标平动点轨道的飞行时间不超过90天，最短为70天。此外，若在轨道器规避机动时考虑后续拓展飞行，可有效节省轨道控制所需能量，因此实际任务设计时应综合考虑拓展任务需求，以实现任务资源的整体最优利用。